粗糙認知圖RCM模型研究

張春英，劉璐，歐陽東

(1.河北聯合大學 理學院，河北唐山 063009;2.河北聯合大學輕工學院，河北唐山 063009)

0 引言

認知圖(cognitive map，CM)［1］是表示和推理系統(tǒng)中概念間因果關系的圖模型。Kosko在1986年在Axelord認知圖概念間的因果關系中引入模糊測度，提出了模糊認知圖(fuzzy cognitive map，FCM)［3］，用于概念間模糊因果關系的表達與推理。我國學者駱祥峰［5］在2003年首次在概念間的因果關系中引入條件概率測度，提出概率模糊認知圖模型，該模型具有簡單、魯棒性好、實用等特點，具有比FCM模型對現實世界更為真實的模擬能力。然而，模糊認知圖和概率模糊認知圖僅從單個方面考慮，認為概念間的關系是唯一的，并且常常用一個固定的由專家主觀確定的模糊測度來反映。但是現實中，兩概念間的關系往往是多種多樣的，并且具有相應的屬性，因此用以表示概念間關系的邊會有多條，每條邊具有不盡相同的屬性權值，且權值隨著時間的變化、事件的發(fā)展而不斷變化。而在分析問題時，這些概念間的關系類的劃分是隨著人們的認識能力及具體要求的改變而改變的，這就涉及知識的分類及問題的表示，屬于不確定性問題中的粗糙問題。故此，本文將粗糙集［6］的思想融入到認知圖中，提出粗糙認知圖(Rough Cognitive Map，RCM)模型，粗糙認知圖可以將認知圖當中邊粗糙問題合理的轉化并解決，抽象出兩概念間的一個綜合關系，賦予權值，以完成認知圖的關系推理過程，并進行應用研究。

1 基本概念

1.1 認知圖及模糊認知圖

認知圖是一種以圖形的描述形式表示復雜系統(tǒng)模型的因果關系的方法。它用節(jié)點和邊分別表示概念(concept)及概念間的因果關系(relations of concept)，是表示和推理系統(tǒng)中概念間因果關系的圖模型。

認知圖的定義為:

定義 一個基本CM的拓撲結構是一個三元序組U=(V，E，W)，其中V={v1，v2，...vn}表示CM的概念節(jié)點集合，E={＜vi，vj＞|vi，vj∈V}是所有節(jié)點間的因果關聯有向弧。有向弧＜vi，vj＞表示節(jié)點vi對vj有因果關聯或影響)，W={wij|wij是有向弧＜vi，vj＞的權值}(即wij表示結點ci對cj的關聯或影響強度)。每個節(jié)點有一個狀態(tài)空間，(t)表示節(jié)點ci在t時刻的狀態(tài)值，(t)∈［－1，1］，其狀態(tài)值越大表示該概念的狀態(tài)越活躍。節(jié)點間有向連接弧對應的權值wij∈－1，0，{ }1 ，表示概念間關系增加與減少兩種定性狀態(tài)。

模糊認知圖［3，4，7］把概念間的三值{－1，0，1}邏輯關系擴展為區(qū)間［－1，1］上的模糊關系。其概念值為模糊值，也可以為二值，反映該節(jié)點對某概念以某種程度發(fā)生或表示概念狀態(tài)是關還是開。概念間的因果關系是模糊關系，其聯系強度也為模糊值。概念節(jié)點的輸出與兩種類型水平有關，即概念節(jié)點自身的狀態(tài)水平與外部因果聯系的強度。通過整個網絡中各概念節(jié)點的相互作用來模擬系統(tǒng)行為，是一種無監(jiān)督模型(unsupervised models)。

FCM推理的數學模型為:

式中Vci(t)為原因概念結點ci在t時刻的狀態(tài)值，Vcj(t)為結果概念結點cj在t+1時刻的狀態(tài)值，w為與cj有鄰接關系的概念結點集合，f為閾值函數(threshold function)，可以是二值的、S型的、模糊集合或概率函數。

1.2 粗糙集理論

設U是非空有限論域，R是U上的二元等價關系，R稱不可分辨關系，序對A=U，()R稱為近似空間。U/R是U上由R生成的等價類全體，它構成了U的一個劃分。U上的一族劃分稱為關于U的一個知識庫(knowledge base).令X?U，R為U上的一個等價關系。當X能表達成某些R基本范疇的并時，稱X是R可定義的，否則，稱X是R不可定義的。R可定義集也稱為R精確集，而R不可定義集稱為R粗糙集［6］(Rough Set)。

令知識庫K=U，()R，集合X?U，R是一個等價關系:

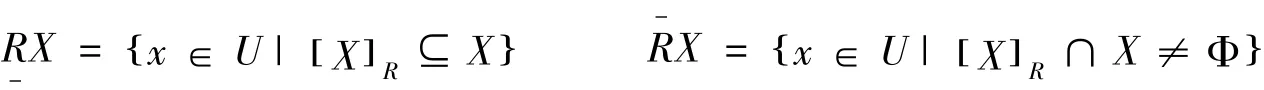
由等價關系R定義的集合X的近似精度如下:

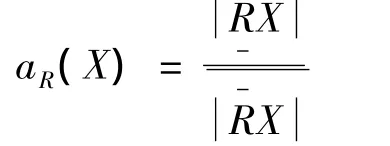
粗糙集是刻畫不確定性問題的一種手段，它在數據庫知識發(fā)現、數據挖掘等領域都得到廣泛的發(fā)展。它的特點是:無需借助于數據以外的先驗信息就可對數據進行比較客觀的處理。因此用粗糙集的思想能更客觀的分析系統(tǒng)，具有較深刻的意義。

2 粗糙認知圖

2.1 粗糙認知圖定義

定義2 給定集合G={e1，e2，…em} ，頂點集V={v1，v2，…vn}。若賦予頂點屬性后的邊組成集合E=∪ek＜vi，vj＞，則稱E是G的邊集。稱G=(V，E)是圖，其中=m分別為頂點和邊的個數。

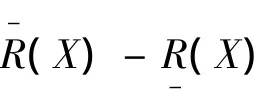
2.2 粗糙認知圖概念間權重的確定

邊精度aR(T)用來反映人們對粗糙圖T邊集知識了解的完全程度。

由上述粗糙認知圖的定義可知，兩概念間存在有限多條邊，并每條邊都具有屬性權值，基于認知圖的應用，我們必須抽象出兩概念間的一個綜合關系，并賦予權值，以完成因果關系推理，基于此，我們給定:

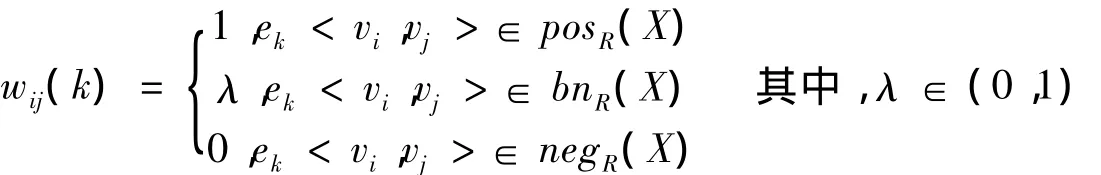
通過邊界域與上下近似之間的關系，經整理得:ρij=λ+(1－λ)aR(T)

3 粗糙認知圖模型

3.1 粗糙認知圖時間模型(Rough Cognitive Map Time Model，RCMTM)

認知圖及模糊認知圖理論參見文獻［7～14］。從這些文獻可以看出，雖然FCM具有較多的優(yōu)點，但它不能表示概念間的多種關系及關系測度對概念狀態(tài)值的動態(tài)依賴關系，也不能表示概念間因果關系測度的不確定性。如圖1所示，概念1與概念2之間的關系是多種多樣的，概念自身的狀態(tài)在變化，概念間的關系也是變化的。因此，其影響結果和程度肯定也會不同，從模糊認知圖的角度出發(fā)考慮概念間的關系是不符合分析實際的。

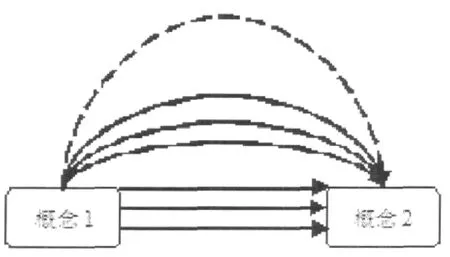
圖1

Eugene等證明了若在環(huán)中加入時間的方向性，則環(huán)中各概念就不會出現相互依賴關系［15］。Stylios等在Kosko的模糊認知圖模型中引入時間變量，為粗糙認知圖奠定了理論基礎［12～14］。

Stylios提出的具有時間及記憶狀態(tài)的FCM可以表示為:

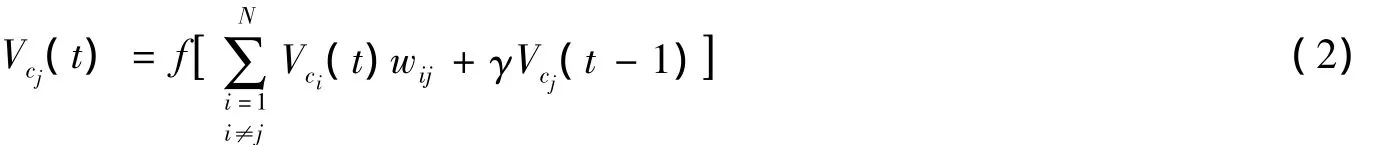
式中，Vcj(t)為概念cj在時間t的狀態(tài)值，γ為上一時刻狀態(tài)值對下一時刻時間狀態(tài)值的影響因子。

如果用近似精度ρij來代替式(2)中的wij，即得到我們提出的具有記憶功能與動態(tài)特性的粗糙認知圖時間模型(Rough Cognitive Map Time Model，RCMTM):

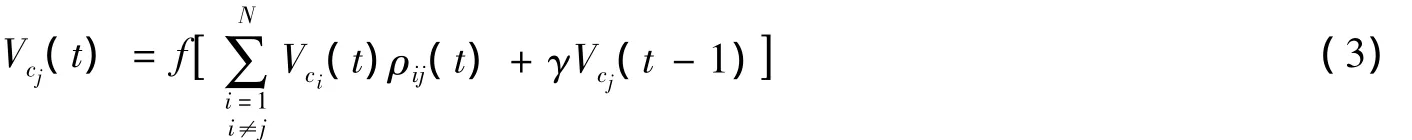
式中，隨著時間得變化，通過等價關系Rij劃分得到的等價類可能會發(fā)生變化，ρij隨之改變以反映兩概念間影響程度得大小。

對于圖1，用ρij可以很容易解決用FCM表示時存在的問題。由于在ρij中引入了時間項，ρij(t)不僅能表現出“概念1”與“概念2”間因果關系確定－不確定性，還能表現出這種因果關系的動態(tài)特性，并由不同關系集合X的確定，通過計算得出不同的ρij(t)值。因此，RCMTM不僅繼承了FCM的優(yōu)點，還自然擴展了FCM的應用領域及模擬概念間關系的能力。

3.2 粗糙認知圖時空模型(Rough Cognitive Map Space-Time Model，RCMSTM)

粗糙認知圖時間模型建立了一個隨時間變化的動態(tài)因果關系。實際上，概念間的關系除了會隨著時間變化而變化外，往往與空間上概念的狀態(tài)也是有關系的。如果我們在考慮因果關系時間特性的基礎上，進一步考慮因果關系的空間特性，則得到粗糙認知圖時空模型(Rough Cognitive Map Space－Time Model，RCMSTM)。其數學模型為:

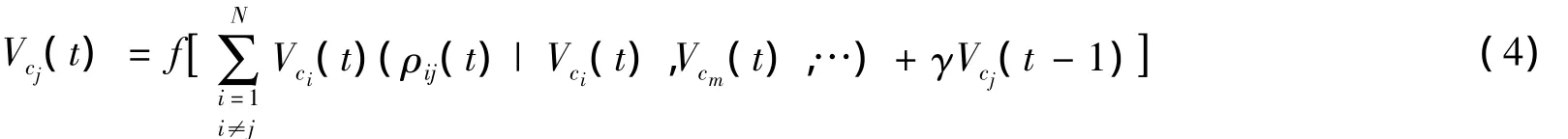
式(4)這種表達方法不僅解決了FCM存在的缺陷，使得認知圖不僅能處理概念間關系測度的不確定性，還對概念間因果關系的時空聯系加以有效的整合。如圖1中“概念1”對“概念2”的影響程度不僅與“概念1”的狀態(tài)有關，而且與“概念1”的積累狀態(tài)有關，表現為時間特性。同時影響程度還與空間上概念的狀態(tài)等有關，表現為空間特性。這樣就把關系測度的不確定性及聯系的時空特性有效的融入粗糙認知圖中，進一步擴展了粗糙認知圖。

4 RCM的性質

定理2 (1)給定粗糙圖T，對任一屬性集R，都有0≤aR(T)≤1。

由以上定理可知，隨著人們對粗糙圖T邊集X的知識了解完全程度的不同，反映在圖中即為邊屬性集的豐富程度的不同，則邊精度也會不同，從而邊的綜合權重也不同。

設C，V分別表示RCM的所有概念及概念狀態(tài)值，R表示所有概念間具有直接因果關系的測度。

定理3(RCM概念間等價變換定理)

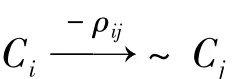
定理4 (RCM概念間動態(tài)測度等價關系定理)

在 RCM中若存在～Ci∈C，～Vi∈V，－ρij∈R，且ρij=λ+(1－λ)aR(T)，則－ρij(t)=1－ρij(t)。

上述兩個定理具有很重要的實際意義，它可從一個RCM得到一個新的RCM，能指導我們對一個新系統(tǒng)因果關系的認識，并能減少較多工作量。

5 結束語

本文介紹了認知圖模型和粗糙集的相關概念，為了克服認知圖和模糊認知圖的不足，本文提出了一種基于粗糙集理論的粗糙認知圖模型。具有以下三點貢獻:(1)肯定認知圖中兩概念間關系的多樣性，更好的模擬現實生活中存在的問題;(2)不僅能表現出概念間關系確定－不確定性，還能表現出關系的動態(tài)特性;(3)對概念間關系的時空聯系加以有效的整合;(4)針對認知圖和粗糙認知圖權值給定的主觀性這一缺陷，綜合邊精度客觀的給出兩概念間的綜合權重，使得粗糙認知圖與模糊認知圖相比計算量減小、復雜度降低。

關于粗糙認知圖的研究目前尚處于探索階段，還未形成相應的理論體系和系統(tǒng)的設計方法，存在許多的問題有待進一步研究與探索。

［1］Chaib-draa，B，J.desharnais.A relational model of cognitive maps［DB/OL］.http://citeseer.nj.nec.com/.2001，12.

［2］Axelrod R.Structure of Decision:the Cognitive Maps of Political Elites［M］.Princeton，NJ:Princeton University Press，1976.

［3］Kosko B.Fuzzy cognitive maps［J］.Int.J.Man-machine Studies，1986，24:65 ～75.

［4］Kosko B.Adaptive inference in fuzzy knowledge networks［C］.In:Proc.1st Int.Conf.Neural Networks，1987，2:261-26.

［5］駱祥峰，高雋.概率模糊認知圖［J］.中國科學技術大學學報.2003，33(1):26-33.

［6］張文修.粗糙集理論和方法［M］.科學出版社，2001.

［7］Liu Z Q，Miao Y.Fuzzy cognitive map and its causal inference［J］.In:Proc.IEEE Int.Conf.Fuzzy Systems Seoul Korea，1999，3:1540-1545.

［8］Bart Kosko.Fuzzy Engineering［M］.Prentice Hall，1997.

［9］Liu Zhi-qing，Satur R.Contextual fuzzy Cogni tivemap for decision support in geographic informati-on systems［J］.IEEE transactions on fuzzy systems，1999，5(10):495-502.

［10］Satur R，Liu Zhi-Qing.A contextual fuzzy cogni-tive map framework for geographic information sytems［J］.IEEE transactions on fuzzy systems，1999，7(10):481-494.

［11］Thierry Marchant.Theory and methodology cognitive maps and fuzzy implications［J］.EuropeanJourn-al of Operational Research ，1999，114:626-637.

［12］Liu Zhi-qiang，Miao Yuan.Fuzzy cognitive map and its causal inferences［C］.IEEE international fuzzy systems conference proceedings.KoreaSeoul 1999，22-25.

［13］Stylios C D，Groumpos P P.Fuzzy Cognitive maps:a soft computing technique for intelligent control［C］.Proc.2000 IEEE International Sym-posium on intelligent control Italy Patras:Ju-ly 17-19，2000.97-102.

［14］Groumpos.P.P Stylios.C.D，Modelling supervisor ycontrol systems using fuzzy cognitive maps［J］.Chaos Solitons and Fractals ，2000，11:329-336.

［15］Eugene Santor Jr.Probabilistic temporal networks:A unified framework for reasoning with time and uncertainty ［DB/OL］.http://citeseer.nj.nec.com/.2001，12.