設置RFPS系統的隔震結構水平震動響應分析

安軍海，趙巍，牛金鑫

(河北聯合大學河北省地震工程研究中心，河北唐山 063009)

0 引言

所謂基礎隔震，就是在基礎頂面和上部結構之間安裝一層具有足夠可靠性的隔震層，將基礎和上部結構隔離開來，有效控制地面運動向上部結構的傳遞［1-4］。由于隔震系統的水平剛度遠遠低于上部結構的抗側剛度，因此，可大大延長結構的自振周期，避開地震的卓越周期，使結構的變形和地震能量主要集中消耗在隔震層，而上部結構承擔的變形非常小。本文提到的RFPS隔震支座就是一種具有良好隔震效果的基礎隔震裝置，此支座是由上盤、下盤以及嵌套在它們之間的直徑較小的圓柱形輥軸(半徑R=0.2 m左右)連接而成。地震發生時，其滾動摩擦使一部分地震作用傳遞到上部結構，依靠滾動摩擦阻力的作用可以發生能量耗散，而依靠其上盤與上部結構的重力可以使結構復位。由于系統運動的動力反應特性的復雜性，有關這種隔震系統的研究工作還很少，本文根據多體動力學理論及達朗貝爾原理，建立了多自由度系統的計算模型并對其隔震效果進行分析計算。

1 RFPS系統滾動摩擦系數的確定

滑移摩擦是指兩個表面粗造的物體，當其接觸表面之間有相對滑動趨勢或相對滑動時彼此作用有阻礙相對滑動的阻力。其摩擦系數與接觸物體的材料和表面情況(如粗糙度、溫度和濕度等)有關，而與接觸面積的大小無關。然而，滾動摩擦則是當有外荷載沿法向作用在輥軸上時，摩擦副在接觸表面上不是在一個點上接觸，而是在一個半寬為a的長度上發生接觸，存在一個力偶矩的作用。因此，滾動摩擦在接觸界面上的運動學狀態與應力狀態與滑移摩擦是不同的，在確定滾動摩擦系數μr時，要用與滑移摩擦不同的模式來解釋滾動摩擦過程中所產生的能量消耗現象，根據現有的研究成果，滾動摩擦耗能起因主要有以下幾方面:

(1)微觀滑移引起的滾動阻力，包括:①自由滾動時，由于接觸雙方材料彈性常數不同引起的微觀滑移;②接觸表面同時存在切向力及法向力時的微觀滑移。

(2)材料非彈性變形引起的滾動阻力，包括:①彈性滯后的影響;②塑性變形的影響。

(3)粘付效應引起的滾動阻力。

(4)材料表面效應引起的滾動阻力。

總的滾動阻力為上述各因素引起的滾動阻力之和。不難看出，滾動摩擦是一種相當復雜的綜合作用過程，一般情況下，滾動摩擦系數μr大致取為一個百分之幾的數值［6］，為了簡化分析過程，暫時假定滾動摩擦系數在滑道上是一個在上述范圍之內的常數，大致估計RFPS輥軸摩擦擺的隔震效果。

2 Newmark－β方法簡介

對于有阻尼體系，可建立動力方程:

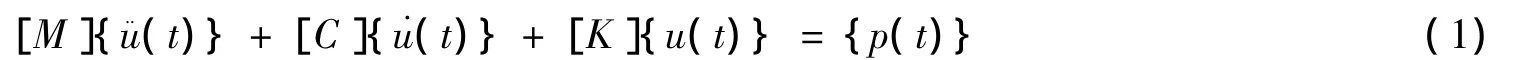
式中，［M］、［C］和［K］分別為n×n階質量、阻尼和剛度矩陣，及p(t{})分別為n階質點的運動加速度、速度、位移及節點荷載向量。

Newmark-β法是在線性加速度方法的基礎上提出的一種數值積分方法，它將時間離散化，運動方程僅要求在離散的時間點上滿足。

假定速度及位移可以用差分格式表示:

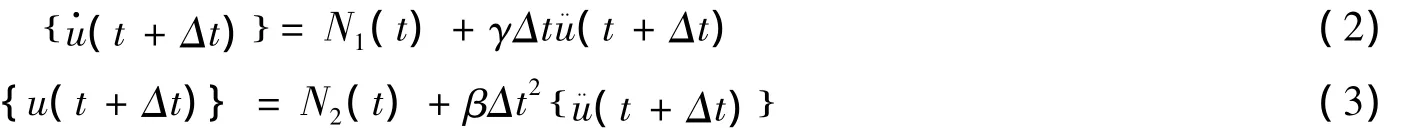
將式(2)和(3)代人式(1)可得:

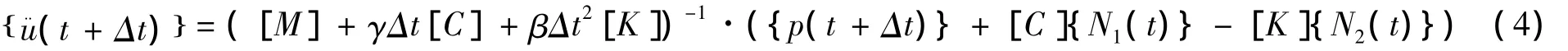
將式(4)代入式(2)、(3)即可得到t+Δt時刻的速度和位移向量。

Newmark－β法逐步積分格式為一積分格式群。其中，γ，β為精度控制參數。當γ，β滿足條件:γ≥1/2，β≥0.25(0.5+γ)2時，它為無條件穩定自起步格式;當γ=1/2時，計算精度為二階，否則，由于一些與“數值阻尼”及“周期延長”相關的誤差，其精度降為一階;γ=1/2，β=1/4時，退化為常平均加速度法;γ=1/2，β=1/6時，退化為線性加速度法;γ=1/2，β=1/8時，加速度為臺階形變化。

3 框架結構RFPS系統運動幾何關系分析

RFPS輥軸摩擦擺系統構靜力平衡位置造示意圖如圖1所示，實際結構工程中，為了保持結構的穩定與平衡，通常在水平和垂直方向設置多個支座，因此上盤只有平動而沒有轉動，但計算時可按一個支座考慮，且認為各個支座之間沒有相互影響。圖2給出了輥軸摩擦擺系統一般位置示意圖，圖2中，該系統的上盤與下盤弧面的半徑相同，均為R;r是輥軸的半徑;C、D分別是上盤弧面與下盤弧面的中心;O是輥軸橫截面圓心;T是輥軸在平衡位置時與圓弧滑道的接觸點;A是輥軸橫截面與上盤圓弧的接觸點;B是輥軸橫截面與下盤圓弧的接觸點;MN是通過O點的鉛錘線;設輥軸在t時刻的轉角是θ，取逆時針旋轉為正方向;輥軸截面圓心偏離平衡位置的角度為φ，則∠BOT=θ+φ;根據弧長BD=弧長BT，有(θ+φ)r=Rφ，因此:φ=θr/(R－r)。

圖1 平衡位置

圖2 輥軸摩擦擺系統一般位置示意圖

為了保證結構的正常復位，輥軸與滑道之間的接觸面應有足夠的滑動粗糙度，使二者之間不產生相對滑動。因此上盤的運動參數可由C點的運動參數代表。設輥軸截面在時刻t時的轉角是φ，上盤則根據幾何關系，得出上盤在x、y方向的位移x0、y0，速度，加速度，計算式如下:

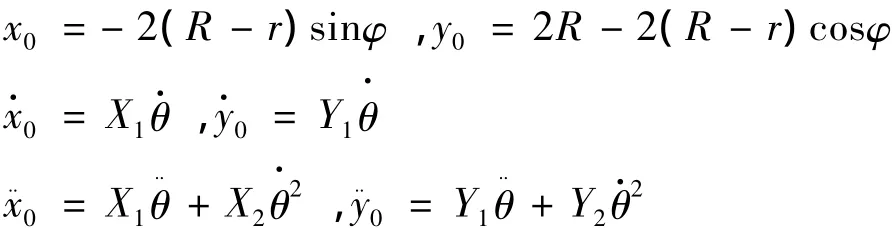
其中:

因此可以將θ看作是描述整個系統運動狀態的廣義坐標，即x0，y0及其各階導數都可以表示成廣義坐θ及其各階導數的函數。

4 RFPS輥軸摩擦擺系統運動方程

以設置RFPS輥軸摩擦擺六層框架結構為例來建立其運動方程，把每個樓層看作是一個質點，于是可將結構簡化成離散多自由度系統。其相應質量為mi，水平剛度與阻尼系數、豎向剛度與阻尼系數分別為kxi與cxi，kyi與cyi，六層框架結構的計算模型如圖3所示。

(1)接觸面上的法向反力與切向力的確定

由于輥軸的質量非常小，為了分析簡單，略去輥軸質量與截面轉動慣量的影響，設上盤的質量為m0，法向反力為N，切向力為F，由達朗貝爾原理，根據上盤在x方向及y方向的靜力平衡條件，可分別得:

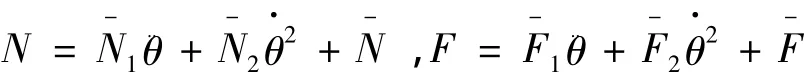
其中:

圖3 框架結構簡化模型

(2)RFPS系統運動方程的建立

利用動能定理建立系統運動方程。取上盤及輥軸作為一個獨立的隔離系統，則根據相對動能定理應有:

式中，dK表示系統在dt時間內的動能增量，表示形式為

(5)式中dW表示外力對系統所做的功，包括以下各項:

①系統中重力所做的功:dwg=-m0gy0dt，其中g是重力加速度;

②地震力所做的功:dwd，是地震地面加速度;

③彈性力與阻尼力做的功:

④輥軸在滾動過程中與上盤及下盤發生滾動摩擦作用產生功耗為ΔA，設滾動摩擦

系數為μr，根據滾動摩擦理論得:

式中系數2表示同時計入了在上盤與下盤發生的滾動阻力所做的功。

將以上各式代入到(5)式中，可以得到關于θ的運動方程:

其中:

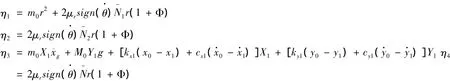
進而確定存在隔震系統時，質點m1至m6的運動方程分別為:

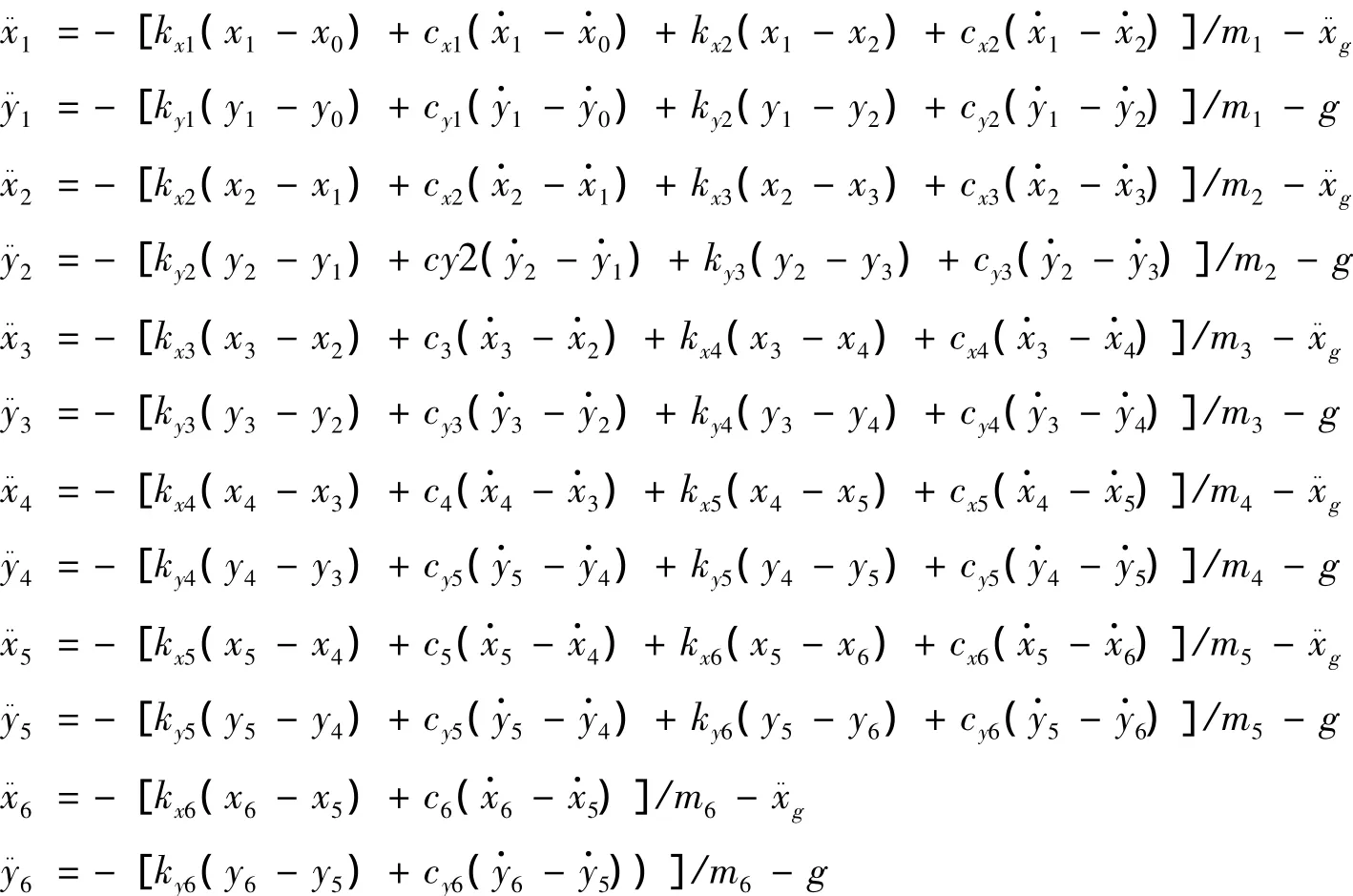
質點運動方程與(6)式構成非線性常微分方程組，可用Newmark－β數值積分方法求解。

當處于靜止狀態的輥軸有滾動趨勢時，由于滾動摩擦作用產生抵抗運動的阻力矩，當主動力矩大于或等于阻力矩時，輥軸才能開始滾動。因此，考慮在靜摩擦作用下，當結構處于停滯時段內，隔震系統不起作用，無需計算;而當結構處于非停滯時段內，隔震系統發揮作用，計算系統的地震動力反應。

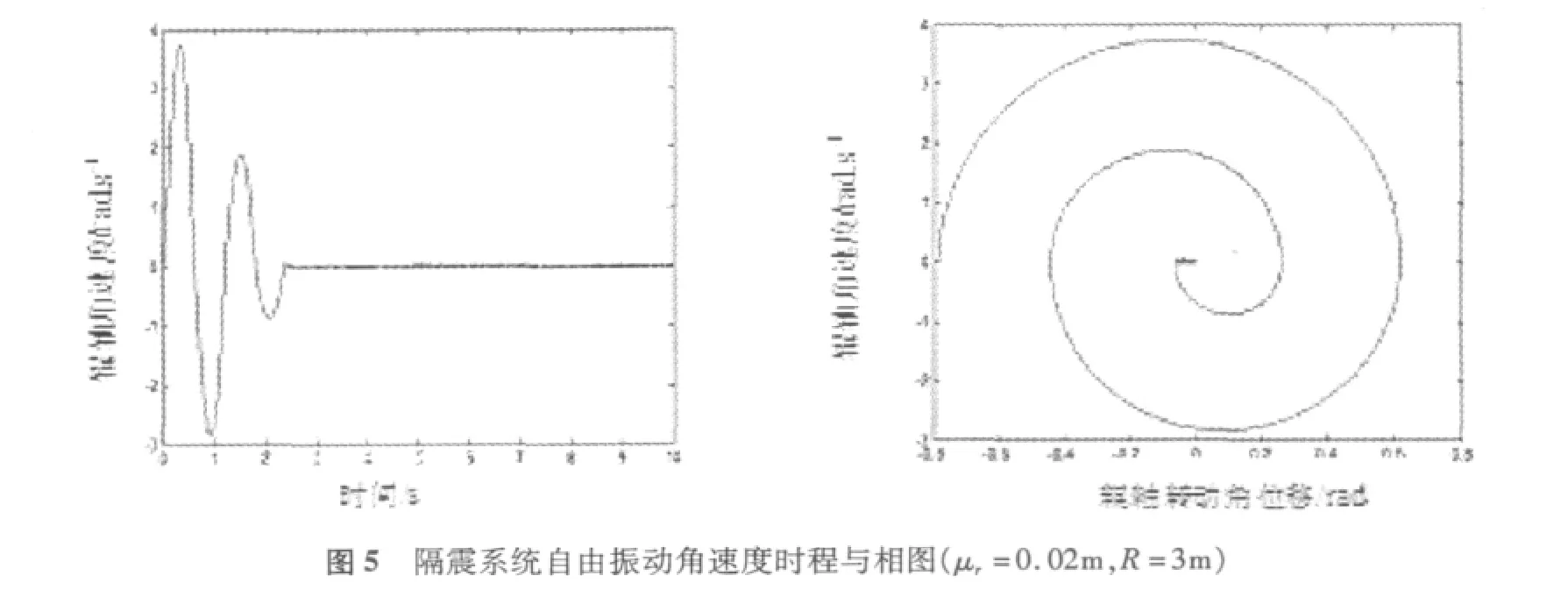
為考察RFPS系統的隔震、耗能及復位特性，將m1及其以上的質點除去，只考慮有上盤m0存在，暫時不考慮地面運動的影響，若給系統施加一個初始速度，則可以求得其自由振動動力反應時程及相平面跡線，分別如圖4及圖5所示。由圖4及圖5可見系統在滾動摩擦阻力的作用下振動幅度不斷衰減，最后達到靜止狀態。

5 結構的數值化計算與分析

為了更直觀地考察隔震系統的性能，現將六層框架結構簡化為六個多自由度體系，假設各層質量為mi=933t(i=1～6)，樓層之間抗側剛度和阻尼系數分別為ki=950000kN/m和ci=3000kN/(m.s)(i=1～6)。

運用Newmark－β方法，采用MATLAB編制求解軟件，輸入數值后得出滑道半徑對樓層位移、層間位移的影響以及滾動摩擦系數對層間位移的影響，如表1、表2和表3所示。

表1 滑道半徑對樓層位移的影響(mm)(r=20cm，μ=0.01)

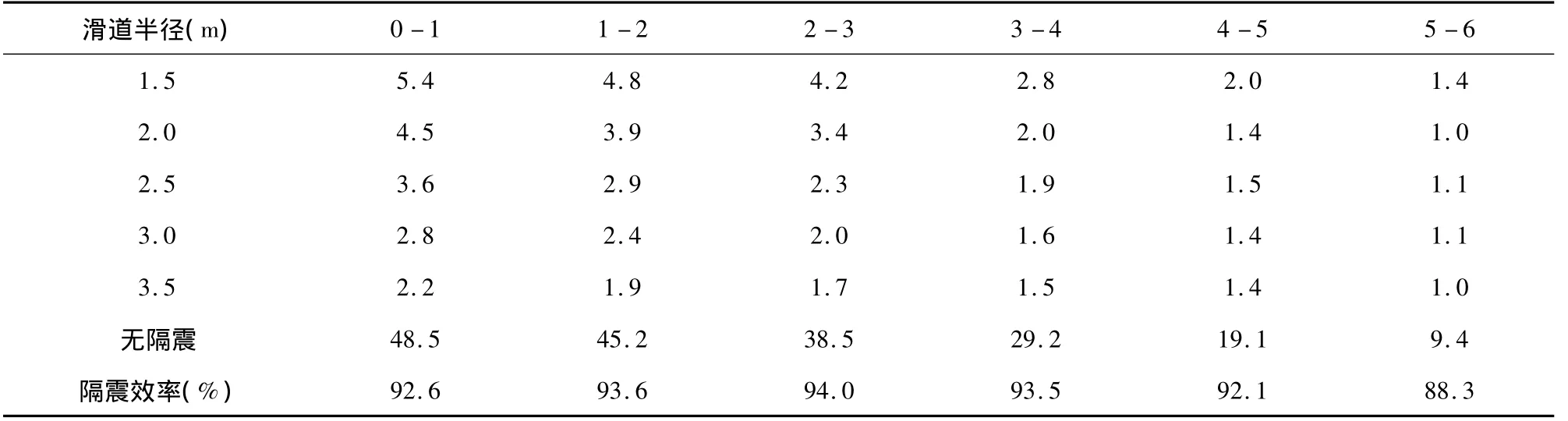
表2 滑道半徑對層間位移的影響(mm)(r=20cm，μ=0.01，R=2.5m)

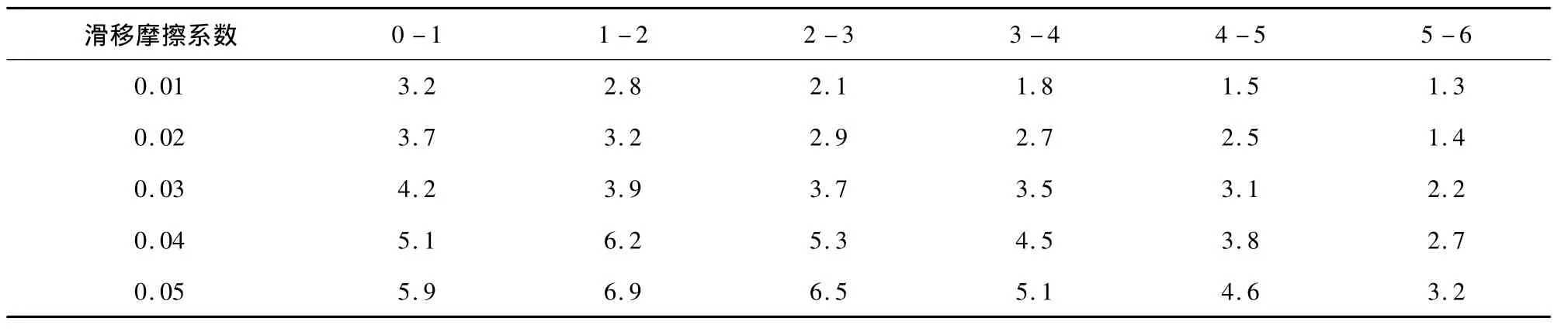
表3 滾動摩擦系數對層間位移的影響(mm)(R=2.5m，μ=0.01)

圖6和圖7給出了滑道半徑對樓層位移和層間位移的影響，圖8為滾動摩擦系數對層間位移的影響。

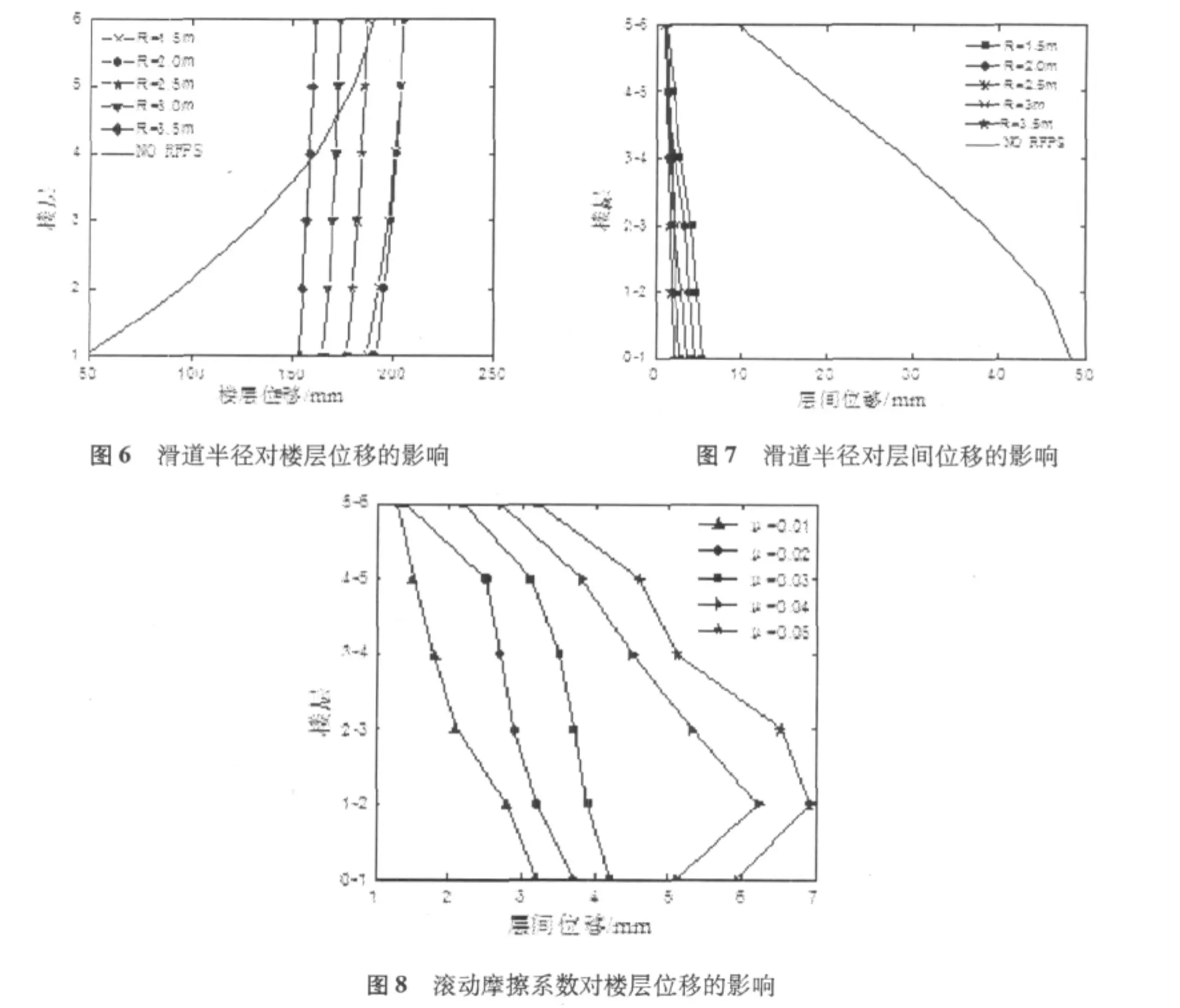
由圖6和圖7中可以看出，采用了滾動摩擦隔震系統之后，樓層位移有所增加但趨于均勻化，使樓層的層間位移值大幅減少，因此結構的內力、應變相應將會大幅降低。雖然結構的樓層位移有一定的增加，尤其第一、二層的位移增加較大，但它們都在合理的范圍之內。由圖7可以看出，輥軸的半徑尺寸對建筑物的層間位移的影響較小。圓弧滑道半徑越大，層間位移值也越小，二者呈單調的變化關系，但為了使結構有良好的復位性能而不宜使其半徑過大。由圖8可以看出，滾動摩擦系數越大，樓層層間位移也越大，這表明滾動摩擦可能也會產生對建筑物運動的阻滯作用。因此，滑道半徑和滾動摩擦系數都要視具體情況選取。

6 結論

(1)基于建筑物滾動摩擦隔震理論，建立了圓弧滑道輥軸摩擦隔震系統的運動微分方程及六層框架結構運動方程，用Newmark-β方法數值方法求解可以得到合理的計算結果;

(2)設置滾動摩擦隔震系統之后，上部結構的運動只保持平動而不發生轉動，無需在上盤設置轉向裝置，使其結構相對簡單。且依靠摩擦力偶的作用及上部結構自身阻尼，可以消耗傳入上部結構的地震能量。RFPS支座具有較好的復位能力與隔震效果;確定適當的圓弧滑道半徑與滾動摩擦系數值，隔震系統的隔震效率可以達到90%以上。

［1］Petros Komodromos.Seismic Isolation for Earthquake Resistant Structure［M］.Boston:WITpress Southampton，2000.

［2］周福霖.工程結構減震控制［M］.中國北京:地震出版社，1997.

［3］唐家祥，劉再華.建筑基礎隔震［M］.中國武漢:華中理工大學出版社，1993.

［4］武田壽一.構造物の免震防震制振［M］.東京:技報堂出版，1988.

［5］劉晶波，杜修力.結構動力學［M］.北京:機械工業出版社，2006.

［6］Johnson K L.Contact Mechanics［M］.London，Cambridge University Press，1985.

［7］Zayas V，Low S S，Mahin S A.A simple pendulum technique for achieving seismic isolation［J］.Earthquake Spectra，1990，6(2):317-331.

［8］李大望，周錫元，王東煒.摩擦擺系統振動性態的進一步分析［J］.振動工程學報，2001，14(3):330-333.

［9］Hwang J S，Evaluation of equivalent linear analysis methods of bridge isolation ［J］.Journal of structure engineering，ASCE，1996，122(8):972-976.

［10］Wang Yen-Po，Chung Lap-Loi，Liao，Wei Hsin.Sesmic response analysis of bridges isolated with friction pendulum bearings［J］.Earthquake Engineering ＆ Structural Dynamics，1998，27(10):1069-1093.

［11］葛楠，蘇幼坡，王興國.建筑物滾動摩擦隔震理論［J］.河北理工大學學報(自然科學版)，2008，30(4):132-136.