絕緣子人工污穢閃絡電壓變異系數的統計分析

王少華，黃曉明，劉黎，梅冰笑，殷明，胡軍，鄒曉峰

（1.浙江省電力試驗研究院，杭州310014；2.寧波電業局，浙江寧波315010）

輸配電技術

絕緣子人工污穢閃絡電壓變異系數的統計分析

王少華1，黃曉明2，劉黎1，梅冰笑1，殷明2，胡軍1，鄒曉峰1

（1.浙江省電力試驗研究院，杭州310014；2.寧波電業局，浙江寧波315010）

掌握絕緣子污閃試驗數據的分散性對于絕緣子選擇和設計具有重要意義。對同一污穢條件下、同一絕緣子污閃電壓的變異系數及置信上限進行了統計分析；對不同污穢條件下、不同絕緣子的污閃電壓變異系數的分布規律及統計量進行了分析。結果表明：采用均勻升壓法得到的絕緣子污閃電壓變異系數置信上限的最大值為0.130；采用均勻升壓法得到的絕緣子污穢閃絡電壓的變異系數近似服從正態分布，期望值為5.32%，其95%置信區間的上限為5.61%，與采用升降法得到的污穢閃絡電壓變異系數的期望值基本一致。

絕緣子；人工污穢；污閃電壓；變異系數；分散性；置信區間

0 引言

為掌握不同環境條件下各種結構型式絕緣子的污閃特性，為輸電線路外絕緣選擇和設計提供參考依據，國內外研究者開展了大量的試驗研究，獲得了大量的污閃試驗數據[1-6]。然而，實踐表明，同一絕緣子、在同一試驗室、采用同一試驗方法、由同一試驗人員在很短時間間隔內（可認為環境條件及絕緣狀況保持恒定）測得的閃絡電壓也有一定的分散性。若絕緣子尺寸、形狀和表面加工狀況不同（如金屬附件表面是否有毛刺、疙瘩），未能掌握影響污閃電壓試驗結果重復性和再現性的某些變化因素，其測量結果的分散性將更為明顯[7-8]。如何對不同工況下分散的污閃試驗數據進行統計分析，掌握污閃電壓試驗值的離散程度，對于絕緣子選擇和設計具有重要意義。

IEC 60815中采用統計方法（包括統計法和簡化統計法）選用絕緣子[9]，其前提條件也是掌握絕緣子污閃特性（絕緣子強度）的分散性。

統計學中，常采用標準差（standard deviation）和變異系數（variation coefficient）這2個統計量來表征資料的分散性，即觀測值的分散變異程度。其中，標準差是有量綱的，而變異系數則無量綱。當對2組或多組數據的變異程度進行比較時，如果度量單位與平均數相同，可以直接利用標準差來比較。當度量單位或平均數不同時，就不能采用標準差來比較，而需采用其它統計量。對于絕緣子污閃試驗，不同試驗條件、不同絕緣子的污閃電壓均值也是不同的。因此，不能簡單地利用標準差來比較不同試驗條件、不同絕緣子的污閃電壓離散程度差異，而需要采用變異系數作為統計量。很多文獻在污閃數據處理分析時計算變異系數，以說明污閃電壓的有效性[10-15]，但并未對變異系數這一統計量做統計分析。

當采用均勻升壓法進行污閃試驗時，為獲得同一污穢條件下、同一絕緣子的污閃電壓，常需要進行多次有效試驗。本文首先對同一污穢條件下、同一絕緣子污閃電壓的變異系數及置信上限進行統計分析，再對不同污穢條件下、不同絕緣子的污閃電壓變異系數進行整體統計分析，驗證其正態分布規律，給出了期望值及95%置信區間，為絕緣子選擇的統計方法提供了理論基礎。

1 變異系數及其置信上限

目前，變異系數的統計推斷方法主要適用于正態隨機變量。設隨機變量X服從正態分布N（μ，σ2），其中，均值μ和方差σ2未知。假設X1，X2，…，Xn是X的一組樣本，樣本均值和方差分別記為和S2，則隨機變量服從自由度為n-1、參數為的非中心t分布，其中CV為隨機變量X的變異系數，即：

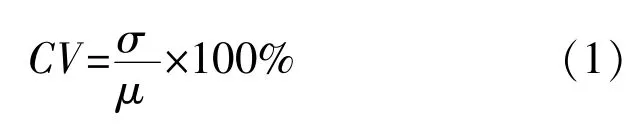
當獲得樣本X1，X2，…，Xn的觀測值x1，x2，…，xn及其均值和標準差s時，樣本變異系數cv可按下式計算：

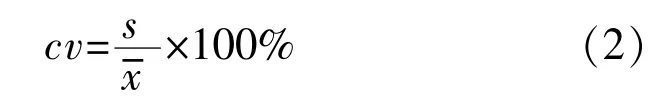
變異系數可以消除因度量單位或平均數不同而對2組或多組數據變異程度比較產生的影響。

由GB/T 10094-2009可知，正態總體變異系數CV的置信上限CVU的精確值可由下式確定[16]：

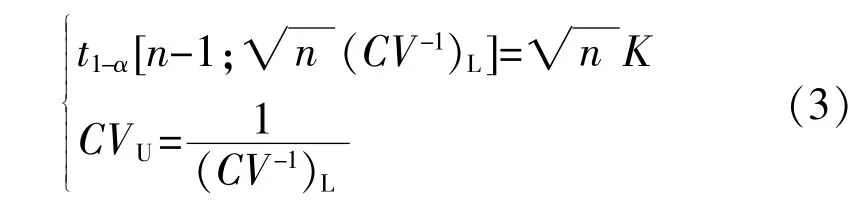
當CV＜0.30，n≥6時，正態總體變異系數CV置信上限CVU的近似值為[16]：

2 污閃電壓變異系數的計算結果

IEC 60507-1991推薦的絕緣子人工污穢試驗標準方法為鹽霧法和固體層法。然而，這兩種方法耗時很長，工作量很大。試驗研究中也常采用均勻升壓法。均勻升壓法是以一定的速度均勻升高試驗電壓，直至絕緣子閃絡。雖然這種方法與實際運行狀況不同，但能節省很多時間。而且，大量試驗結果也表明，由均勻升壓法得到的交流污閃電壓與升降法得到的基本一致，因此該方法得到了廣泛應用[19]。當采用均勻升壓法測量閃絡電壓時，根據式（2），可得絕緣子污閃電壓變異系數cv為：

式中：Uav為絕緣子的污閃電壓平均值；Ui為第i次試驗閃絡電壓；n為試驗次數。

文獻[15]給出了在實驗室采用均勻升壓法得到的多種結構型式絕緣子在不同鹽密、灰密條件下的污閃電壓平均值，共89組。根據式（5）計算得到的變異系數如表1所示。

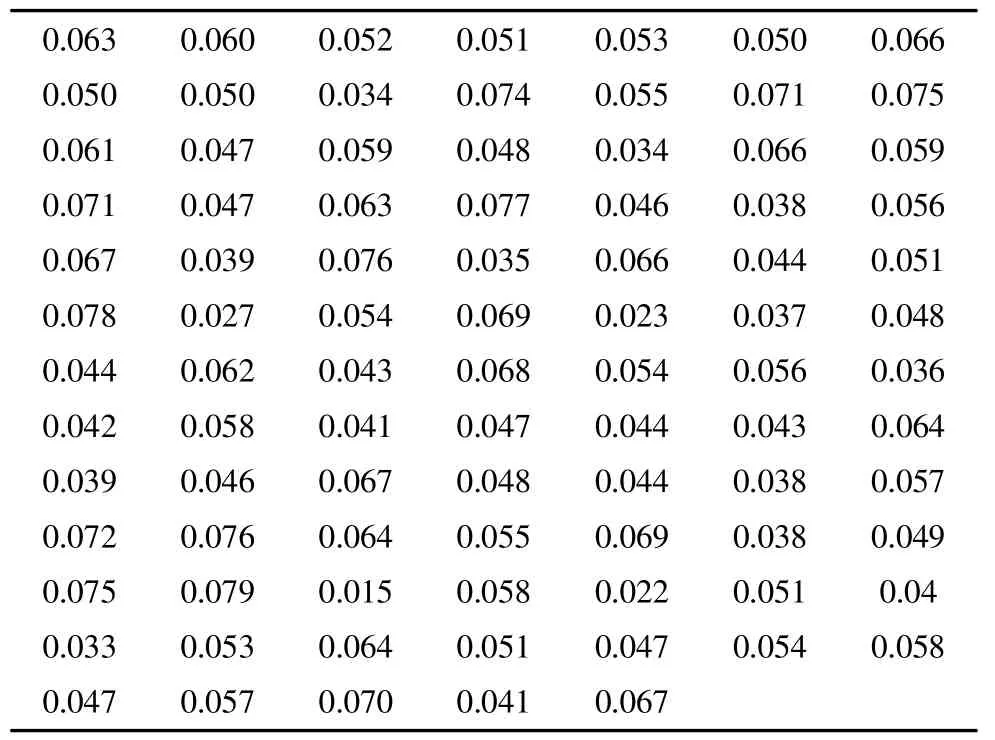
表1 絕緣子人工污穢閃絡電壓變異系數

由表1可知，絕緣子人工污穢閃絡電壓變異系數均小于0.30。由文獻[15]可知，為獲得有效的污閃電壓值，同一鹽密、灰密條件下的試驗次數n不少于10。因此，當置信水平為0.95時，根據式（4）可計算出與89個污閃電壓相對應的人工污穢閃絡電壓變異系數置信上限，見表2。

表2 絕緣子人工污穢閃絡電壓變異系數置信上限

由表2可知，采用均勻升壓法得到的絕緣子污閃電壓變異系數置信上限的最大值為0.130。

3 污閃電壓變異系數中的異常值判斷

由于試驗誤差的存在，有必要采用數理統計方法判斷并剔除污閃電壓變異系數中的異常數據。常用的方法有拉依達法、肖維納特（Chavenet）法、格拉布斯（Grubbs）法等[20]。本文采用格拉布斯法進行異常數據檢驗。

格拉布斯法的基本原理是：首先假定測量結果服從正態分布，根據順序統計量來確定可疑數據的取舍。為了檢驗樣本數據xi（i=1，2，…，n）中是否有可疑值，可將xi按其值由小到大順序重新排列，根據順序統計原則，給出格拉布斯統計量g。

當最小值x1可疑時：

當最大值xn可疑時：

根據格拉布斯統計量的分布，在指定的顯著性水平β（一般β=0.05）下，求得判別可疑值的格拉布斯檢驗臨界值g0（β，n）。格拉布斯法的判別標準為：當g≥g0（β，n），則判定與g對應的最小值x1（或最大值xn）為異常數據。

對于表1所示的絕緣子人工污穢閃絡電壓變異系數，異常值只可能為高端值，因此需要進行上側檢驗。計算結果如下：

由于g＜g0（0.05，89），因此可判斷表1所示污閃電壓變異系數中不存在異常數據。

4 污閃電壓變異系數的分布規律

中心極限定理表明：如果1個變量是由大量微小、獨立的隨機因素疊加而成，那么這個變量一定滿足正態分布。以表1中的89個污閃電壓變異系數為研究對象，對比污閃電壓變異系數頻數直方圖及正態分布的概率密度函數圖（如圖1所示），得到初步結論是污閃電壓的變異系數可能服從正態分布。

利用Matlab中的統計繪圖函數normplot（x）進行分布的正態性檢驗[21]，結果如圖2所示。經觀察，這89個離散點非常靠近傾斜直線段，圖形為線性，因此可得出污閃電壓變異系數近似服從正態分布N（μ，σ2）的結論。

圖1 帶正態密度函數的頻數直方圖

圖2 污閃電壓變異系數的正態假設檢驗

根據表1中數據，利用Matlab中的統計繪圖函數normfit（x）可計算得到：期望值μ=0.053 2，其95%置信區間為[0.050 3，0.056 1]；標準差σ= 0.013 9，其95%置信區間為[0.012 1，0.016 3]。

由文獻[8]可知，采用升降法得到的污穢閃絡電壓變異系數均值約為5%；而本文的統計分析結果表明，采用均勻升壓法得到的污穢閃絡電壓變異系數均值約為5.32%，二者基本一致。

5 結語

絕緣子污閃電壓試驗數據具有分散性，本文對不同污穢條件下、不同絕緣子的污閃電壓變異系數進行了統計分析。結果表明：采用均勻升壓法得到的絕緣子污穢閃絡電壓的變異系數近似服從正態分布，期望值為5.32%，其95%置信區間的上限為5.61%，與采用升降法得到的污穢閃絡電壓變異系數的期望值基本一致。

[1]范建斌，黃志秋，謝榮坤，等.直流輸電線路Y型絕緣子串污閃特性研究[J].電網技術，2007，31（18）:32-35.

[2]李震宇，崔吉峰，周遠翔，等.絕緣子安裝結構對污閃電壓的影響[J].電網技術，2005，29（16）:56-59.

[3]孫才新，司馬文霞，舒立春.大氣環境與電氣外絕緣[M].北京：中國電力出版社，2002.

[4]關志成.絕緣子及輸變電設備外絕緣[M].北京：清華大學出版社，2006.

[5]關志成，龍彪，張福增，等.高海拔地區直流絕緣子不同懸掛方式污閃特性[J].高電壓技術，2007，33（10）:1-5.

[6]王向朋，周軍，王黎明，等.高海拔下特高壓直流絕緣子的污閃特性[J].高電壓技術，2008，34（9）:1869-1874.

[7]邱志賢.高壓絕緣子的設計與應用[M].北京：中國電力出版社，2006.

[8]邱志賢.關于高壓絕緣子交流人工和自然污穢閃絡電壓的分散性[J].電瓷避雷器，2009（5）:1-4，8.

[9]IEC 60815-1986，Guide for the selection of insulators in respect of polluted conditions[S].

[10]苑吉河，蔣興良，張志勁，等.高海拔現場標準懸式絕緣子的交流污閃特性[J].電網技術，2009，33（5）:58-61.

[11]蔣興良，舒立春，張永記，等.人工污穢下鹽/灰密對普通懸式絕緣子串交流閃絡特性的影響[J].中國電機工程學報，2006，26（15）:24-28.

[12]蔣興良，陳愛軍，張志勁，等.鹽密和灰密對110 kV復合絕緣子閃絡電壓的影響[J].中國電機工程學報，2006，26（15）:150-154.

[13]舒立春，楊新春，蔣興良，等.低氣壓下絕緣子短波頭操作沖擊污閃特性[J].電網技術，2008，32（17）:94-97.

[14]胡建林，蔣興良，張志勁，等.布置方式對直流絕緣子串人工污穢閃絡特性的影響[J].電網技術，2006，30（23）: 15-18.

[15]苑吉河.輸電線路絕緣子（串）交流污閃特性及放電過程的研究[D].重慶：重慶大學，2008.

[16]GB/T 10094-2009正態分布分位數與變異系數的置信限[S].北京：中國標準出版社，2010.

[17]GB/T 15932-1995非中心t分布分位數表[S].北京：中國標準出版社，1996.

[18]GB/T 4086.2-1983統計分布數值表-χ2分布[S].北京：中國標準出版社，1984.

[19]蔣興良，舒立春，孫才新.電力系統污穢與覆冰絕緣[M].北京：中國電力出版社，2009.

[20]王秉鈞，談克雄.數理統計在高電壓技術中的應用[M].北京：水利電力出版社，1990.

[21]包研科.數理統計與精MATLAB數據處理版[M].遼寧：東北大學出版社，2008.

（本文編輯：龔皓）

Statistical Analysis on Variation Coefficient for Artificial Pollution Flashover Voltage of Insulators

WANG Shao-hua1，HUANG Xiao-ming2，LIU Li1，MEI Bing-xiao1，YIN Ming2，HU Jun1,ZOU Xiao-feng1

（1.Zhejiang Electric Power Test and Research Institute，Hangzhou 310014，China；2.Ningbo Electric Power Bureau，Ningbo Zhejiang 315010，China）

It is of great significance to master the data dispersity in the pollution flashover test of insulators. This paper performs the analysis on the variation coefficient of pollution flashover voltages for the same insulators and the upper confidence limit statistically under the same pollution conditions as well as the distribution rules and the statistics of variation coefficient of pollution flashover voltages for different insulators under different pollution conditions.The results show that the upper confidence limits，which are obtained with the step-up method，have a maximum of 0.130，and the variation coefficients have an approximate normal distribution with the mathematical expectation of 5.32%，and its upper confidence limit is 5.61%in 95%of confidence interval，which is consistent with the results obtained with up-and-down method.

insulator；artificial pollution；pollution flashover voltage；variation coefficient；dispersity；confidence interval

TM85

：A

：1007-1881（2012）02-0001-04

2011-10-11

王少華（1981-），男，安徽寧國人，博士，工程師，主要從事輸變電設備外絕緣技術研究工作。