基于希爾伯特-黃變換的復雜電能質量信號檢測技術

胡曉曦 劉含露 熊婷婷 胡京瑩

（1.長沙理工大學電氣與信息工程學院，長沙 410114；2.湖北咸寧市供電公司，湖北 咸寧 437100）

提供高可靠性、高質量的電能是智能電網建設的目標之一[1-2]。但是隨著智能電網的發展，各種非線性負荷也在不斷的增長，給供電系統電能質量造成嚴重的問題[3]；另外高智能的用電設備也對電能質量提出了更高的要求；這些電能質量問題越來越引起電力部門和電力用戶的高度重視，在國家電網公司發布的《智能電網關鍵設備（系統）研制規劃》中指出：要建設電能質量監測和治理裝置[4]。

目前，國內外提取電能質量擾動信號特征量的方法主要有傅里葉變換[5]、S變換[6]、小波變換[7]等。傅里葉變換只適合平穩信號分析，無法滿足對具有暫態、突變等特性的電能質量擾動的非平穩信號進行分析的要求[8]。小波變換中小波基對信號的小波變換結果影響很大。然而，目前如何選擇小波基還沒有統一的方法或可遵循的原則[9]。

HHT是近年來發展起來的一種信號分析的新方法[10]。它對處理非線性、非平穩信號有很明顯的有效性和優越性：它沒有固定的先驗基底，是完全自適應的；通過Hilbert變換得到的瞬時頻率具有清晰的物理意義，能夠表達信號的局部特征；可以準確地揭示數據的內部特征，在時頻域得到較高的分辨率，相較于其他方法可以有更好的結果。所以本文采用HHT(Hilbert-Huang Transform)變換法分別對單擾動和多擾動電能質量信號進行精確檢測。

1 HHT基本原理

HHT變換主要是由兩個部分構成：經驗模態分解（EMD）和Hilbert變換，其廣泛用于非線性非平穩信號的分析。

1.1 經驗模態分解

EMD是提取信號中的IMF分量，其方法如下：首先根據信號s(t)的極大點和極小點求出其上包絡線v1(t)及下包絡線v2(t)的平均值m1(t)，即

將原數據序列s(t)減去m1(t)可得到一個去掉低頻的新數據序列h1(t)：

重復處理以上過程k次，直到h1(t)得到的均值趨于零為止，這樣就得到了第1個IMF分量c1(t)，它代表信號s(t)中最高頻率的分量：

將c1(t)從s(t)中分離出來，可得到一個去掉高頻分量的差值信號r1(t)，即有

將r1(t)作為原始數據，重復循環以上步驟得到第二個IMF分量c2(t)，重復n次，直到使 rn(t)成為一個單調函數，循環終止，得到n個IMF分量。這樣就有

以上是 EMD分解，可以將不同頻率的信號分離出來。

1.2 希爾伯特變換（Hilbert）

對IMF進行希爾伯特變換就能得到信號的時頻圖，能夠準確找到信號突變發生的時間。設Y(t)是信號X(t)的希爾伯特變換,即

其中，P為柯西主值，它對于所有PL級函數都成立，通過這一定義，X(t)和Y(t)為復共軛對，即

可以得到解析信號Z(t)

式中，a(t)為瞬時幅值，θ(t)為相位。

瞬時頻率定義為：

EMD分解和與其相應的希爾伯特變換一起被稱為HHT變換。本方案用瞬時頻率 f(t)來定位信號的準確時間。

2 單擾動簡單信號的仿真及結果分析

電力系統中主要的電能質量問題是電壓暫降和諧波問題，本文先以電壓跌落和諧波單擾動狀態監測為例，做電壓暫降和諧波含有量HHT仿真驗證。

2.1 單擾動電壓暫降

在Matlab中產生標準工頻信號，在不同時刻加入階躍信號來產生電壓暫降現象，電壓暫降信號如圖1所示。

圖1 電壓擾動信號

電壓有效值為220V的某相線路發生電壓暫降，電壓暫降從發生到終止的理論時刻為 0.22s到0.63s，跌落幅度為 120V。HHT仿真得到時頻關系如圖2所示，時間幅度關系如圖3所示。

圖2 電壓擾動時頻關系

圖3 電壓擾動時間幅度關系

由圖2和圖3可以看出檢測出來的電壓暫降時間為0.218～0.627s，經計算平均暫降后的幅度峰值大概為141.92V，和理論值基本符合，根據IEEE標準此時電壓暫降超過了0.1s，判斷發生了電壓暫降。

2.2 單擾動諧波

在Matlab中的標準工頻信號中加入5次諧波信號擾動，擾動時間為 0.25～0.8s，諧波擾動信號如圖4 所示。

圖4 諧波擾動信號

圖5 諧波擾動時頻關系

通過HHT仿真得到信號時頻關系如圖5所示。從圖5可知HHT算法能準確的檢測出擾動為5次諧波擾動，起止時間為0.248～0.799s。

2.3 間諧波

而對于非整數次間諧波也可以用 HHT法來進行檢測，在0.15～0.77s加入頻率為工頻50Hz的5.5倍幅值為80V的諧波，其諧波表達式為

其信號圖如圖6所示。

圖6 間諧波信號圖

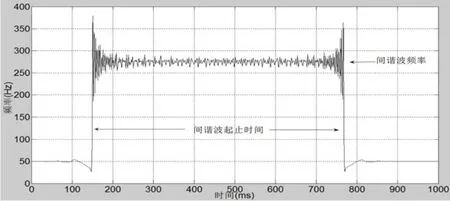
圖7 間諧波分析時頻關系

對間諧波信號進行HHT分析如圖7所示，由圖7也可以看出檢測出的頻率十分接近所給定的275Hz而且起止時間的檢測也是準確的。

由上述仿真，可見HHT法對于單擾動情況下的電壓暫降和諧波均具有較高的靈敏度和精確度

3 復雜多擾動信號的仿真及結果分析

HHT在單一擾動情況下已經有良好的檢測性，但是在電力系統中負載的復雜多樣性和隨機性，以及外部干擾等因素，這些非平穩的暫態信號往往交織疊加形成多擾動信號作用于正常的電力信號[11]。本文在工頻50Hz，幅值有效值為220V，并帶有暫態電能質量多擾動：電壓暫降諧波、電壓暫升諧波、電壓中斷諧波、多諧波的定位及幅值、頻率的檢測為例，運用Matlab仿真驗證。

3.1 電壓暫降、（暫升）諧波檢測仿真

在短時發生單相電壓暫降時，仿真設定相電壓有效值為220V，頻率為50Hz，于0.10～0.85s帶有5次諧波分量，其有效值為80V；在0.30～0.65s 之間發生電壓暫降，其幅值有效值為140V，暫降后幅值為原來的36.36%。電壓擾動信號如圖8所示。對信號進行EMD分解如圖9所示。

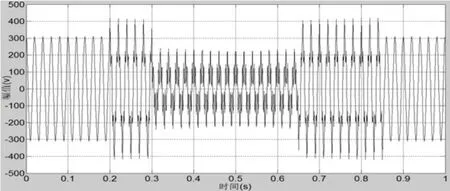
圖8 電壓擾動信號

電壓暫降瞬時頻率如圖10所示，從圖10可以清楚的看出發生擾動的起止時刻和電壓暫降的時刻以及諧波的頻率。瞬時頻率在0.201s 和0.852s 發生跳變，是5次諧波擾動，同時電壓在0.306～0.653s之間發生跌落。由此可以準確地檢測出電壓暫降伴隨諧波發生的起止時間、諧波頻率、電壓跌落幅度如圖11所示。

圖9 目標信號EMD分解

圖10 電壓暫降瞬時頻關系

圖11 電壓暫降瞬時幅值

由圖11可以看出發生擾動的大約起止時刻，電壓暫降的峰值約為110.2V，符合工程應用要求。同樣的方法可以檢測電壓暫升復合擾動。

3.2 電壓中斷諧波檢測仿真

利用Matlab仿真中設定相電壓有效值為220V，頻率為50Hz，在0.2～0.8s之間有幅值有效值為80V的 3次諧波，并于 0.35～0.7s 之間發生電壓中斷，電壓中斷及諧波信號如圖12所示。

圖12 電壓中斷信號

對信號進行 HHT計算分析得到信號的頻率時間關系如圖13所示。

圖13 電壓中斷時頻關系

從圖13可以看出3次諧波伴隨著電壓中斷的出現。在 0.202～0.802s之間發生 3次諧波干擾，在0.351～0.701s發生電壓中斷。其誤差很小，可以得到精確的中斷起止時間，所以HHT檢測電能質量算法在有諧波的情況下對于電壓瞬時中斷的檢測也是正確有效的。

3.3 多次諧波頻率的檢測

諧波仿真中設定信號為標準工頻電壓信號，在不同時間加入3次、5次、7次諧波進行仿真分析，其電壓諧波信號圖如圖14所示；諧波信號HHT分析如圖15所示。

圖14 電壓諧波信號

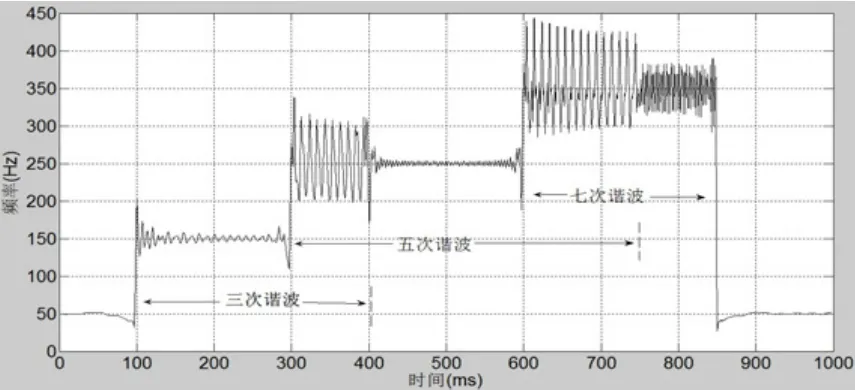
圖15 多次諧波的時頻關系

圖15中可以看出信號含有3種諧波，3次諧波發生時間為 0.101～0.402s，5次諧波擾動的起止時刻為 0.301～0.749s，7次諧波擾動的起止時刻為0.602～0.857s，和理論時刻基本相符合，采用HHT可以準確的找到諧波的含有量、起止時間。

由以上算列仿真可以得出該方法能夠比較準確地檢測出突變、非平穩擾動信號的時間、頻率和幅值的信息。雖然由于端點效應及模態混疊和諧波等問題的影響會產生誤差，但是經過多次測試，基于HHT的多擾動的電能質量檢測的平均誤差很小，能滿足工程要求，可以說本方法對多擾動電能質量的檢測是正確可行的。

4 結論

本文應用HHT算法分別對單擾動和多擾動電能質量信號進行檢測分析。從理論上來講HHT 方法實現了自適應的頻帶劃分，信號分析更加靈活多變。

仿真表明，對檢測的電能質量信號進行 EMD分解，再對得到的各IMF分量求瞬時頻率，可以精確地檢測到擾動信號的發生和終止時刻；結合瞬時幅值的求解方法，可以快速地檢測出擾動信號的幅值；在復雜的電能質量信號下依然有很高的精確度和實時性。該方法簡單快捷，易于實現，能滿足工程需求，適用于電能質量多擾動的監測和辨識系統，應用前景廣闊。

[1]余貽鑫,欒文鵬.智能電網述評[J].中國電機工程學報,2009,29(34):1-4.

[2]王益民. 堅強智能電網技術標準體系研究框架[J].電力系統自動化,2010,34(22):1-6.

[3]張濤,程志友,梁棟,等.非線性主成分分析在電能質量綜合評估中的應用[J].電測與儀表,2008,45(6):5-9.

[4]智能電網關鍵設備（系統）研制規劃[R].國家電網公司, 2010.

[5]徐永海，趙燕. 基于短時傅里葉變換的電能質量擾動識別與采用奇異值分解的擾動時間定位[J].電網技術, 2010,35(8):174-180.

[6]唐求,王耀南,郭斯羽,等.基于 S 變換與 PNN 的電能質量多擾動檢測[J].儀器儀表學報,2009,30(8):1669-1673.

[7]石敏,張紀鈴,徐襲,等.電壓跌落信號參數的檢測[J].微計算機信息,2010,26(35):10-11,122.

[8]HEYDT G T, FJELD P S, LIU C C, et al. Application of the windowed FFT to electric power quality assessment[J].IEEE Transactions on Power Delivery,1999,14(4):1411-1416.

[9]KEZUNOVIC M, LIAO Y. A novel software implementation concept for power quality study[J]. IEEE Transactions on Power Delivery, 2002,17(2): 544-549.

[10]李天云,程思勇,楊梅. 基于希爾伯特-黃變換的電力系統諧波分析[J].中國電機工程學報,2008,28(4): 109-113.

[11]LU Z, SMITH J S, WU Q H. Empirical mode decomposition for power quality monitoring[C].Transmission and Distribution Conference and Exhibition: Asia and Pacific, 2005. IEEE/PES.