(ω,σ)-Sm ash積和(ν,α)-Sm ash余積

鄭乃峰

(寧波大學理學院,浙江 寧波 315211)

(ω,σ)-Sm ash積和(ν,α)-Sm ash余積

鄭乃峰

(寧波大學理學院,浙江 寧波 315211)

設B,H是兩個Hopf代數,構造了(ω,σ)-Sm ash積Bω#σH和(ν,α)-Smash余積Bν??αH,并給出了Bω#σH是Hop f代數和Bν??αH是雙代數的充要條件,證明了許多已知的積和余積是它們的特殊情況.

Hop f代數;交叉積;Smash積;Smash余積

1 引言

最近幾年,很多文章都討論了兩個Hop f代數上的各種積的構造[18].文獻[1]中構造了一種新的Smash雙積,這種積包含了很多在它之前文獻中出現的關于積的構造.例如,通常的Sm ash積[2],扭曲的Sm ash積和扭曲的Sm ash余積[3],D rin fel′d doub le積[4],Doi-Takeuchi′s積[5]等均是它的特例.文獻[6-8]把群交叉積的理論推廣到了Hop f代數上,定義并研究了Hop f代數上的交叉積,Boca給出了交叉積是Hopf代數的充分條件.但是,文獻[1]中的Smash雙積不能包含文獻[6-8]中的交叉積結構,同時,文獻[6-8]中的交叉積也不能包含文獻[1]中的Smash雙積.本文的主要目的是構造一類新的(ω,σ)-Smash積及一類新的(ν,α)-Smash余積,證明了文獻[1]中的Smash雙積與文獻[6-8]中的交叉積都是本文的特殊情況,并推廣了文獻[1]和文獻[6-8]的相應結論.

設K為域,所討論的代數、余代數均指域K上的,所有的映射都是K-線性映射.對于任意一個余代數C及任意的c∈C,采用Sweed ler的記號,記△(c)=∑c1?c2(見文獻[9]).

2 (ω,σ)-Sm ash積

本節先構造了一個代數(ω,σ)-Smash積.然后,利用這種積和張量余積構造了一類新的Hop f代數,證明了許多已知的積是它的特殊情況.為方便,分別記1B為1,1H為^1.

定義2.1設B和H是兩個代數,ω:B?H→H?B是線性映射,?b∈B,h∈H,記

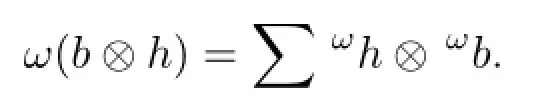
3 (ν,α)-Sm ash余積

[1] Caenepeel S, Ion B, Militaru G, et al. The factorization problem and the smash biproduct of algebras and coalgebras[J]. Alg. Repr. Theory, 2000,3:19-42.

[2] Molnar R K. Semi-direct products of Hopf algebras[J]. J. Algebra, 1977,47:29-51.

[3] Wang S H, Li J Q. On twisted smash products for bimodule algebras and the Drinfeld double[J]. Comm. algebra, 1998,26(8):2435-2444.

[4] Drinfeld V G. Quantum groups[C]//Proceedings of the International Congress of Mathematicians. Provi-dence: Berkeley, 1987.

[5] Doi Y, Takeuchi M. Multiplication alteration by two-cocycle[J]. Comm. Algebra, 1994,22(14):5715-5732.

[6] Blattner R J, Cohen M, Montgomery S. Crossed products and inner actions of Hopf algebras[J]. Tran. AMS, 1986,298:671-711.

[7] Doi Y, Takeuchi M. Cleft comodule algebras of a bialgebra[J]. Comm. Algebra, 1986,14:801-818.

[8] Boca I. A central theorem for Hopf algebras[J]. Comm. Algebra, 1997,25(8):2593-2606.

[9] Sweedler M. Hopf Algebra[M]. New York: Benjamin, 1969.

2010 MSC:16W 30

(ω,σ)-Sm ash p roduct and(ν,α)-Sm ash cop roduct

Zheng Naifeng

(College of Science,Ningbo University,Ningbo 315211,China)

Let B,H be Hopf algebras.W e construct an(ω,σ)-Smash p roduct Bω#σH and an(ν,α)-Smash cop roduct Bν??αH.Necessary and suf cient conditions for the Smash product Bω#σH to be a Hopf algebra and the Sm ash cop roduct Bν??αH to be a bialgeb ra are given.M oreover,m any products and cop roducts are all special cases of Bω#σH and Bν??αH.

Hopf algebra, crossed product, Smash product, Smash coproduct

O153.3

A

1008-5513(2012)02-0167-09

2010-07-12.

浙江省教育廳基金(Y 200906783);寧波市自然科學基金(2011A 610172).

鄭乃峰(1968-),副教授,研究方向：Hopf代數及量子群.