帶非局部積分項常微分方程的討論及其應用

朱一峰,邊保軍

(1.美國埃默里大學經濟系,亞特蘭大 30322;2.同濟大學應用數學系,上海 200092)

帶非局部積分項常微分方程的討論及其應用

朱一峰1,邊保軍2

(1.美國埃默里大學經濟系,亞特蘭大 30322;2.同濟大學應用數學系,上海 200092)

研究帶非局部積分項的二階線性常微分方程及其在金融保險上的應用.首先討論帶非局部積分項的二階常微分方程解的存在唯一性,通過變量代換和累次積分交換積分順序將非局部項簡化,將方程化為方程組,然后完成了對方程組解的存在唯一性的證明.接著分析了帶非局部項的二階常微分方程解的結構,給出了方程解的形式.最后通過推導,指出帶非局部項的線性常微分方程在保險公司的破產概率研究中的應用,重點放在二階方程的應用上,并且在某一特定情況下,舉出了一個可以給出解析解的例子.

非局部積分項;二階常微分方程;破產概率

1 引言

1997年4 月25 日,日本互助生命保險公司宣告破產,結束了“日本保險公司不倒的神話”時期,接下來東邦生命,第百生命,第一火災海上等保險公司也相繼倒閉,進一步影響了人們對保險公司的信任度.美國也從1989年“黑色星期一”起,保險公司破產數量明顯增加.受2008年全球金融風暴的影響,使中國正在發展的保險業受到了懷疑.怎樣有效地降低保險公司破產概率,繼而保證保戶的利益成了人們更加關心的話題.相關的研究從文獻[1]開始,近期的研究則集中于基本模型下增加考慮因素及提供一些解析解,文獻[2-3]即考慮了稅負因素.

本文就是要研究破產概率所涉及到帶非局部積分項的常微分方程.如果考慮風險投資,破產概率所滿足的微分積分方程就是二階方程,如果不考慮,所滿足的方程就是一階的.最后在特定情況下,給出方程的解.說明哪些因素可以影響保險公司的破產概率,這同時也說明這類方程有著非常廣泛的應用背景.

2 帶非局部積分項的二階常微分方程初值問題解的存在唯一性

本文主要討論帶非局部積分項的二階常微分方程,先給出方程的一般形式:

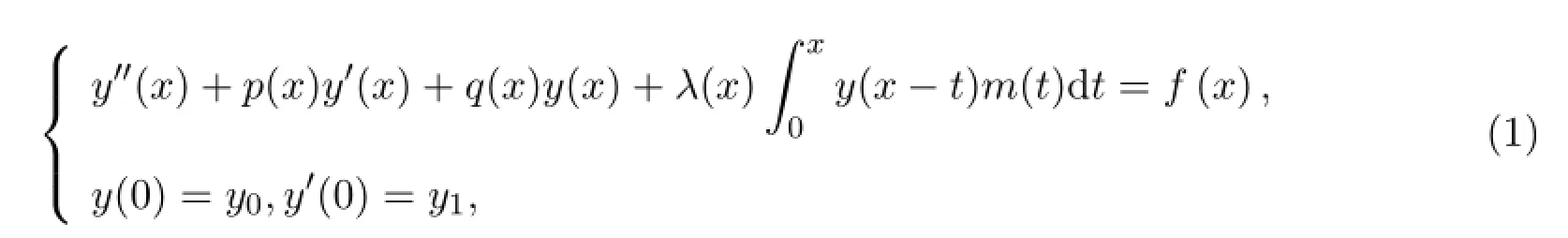
其中p(x),q(x),λ(x)是非常系數.

考慮定解問題(1)解的存在唯一性.令y′(x)=z(x),得到

3 帶非局部項的二階常微分方程解空間的結構

這里c1,c2是相應的確定常數.

所以,可知(8)式的線性無關解最大個數等于2,(8)式的所有解的集合構成一個2維線性空間.

定理3.3,定理3.4可以表述為:

定理3.5(8)式一定存在一個基解矩陣φ(x),如果ψ(x)是(8)式的任一解,那么

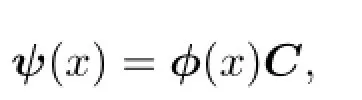
這里C是確定的常數列向量.

(8)式的兩個簡單性質:

性質3.1如果ψ(x)是(7)式的解,φ(x)是(7)式的對應的齊次方程組(8)式的解,則ψ(x)+φ(x)是(7)式的解;

性質3.2如果?ψ(x)和?φ(x)是(7)式的兩個解,則?ψ(x)-?φ(x)是(8)式的解.

由性質2.2和定理2.5,可得如果φ(x)是(8)式的基解矩陣,fiφ(x)是(7)式的某一解,則(7)式的任何一解ψ(x)都可表為

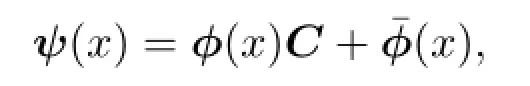
這里C是確定的常數列向量.

4 在保險公司破產概率計算中的應用

帶非局部積分項的常微分方程在金融方面有著廣泛的應用,尤其是在計算保險公司破產概率時.設u＞0是保險公司初始準備金,保費收入按照固定比例c＞0隨時間線性增長,即[0,t]期間保費收入為ct,用S(t)表示理賠額,Wt代表t時刻保險公司用以投資所得的不確定收入,則保險公司在時刻t時的盈余Rt,可以用下式簡單表示出來:

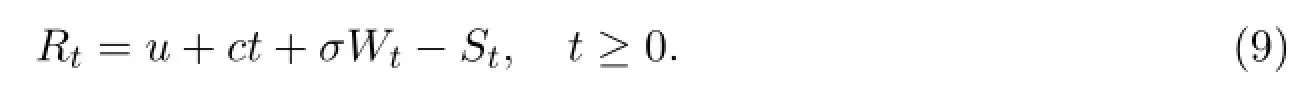
在(9)式中,理賠{S(t)}是依賴于時間的隨機變量,即隨機過程.理賠過程{S(t)}由理賠次數(過程){N(t)}與每一次個別理賠額{Zk,k=1,2,…,Nt}復合而成.若是理賠次數N服從泊松分布,則稱聚合理賠量S服從復合泊松分布.(9)式中σ＞0表示原生資產的波動率常量,{Wt}標準布朗運動.

下面在經典風險模型下討論問題:

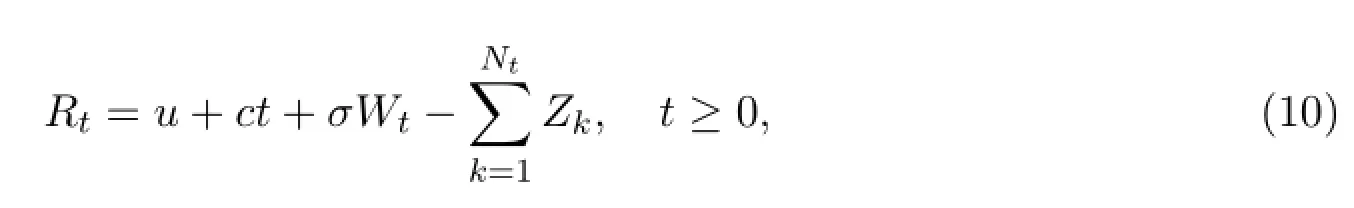
其中{Nt}是參數為λ＞0的泊松過程,在時間段(0,t)上記錄下了理賠的次數;{Zk},k≥1是相互獨立的非負的隨機變量序列,Zk表示第k次理賠額.{Nt},{Zk},{Wt}相互獨立.(10)式過程是連續時間的齊次強馬爾可夫過程.

從(10)式中可以看出有兩種可能性會導致保險公司的破產.一是由理賠所引發的破產,一是由于公司的投資不當所造成的破產.所以,文獻[5]將(10)式的風險過程的破產概率分解成兩個部分:由投資不當所造成破產的概率和由于理賠所造成破產的概率.假設破產概率是二階可微的,他們得到了以級數明確表示的兩種不同的破產概率.

說明增加保險公司的初始準備金,或提高費率,可以有效降低破產概率.若考慮了利率因素,因為所化成的方程中的系數不再全是常系數,所以解答起來和上面的方法有所不同,比較復雜,不過仍然可以用顯式表達破產概率,本文不再累述.

參考文獻

[1] Gerber H U. An extension of the renewal equation and its application in the collective theory of risk[J].Scandinavian Actuarial Journal, 1970(3):205-210.

[2] Albrecher H, Borst S, Boxma O, et al. The tax identity in risk theory-a simple proof and an extension[J].Insurance: Mathematics and Economics, 2009,44:304-306.

[3] Wang W, Ming R, Hu Y. On the expected discounted penalty function for risk process with tax[J]. Statist.Probab. Lett., 2011,81:489-501.

[4] 王高雄,周之銘,朱思銘,等.常微分方程[M].2版.北京:高等教育出版社,1983.

[5] Dufresne F, Gerber H U. Risk theory for the compound Poisson process that is perturbed by diffusion[J]. Insurance: Mathematics and Economics, 1991,10:51-59.

[6] Revuz D, Ypr M. Continuous Martingales and Brownian Motion[M]. Berlin: Springer, 1991.

[7] Port S, Stone C. Brownian Motion and Classical Potential Theory[M]. New York: Academic Press, 1978.

[8] Wang G, Wu R. Some distributions for classical risk process that is perturbed by diffusion[J]. Insurance:Mathematics and Economics, 2000,26:15-24.

[9] Gerber H U, Shiu E. From Ruin Theory to Option Pricing[M]. Cairns: AFIR Colloquium, 1997.

Discussion and application of ordinary differential equation with non-local integral term

Zhu Yifeng1,Bian Bao jun2
(1. Department of Economics, Emory University, Atlanta 30322, USA; 2. Department of Applied Mathematics, Tongji University, Shanghai 200092, China)

Second-order linear ordinary differential equation with non-local integral term inside are major discussed in this thesis. Firstly, we canvass the existence and uniqueness of the solution of the second-order ordinary integro-differential equation. By variable substitution and exchanging sequence of repeated integral, the non-local integral term can be simplified, the equation can be transformed into system of equations. Then, the proof of existence and uniqueness of the solution of equations are completed here. Second, we analyze the structure of the solution, also we give the solution form of the equation. At last, we point out the application of the ordinary integro-differential equation through deduction. It can be used in ruin probabilities′ of an insurance company. We focus our energies upon the application of the second-order equation. Furthermore, the explicit expressions for the integro-differential equations will be presented when the claims are exponentially distributed.

non-local integral term, second-order differential equation, ruin probability

O 175.1

A

1008-5513(2012)02-0219-09

2011-08-26.

朱一峰(1983-),博士生,研究方向:偏微分方程,金融經濟學.

2010 MSC:91B30