抗艾滋病藥物的評價與預測模型

鄧麟,顧立偉,王鋒剛,王經民

(西北農林科技大學,陜西 楊凌 712100)

抗艾滋病藥物的評價與預測模型

鄧麟,顧立偉,王鋒剛,王經民

(西北農林科技大學,陜西 楊凌 712100)

第一問中對CD4數量和HIV濃度隨周期變化分別建立線性模型和二次模型,由數據確立中度患者CD 4隨時間變化模型為:C(T)=0.0496T+3.0659,HIV隨時間變化為:H(T)=0.0044T2-0.2317T+4.2899.確定最佳治療終止時間為:輕度患者28.90周,中度患者31.97周,重度患者為40.86周,平均最佳終止治療時間33.91周.第二問中得出療法4效果最好,療法3次之,療法1最差.然后通過建立了回歸分析模型,對最優療法進行預測,得到最佳終止治療時間為25.53周.第三問在第二問的基礎上增加了治療費用對治療效果的影響,計算得出:療法3為最優,療法1次之,療法2最差.用療法3的數據進行作圖分析得到療法3的最佳治療終止時間為40周.

CD 4;HIT;健康指數;模糊綜合評判;評價比

1 問題的重述

艾滋病是當前人類社會最嚴重的瘟疫之一,英文簡稱AIDS,它是由艾滋病毒(英文簡稱HIV)引起的.這種病毒破壞人的免疫系統,使人體喪失抵抗各種疾病的能力,從而嚴重危害人的生命.人類免疫系統的CD4細胞在抵御HIV的入侵中起著重要作用,當CD 4被HIV感染而裂解時,其數量會急劇減少,HIV將迅速增加,導致AIDS發作.

艾滋病治療的目的,是盡量減少人體內HIV的數量,同時產生更多的CD4,至少要有效地降低CD4減少的速度,以提高人體免疫能力.現在得到了美國艾滋病醫療試驗機構ACTG公布的兩組數據.ACTG320是同時服用zidovudine(齊多夫定),lam ivudine(拉美夫定)和indinavir(茚地那韋)3種藥物的300多名病人每隔幾周測試的CD4和HIV的濃度(每毫升血液里的數量).將1300多名病人隨機地分為4組,每組按下述4種療法中的一種服藥,大約每隔8周測試的CD 4濃度(這組數據缺HIV濃度,它的測試成本很高).4種療法的日用藥分別為:600mg zidovudine或400mg didanosine(去羥基苷),這兩種藥按月輪換使用;600mg zidovudine加2.25 mg zalcitabine(扎西他濱);600 mg zidovudine加400 mg didanosine;600 mg zidovudine加400mg didanosine,再加400mg nevirapine(奈韋拉平).請你完成以下問題:

(1)利用所給的數據,預測繼續治療的效果,或者確定最佳治療終止時間(繼續治療指在測試終止后繼續服藥,如果認為繼續服藥效果不好,則可選擇提前終止治療).

(2)利用所給的數據,評價4種療法的優劣(僅以CD 4為標準),并對較優的療法預測繼續治療的效果,或者確定最佳治療終止時間.

(3)艾滋病藥品的主要供給商對不發達國家提供的藥品價格如下:600mg zidovudine 1.60美元,400mg didanosine 0.85美元,2.25 mg zalcitabine 1.85美元,400 mg nevirapine 1.20美元.如果病人需要考慮4種療法的費用,對(2)中的評價和預測(或者提前終止)有什么改變.

2 基本假設

1由于測試的患者病情程度不同,假設可以分為輕度、中度和重度患者,分類相同的所有患者可以視為一個人來處理;

2假設在病毒產生抗藥性之前,CD4細胞數量與用藥時間成線性關系;

3服藥時間的長短與健康系數的自然對數成反比;

4假設測試的患者均沒有因受到其它疾病感染而使H IV和CD 4數量發生很大波動;

5在用藥的情況下,如果艾滋病患者體內的HIV濃度增長率大于了CD4數量的增長率時,假設這種藥對艾滋病的療效不理想,沒有必要再繼續服用下去;

6假設四種療法的費用只包括藥物的費用.

3 符號說明

T艾滋病患者開始服藥以來的時間(單位:周);

H(T)T周時艾滋病患者體內的HIV病毒濃度;

C(T)T周時艾滋病患者體內的CD4的濃度;

W在采用某一種療法時各個年齡段在該療法中的權重分配向量;

R在評價四種療法過程中僅以CD4數目為標準時的單因素評判矩陣;

A四種療法的模糊評判矩陣;

i治療方法,取1,2,3,4;

Pi采用第i種療法所用藥品的周費用(單位:美元,i=1,2,3,4);

δi采用第i種療法治療時患者體內的CD4數量隨時間的平均變化率;

Mi第i種療法的性價比(即治療效果和用這種方法所用藥品費用的比值).

4 問題分析

此題目要求以數據為基礎建立合適的AIDS藥物治療效果的預測和評價模型,但需要對數據篩如測試周期較少而且兩個指標CD4細胞數量和HIV病毒濃度測試不同步等.

考慮到測試患者的健康程度具有差異性,即使同步測試的患者(如都從0開始測試)其CD4數量與HIV濃度變化也是不同的.于是可以考慮用一個健康系數把患者分為三類:輕度患者、中度患者和重度患者,從而把數據進行聚類分析.

開始用藥時,H IV病毒會被大量殺滅,數目會有一個快速下降過程,而CD 4數量會呈上升趨勢.由于微生物會產生突變和抗藥性,當HIV對藥物完全抗藥后就會又大量繁殖,又會呈上升趨勢,于是可以假設HIV濃度隨時間服從二次曲線規律,而CD 4數量隨時間服從線性規律.

當HIV產生抗性后增長的速率(二次曲線的斜率),超過CD 4增長速率(直線斜率)時,藥物已經完全失效,此時為最佳的治療終止時間.

問題二要求對四種療法的優劣性進行評價,由于數據較復雜且評價指標CD4隨著年齡不同和治療時間長短有著差異性,同時評價指標又僅有CD4一個,考慮用單級模糊綜合評判來對四種療法的優劣性進行評價.復雜數據需要進行分組:按年齡分組,屬于以不同年齡段的個體為單位,結果可能會更符合常規;而按周期分組屬于不考慮因年齡的不同個體之間存在著差異,以整體的治療時間為單位對整個用藥過程進行分析這樣的結果可能會在理論上更準確.通過評價確定出較優的療法,對其進行預測,這里考慮用回歸的方法建立模型進而判斷治療效果.

問題三只是在問題二的基礎之上增加了一個費用因素,于是可以設法把該因素和問題二中的某些指標聯系起來,產生出新的數據,從而使得費用的加入對第二施加影響,從而建立新的評價及預測模型.

5 模型建立與求解

問題一

1)模型的建立

由分析與假設:病毒產生突變和抗藥性,使得HIV濃度(H)在服藥后先下降后上升,HIV濃度(H)與時間(T)在一定范圍內成二次曲線,即

又因為病毒產生抗藥性之前,CD4數量(C)與時間(T)成線性關系,于是有

由于開始用藥時HIV病毒是受到抑制的,一定時期內其數量會減少,隨后產生突變和抗藥性使得藥物效果降低,HIV濃度及其增長速率不斷變大(二次曲線切線斜率),當超過CD4增長速率時是最佳治療終止時間,即函數(1)的導數大于函數(2)的導數:2a2T+a1≥b1,于是

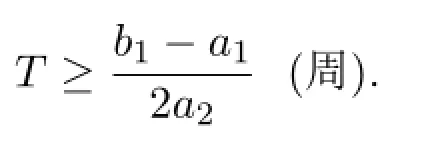
2)模型的求解

先對給定的300名患者的觀察數據用Excel進行處理,求得測試期間各周內患者的平均CD 4細胞數目以及HIV病毒濃度,在同一坐標系內做出二者的關系圖(如圖1橫坐標為時間,縱坐標為CD4細胞數量或HIV濃度).

從圖中可以看出CD4與HIV呈現相反的趨勢,符合實際,但是由于給定的300多名患者的病情程度不同,而且數據測定的時間以及次數不同,所以不能用平滑或者平移的方法進行預測.由于數據量大且患者的健康程度不一致,要剔除數據中的奇異點選出合理的數據并進行適當的數據壓縮.

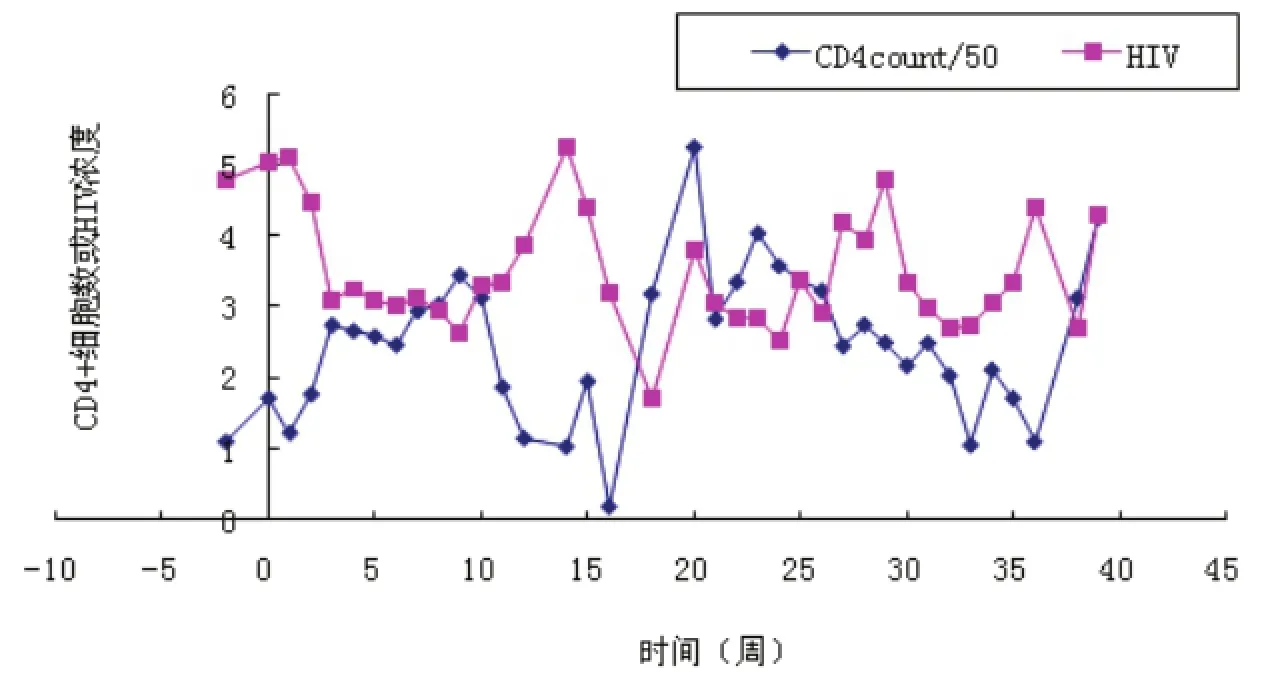
圖1 CD 4數量和HIV濃度隨時間的變化曲線

由假設,根據被測試患者的健康程度不同將其分為三個等級:輕度、中度和重度.從而對數據進行聚類,具體步驟如下:

1.數據的初級篩選.去掉測試次數少,且有缺失數據的患者,篩選出科學合理的數據,保留測試具有代表性(HIV和CD 4同步測試且次數較多)的數據,最后選定測試周數為40周且完整的數據.

2.確定分類指標.定義每名患者測試期間的CD4與HIV含量的比值的平均值為健康指數,即

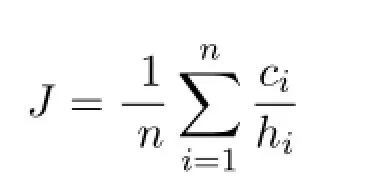
上式J為患者的健康系數,n為測試次數,ci、hi分別為患者在某次測試時的CD 4細胞數目和HIV病毒的濃度.

3.計算得到各患者的健康系數,進行排序和統計.把數據分為三組(表略).

4.數據細處理.統計出測試時間為40周的各類患者在各周內的CD 4細胞數目和HIV病毒的濃度平均值.由假設,同一類患者可以看作一個人來處理.于是就可以把三類患者看作三個人來進行預測和評價.經計算得到輕度和中度患者的各時間段內的指標,考慮到數據的科學性和比較的方便性,同時取兩種患者的0、4、8、25、40周的數據作圖進行比較和分析(如圖2,圖3):

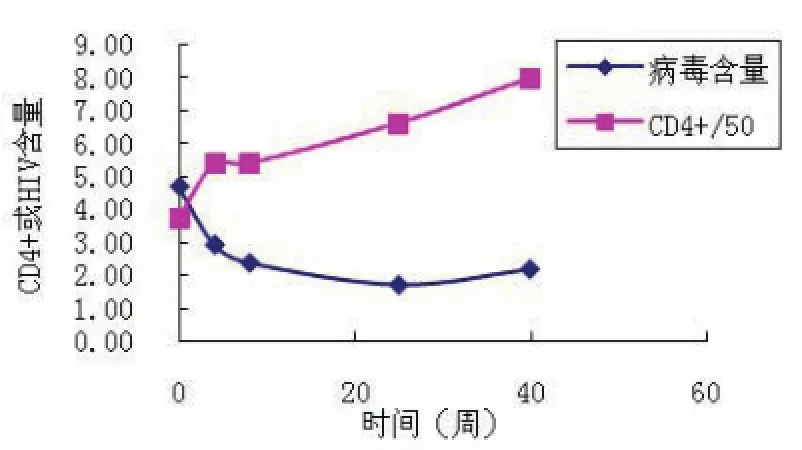
圖2 輕度患者CD 4和HIV隨時間變化

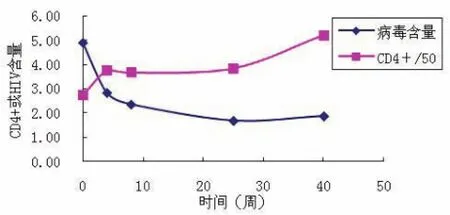
圖3 中度患者CD 4和HIV隨時間變化

從兩種病情不同的患者可以發現在測試期間CD 4數量呈上升趨勢,而HIV的濃則是先快速下降,然后緩慢下降最后又開始回升.說明在藥物的治療下CD 4含量不斷上升,但是HIV病毒也在不斷產生突變和抗藥性,使得服用的藥物無法發揮作用.因此,隨著服藥時間的延續,治療效果就越來越不明顯.

又由病毒產生突變和抗藥性,使得HIV濃度在服藥后先下降后上升,HIV濃度與時間成二次曲線;對中度患者CD4和HIV含量分別對時間進行曲線擬合[1](如圖4):

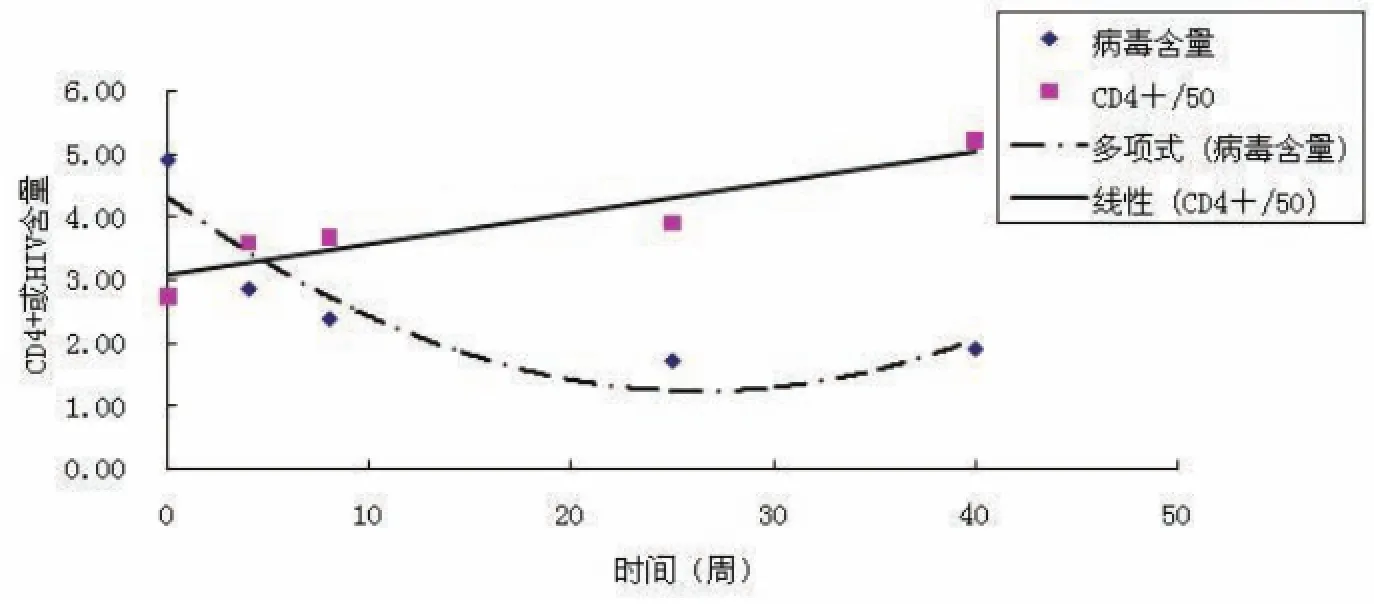
圖4 中度患者CD 4和HIV含量曲線擬合

得到的擬和方程分別為:

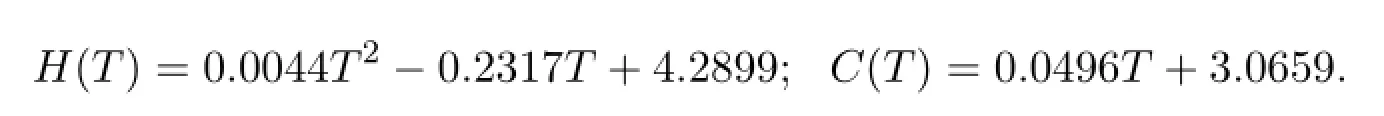
當HIV濃度增長率大于CD 4的增長率時,說明該藥物對艾滋病已經不再有療效.所以,當HIV濃度增長率等于CD 4的增長率時正是停藥的最佳時間.由此得到中等患病者的最佳治療終止時間滿足以下關系:

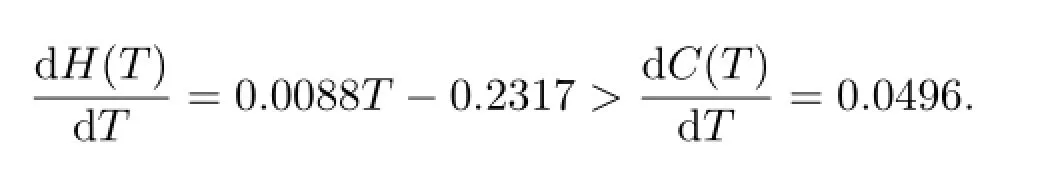
于是T=31.97周.

接著由基本假設服藥時間的長短與健康系數的對數成反比,即T ln(J)=常數,并且結合分類時的統計數據中健康指數(如表1)就可以求出輕度患者和重度患者的最佳停藥時間.

表1 統計數據中健康指數

綜上計算可知:輕度患者、中度和重度患者的最佳治療終止時間分別為:28.90周、31.97周和40.86周,平均最佳治療終止時間為33.91周.

問題二

1)模型的建立:藥物效果模糊綜合評判模型[2].

這里要評價是四種不同用藥的效果,用模糊綜合評判法,對各個年齡段的治療情況整體進行分析.評價模型可以分為以下幾個層次:

1.目標層:表示解決問題的目的,即綜合評價四種藥物的治療效果.

2.準則層:表示采取某種措施,來實現或論證預定的總目標所涉及的中間環節,在此用各個年齡段的藥物治療效果(xi)作為準則層.

3.指標層:即評價時具體考慮的指標,在此用四類藥物(yi)作為指標.

用附表給出的多組觀測資料,按照規定統計出各評語的頻率,構成R=X×Y=(rij)上的評價關系矩陣,其中rij為因子xi對分類級別yj的頻率,其計算公式為:

把年齡段的數據進行進行模糊化,得到權重(w1,w2,w3,w4,w5,w6).最后對其進行綜合評價值得到,其實現方法如下:

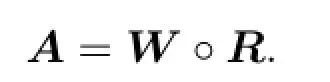
其中W為權重距陣,R為關系距陣.運算符“?”與矩陣的乘法類似,區別在于將矩陣乘法中的乘號以取小代之,加號以取大代之.

2)模型的求解(對四種療法進行評價):

由于采取某一種療法的人數是通過對1300多名病人隨機的分組產生的,且采用每個療法的人數大致相等.在人數較多的情況下,需要考慮不同個體之間的差異,于是,按照對每一種療法不同年齡段的個體為單位,進行分組.用V isual Basic[3]程序進行統計分組.按照年齡段分組,提供的數據中最大年齡為74.193,最小年齡為14.9021,極差為59.2909.為了使結果更具有可信性將其分為六組,組距為10.由統計結果看出采取每種療法的每個年齡段的人數也基本相同,為了確定各齡段在某一種治療方法中所占的權重,先應對各年齡段按療法進行歸一化處理.

據統計結果看出各個年齡段的權重在各療法中差異性不大,在保證計算在一定程度上具有說服力的基礎上,為了降低解決問題的成本,取每個年齡段在各療法間權重的均值來作為各年齡段的權重分配向量代入問題二中建立的模型得:

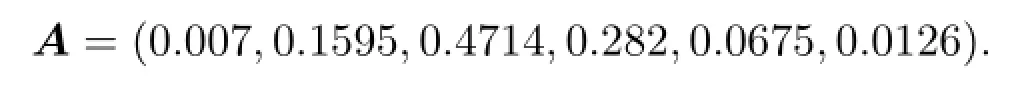
為了能反映艾滋病人在服藥過程中體內CD4的數目隨時間的變化情況,以Log(CD 4 count+1)在測定時間內的平均變化率(/周)作為單因素評判矩陣.但在這里變化率大多數為負值,意味著在治療過程中患者體內的CD 4數目反而下降了,出現負值進行歸一化處理將使評價結果的合理性大大降低.但發現在結果要求的精度范圍內,病人體內的CD 4數目也能在一定程度上反映治療的效果.于是,在同一年齡組內不考慮個體之間差異的情況下,用某一療法在相應的年齡組內的病人體內CD4數目的均值來代替前面的變換率建立單因素評判矩陣,然后做模糊變換來求四種療法的評判矩陣(向量):

其中W為權重距陣(向量),R為關系距陣.運算符“?”同上.則有:

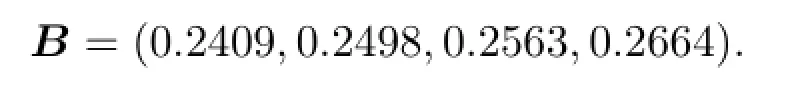
將評判結果歸一化得:

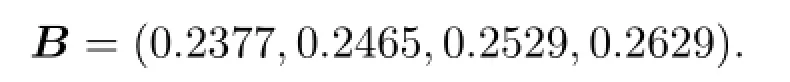
這表明四種療法中最優的為第四種,其次為第三中,再次為第二種,最差的為第一種.

3)對較優的療法進行預測:即就是對第四種療法進行治療效果的預測,對療效的預測需要考慮在采取某種療法的情況下隨著時間的推移,艾滋病患者體內的CD 4數量的變化情況.

按照病人采用不同的治療方法將其分為四個組,即采用治療方法1-方法4進行治療的病人數據各為一組.然后在每一組中根據所有病人在用藥后進行Log(CD 4 count+1)檢測的時間順序將其再次分組.總共的檢測時間為從第0周到第40周,因為大約每隔8周測試一次CD 4濃度,所以以8作為組距,分為五個時間組,即:[0,8],(8,16],(16,24],(24,32],(32,40].

通過計算得出各個時間段內的所有病人所測得的Log(CD 4 count+1)的平均值,將其作為時間組的Log(CD 4 count+1),然后再求出不同的治療方法在各個時間組的Log(CD 4 count+1)的平均值.

利用各種治療方法的各個時間組平均數來作圖觀察比較(如圖5-圖8):

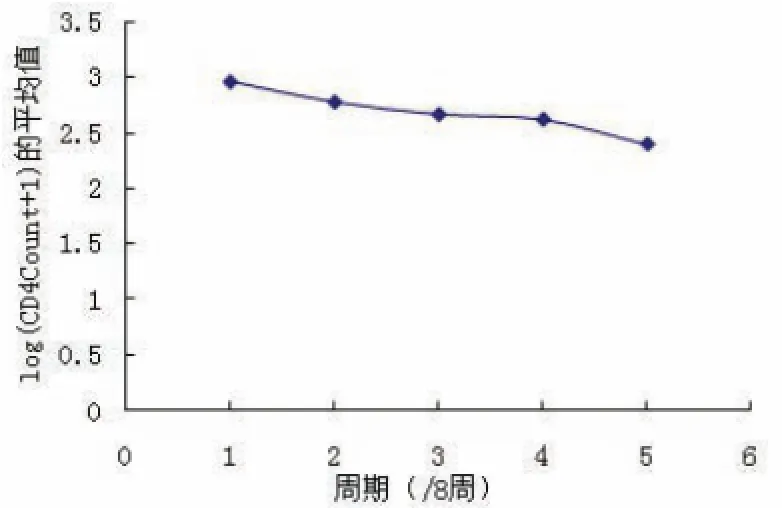
圖5 治療方法1 CD 4隨周期變化圖

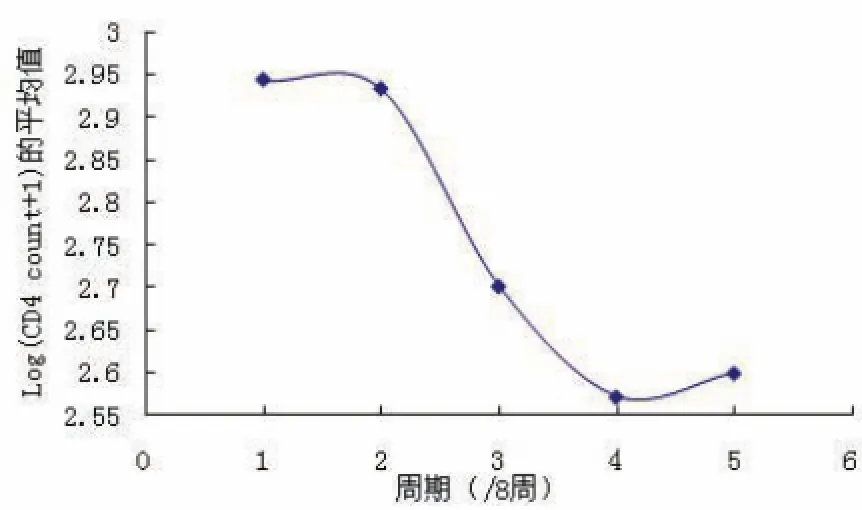
圖6 治療方法2 CD 4隨周期變化圖

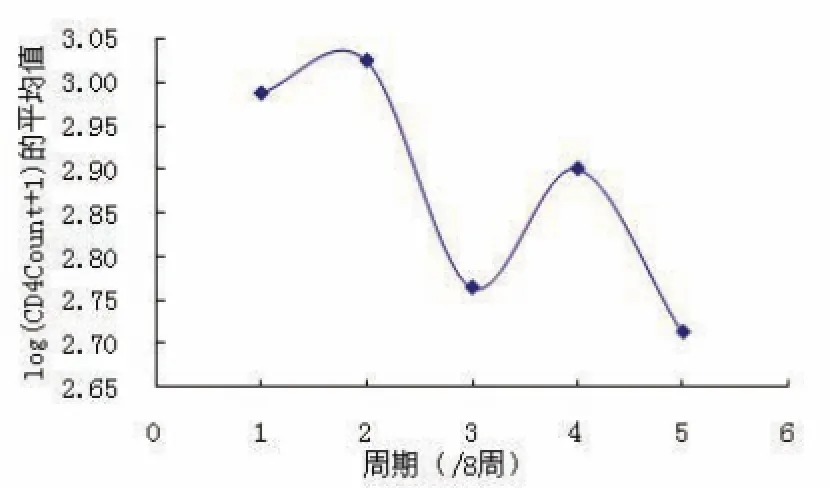
圖7 治療方法3 CD 4隨周期變化圖

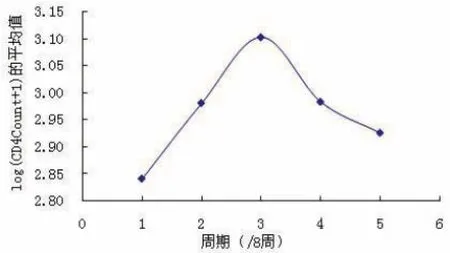
圖8 治療方法4CD 4隨周期變化圖

從以上四種藥物組合方式的CD 4含量對周期的變化圖,可以發現四種藥物的效果有明顯的不同.治療方法1比較符合線性規律,但是斜率很小說明其藥物效果不好;治療方法2先時有緩慢的上升然后時急劇地下降,效果也不好;治療方法3雖然有一定效果,但是波動性比較大;治療方法4基本符合二次曲線規律,先是快速地上升過程,然后是下降,但是它的CD 4平均水平較高,是較優的治療方法.

下面用二次曲線進行擬合(見圖9).

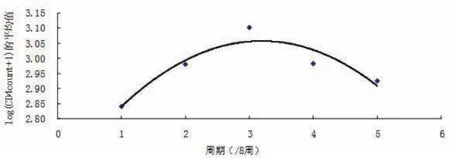
圖9 治療方法4中CD 4療效預測圖

擬合的方程為:

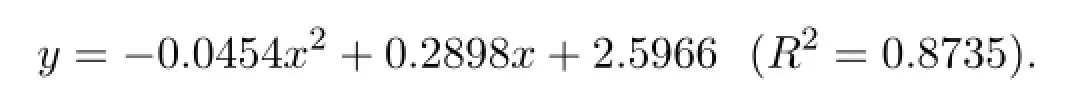
在CD 4細胞數量達到最高值處,即CD 4增長速率為零(二次曲線的切線斜率)為最佳的治療終止時間.于是對上述擬和方程求導得到:

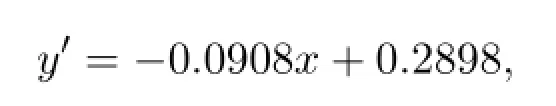
令上式為零,得到x=3.192(周期),一個周期為8個周,于是最佳的治療終止時間為25.53周.

問題三

由于需要考慮治療費用,于是先對各種治療方法的平均費用(每周)進行計算.第一種療法的費用:第一種療法為兩種藥物按月輪換使用,因此它的費用為兩種藥物價格的平均值.由于檢測是以周為單位,故也將費用化為周費用.

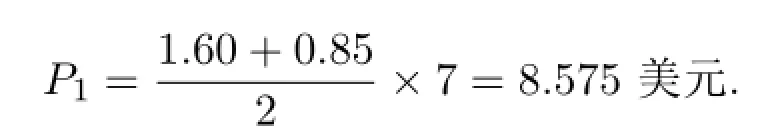
第二種療法的費用:第二種療法為兩種藥物聯合用藥,故其費用為兩者之和

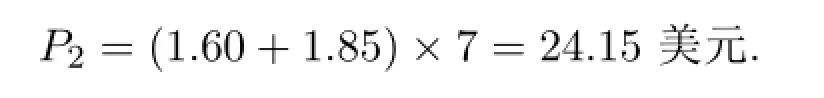
第三種療法的費用:第三種療法同樣為兩種藥物聯合用藥,故其費用為兩者之和.

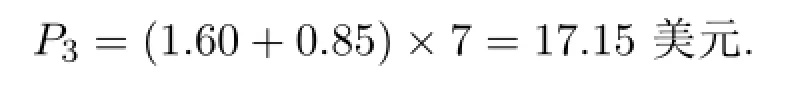
第四種療法的費用:第四種療法為三種藥物聯合用藥,故其費用為三者之和,

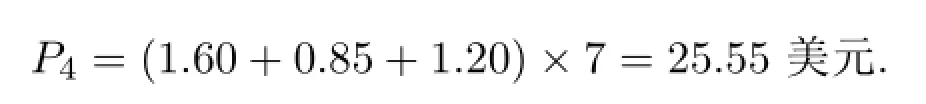
然后對該矩陣按照行(即每個年齡段看作一個整體)來進行歸一化處理,得到以下的評判矩陣.同樣,做模糊變換來求四種療法的評判矩陣(向量):

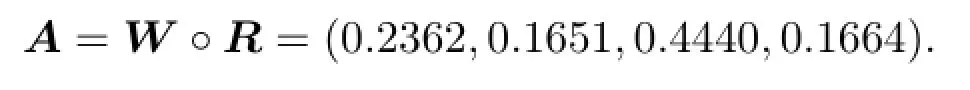
進而對該評判矩陣進行歸一化處理,得A=(0.2335,0.1632,0.4389,0.1645).

這表明在考慮費用的情況下四種療法中最優的為第三種,其次為第一種,而第二種和第四種療法的療效比較接近,第四種稍優于第二種.

對第三種療法進行繼續治療效果的預測(見圖10):

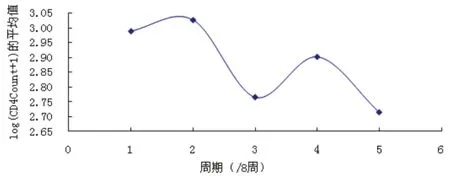
圖10 治療方法3 CD 4隨周期變化圖

由已知的治療方法3 CD4隨周期變化圖,不難看出CD 4含量式先緩慢上升而后迅速下降到一定水平,然后再次上升(從圖中可以看出此時為第4周期),隨后一直下降到很低的水平.因此不用曲線擬合直接可以得出最好的治療終止時間為第4個周期,即就是開始用藥后的第32周.

6 模型的檢驗及科學性分析

對第一問中的模型利用Excel里面分析工具庫[4]中的回歸對所建立的回歸方程進行F檢驗[5],檢驗的結果如下:

(1)以下是對患者CD 4/50與治療時間的線性回歸方程的檢驗結果(見表2):查表

表2 F檢驗的結果

得:F0.05=10.13＜18.25802,所以建立關于患者CD 4/50與治療時間的線性回歸關系顯著.

(2)以下是對患者HIV含量與治療時間的二次多項式回歸方程的檢驗結果(見表3):

表3 F檢驗的結果

查表得:F0.05=10.13＜15.480478,所以建立的關于患者HIV含量與治療時間的二次多項式回歸方程關系顯著.

對于統計的結果和假設的模型比較符合,第二問使用的擬和的方法,直接從擬合曲線即可得道其正確性.第三問由圖形觀察得出,不必進行檢驗.

7 模型的評價與改進

在三個問題中,第一問是把數據通過引入一個健康指數而把CD4細胞數量和HIV濃度很好的連接起來,進行很好地聚類,處理的結果證明了模型的正確性.第二問用模糊綜合評判法可以把大量的數據予以簡化并且量化,使得復雜的關系變得清晰,不失為一種很好的數據處理方法.第三問通過引入性價比的概念,重新構造矩陣進行評價和預測,從而完善了第二問的不足,也是比較可行的.

在建模中面對大量復雜的數據在一定精度范圍內為了分析和評價方便采取的大量簡化,大多通過取均值來計算,可能會對計算的科學性有一定影響,如能采用加權平均或更實際的方法,可能效果會更好.另外,如能結合藥理分析等方面的知識,將會使建模過程更加豐富,這些都是模型值得改進的方面.在對繼續治療效果的預測方面,若能借鑒灰度GM(1,1),BP神經網絡等更高級的建模方法,將會使建模過程變得更加完美

[1]劉來福,曾文藝.數學模型與數據建模[M].北京:北京師范大學出版社,2002.

[2]曹謝東.模糊信息處理及應用M]北京:科學出版社,2003.

[3]李書琴.V isual Basic 6.0程序設計教程[M].西安:西北大學出版社,2004.

[4]邵崇斌.概率論與數理統計[M].北京:中國林業出版社,2003.

[5]張勤,張啟能.生物統計學[M].北京:中國農業大學出版社,2002.

The evaluation and prediction model of the effect of AIDS therapy

Deng Lin,Gu Liwei,Wang Fenggang,Wang Jingm in

(Northwest A&F University,Yangling 712100,China)

In first section, we set up linear and quadratic model for density of CD4 and HIV with time.Amount of CD4 of middle sufferer with time satisfy: C(T) = 0:0496T + 3:0659 , Amount of HIV: H(T) = 0.0044T2-0.2317T+4.2899.Stopping therapy best time: early, middle and late sufferer are: 28.8th week, 31.97th week and 40.8th week. Average best stopping time is 33.91th week. In second section, the result show that treatment 4 is best one, after treatment 3; treatment 1 is bad. We set up regress model for treatment 4, and predict best stopping time: 25.53th week. Based on the second section, the third section add the in°uence of cost to effect of treatment. By fuzz judge matrix, show that treatment 3 is the best one, after treatment 1;treatment 2 is bad. Through the graphical analysis, stopping therapy best time for treatment 3 is 40th week.

CD4, HIV, health index, fuzz general evaluation, ratio of effect with cost

O 175.12

A

1008-5513(2012)02-0275-10

2011-05-10.

西北農林科技大學教學改革研究項目(JY 0902109).

鄧麟(1986-),博士生,研究方向：基因序列分析.

獲獎等級：2006年全國大學生數學建模競賽全國二等獎.

2010 MSC:34D 05