非線性機械系統PID控制漸近穩定性分析

馬唯一

1.上海市采埃孚轉向系統有限公司，上海 200062

2.上海交通大學自動化系，上海 200240

雖然當前控制理論與技術實現了持續的發展和進步，同時人們也提出了不同的非線性比例的積分和微分方程，有效改善了傳統線性PID品質，但大多數的實際機械控制系統依舊采用傳統的線性PID進行控制。而PID控制的非線性機械系統的穩定性分析一直是研究中的難點。

Arimoto提出了不確定的非線性機械系統PID局部控制趨向穩定性，而Kelly則提出根據飽和函數在實踐中的引入明確了非線性不確定機械系統控制的全局漸進穩定性。相應的專家還了解到自適應飽和P加D控制過程中所呈現的機械系統全局穩定性特點。根據近期的文獻研究了解到，專業的研究者所提出的新型的飽和函數，有效證明了P加D飽和同步誤差的非線性控制機器人系統的全局漸進穩定特點。

1 機械系統動力學模型與特性

n自由度的自由度旋轉關節非線性機械系統動力學模型描述如下：

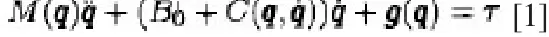
上述公式中，q為關節位置， 為速度矢量， 為加速度矢量，M（q）為對稱正定慣性矩陣，而B0為關節線性阻尼摩擦力矩陣，C(q，)為哥氏力以及離心力矩陣，而g（q）是重力向量，U(q)是由于重力而形成的勢能，而則是力矩控制矢量。

非線性機械系統一般具有一下所示的結構特性：

1）當B0，實際上也是線性阻尼矩陣為對角正定矩陣，慣性矩陣保持對稱正定且并非無限，是有界的，其范圍滿足如下關系式：

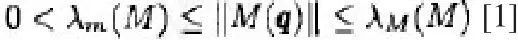
其中的λm（M）以及λm(M)表示的是在M（q）矩陣中的最小特征值和最大特征值。

2）對于特定的qd以及任意的q以及α＞0，有一個恒定的對角正定矩陣保證下列關系式成立：

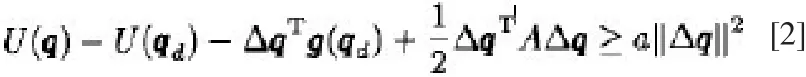
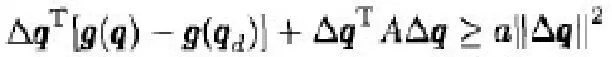
上述公式中Δq= q- qd為關節誤差，而qd與q分別為期望以及實際的位置。

在實際的分析過程中，也就是公式中，對于任意的qd，也就的任意給定的期望位置，設計出線性PID控制器，通過綜合的考量能與任何的模型信息適用，同時實現了非線性機械系統漸進穩定性位置的控制，從而致使非線性機械系統從初始的位置漸進穩定達到目標狀態。

2 非線性機械系統PID控制漸進穩定性分析

2.1 傳統線性控制半全局漸近穩定性

傳統PID線性控制:

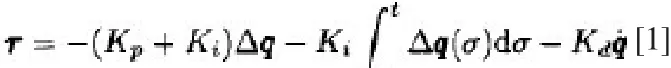
公式中的Kp+Ki為恒定對角正比例，而Kd為微分增益矩陣；Ki為積分增益矩陣。

將上述兩個公式帶入非線性機械系統的動力學模型后，可得出閉環系統的方程如下：

其中B=B0+Kd，通過上述公式，可得知ΔqT TzT為相應系統中唯一靜態平衡點。

根據對傳統線性PID控制的非線性機械系統的分析，可得出相應的定理：

根據非線性機械系統模型定義，傳統線性PID控制系統的應用過程中，通過傳統控制器的比例與微分增益參數適宜的不等式方程的設定和完善，那么系統的位置誤差處于半全局的漸進收斂狀態。也就的存在穩定的吸引域保證

由于公式所表示的Lyapunov函數V保持正定的。并且函數V的值將順著閉環系統實現了時間倒數在平衡點附近內部吸引域的半負定。同時實際上值為零實際上也是Δq的值為零以及q?的值為零。根據LaSalle的不變性原理可了解到，吸引域D的值使處于其吸引域內部的初始值都將漸進穩定實現平衡位置的收斂。這似乎達到了局部漸進穩定的結果，然而實際上影響吸引域大小的常數值沒有出現在非機械系統的控制器中，這個影響的正常數值大小可隨意自定。同時也是吸引域的大小為整體的狀態空間體系，由此，根據相關學者的相似討論可推算出閉環系統的半全局漸進的穩定性特點。

2.2 改進后的非線性PID控制的全局漸近穩定性

根據相應的仿真模擬實驗可知，改善完成之后的NPI-D控制器當中，控制系統中的等價比例的控制參數小于或者等于線性PID的控制參數，非線性機械系統控制器的位置和誤差可根據仿真試驗的結果看出，在通過了初始控制值的誤差暫時狀態過渡完成后，機器人系統位置控制誤差逐漸接近零。同時實現改善后的非線性機械控制系統，也就是NPI-D系統，與傳統的PID控制系統相比具有更快的反應速度。根據推算的理論體系和結論明確到，本論文提出的非線性機械系統NPI-D控制器的改進措施引入了較新的且將小誤差放大的飽和函數，從而明確了在較小的控制增益狀況下依舊能實現較快的過渡過程。為了保證非線性機械系統全局區域穩定性而采取的，通常所用的雙曲余切函數無法放大誤差，為了實現滿意的系統過渡，機械系統中的比例以及積分的增益都相對大一些。

首先通過相類似的勢能函數，實現對相應系統穩定性特點的推導：

針對近似的勢能函數求導可得出非線性的飽和函數如下所示：

通過簡單的運算可證明上述引理的成立。

應用勢能函數針對x求導得出的非線性飽和函數，相應的非線性PI加D的控制器可表述為如下公式：

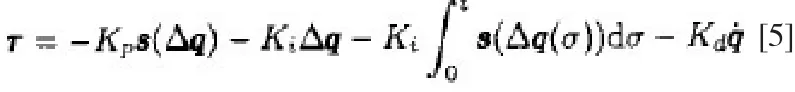
其中的Kp、Kd、Ki的值未恒定對角正定增益矩陣，可是實現如下矢量的定義：

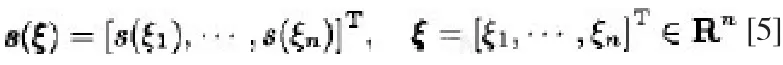
同時引入一定的矢量值：

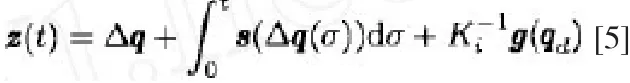
將上述公式代入近似勢能函數可得出閉環的系統方程為：

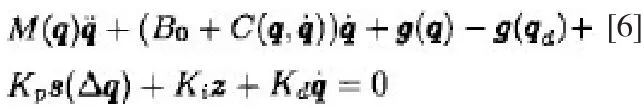
對于公式中所控制的閉環系統，可推出如下定理：

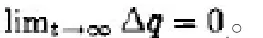
3 結論

通過對相應線性控制的非線性機械系統漸進穩定的分析，清晰明確地回答了這一開放性問題。雖然并沒有對線性控制全局的漸進穩定性進行闡述，但實際證明了實際機械系統中的半全局的漸進穩定性，同時在傳統的線性PID控制半全局漸進穩定性的分析基礎之上，提出了改進的NPI-D控制體系，通過相應專業理論的應用證明了閉環系統呈現全局漸進穩定性，通過實際的實例進一步表明了理論分析結果的正確和有效。

[1]蘇玉鑫，鄭春紅，Peter C.Müller.非線性機械系統PID控制漸近穩定性分析[J].自動化學報，2008(12).

[2]蘇玉鑫，段寶巖.一種新型非線性PID控制器[J].控制與決策，2003(1).

[3]趙國生，魏志綱.基于非線性PID控制的三相有源濾波器[J].鄭州大學學報(工學版)，2005(2).

[4]尚宏，陳志敏，任永平.一種新型非線性PID控制器及其參數設計[J].控制理論與應用，2009(4) .

[5]任廷志，吳忠強.非線性機械系統的模糊保代價控制[J].中國機械工程， 2003(19).

[6]李祖欣，蔣云良.一種新型模糊非線性PID控制器[J].信息與控制，2004(5).