正軸測投影圖直觀效果優化條件的研究

徐越月， 林大鈞

（華東理工大學，上海 200237）

與多面正投影相比，正軸測投影具有立體感強、直觀性好、形象逼真等優點；與透視圖相比，正軸測投影作圖相對容易，度量也較方便；從影像反求角度看，由正軸測投影圖反求物體三維模型也比由照片反求來得容易[1]。

正軸測投影立體感效果取決于平行光束與物體表面所形成的角度大小，其優化指標可根據所表達的對象在正軸測投影中顯示的面的個數以及面積的大小和面積變化率等加以衡量。用面的個數標識正軸測投影表現物體的信息量，用面積的大小標識正軸測投影表現物體的信息量的豐腴程度，用面積的變化率則標識正軸測投影表現物體的變形程度。

1 可見面數的計算方法

當物體進行投影時，立體的每個平面的外法線N矢量與投影方向S之間有一夾角。當夾角大于或等于 9 0°時，表示平面背向投影方向或平行于投影方向，該平面不可見；當夾角小于 9 0°時，表示這個平面向著投影方向，該平面可見。

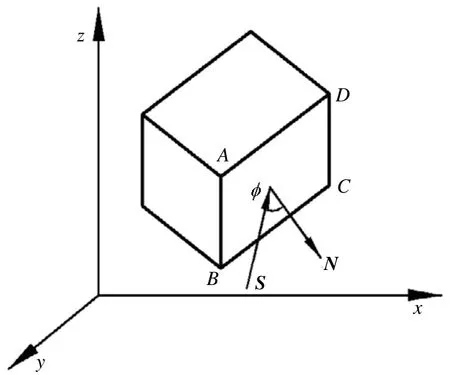
圖1 凸面體表面外法線向量與投影向量關系

如圖 1所示，S為投影方向，N為立體上ABCD面的外法線，沿ABCD面逆時針方向任取相鄰兩邊作為兩個向量AB、BC，這兩個向量的叉積就是該表面的外法線 N的方向，即N = AB × BC。假設A、B、C點的坐標分別為坐標單位向量，可以得到

For i = 1 To NS

U1 = SV(S(i, 2), 1) - SV(S(i, 1), 1)

U2 = SV(S(i, 2), 2) - SV(S(i, 1), 2)

U3 = SV(S(i, 2), 3) - SV(S(i, 1), 3)

V1 = SV(S(i, 3), 1) - SV(S(i, 1), 1)

V2 = SV(S(i, 3), 2) - SV(S(i, 1), 2)

V3 = SV(S(i, 3), 3) - SV(S(i, 1), 3)

N(i, 1) = U2 * V3 - U3 * V2

N(i, 2) = U3 * V1 - U1 * V3

N(i, 3) = U1 * V2 - U2 * V1

If N(i, 2) > 0 Then k = k + 1

Next i

2 可見面積及變化率計算

面積變化率表征著可見面的變形程度，變形過大會導致圖形嚴重失真。正軸測投影視覺上有立體感，但其本質是二維圖形，所以顯示的總面積可以通過每個顯示面的像素和來衡量。在CAD中，正軸測投影圖各點在Z軸方向上坐標皆為0，所以可以通過CAD中的area命令計算其面積，area命令的本質就是求封閉曲線內的像素點之和。

如圖2所示，由于軸測投影圖并不是單一的封閉曲線，CAD具有的功能只是通過在單一的封閉多線段內選取一點來形成面域，這在正軸測投影圖中無法實現，所以先在軸測投影圖周圍設計一個矩形，該矩形輔助邊界比軸測投影圖的最小外圍矩形大一個計量單位，這樣可以使使圖形成為輔助邊界內的孤島。在軸測圖邊框外圍與矩形內側選取一點，使用boundary命令在正軸測投影圖的外圍生成閉合邊界多義線，然后應用(vla-get-area(vlax-ename->vla-object (car(entsel))))語句得到閉合區域的面積，即軸測圖可視面的總面積。

圖2 正軸測投影圖外框示圖

3 程序演示

運行時只需在文本框中輸入旋轉角度α、β，在 CAD中可以得到相應的正軸測投影圖[4]，程序示例如圖3所示。正軸測投影圖的轉換通過lisp編程實現，在程序中加入循環語句，可以大大減少程序的篇幅，具體如下：

(repeat 16

(setq x_set (car (eval(read (strcat "p" (rtos i))))))

(setq y_set (cadr (eval(read (strcat "p" (rtos i))))))

(setq z_set (caddr (eval(read (strcat "p" (rtos i))))))

(setq x_set_change (+ (* x_set S1x) (* y_set S1y) (* z_set S1z)))

(setq z_set_change (+ (* x_set S3x) (* y_set S3y) (* z_set S3z)))

(set (read(strcat "p" (rtos i) "_change")) (list x_set_change z_set_change))

(setq i (1+ i))

)

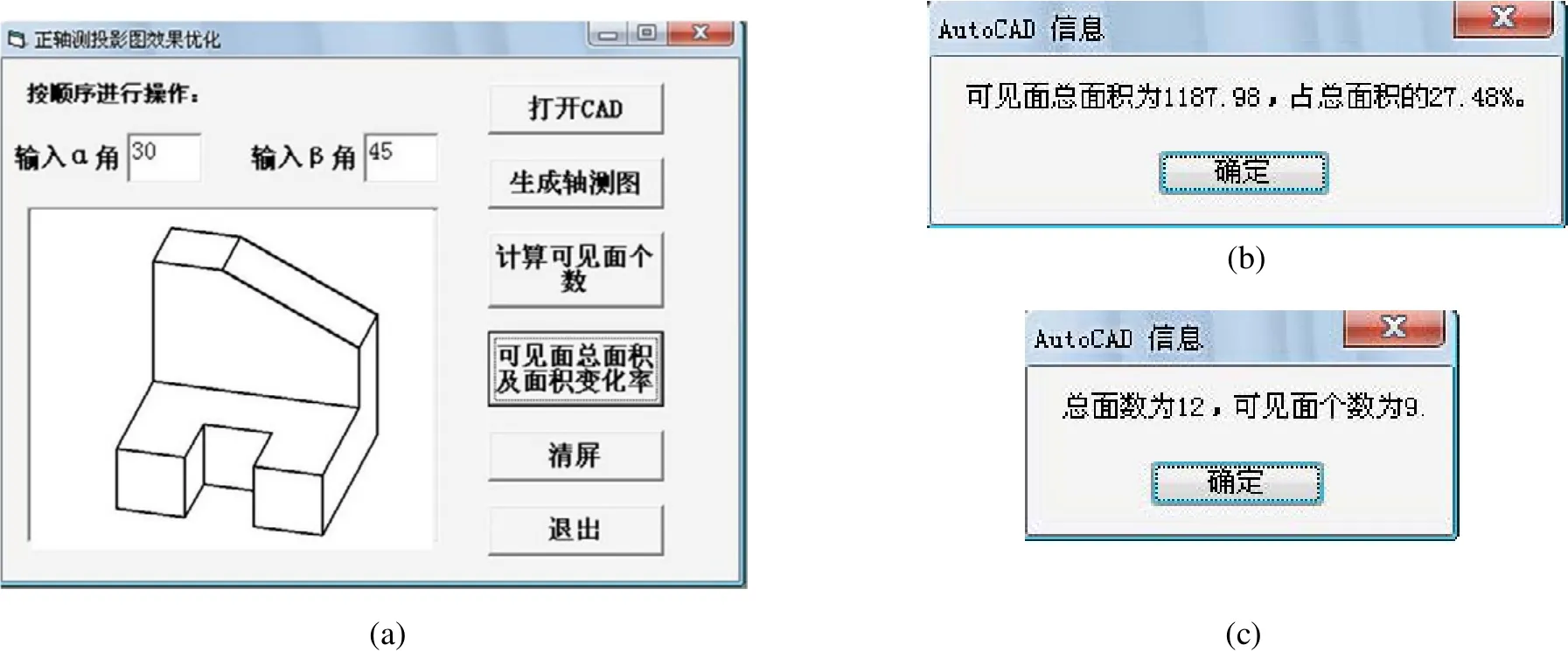
圖3 程序示例

圖2中所示正軸測投影圖通過改變旋轉角度α、β可以得到表1、2中的數據，其中表1反映了旋轉角度α、β與可見面個數之間的關系，表2反映了旋轉角度α、β與可見面變化率之間的關系。

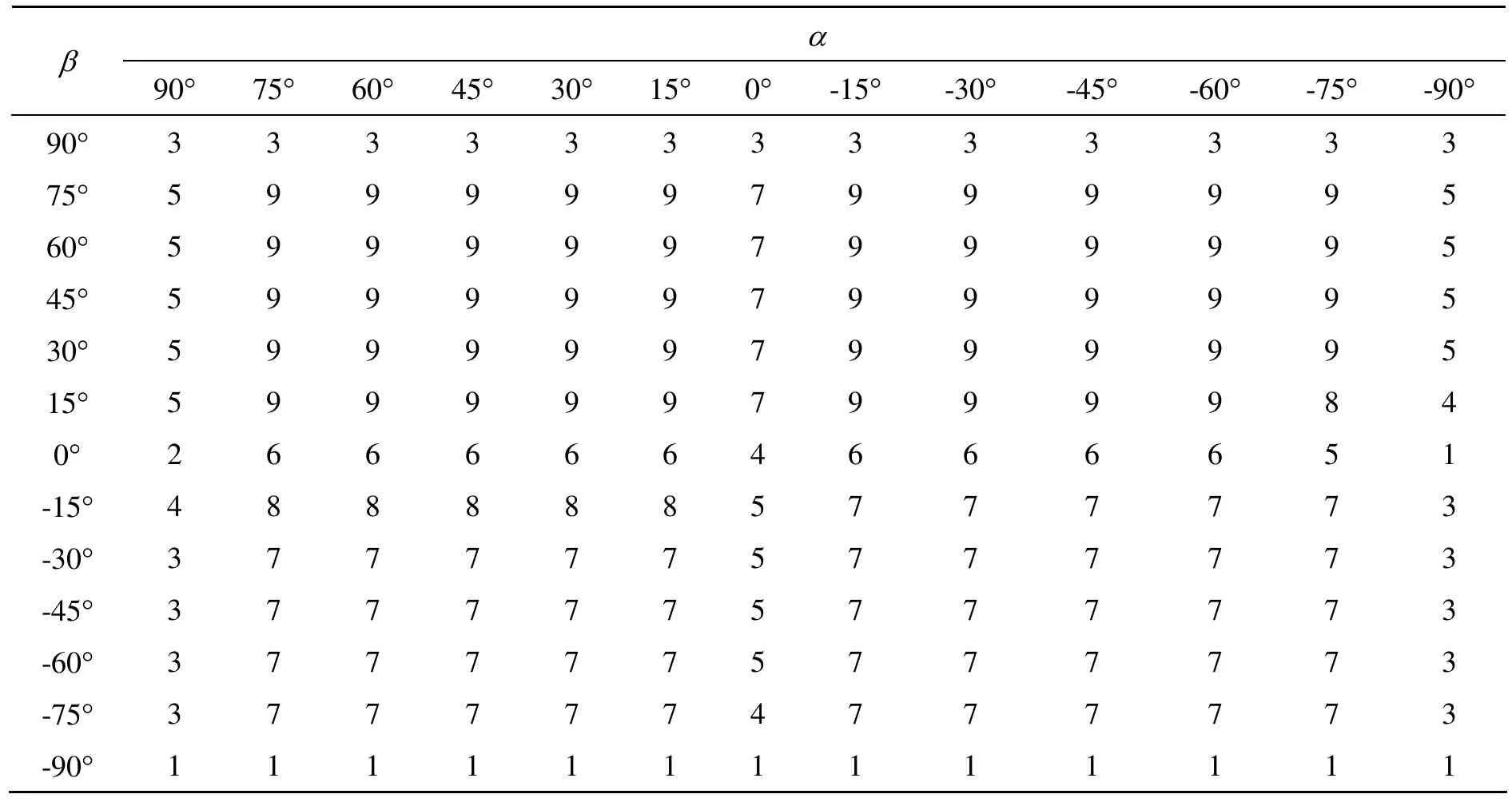
表1 旋轉角度與可見面之間個數的關系

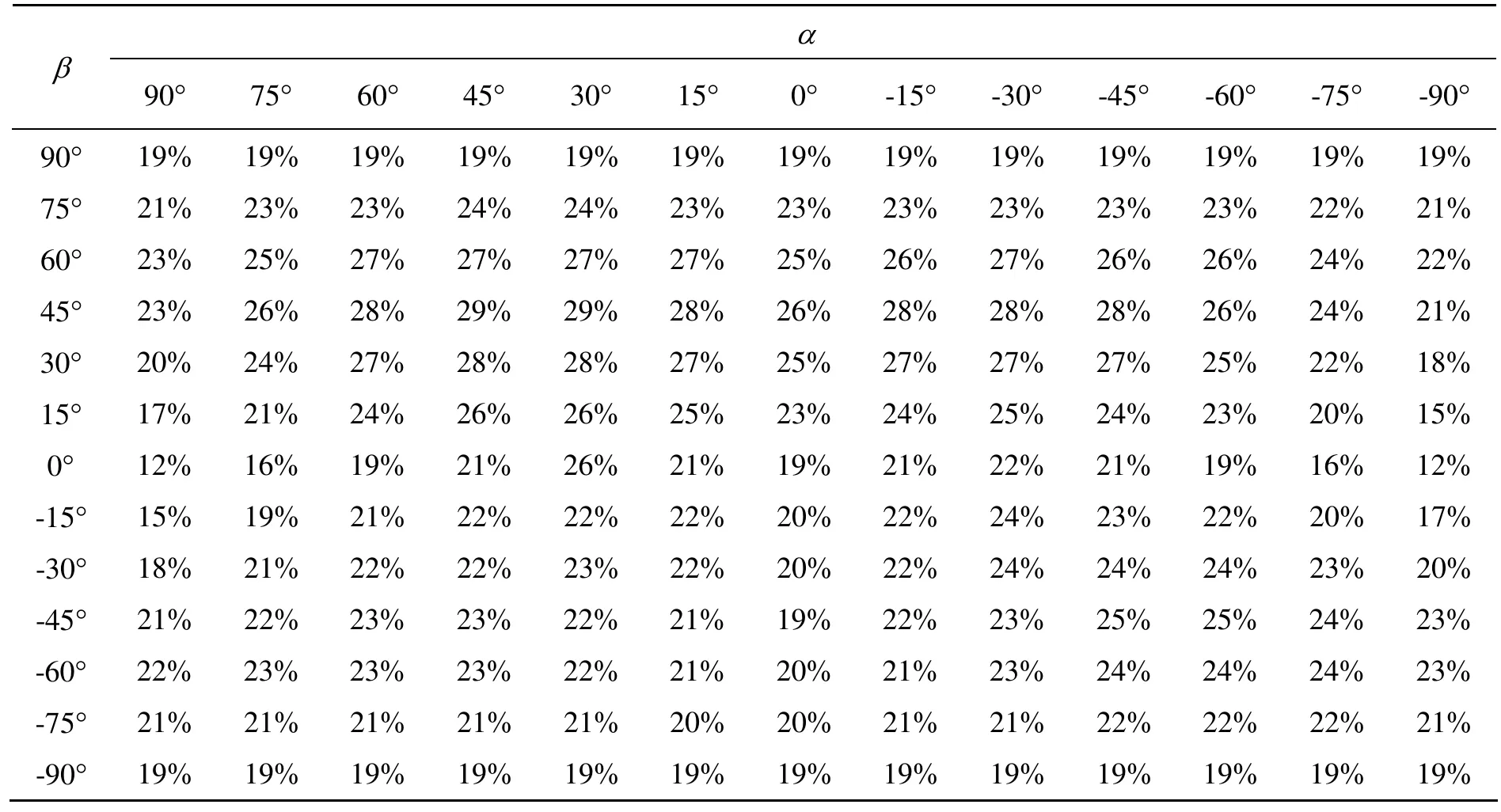
表2 旋轉角度與可見面面積變化率的關系

4 優化條件

面的個數、面積大小、面積變化率三者之間是相互抑制的，其中一個因素的變化可能會使另一個因素隨之而變化，所以要在三者之間取得平衡，即圖形的最佳表達方式。

要獲得較好的直觀效果，首先應避免面投影成線、線投影成點的現象[5]，圖 4(a)的直觀性就很差，同時應盡量使幾何體的內部裸露出來，圖4(b)應改變β角使凹槽面向視點。實驗表明，合適的視角會使得對象顯示面的數目較多，從而使反映的物體信息量更加豐裕，比較圖4(c)與圖2，可以看出圖2的直觀效果較好。由表1、2可以看出，當α、β在30°～60°之間時，顯示面個數較多，且面積變化率百分比較大，同時各面大小比例比較均勻，這樣更加符合人的視覺習慣。

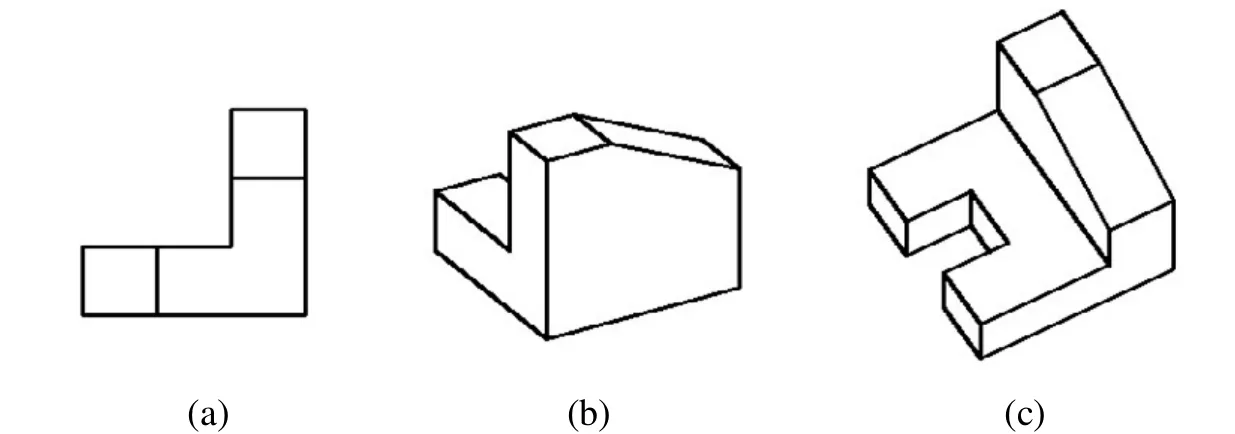
圖4 圖形示例

5 小 結

文章研究的是在已知投影角度的情況下，計算其投影面個數、大小以及變化率。根據研究結果可知工程上常用的基本視圖是正軸測投影圖的特殊情況，利用基本視圖獲得物體表面積計算比較繁瑣，而利用正軸測投影圖計算表面積則比較方便，可為計算物體表面積涂料用量、加工面積大小提供依據。

[1]韓素蘭, 程 方. 常用軸測投影圖在工程中的選擇與應用[J]. 華北水利水電學院學報, 2005, 26: (4):76-78.

[2]陳錦昌. VB計算機繪圖教程[M]. 廣州: 華南理工大學出版社, 2003: 99-103.

[3]張晉西. Visual Basic.Net二次開發AutoCAD范例精解[M]. 北京: 清華大學出版社, 2004: 3-16.

[4]林大鈞. 計算機工程圖形算法及應用[M]. 上海: 華東理工大學出版社, 2006: 111-115.

[5]牛中原, 遲秋影. 理想正軸測投影作法[J]. 佳木斯大學學報(自然科學版), 2002, 20(4): 461-463.