基于黎曼度量參數曲面四邊形網格生成方法及UG實現

郭新強， 張見明， 覃先云， 穆東輝， 宋 喬

（1. 湖南大學汽車車身先進設計制造國家重點實驗室，湖南 長沙 410082；2. 北京第二機床廠有限公司，北京 100072）

曲面網格生成的方法通常分為直接法和映射法[1]。直接法是指曲面網格的劃分直接在曲面的物理空間進行；映射法是首先利用平面域網格生成方法在曲面的二維參數空間進行網格剖分，然后將剖分結果映射到三維物理空間形成曲面網格。本文利用反映曲面扭曲程度的黎曼度量[2-4]，將用于生成平面四邊形網格技術的鋪磚法[5]擴展運用于任意復雜曲面的網格生成。鋪磚法首先由Blacker T D和 Stephenson M B提出的，該法具有較高的邊界靈敏度，可以較好的擬合網格區域復雜的邊界形狀，能生成質量較高的網格。在原有的鋪磚法中，首先沿著網格邊界生成一排單元，然后再考慮相交情況，使得相交處理復雜。在本文實現該方法過程中，每生成一個單元時就預先判斷相交情況，根據判斷對相交單元做簡單的處理，省去了原方法中對多次相交優先處理環節，從而使得整個的相交處理變得簡單。

本文利用改進的鋪磚法生成的四邊形單元是用于一種新的結構分析算法——邊界面法[6]前處理的二維參數曲面網格。邊界面法由張見明等人最近提出，該法直接利用CAD實體模型的邊界參數曲面信息在二維參數空間中劃分網格并在曲面的二維參數空間內進行邊界積分和變量插值。在數值積分過程中，積分點的幾何數據直接由參數曲面的參數變量計算得到[7]，而不是基于單元由多項式插值近似的，避免了幾何誤差。該方法中所使用的四邊形單元定義在曲面的二維參數空間，而不是像有限元法中的單元定義在三維物理空間。有限元法的幾何模型是通過單元插值近似的，當網格較稀疏時具有明顯的幾何誤差。邊界面法是利用二維參數空間的值進行數值計算，現有的有限元前處理商業軟件能輸出模型的三維物理空間坐標，但必須再經過計算才能獲得二維參數空間的值。因此，該類單元不能從現有的有限元法前處理的商業軟件中直接得到。為了保證良好的積分和插值精度，一般要求二維參數單元在對應的三維物理空間中的網格具有良好的形狀。為此，作者將鋪磚法運用到任意復雜曲面生成參數曲面網格，實現邊界面法的前處理。

UG是一款采用全參數化建模CAD軟件，并提供了強大的二次開發工具UG/Open[8]。本文通過VC++編程調用UG/Open庫函數獲取CAD模型的曲面參數信息。在參數域內利用改進的鋪磚法生成網格，然后將二維參數域上生成的網格映射到曲面的三維物理空間，從而生成曲面的最終網格。為了使二維參數域上生成的網格投到曲面的三維物理空間保持較好的質量，本文在參數域上生成網格時運用黎曼度量方法對網格的形狀和大小進行控制。文章最后給出了4個算例驗證了算法的可靠性，并且說明了不論是在平面還是曲面上都能生成質量較好的四邊形網格。

1 黎曼度量

曲面二維參數域上的點與三維物理空間的點是一一對應的關系。對于簡單的曲面直接映射法能生成質量較高的網格，對于曲率變化劇烈的曲面，由于其映射函數在參數域的兩個方向的非線性生成的網格的質量往往較差。為了使二維參數域上生成的網格投影到曲面的三維物理空間保持較好的質量，采用黎曼度量的方法可以控制網格形狀和大小。

1.1 參數曲面的黎曼度量

三維空間的一個參數曲面S與二維參數空間的一一對應關系可用函數表示為

在UG二次開發環境中，只需知道二維參數域中每個節點u和v兩個參數值就可以調用的庫函數UF_MODL_evaluate_face（…）獲得節點沿參數u和v的切向量Su和Sv，進而得到參數曲面黎曼度量矩陣。

1.2 參數線段弧長計算

參數域內線段兩端點為 P1和 P2，則該線段上任意點可表示為 P = P1+ ( P2- P1)? t ，0≤t≤1。P點的黎曼度量可表示為

考慮黎曼度量后線段上兩點A和B的在三維物理空間長度可以用下面公式計算[2]

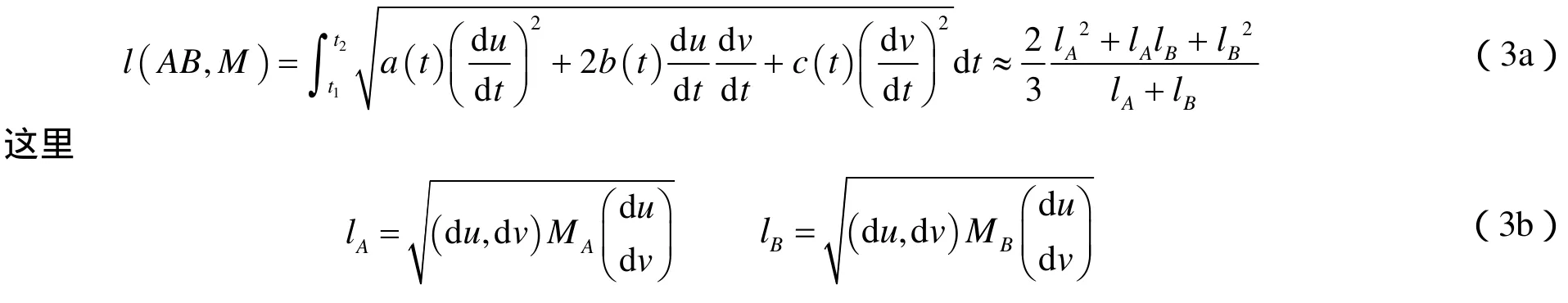
當曲線上兩點A( t1)，B( t2)的度量矩陣特征值變化不大時可用上式，否則需要把線段分成若干段，計算每小段li的長度，總長度為

1.3 參數向量的旋轉

二維參數空間中向量AB需逆時針旋轉一個角度后得到新的向量AC，則向量AC由下式計算得到[3-4]

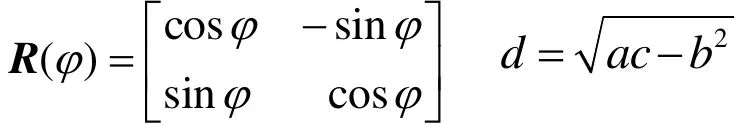
lAB為向量AB在三維物理空間的長度，可根據參數弧長計算公式(3a)或者式(3c)得到，lideal為生成C點所需的三維物理空間理想長度，φ根據前沿DA和AB映射到三維物理空間中形成的角度∠DAB而確定。如圖1(a)圖1(b)，沿AB逆時針方AB逆時針方向φ為的度量矩陣，根據公式(4)即可求出向量AC，點A為已知點，則可以求出C點在二維參數空間的值。

圖1 向量旋轉角度

2 曲面參數空間四邊形生成

2.1 網格生成過程

根據鋪磚法的一般原理，如圖2給出了生成曲面網格的整個流程。本文對相交處理做了改進，并且在2.2做了詳細的闡述，其它過程只簡單介紹，其細節可以參考文獻[5, 9-10]。

1）邊界離散

調用UG庫函數獲得實體表面的參數域，對參數域的邊界進行離散。內邊界點按順時針方向連接，外邊界點按逆時針方向，且保證離散點數為偶數。

2）節點分類及最優邊選擇

節點內角是指節點Ni與其所在邊界上前一節點Ni-1和后一節點Ni+1投到三維物理空間的角度。根據節點內角的不同分為 4種類型：(1) 終 止 節 點 α≤ 1 35°；(2) 邊 節 點135°＜ α ≤ 2 25°；(3) 角節點225° ＜ α ≤ 3 00°；(4)轉節點300° ＜ α ≤ 3 60°。

如果Ni為終止節點則邊界 NiNi+1為最優邊開始生成單元，每次選取前沿邊界中的一條邊作為基邊生成四邊形。

3）生成新單元及相交判斷

本文中單元是在二維參數域中生成的。每次生成一個新的單元是根據基邊兩個端點的節點內角在參數域中生成新的節點，從而生成新的單元。新節點的位置可根據公式(4)確定，其中 lAB為基邊在三維域中長度，lideal的長度可以參考文獻[5, 9-10]中計算新節點的向量長度，MA是節點的度量矩陣。形成單元后，新邊要判斷是否與前沿邊界相交，如果相交就進行處理，在下節中詳細介紹相交處理過程。

4）生成一排單元及邊界調整

以終止節點作為新生單元的起點，如果沒有終止節點選擇最小節點內角作為起點，直到再次遇到終止節點完成一排單元的生成，當所有的活動前沿邊界都作為基邊生成單元后就完成一層單元的生成，然后更新活動前沿邊界。一層單元生成后，如果更新的活動前沿邊界尺寸有變大或者縮小的趨勢則進行單元楔入或者刪除單元操作，具體過程參考文獻[5, 9-10]。

5）光滑處理和縫合處理

為了使生成的邊界尺寸大小均勻，以及邊的垂直度，可以對更新的前沿邊界節點進行邊界光滑，內部節點進行內部光滑。如果尺寸過渡比較大或者出現內角很小的情況可以進行縫合處理，詳細情況可以參考文獻[5, 9-10]。

6）閉合處理及優化網格

當前沿邊界節點數目小于等于4時就進行封閉處理，整個區域網格生成完成。用改進的鋪路法完成全四邊形網格生成后，每個節點最理想的是由4個單元共用，這樣形成的四邊形較規則。如果每個節點由3～5個單元共用，生成的單元是符合要求的。由于幾何邊界的復雜性和網格尺寸不均勻常常導致局部網格形狀不好，所以需進一步優化。優化后需再對除幾何邊界節點外節點用內部節點光滑方法進行幾次迭代光滑，保證生成的網格質量更好。

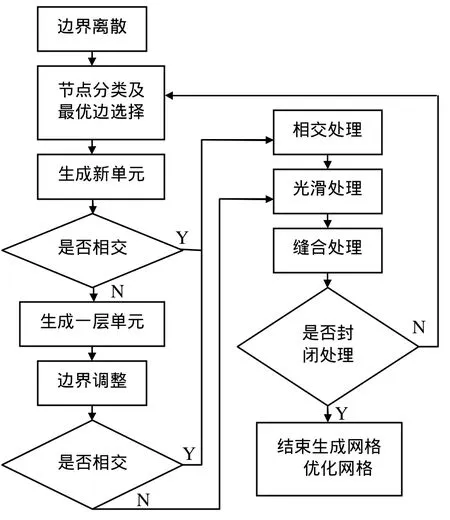
圖2 程序流程

2.2 相交處理

原有的鋪磚法網格是逐排生成的，生成一排單元后再去處理相交問題。如果采用這種方法處理，特別是出現多次相交還要進行優先處理判斷，這樣使程序比較復雜。本文對相交處理過程做了改進，采用生成一個單元時就進行相交判斷，如果遇到相交就進行相交處理。

經過改進后的相交處理過程可分為 3個部分：

1）優先處理新單元中相交線段新生成的點；

2）如果1）未完成處理則處理新單元中相交線段原有節點；

3）如果前兩步都未處理好，則搜索基邊節點附近的點，如果滿足要求則替代新節點，如果沒有滿足要求的點則取消此單元生成，并以相鄰邊作為基邊生成單元。

如圖 3所示，新生成的單元邊 NiNi+1和NiNi-1與前沿ab相交，Ni為新生成的點，相交處理后必須保證邊界形成環后的節點數為偶數，圖3中是兩個環合并為一個環，Ni點距離b點近所以選b作為替代的點，圖3(c)所示。點Ni被點b替代后根據點b兩邊的角度來確定邊的合并，如圖3(d)所示為合并邊后的結果。

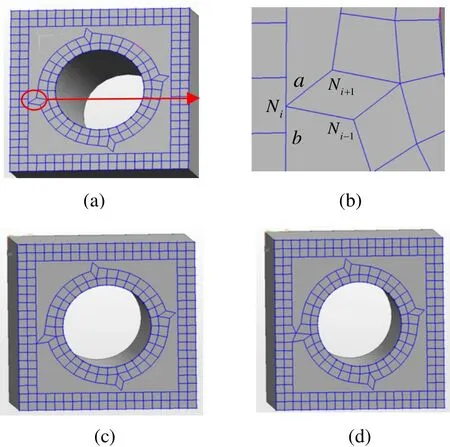
圖3 新節點相交處理

如圖4所示，圖4(a)中直線未相交，此時以邊NiNi-1作為基邊生成四邊形，生成新節點Nj并生成四邊形，圖4(b)圖所示，新生成的單元邊Ni+1Nj與前沿ab相交，如果新節點由節點a替代形成的邊界環不滿足偶數個節點要求，如果新節點由節點b替代生成的邊還是與前沿相交，此時考慮節點 Ni+1由a或者b替代。在本例中由a替代，如圖4(c)所示。縫合最終生成的圖形如圖4(d)所示。

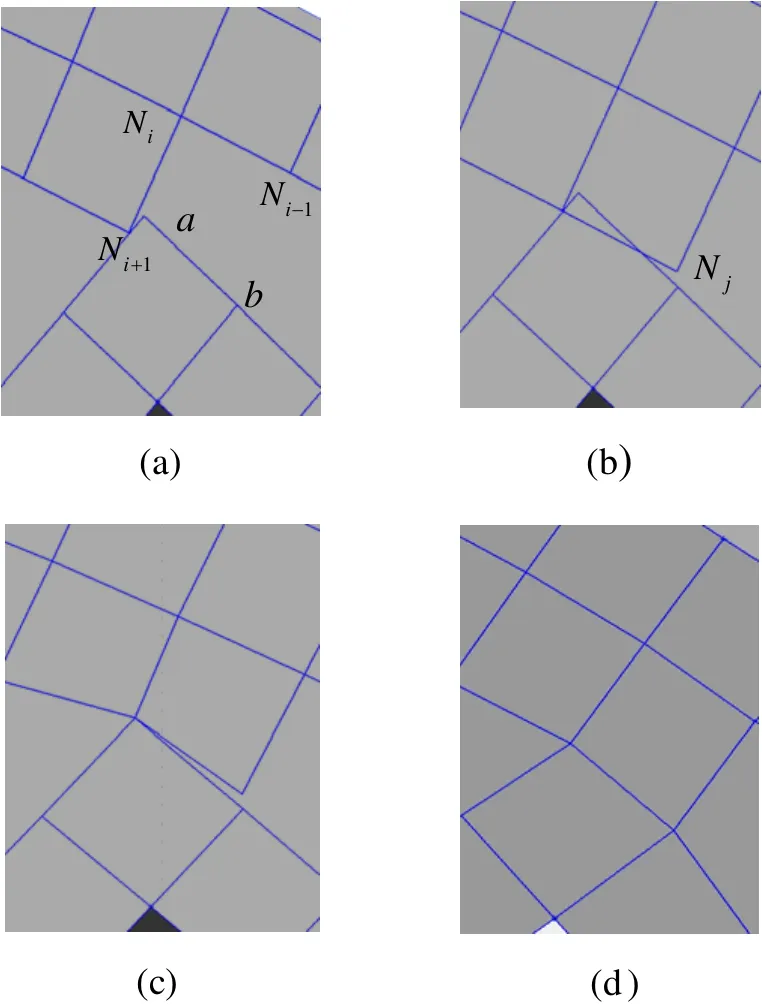
圖4 原節點相交處理

如果以上兩個處理過程都不能生成單元，則進行第3步處理。如圖5所示，邊界AB為基邊，根據節點B的節點內角生成C點，假設C點按前面兩步都不能處理相交問題，則以B為中心在參數空間建立一個搜索區域，在區域內尋找最優的點。

首先確定在三維空間的搜索半徑r3D，一般取邊界AB在三維空間長度的兩倍。考慮度量矩陣，以搜索半徑r3D構成的區域在參數空間里為一橢圓，參數橢圓的中心在B點。因此，要計算參數橢圓的長半徑和短半徑，以確定簡單的參數矩形。根據搜索半徑r3D，由以下公式計算對應的參數半徑

方程(5)等價于中心在圓點極坐標中的橢圓方程，能轉化為參數坐標下橢圓形式的方程為

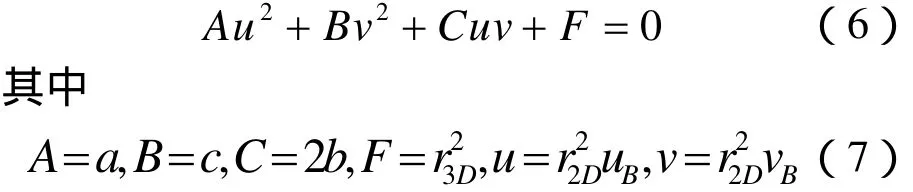
通過旋轉橢圓與坐標軸平行，方程(6)可以簡化，得到橢圓在參數空間的長短半徑分別定義為

得到橢圓的長短半徑后，可以簡單地在參數空間里確定矩形搜索區域，如圖4所示的矩形框。搜索區域建立好后選擇最優點，如圖6所示，前沿節點P1, P2, P3為搜索區域內的點，最優點形成四邊形后要保證每個邊界前沿節點數目為偶數個，圖中P2不滿足要求，P1和P3滿足奇偶性要求，本文中選取∠APB張角最大的點，即P1是最優點。

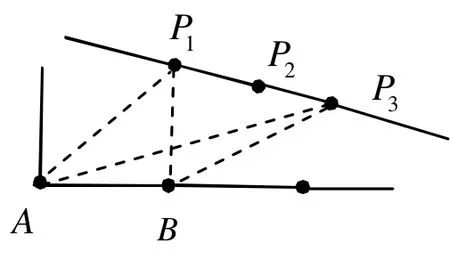
圖6 選擇最優點

3 四邊形質量評價因子

網格質量的好壞將影響計算精度，本文采用幾何準則對四邊形網格進行質量評價。如圖7所示四邊形ABCD的兩條對角線將其分為4個三角形△ABC，△ABD，△CDB，△CDA，通過計算這4個三角形的質量因子得出該四邊形的質量因子。

圖7 分割四邊形

三角形ABC的質量α因子[11]定義如下

n是三角形的單位法向量，α的意義就是三角形面積與變長的平方和之比，0＜α≤1，α越大三角形質量越好。令4個三角形△ABC，△ABD，△CDB，△CDA的α因子分別為1α，2α，3α，四邊形β因子[12]定義為

0＜β≤1，β越大四邊形質量越好，根據文獻[11]中β不同的范圍來評價四邊形質量，如表1所示。

表1 四邊形 β 評價因子[11]

4 UG實現過程

本文利用VC2005編程平臺通過External連接方式實現UG二次開發。首先，在VC2005環境里建立一個動態(.dll)項目。然后，對項目進行設置即可與 UG/Open API建立連接關系。在VC2005編譯環境里對VC++項目的設置為：

1）菜單選項-工具選項項目和解決方案VC++目錄：

在“庫文件”和“包含文件”里添加UG安裝目錄下的UGSNX 4.0UGOPEN

2）菜單選項-項目屬性頁連接器輸入附加依賴項：

添 UG Open 的庫文件名 libufun. lib,libugopenint. lib和libnxopencpp.lib。

3）菜單選項-項目屬性頁連接器常規輸出文件：

添加‥startup$(ProjectName).dll。

4）菜單選項-項目屬性頁配置屬性常規字符集：

下拉選項中選擇為“使用多字節字符集”。

通過上面的設置，VC++環境里的項目與UG/Open建立了聯系，成功編譯項目后就在該項目目錄下的startup文件中生成相應可以在UG中執行的.dll文件。在 UG環境里利用菜單工具——調用.dll就可以在相應的曲面上生成網格。

當與 UG/Open建立聯系后可以調用其中的庫函數獲取實體模型的曲面信息，根據獲得的曲面參數空間進行邊界離散，并運用第2節中的網格生成方法在參數空間生成網格，并映射到三維物理空間。

下面給出在 UG/Open API中常訪問和生成幾何的函數以及功能：

UF_MODL_ask_body_faces(…)：獲得實體的所有曲面；

UF_MODL_ask_face_edges(…)：獲得曲面的所有邊界曲線；

UF_MODL_ask_face_uv_minmax(…)：獲得曲面的參數范圍；

UF_MODL_evaluate_face（…）：獲得節點沿參數u和v的切向量以及節點映射到三維物理空間的坐標；

UF_POINT_create_on_surface(…)：在曲面上生成點；

UF_CURVE_create_line(…)：生成線段；

UF_OBJ_set_color(…)：生成的網格在物理空間的顏色顯示。

5 網格生成實例

該節給出了利用本文算法生成曲面四邊形網格實例，如圖8～圖11所示。網格單元直接在UG環境中的CAD模型表面生成，保持了模型的原始幾何信息。根據網格質量因子對各種實例的網格質量進行了評價，其結果如表2所示。可以看出基于黎曼度量改進后的鋪磚法無論在平面還是曲率大的曲面都可以獲得質量較好的網格。

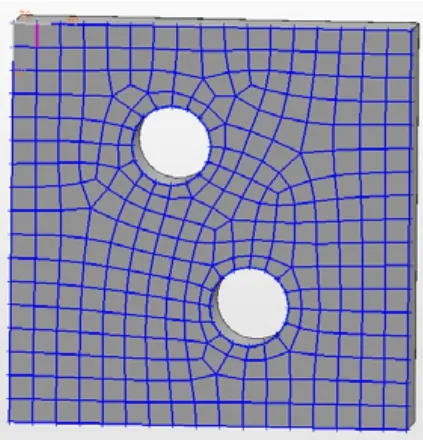
圖8 實例1

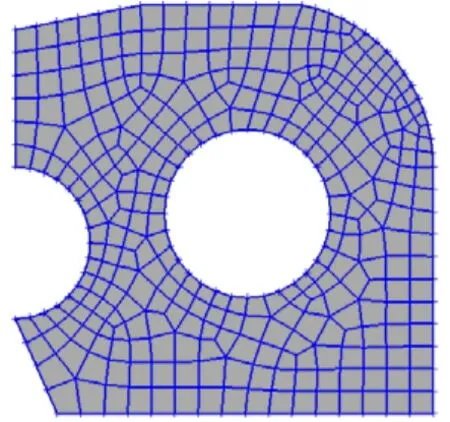
圖9 實例2

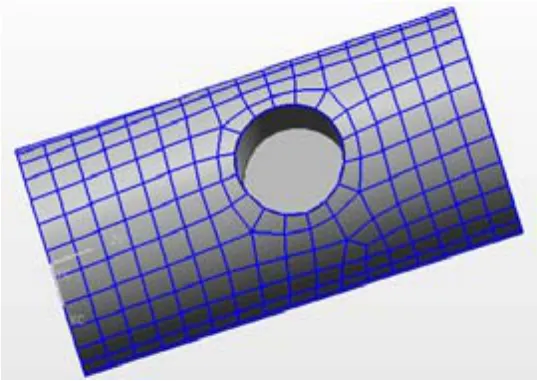
圖10 實例3

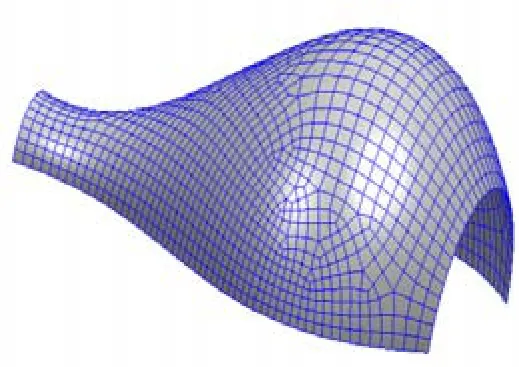
圖11 實例4

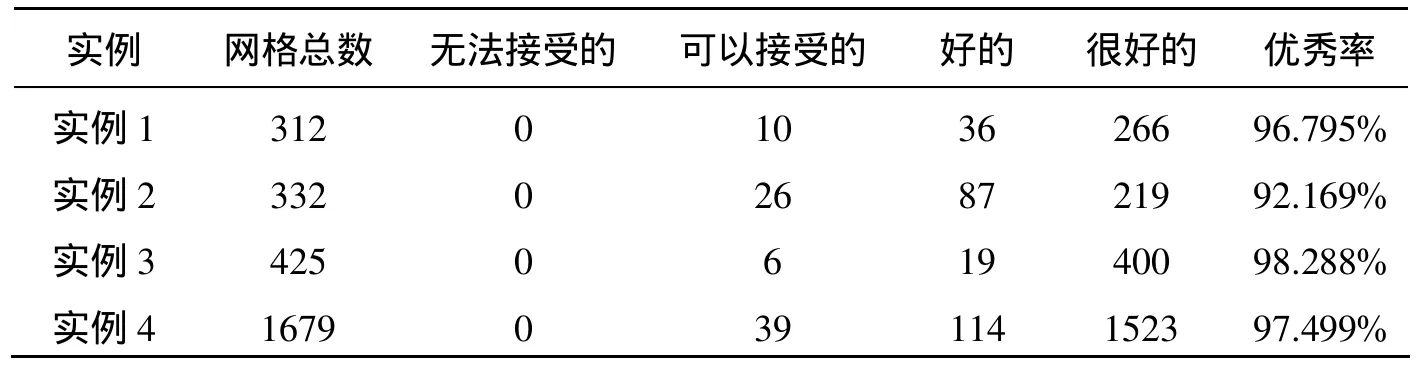
表2 實例質量評價表

6 結束語

本文基于黎曼度量將鋪磚法擴展運用到任意曲面的四邊形網格生成，并在原有算法的基礎上對相交處理過程做了改進，使得相交處理更加簡單有效。基于UG二次開發工具，利用VC2005平臺在UG建模環境中實現了曲面的二維參數空間網格劃分，且網格單元在三維空間質量較好。在網格生成過程中，調用UG Open/API中相應的庫函數，獲取CAD實體邊界曲面參數信息，并將最終生成的網格顯示在實體表面。后續的工作是將這種參數四邊形網格應用到邊界面法中作為前處理網格。邊界面法與CAD無縫連接能避免幾何誤差，提高計算精度，實現CAD與CAE的無縫連接，對數值計算有非常重要的意義。

[1]張建華, 葉尚輝. 有限元網格自動生成典型方法及發展方向[J]. 計算機輔助設計與制造, 1996, (2):28-31.

[2]關振群, 單菊林, 顧元憲. 基于黎曼度量的復雜參數曲面有限元網格生成方法[J]. 計算機學報, 2006,29(10): 1823-1833.

[3]Lee C K. Automatic mesh generation using metric advancing front approach [J]. Engineering Computations, 1999, (16): 230-263.

[4]Lee C K. Automatic adaptive metric advancing front triangulation over curved surfaces [J]. Engineering Computations, 2000, 17: 48-74.

[5]Blacker T D, Stephenson M B. Paving: a new approach to automated quadrilateral mesh generation [J].Numer. Meth. Engrg, 1991, 32: 811-847.

[6]Zhang Jianming, Qin Xianyun, Xu Han, et al. A boundary face method for potential problems in three dimensions [J]. Numer. Meth. Engrg, 2009, 80:320-337.

[7]覃先云. 基于參數曲面的邊界面法研究[D]. 長沙:湖南大學, 2009.

[8]侯永濤, 丁向陽. UG/Open 二次開發與實例精解[M].北京: 化學工業出版社, 2002: 1-2.

[9]張清萍, 尚 勇, 趙國群. 二維全四邊形網格的自動生成算法[J]. 山東大學學報, 2002, 32(3):254-259.

[10]林勝良, 方 興, 張 武, 等. 一種改進的高品質全四邊形網格生成方法[J]. 江南大學學報, 2006,5(1): 70-73.

[11]Lee C K, Lo S H. A new scheme for the generation of a graded quadrilateral mesh [J]. Computers and Structures, 1994, 52: 847-857.