干涉儀測向技術研究＊

羅賢欣 劉光斌 王 忠

（第二炮兵工程大學 西安 710025）

1 引言

干涉儀測向的實質是利用無線電波在測向基線上形成的相位差來確定來波方向。干涉儀測向技術自出現以來，因其測向精度高、靈敏度高、結構簡單、原理清晰、觀測頻帶寬等優點在電磁環境監測、電子對抗、雷達、聲納、導航等領域得到了廣泛應用。干涉儀測向性能主要是通過解相位差模糊和天線配置形式、鑒相準確度、通道幅相校正技術、數據處理方法四個方面來進行改進和提升的［1］。本文著重對相位差模糊和天線配置形式進行考慮，優化選擇實現方法來滿足測向性能要求。

2 一維相位干涉儀

2.1 一維單基線干涉儀測向原理

“一維”是指測向天線為“線型”布陣，即所有的測向天線陣元都處于同一條直線上，與之相對應，“二維”是指測向天線為“面型”布陣，即所有的測向天線陣元都處于同一個平面［2］。

如圖1，單基線干涉儀由兩個信道組成，兩個接收天線之間的距離d，輻射源與天線軸線夾角為θ，則電磁波到達兩天線的行程差ΔR＝dsinθ，雷達信號的波長為λ，相應兩天線輸出信號之間的相位差φAB：

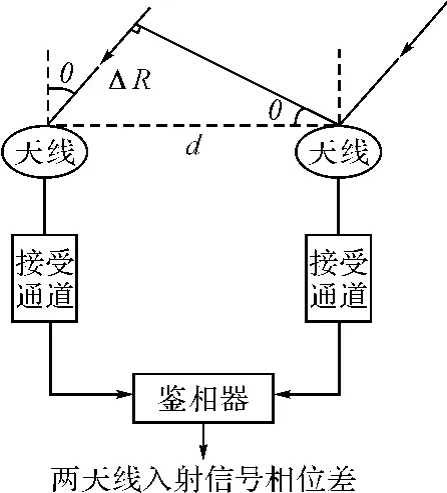
圖1 一維單基線干涉儀測向原理圖

理論上講，如果兩天線后的接收通道完全一致，則加到鑒相器時兩信號的相位差還是φAB。在已知雷達信號頻率f時，利用鑒相器測出相位差φAB后就可測出信號方位角θ：

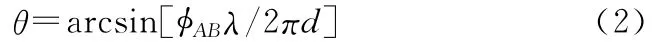
從公式可以看出要想提高測向精度：

1）入射角越小越好；

2）相位誤差越小越好；

3）頻率越高越好；

4）基線長度越長越好。

入射角和頻率是相對固定的，鑒相器鑒相誤差不能任意減小，最為容易控制的是基線長度，所以要提高測角精度就要盡可能的增加基線的長度。

另一方面，由于兩天線之間的相位差φ是入射角θ的周期函數，即：φ＝（2πd／λ）·sinθ，如果d、λ兩參數已定時，若θ的變化范圍過大超過2π，使得鑒相器輸出的相位差φ′不等于φ，即：φ′＝φ±2kπ（k為某一正整數），從而出現“相位模糊”，不能分辨雷達信號的真正方向。不模糊視角θm：

可見，要擴大干涉儀的視角，必須減小兩天線之間的距離d。由于測向精度和測向范圍兩個指標對基線長度d的要求正好相反，因此單基線相位干涉儀不能解決測角精度和測向范圍之間的矛盾。

2.2 一維多基線干涉儀測向原理

為了解相位模糊，一般采用長短基線結合的辦法：利用多天線組陣構建的多基線干涉儀系統，由較短間距的干涉儀來確定覆蓋寬視角，較長間距的干涉儀決定測角精度［3～6］。

一維多基線干涉儀，就是長短基線法在一維干涉儀中的應用。如圖2，假設入射波方向與天線軸線夾角為θ，波長為λ；A0、A1、A2是天線陣元，A0與A1的基線長度為d1（d1＜λ／2），A0與A2的基線長度為d2（d2＞λ／2且d2＝nd1，其中n＞1）；A0與A1的基線相位差測量值是Ψ1，A0與A2基線相位差測量值是Ψ2；入射波實際到達陣元A0與A1的相位差是φ01，入射波實際到達陣元A0與A2的相位差是φ02，A0與A2基線相位差的粗值是φ02′，理想情況下有：

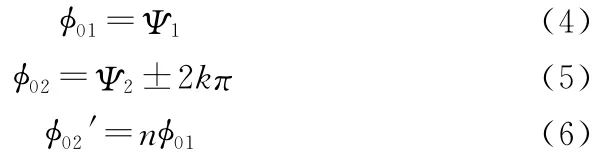
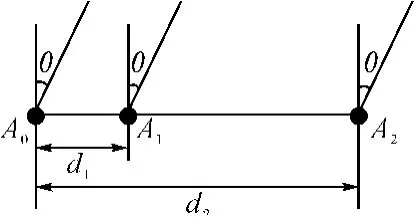
圖2 一維多基線干涉儀示意圖

聯立以上三個方程便可求出較為精確的測向結果。

該方法是以長基線測量值為基礎，推算出長基線實際相位差值的粗值，然后用短基線測量值和長短基線幾何長度的比值確定長基線相位差實際值的范圍，進一步從若干個可能中確定精確值。長短基線組合的干涉儀，用短基線 “解模糊”，長基線保證精度，可以巧妙地把短基線的唯一性和長基線的測量精確性結合起來。

3 二維干涉儀測向原理

3.1 二維單基線干涉儀測向原理

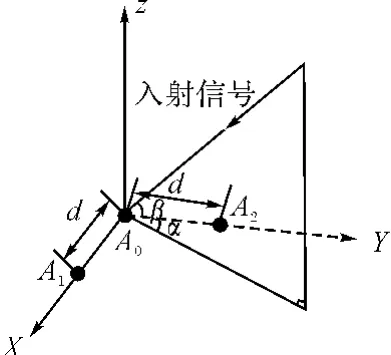
圖3 二維單基線干涉儀測向原理圖

為了便于理解二維干涉儀測向原理，先從二維單基線干涉儀測向原理進行分析。如圖3所示，在直角坐標系XYZ中，以直角三角形頂點布陣等長基線的三元陣為例，陣元A0與A1，A0與A2的基線長度都為d。假設α為入射信號方位角，β為入射信號仰角，λ為來波波長，Ψ1為陣元A0與A1基線相位差，Ψ2為陣元A0與A2基線相位差，則有：

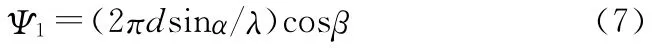
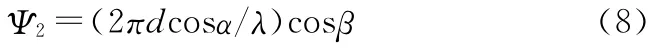
由公式（7）和（8）可以解出入射方位角α和入射仰角β：

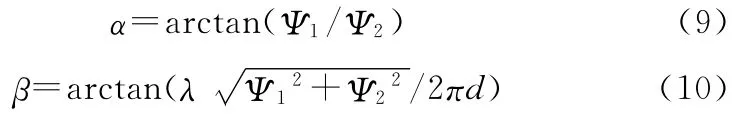
3.2 五單元圓陣干涉儀測向原理

二維多基線相位干涉儀測向原理以五單元圓陣干涉儀［7］為例進行分析。如圖4，在直角坐標系XYZ中，圓陣位于XY平面內，五個天線陣元均勻分布于1－5點。入射方向二維角度為（α，β），α為入射方向與X軸夾角，β為入射方向與Z軸夾角。為提高測向精度，采用長基線形成的相位差進行測向。

假設相鄰兩陣元的夾角ω＝2π／5，陣元1與X軸的夾角γ＝π／2－2π／5，陣元1－3，2－4，3－5，4－1，5－2的基線相位差分別是Ψ13、Ψ24、Ψ35、Ψ41、Ψ52，則可利用陣元長基線相位差信號模型如下：

利用其中兩條基線的相位差組合即可進行二維測向，以Ψ13、Ψ24為例進行測向原理說明：對Ψ13、Ψ24分別求和差：

對式（16）除以 －8π／λγsinωcos（w／2），得到剩余項：sinβsin（α－γ－3ω／2）；

對式（17）除以－8π／λγsinωsin（w／2），剩余項為sinβcos（α－γ－3ω／2）。

由上面兩個剩余項構造復數：

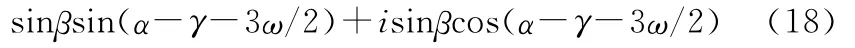
對式（18）乘以exp［－j（γ＋3w／2）］，可以得到新的復數：f＝sinβsinα＋isinβ，結合式（16）、（17）可得出二維入射角估計：

圖4 五元圓陣干涉儀原理圖

3.3 二維陣相位干涉儀與一維相位干涉儀之比較

一維相位干涉儀結構緊湊，原理簡單，長短基線干涉儀只要求短基線長度小于半波長，但使用的場合也相應受到限制：一維相位干涉儀無法區分前方與后方，測向的測向方位角范圍只能為±90°；不適合以下來波有仰角的測向場合（機載測向、地對空目標測向、短波天波測向），否則會引起額外的測向誤差。

二維相位干涉儀同一維相位干涉儀相比具有以下優點：

1）二維相位干涉儀可360°全方位測向；

2）二維相位干涉儀布陣形式靈活，常用的布陣形式是采用圓陣布置，采用圓陣的好處是天線陣元位置相互對稱，易于實現測向校正；

3）二維多基線干涉儀天線陣單元間距不受小于半個工作波長的約束：利用多個天線對的測向值進行數據處理，可得較精確的測向值；

（4）二維相位干涉儀可以同時測方位角與仰角，不存在因仰角引起的相位模糊。

4 基于長短基線圓陣布置干涉儀

高頻信號的波長很短，利用長、短基線相結合的方法解相位模糊，此時天線陣元必須做得非常小，這將降低天線增益并造成天線互耦，同時過小的短基線長度會增加系統的設備量和成本，加重系統進行數據處理的負擔，并對天線布局安裝提出了很高的要求［8］，而且對短基線干涉儀測量精度的要求也非常高。

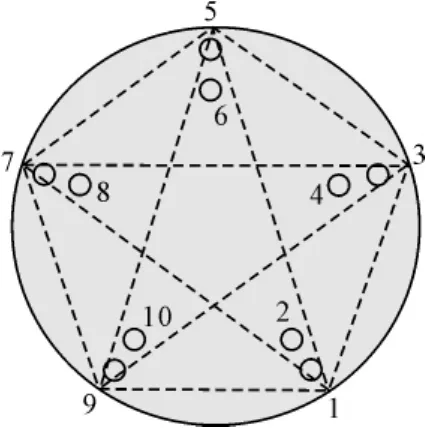
圖5 基于長短基線十陣元天線陣列設計圖

在均勻圓陣干涉儀測向系統設計中，已從理論上證明了5陣元以上的奇數個陣元以及8單元以上的偶數個陣元不存在測向模糊［9］。但是對于機載測向系統來說，由于機載平臺可供布設天線陣列的有效空間、允許的天線陣元尺寸和數量都十分有限，不能使用大基礎天線陣；另外飛機機身的金屬蒙皮結構會引起測向天線幅相特性的變化，這些都增加了機載測向天線布陣的難度和復雜性［10］。

從測向精度方面來考慮，十陣元比五陣元精度更高，但考慮到工程實際：體積重量的限制、空間陣元的布置、經濟成本以及計算量等方面的要求；同時為更好地發揮一維和二維相位干涉儀的各自優點，現提出基于長短基線的十陣元圓陣干涉儀布置方案。如圖5，干涉儀總共有十個陣元，由五條短基線，五條長基線組成天線陣列，大大減小天線布陣空間。利用五組短基線可以快速唯一地確定相位差粗值，進而利用多組長基線可以提高精度。通過理論分析計算，該十陣元干涉儀能較好地滿足測向精度要求，尤其是實際工程的要求；同時不存在相位模糊，計算速度也比均勻十陣元圓陣干涉儀要快。

5 結語

通過分析一維、二維相位干涉儀測向系統的原理及特點，從工程實際出發，提出了一種基于長短基線十陣元測向天線陣設計，它最大限度地利用了載體的有效空間，較好地滿足了天線陣元數量適中、天線陣基線長度盡量大、不同長度的基線盡量多等要求。理論分析表明，使用該測向天線陣，能較好地解決機載測向設備在實際環境中的高精度測向問題，在工程實踐上具有廣闊的運用前景。

［1］毛虎，楊建波，劉鵬.干涉儀測向技術現狀及發展研究［J］.電子信息對抗技術，2010，25（6）：1－6.

［2］肖秀麗.干涉儀測向原理［J］.中國無線電，2006：43－49.

［3］安效君.改進的干涉儀測向方法研究［J］.無線電工程，2009，39（3）：59－61.

［4］田德民.影響干涉儀測向接收機測向精度的因素分析［J］.艦船電子對抗，2010，33（2）：45－48.

［5］司偉建.一種新的解模糊方法研究［J］.制導與引信，2007，28（1）：44－47.

［6］司偉建，初萍.干涉儀測向解模糊方法［J］.應用科技，2007，34（9）：54－57.

［7］王琦.圓陣干涉儀測向研究［J］.航天電子對抗，2009，25（5）：33－35.

［8］李勇，趙國偉，李滔.一種機載單站相位干涉儀解模糊算法［J］.傳感技術學報，2006，19（6）：2600－2606.

［9］Ding Qi，XIAO Xianci.DOA Ambiguity vs.Array Configuration for Subspace－based DF Methods［C］.Beijing：Proceedings of the 1996CIE International Conference of Radar Proceedings，ICR’96，1996：488－492.

［10］楊忠.一種基于干涉儀體制的機載測向技術研究［J］.無線電工程，2010，40（12）.