基于最小二乘曲線擬合法的皮帶垂度與張力關系研究

梅 松，周月娥，李東波，童一飛，袁延強

（1.南京理工大學 機械工程學院，南京 210094；2.鐘山職業技術學院 機電與汽車工程系，南京 210049；3.南京三埃工控股份有限公司，南京 211106）

0 引言

影響皮帶秤稱重系統精度要素之一就是張力，利用張力補償可以提高稱重長期穩定性和精度。張力越準確，稱重就越精確。因此，準確測得張力值十分重要。另外，張力不穩定是由機械的不平衡與磨損和電機響應運轉等方面造成的[1]。本文通過檢測皮帶垂度并對垂度數據進行算法處理，從而對張力的不穩定因素進行補償，最終根據研究得到的垂度與張力數學模型來計算出張力。

本文先理論推導出張力隨流量變化的數學模型，其次，通過離散垂度測量來建立垂度與流量的數據表，利用最小二乘曲線擬合法對垂度與流量曲線擬合，實現對數據的綜合分析，為研究物料流量與皮帶垂度的關系提供科學的參考依據[2]。然后對擬合結果進行分析，最終得到垂度、皮帶傾角等參數的張力數學模型。

1 現場輸送帶載料模型分析

現場的輸送帶安裝示意圖如圖1所示，在具體研究中簡化為圖2所示模型。

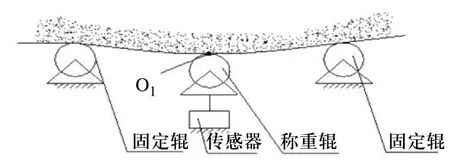
圖1 現場輸送帶載料

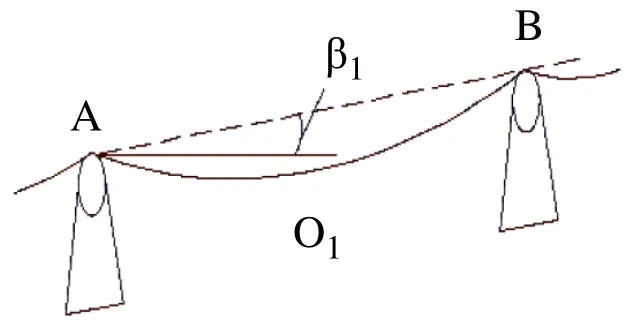
圖2 現場輸送帶載料簡化模型

其中，O1為托輥A,B之間輸送帶上的垂點，AB傾角為β1,其中虛線是輸送帶傳輸方向，實心直線為水平面，=L，根據實際測試，O1垂點對應的輸送帶撓度即垂度v＜3%L。現取一小段輸送帶O1D分析，建立xo1y坐標系，如圖3所示。

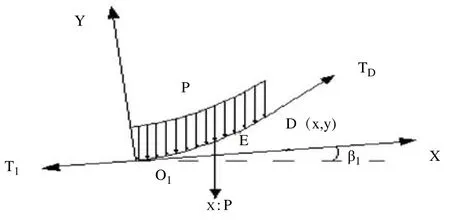
圖3 輸送帶O1D段受力分析圖

取O1為坐標原點，且以過O1點的切線為X軸，與X軸垂直作Y軸，其中，T1，TD分別為O1和D點處的張力，P為均布載荷；D點坐標為（x,y)，載荷重心坐標E(xe,ye),因輸送帶撓度較小,曲線O1D近似等于x。因此，O1D上負荷可視為平衡條件可得：

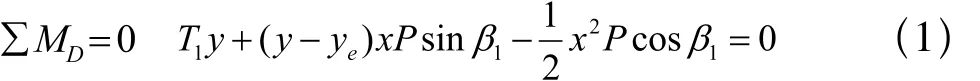
式中，MD為關于D點的力矩，P為皮帶及物料的質量分布簡稱流量， β1地面與水平面間的夾角。經整理得：

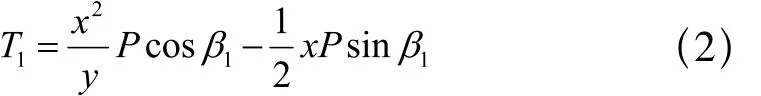
又已知O1為AB垂點，且為中間，因此可得x=L/2，代入上式得：

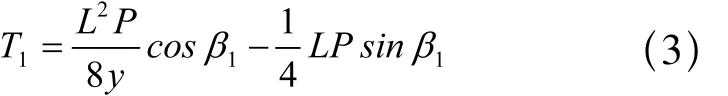
式中，L為兩托輥間的距離。其中，L與β1均為已知量。當P與y兩個變量檢測出來，對應O1點的張力也就隨之求出。

2 基于最小二乘法的垂度-流量曲線擬合

2.1 最小二乘法曲線擬合原理

假設流量fi與垂度xi，其中i=0,1,2,…,n。擬合關系為n次多項式，函數為其中a0，a1,…,an為下面方程組的解：

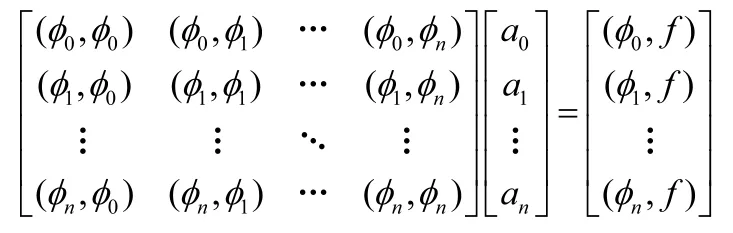
如果方程組中的系數矩陣為非奇異，則最優解唯一，這里 ， 是Rm+1上向量的加權內通過該方程使用Matlab軟件求解出系數a0，a1,…,an，就可以解得n次多項式[3]。

由于皮帶傳輸物料的重量不均勻，只有通過垂度值來反推出流量，從而進一步估算載物的重量，輔助稱重系統判定稱重單元計算結果的正確性與故障源。因此，研究物料流量固定，通過大量數據采樣得到垂度值，經均值數據處理，得到一組垂度與流量的數據，重復該方法獲取多組不同流量下檢測到的垂度值，來準確反映流量與垂度的關系。

2.2 流量與垂度實驗

實驗條件：1）標定初始值104mm；2）輸送帶預緊力為840kg；3）皮帶寬為1.2m；4）料斗下料給定值設為100t/h。

本實驗通過改變電機驅動輸送帶運轉的頻率來改變落在輸送帶的物料重量即流量，并檢測獲取相應的垂度，得到表1所示的9組流量范圍在14.62～46.3kg/m內的垂度與流量的關系數據。

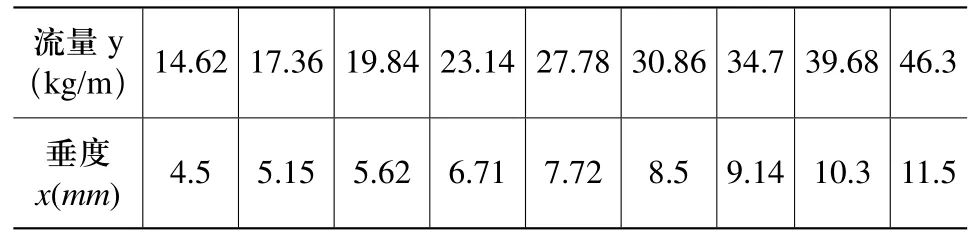
表1 垂度與流量數據關系

2.3 垂度-流量特性研究

根據表1數據采用Matlab對擬合模型y=a0x0+a1x+…+anxn進行多項式擬合，由最小二乘法確定多項式的系數a0，a1,…,an，通過擬合發現高于5次多項式曲線就會嚴重失真，因此只考慮5次以內擬合曲線，通過Matlab計算獲得各多項式曲線對應的殘差如表2所示。

表2 多項式擬合曲線殘差

由表2可以觀察到5次多項式擬合曲線殘差為0.80778，擬合效果最好，其擬合曲線如圖4所示。

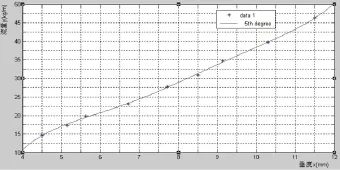
圖4 5次多項式擬合曲線

由圖可以觀察出數據與曲線擬合度非常好，因此選取5次多項式擬合曲線為最優擬合曲線，線方程[4]如下：

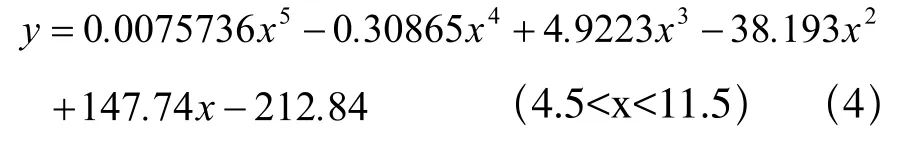
另外，根據皮帶本身性能和受力情況分析可以設想曲線y=f (x)是雙曲數據規律大致符合，可以通過變量代化為線性參數的數學模型其中(i=1,2,…,9)。其中ti,zi分別由原始數據xi, yi據變量代換公式計算出來，轉換后的數據表如表3所示。

表3 t,z關系數據

將以上計算值代入簡化方程組得如下方程組：

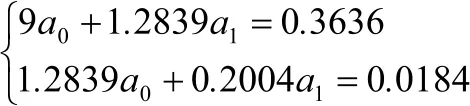
計算得a1=0.33822，a0=-0.0078494從而擬合曲線為

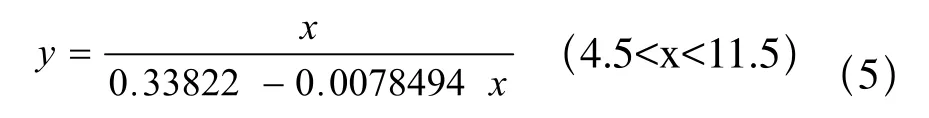
3 最小二乘法曲線擬合結果分析

3.1 擬合模型誤差比較

根據實測垂度數據，分別利用5次和雙曲型擬合曲線計算出輸送帶上的物料流量，進而計算出理論流量與計算流量之間的絕對誤差，誤差平方[5]。具體計算結果如表4所示。

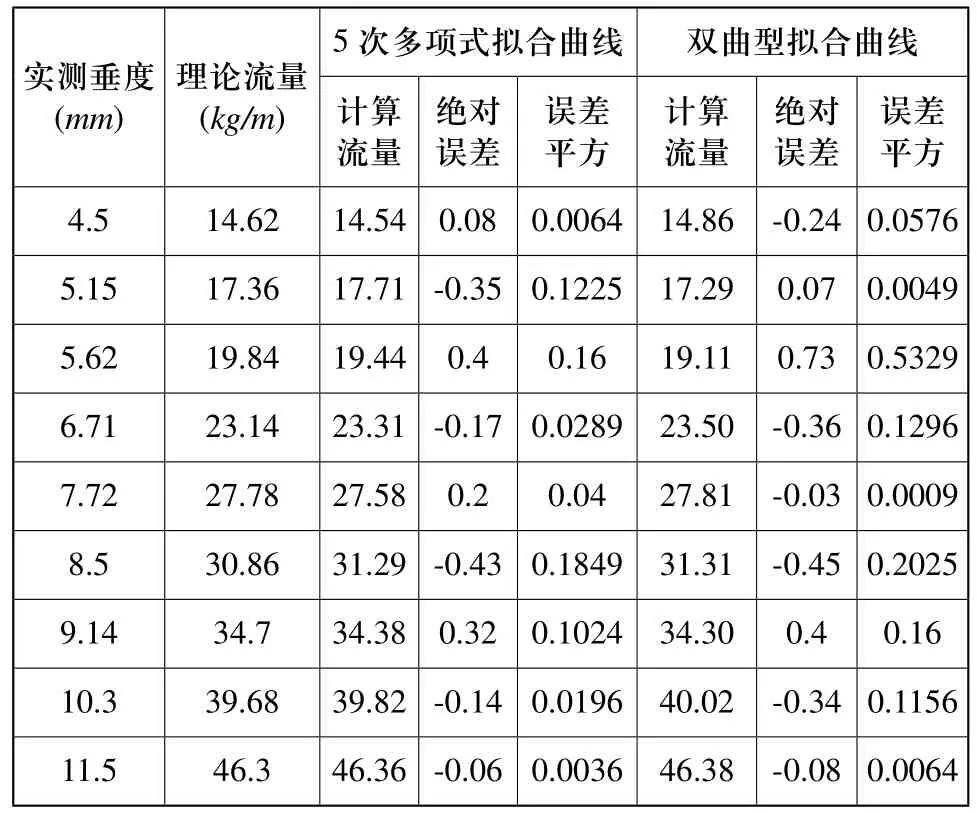
表4 5次多項式與雙曲型擬合曲線參與擬合數據分析

由表4算得5次與雙曲型擬合曲線誤差平方總和分別為0.6683,1.2104。5次多項式擬合曲線誤差平方更小，擬合效果更好。

由上表分析研究選擇5次多項式擬合曲線作為最優曲線擬合結果，其函數如下：

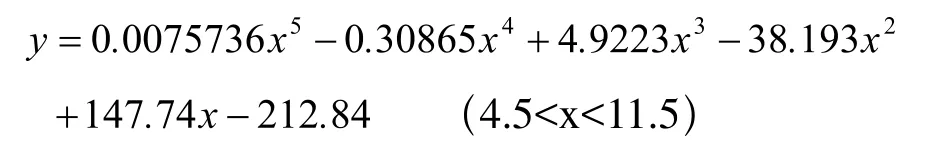
3.2 張力數學模型

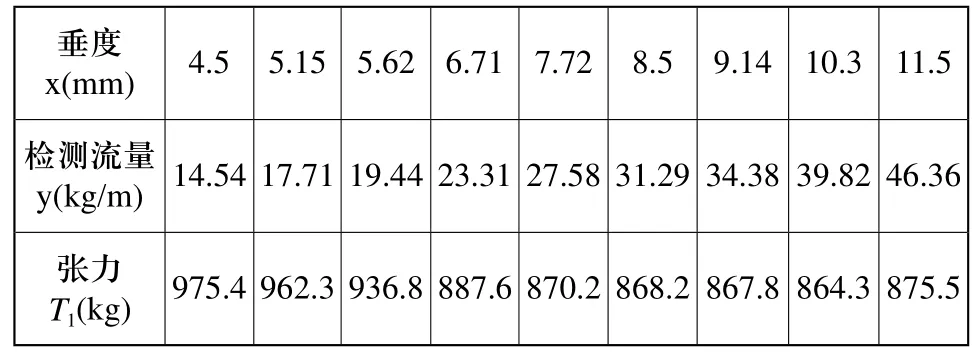
表5 垂度、流量與張力關系

從表5中可以觀察到垂度為4.5～10.3mm范圍內張力隨著垂度變大而減小，張力的極小值產生于垂度為10.3mm～11.5mm之間，張力自極小值之后會隨著垂度的增加而增加，由以上規律可判定張力與皮帶性能有很緊密的關系，可以在以后的實驗中作進一步研究。最終形成的張力與垂度的數學模型為：

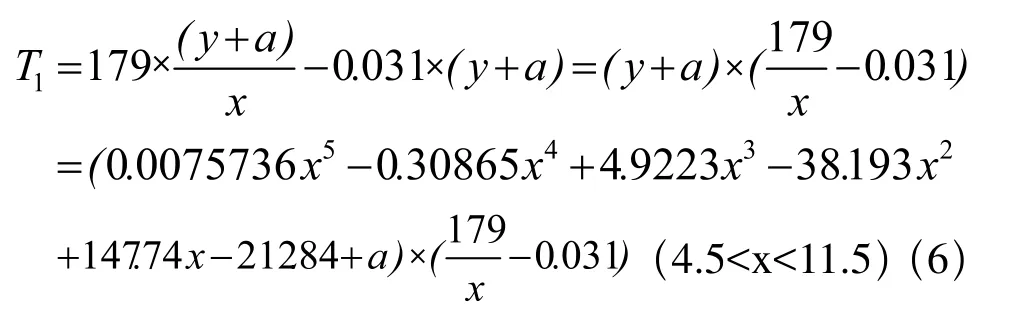
若將參數β1，L代入公式則可以轉化為

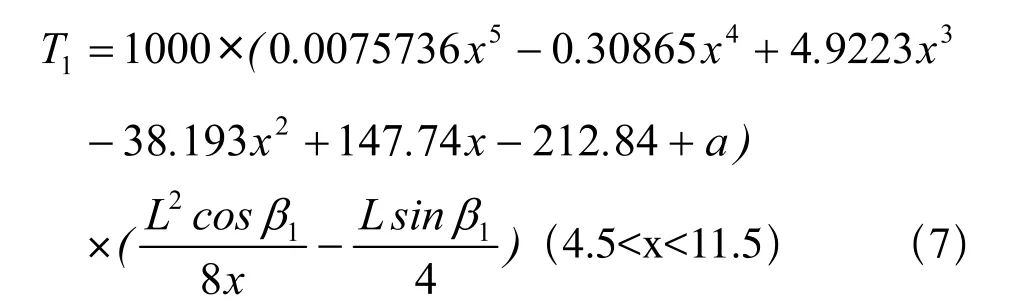
式中a為皮帶重量分布（kg/m）；x為測得的垂度值(mm); T1為張力（kg）；β1為皮帶與水平地面之間的夾角；L為兩托輥之間的距離(m)。

由公式（7）可以根據檢測到的垂度推算出張力。

4 結論

1）通過實驗獲取了流量與垂度關系的對應數據；利用最小二乘曲線擬合法研究垂度與流量的實驗數據，得到垂度與流量關系的擬合曲線；通過實驗驗證分析得出5次多項式擬合曲線為最優垂度與流量擬合曲線。2）根據最優垂度與流量擬合曲線及張力與流量數學關系建立了皮帶張力與垂度的數學模型。

[1] 李南, 劉秋楠. 有關高速傳帶設備張力控制的應用研究[J]. 制造業自動化, 2010. 2, 32(2): 132-133.

[2] 謝先偉. 最小二乘法在煤礦鉆機測試中的應用研究[J].制造業自動化, 2011. 5, 33(9): 59-60.

[3] 徐躍良. 數值分析. 成都: 西南交通大學出版社, 2005,08: 59-60.

[4] 呂喜明, 李明遠. 最小二乘曲線擬合的MATLAB實現[J].內蒙古民族大學學報(自然科學版), 2009. 3, 24(2): 126-127.

[5] 劉曉艷, 芮雪, 劉小勇. 基于正交多項式作最小二乘曲線擬合的水位流量率定系統設計與實現[J]. 新疆農業大學學報, 2009, 32(3): 89-90.