螺旋錐齒輪實體造型及有限元分析

劉漢超，汪中厚，莫 逗

(上海理工大學 機械工程學院，上海 200093)

0 引言

螺旋錐齒輪廣泛應用于航空、汽車、機床等領域，是重要傳動零件。所以加工的齒輪質量可靠是很關鍵的。為了順利加工出所需精度的齒輪,就需要在切齒前將各加工參數調整到合理的范圍內,并且將加工出來的齒輪進行分析檢測驗證。但是如果這些工作全部由實際的加工與分析來完成那就耗時長、成本高[1]。如果采用計算機仿真的方法，可以高效、準確、低成本的來完成所設計齒輪的性能預測。為此，則需要包含機床調整參數的三維實體模型來進行分析研究。目前的螺旋錐齒輪的實體建模仿真主要有兩種方式：一種是根據螺旋錐齒輪的設計公式，結合嚙合原理，計算出齒面點，然后進行齒面重構[2]。這種是通過數學方法得到的模型結果，與加工過程無關，未能包含機床調整參數。另一種是基于螺旋錐齒輪的加工過程，仿真齒輪成型的這一過程，從而獲得具有真實齒面的齒形[3]。這種方法可以反映機床調整參數，但是目前基于這種方法獲得的模型結果不可以進行有限元分析研究。因此若要分析某個機床加工參數下齒輪的質量時就要采用另外的解決方法。

所以針對這一問題，本文的研究出的解決方法是：首先，以第二種實體建模方法為基礎對螺旋錐齒輪進行切齒仿真，模擬螺旋錐齒輪加工過程，使切齒結果可以反映機床調整參數，并且齒面精確；然后，從切齒模型提取截面齒廓點進行齒面重構，從而得到連續完整齒面；最后，將重構模型導入有限元分析軟件進行分析，獲得機床調整參數對齒根彎曲應力影響的曲線，從而為研究機床調整參數對齒輪性能的影響提供了一種解決方法。

1 螺旋錐齒輪仿真加工

螺旋錐齒輪的切齒原理如圖1所示：機床上的搖臺機構模擬一個假想的齒輪，安裝在搖臺上的刀盤切削面是假想齒輪的一個輪齒。當被加工齒輪與假想齒輪以一定的傳動比繞各自的軸線旋轉時，刀具就會在工件輪坯上切出一個齒槽。切齒成型的過程就像是一對螺旋錐齒輪的嚙合過程[4,5]。

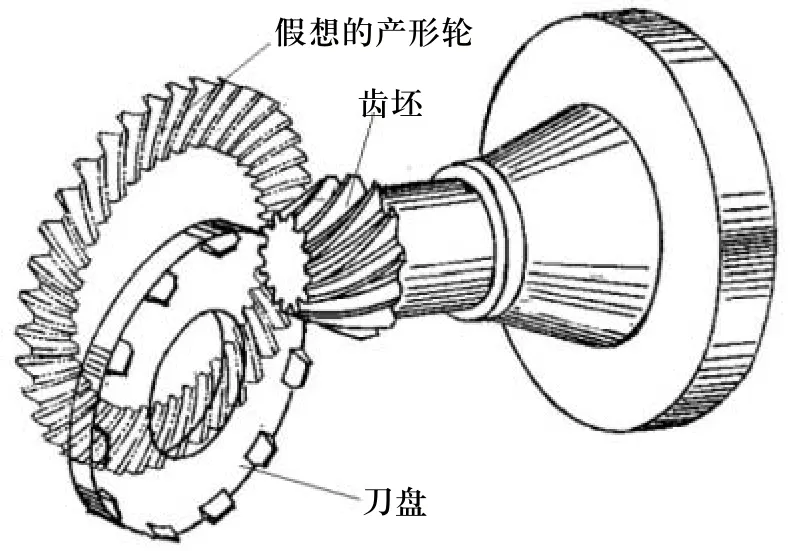
圖1 螺旋錐齒輪加工原理

基于這個原理，本文以一對準雙曲線齒輪為例，通過CATIA的二次開發編寫VBA編程來控制齒坯和刀具的相對運動完成切齒。具體實現過程為：首先是齒坯與刀具的建模。根據設計齒輪的尺寸參數，如表1所示，建立齒坯與刀具模型；然后根據切齒過程中的運動關系，編寫VBA程序。這個程序主要包括初始位置的調整以及切齒運動的控制，具體為切齒時的徑向刀位、角向刀位、床位、機床安裝角、軸向輪位、垂直輪位、滾比這7個參數的控制，如表2所示。最后程序控制齒坯與刀具的運動，并切出一個完整齒形，每完成一個切齒，齒坯轉動一個角度，一直到完成整個齒輪的切齒。圖2為大輪仿真結果。其中大輪是由單邊刀具一次切出凹凸面，小輪為雙邊刀分別切出齒輪的凹凸面。

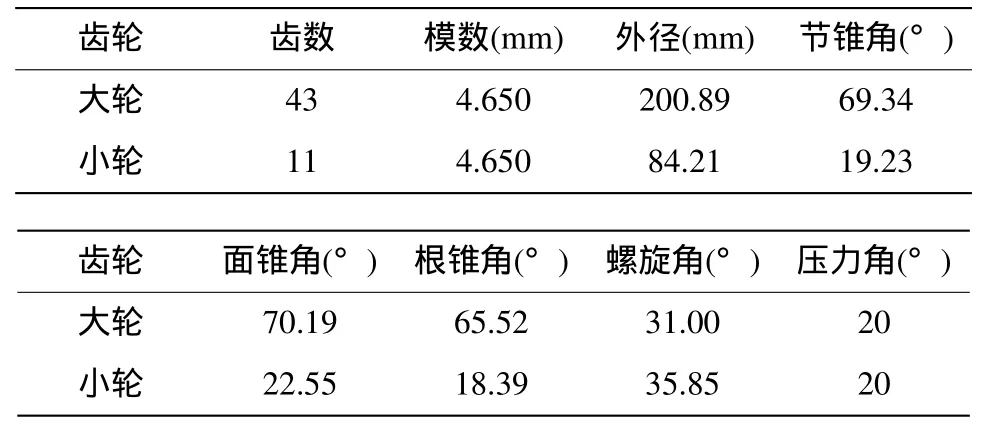
表1 準雙曲面齒輪基本參數

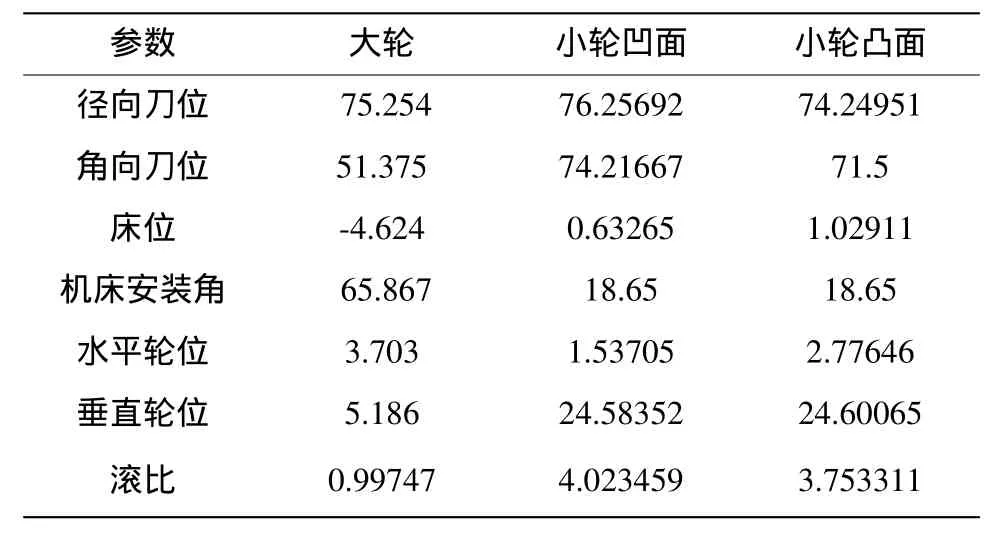
表2 齒輪加工機床調整參數

圖2 大輪切齒完成

通過改變VBA控制程序中的切齒調整參數，可以得到不同的切齒仿真結果。

2 切齒仿真結果的曲面重構

這種模擬加工過程的切齒方法獲得的三維實體模型有精度可靠的齒面[6]。但是由于在CATIA中仿真出的齒面為多步切齒產生的刀痕線構成，如圖3所示，在進行有限元分析時不能被識別成為一個完整的連續曲面，使切齒結果模型不能進行有限元分析，所以需要對齒面進行重構。由于PRO/E具有較為理想的建模模塊，并具備導出多種不同文件格式的內核，便于重構后的齒輪導入不同軟件中。所以齒面重構在PRO/E中完成。下面以大輪為例給出齒面重構過程。

圖3 大輪齒槽刀痕線

1) 在CATIA中，從一個完成多步切齒的齒槽提取齒槽面，如圖4(a)所示。

2) 建立等分的足夠多個旋轉截面使之與提取的齒槽面相交，如圖4(b)所示，此時可以得到旋轉截面與齒槽面上刀痕線的交點。提取這些交點轉存成IGS格式，IGS格式可以導入到多種有限元軟件中，如圖4(c)所示。

3)將刀痕線與截面的交點導入到PRO/E中，逐個選取這些交點建立樣條曲線，通過這些樣條曲線在PRO/E中重新建立齒槽曲面，形成一個連續、完整齒形，最后陣列得到整個大輪模型，如圖4(d)所示。

利用同樣的方法，可以對小輪進行重構。然后將重構之后的大輪與小輪在PRO/E里完成裝配。圖5為裝配好的一對齒輪模型。

3 齒輪彎曲應力分析

在研究機床調整參數對齒根彎曲應力的影響規律時，本文以徑向刀位這一參數對大輪齒根彎曲應力的影響為例進行研究說明。所以在大輪的VBA切齒控制程序中減小徑向刀位5mm,完成切齒后重構模型。這樣獲得的模型作為與標準模型（不改變任何機床調整參數所得切齒模型）的對比模型。將這兩對重構之后的齒輪副轉存為Parasoild.x_t格式后導入workbench中，進行有限元分析。

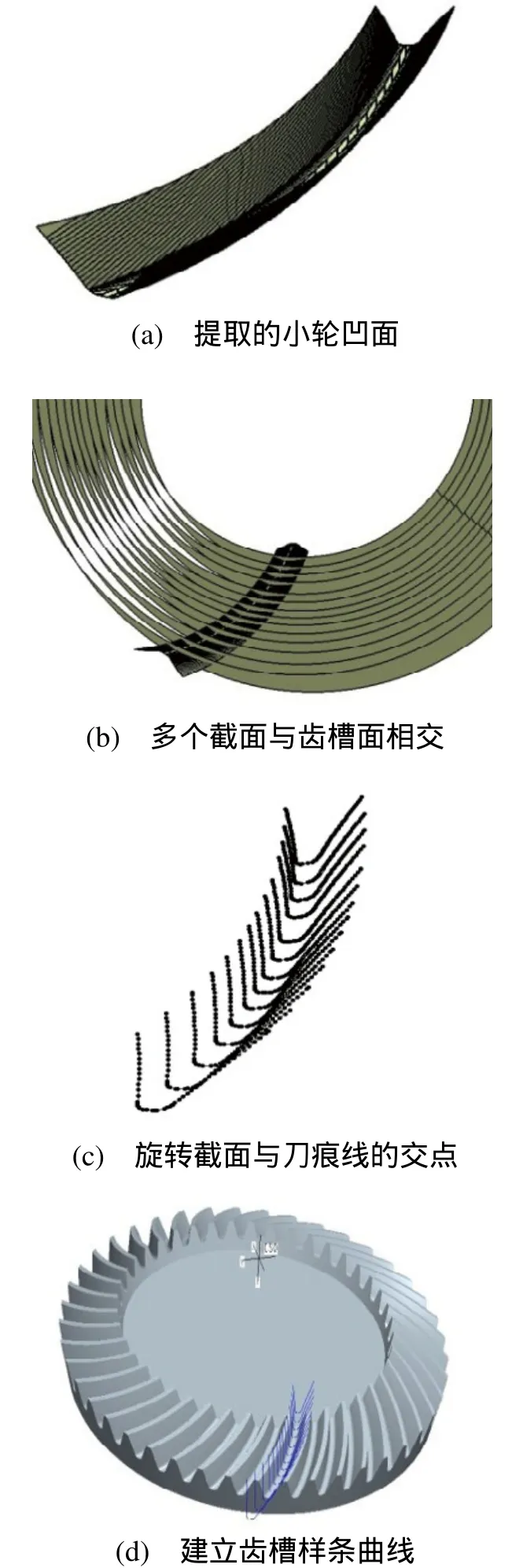
圖4 大輪齒面重構過程

3.1 分析前處理

1）選擇20CrMnTi為齒輪材料[7]。

2）接觸設置。選定大輪上的一個齒面作為觀察面，在轉動不同角度的情況下的對該面進行接觸設置。以轉動0°時為例，對大輪凸面和小輪的凹面的接觸設置。接觸類型為Frictional（摩擦），摩擦系數為0.06。

3）網格劃分。在赫茲公式驗證下[8]，經過多次接觸面網格劃分發現：當接觸面網格密度為0.45mm時有限元計算收斂。為節省計算時間其他網格選擇自動劃分。如圖6所示。

4）約束與確定載荷。用笛卡爾坐標系對大輪軸孔自由度全約束。小輪軸孔采用圓柱坐標約束，在轉動方向自由度放開其他方向約束。這里選用上汽通用別克-君威作為參考,最大功率達到108kw，最大轉速為6200r/min，為了使設計更具有參考性和通用性，這里取轉速6000 r/min，功率110kw。則由公式

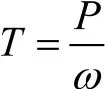
可得扭矩T=175N · M。其中，：齒輪軸角速度，rad/s，=2π n /60；n：齒輪軸的轉速，r/min，n=6000r/min；p： 齒輪軸功率，kw，取 P=110kw。

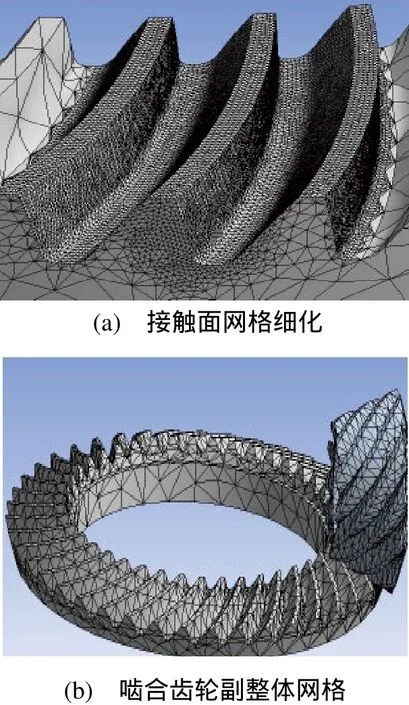
圖6 網格劃分

圖5 重構后齒輪副裝配圖

3.2 齒根彎曲應力

經過逐個角度的觀察嚙合的齒輪副模型，從與小輪嚙合前期的某一時刻起記為起點0°，一直到 1個嚙合周期結束附近，大輪轉過的角度為9°左右，以2°為單位對轉動角度在2°、4°、6°、8°等四處不同的瞬時嚙合狀態時的模型進行齒根彎曲應力分析。

標準模型與誤差模型嚙合狀態分別在2°、4°、6°、8°時的齒根彎曲應力曲線結果如圖7所示。從齒根彎曲應力應力曲線圖可以看出：徑向刀位減小5mm之后，齒根彎曲應力明顯增大，使得該參數下加工出齒輪的承載能力下降。

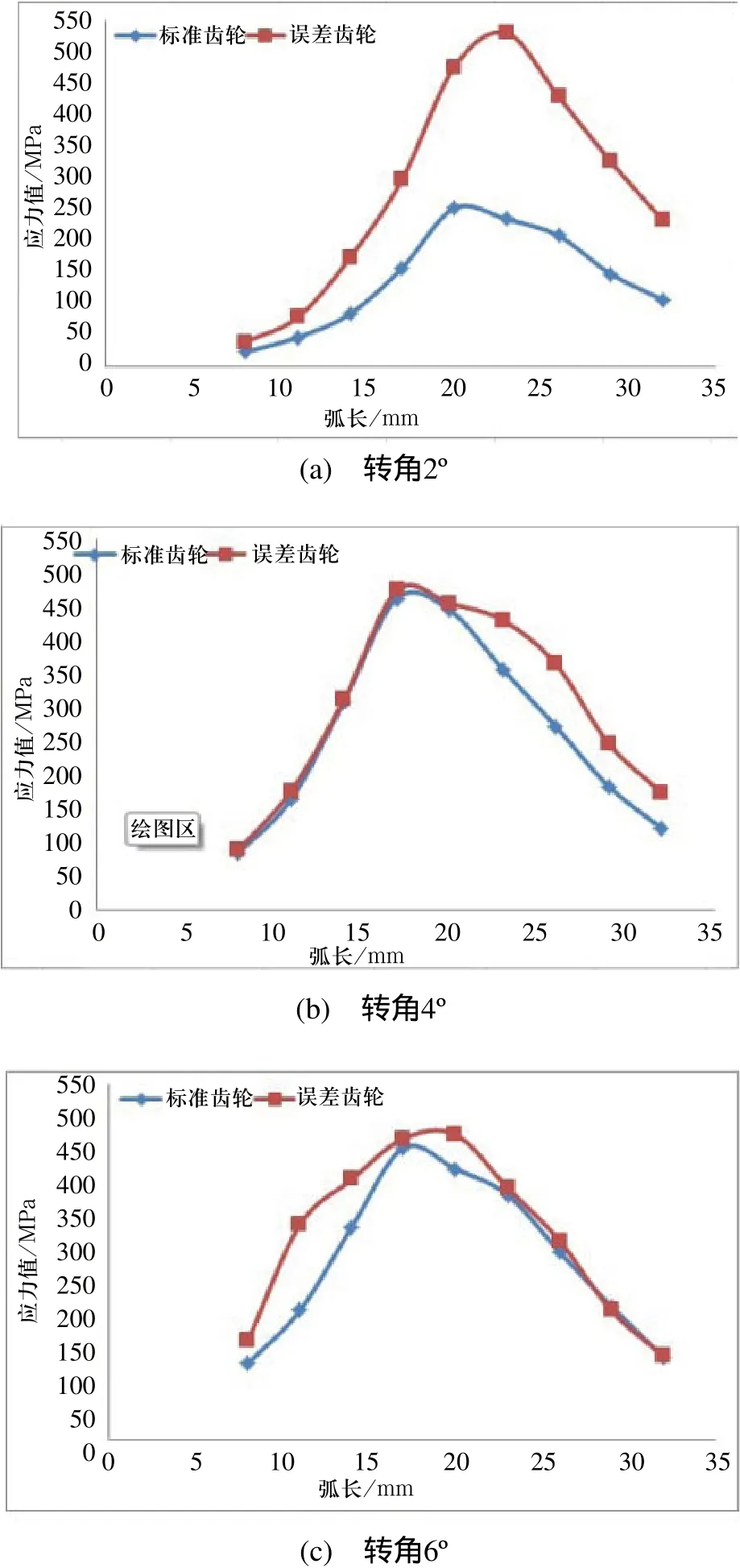
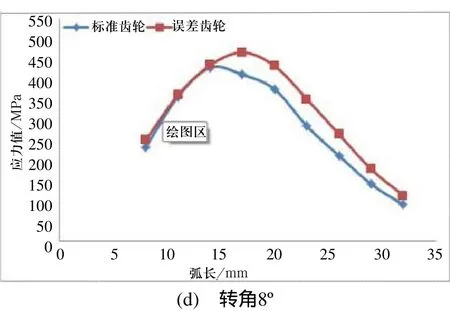
圖7 齒根彎曲應力曲線

4 結論

1)本文采用模擬螺旋錐齒輪加工過程切齒仿真的方法，快速獲得了包含機床加工參數的精準切齒結果。并能使齒面、過渡曲面及齒根曲面通過一次建模同時得到，有助于有限元分析的開展，可以為真實齒面的LTCA等研究創造基礎條件。

2)通過提取輪齒截面點的方法對切齒結果進行了齒面重構，獲得完整連續齒形面，使得重構模型可以進行有限元分析。

3)獲得了重構后的標準模型和誤差模型的齒根彎曲應力曲線結果。切齒仿真然后重構齒面這一方法可以為研究機床加工參數對齒輪的齒根彎曲應力的影響規律提供了一種有效途徑，為評價在一定加工參數下加工出的齒輪質量這一問題提供了一種解決方法。

[1] 謝華錕, 譯. 螺旋錐齒輪的開發:用計算機技術淘汰試切法[J]. 工具展望, 2006(4): 14-16.

[2] 李敬財, 王太勇, 等. 基于加工方法和嚙合理論的螺旋錐齒輪精確實體造型[J]. 吉林工大學報, 2008, 38(6): 1315-1319.

[3] 韓佳穎, 王太勇, 等. 準雙曲面齒輪切削仿真及齒面誤差分析[J]. 制造技術與機床, 2010,(1): 112-116.

[4] 北京齒輪廠. 螺旋錐齒輪[M]. 北京: 科學出版社, 1974.

[5] 曾韜. 螺旋錐齒輪設計與加工[M]. 哈爾濱: 哈爾濱工業大學出版社. 1989.

[6] 汪中厚, 莫逗. 螺旋錐齒輪切齒仿真和虛擬齒面誤差檢驗[J]. 現代制造工程, 2012, 1(1): 22-25.

[7] 傅蘭生. 中國齒輪工業年鑒[Z]. 北京: 機械工業出版社,1999.

[8] 張永棟, 謝小鵬, 等. 基于有限元法的齒輪接觸仿真分析[J]. 潤滑與密封, 2009, 1(1): 49-51.