球面艙壁的彈性穩定性分析
黃 旎,夏 飛,胡剛義,錢 群,肖 偉
(中國艦船研究設計中心,湖北 武漢 430064)
球面艙壁的彈性穩定性分析
黃 旎,夏 飛,胡剛義,錢 群,肖 偉
(中國艦船研究設計中心,湖北 武漢 430064)
基于靜力法求解結構臨界荷載的基本原理,導出旋轉殼在均勻外壓下彈性穩定性問題的一階控制微分方程組。借助齊次擴容技術和精細積分法,采用Riccati傳遞矩陣法對均勻外壓下球面艙壁的彈性穩定性問題進行數值求解。同時分析了各個參數(球殼半徑、球殼厚度、環殼半徑、環殼厚度和錐殼半錐角)對球面艙壁臨界壓力的影響。計算結果表明,各個參數中僅球殼半徑和球殼厚度對結構的臨界壓力和失穩波數起決定性作用。
球面艙壁;傳遞矩陣法;穩定性
0 引言
球殼由于其優越的承壓能力,被廣泛運用于壓力容器的端部結構。然而,球殼在外壓作用下容易喪失穩定性而發生屈曲。因此,穩定性是結構設計者必須考慮的因素之一。
球面艙壁在外壓下彈性失穩問題的研究,可以追溯到20世紀初。Zolly以扁殼理論為基礎,求出了球殼在外壓作用下的臨界壓力,即所熟知的球殼經典理論臨界壓力[1]。文獻[2]則從一般旋轉殼的理論出發,采用李茲法求解了軸對稱變形厚球殼的線性屈曲問題。Len Colgan等人同樣摒棄了扁殼理論的簡化假設,采用攝動法分析了軸對稱變形深球殼的線性穩定性問題[3]。然而,不管是從一般的殼體理論出發,還是以扁殼理論為基礎,研究的僅僅是單一的球殼結構。但是在耐壓容器的端部結構中,球殼與主耐壓體往往采用環殼過渡以降低接合的應力。因此,球面艙壁包括球殼扇形段和平滑連接的環殼嵌入件。
本文以與錐殼相連的球面艙壁為研究對象,從基于變形后的平衡微分方程出發,結合結構的幾何方程和物理方程,建立關于各個位移和內力分量為未知狀態向量的一階偏微分方程組。對于未知狀態向量,在周向利用三角函數展開分離后,結構的一階偏微分方程組轉化為一階常微分方程組,建立起結構各個殼段的傳遞矩陣,然后利用齊次擴容和細積分技術對微分方程組進行數值求解,計算結構的臨界壓力值。計算中研究了球殼半徑和厚度、環殼半徑和厚度、錐殼半錐角對結構臨界壓力的影響,可為球面艙壁的結構穩定性設計提供參考。
1 旋轉薄殼的基本方程
旋轉殼上任一點坐標可用曲率坐標(s,θ)表示,s為經向方向的弧長,θ為圓周方向角度,相應的主曲率半徑分別為R1和R2,則拉梅系數分別為A=1,B=r,如圖1所示。
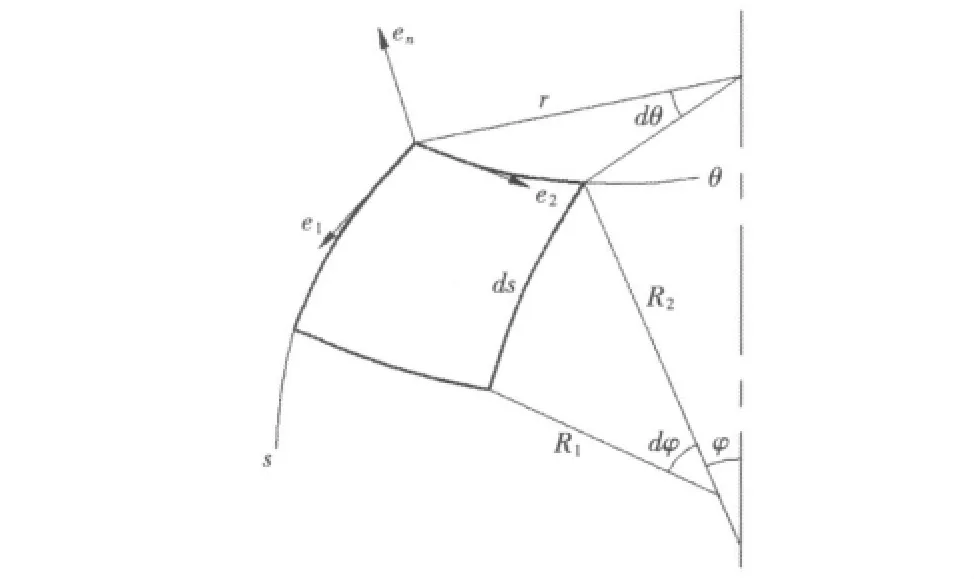
圖1 旋轉殼微元體Fig.1 The element revolutionary shell
設u,v,w分別為e1,e2和法向 en方向的位移分量。對于彈性薄殼,在曲率坐標系下,表征殼體中曲面的各個應變分量與位移分量之間的關系可表示為:
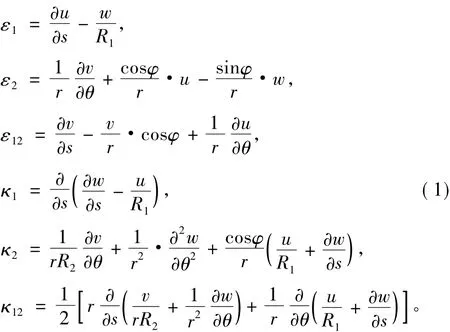
式中:ε1,ε2為中面沿e1,e2方向的薄膜應變分量;ε12為中面的面內剪應變;k1,k2和k12為彎曲應變分量。
在線彈性分析中,采用勒夫簡化的物理模型,即結構的各個內力與應變的關系式為:
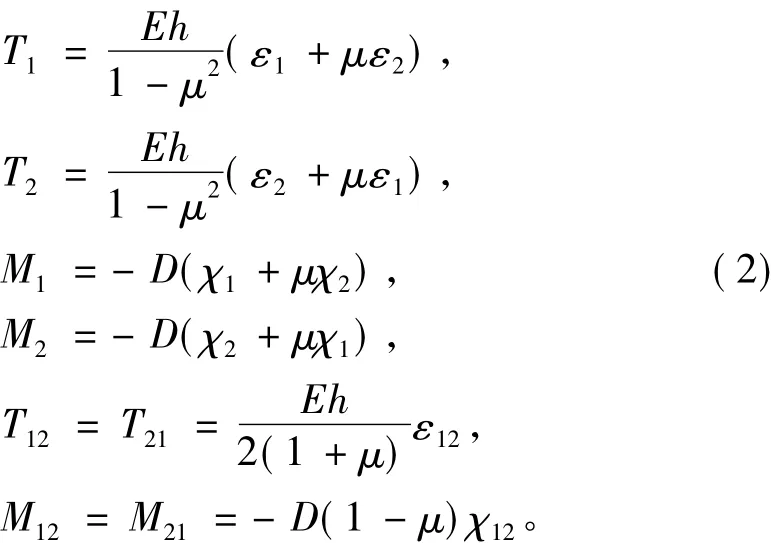
式中:T1,T2和T12為薄膜內力分量;M1,M2和M12為彎曲內力分量。
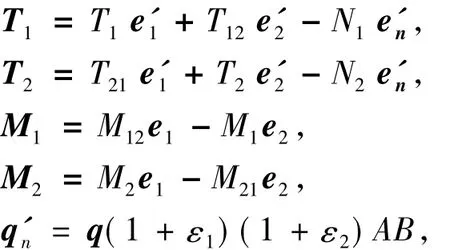
則微元體的平衡方程組為
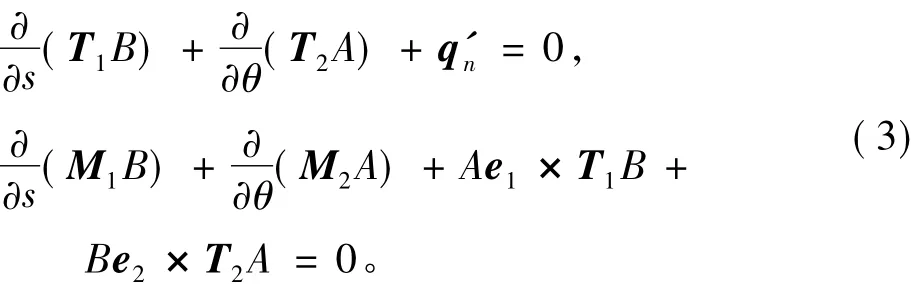
2 穩定性一階微分方程的建立和傳遞矩陣的推導
研究薄殼穩定性問題的手段主要有靜力法和能量法兩大類。筆者采用靜力法來研究球面艙壁的彈性穩定性問題。為計算結構的臨界壓力值,假設結構有2種不同的平衡狀態。假設在失穩之前,整個結構在薄膜應力狀態下保持穩定平衡,為狀態Ⅰ;在微小的擾動荷載下結構隨即失去薄膜應力狀態下的平衡,重新建立起微小彎扭變形狀態下的平衡,為狀態Ⅱ。為研究狀態Ⅱ的靜力平衡是否穩定,平衡微分方程需建立在新的變形狀態Ⅱ之下,即為上節的方程組(3)的各個展開式。由于狀態Ⅱ是非常接近狀態Ⅰ的平衡狀態,因此狀態Ⅱ下的各個內力TⅡ、內力矩MⅡ和位移UⅡ則可表示為狀態Ⅰ下的內力TⅠ、內力矩MⅠ和位移UⅠ與相應的增量T,M,U的和,即
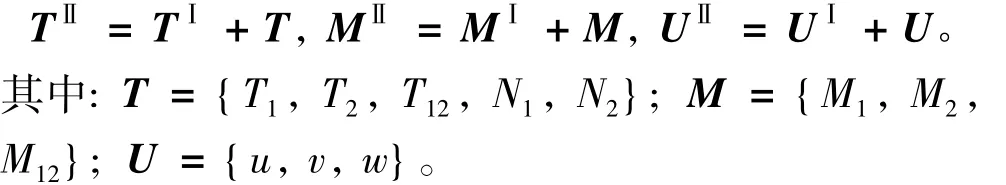
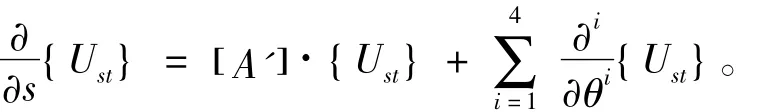
對向量{Ust}沿周向以三角函數分離變量[5]后,上式可改寫為
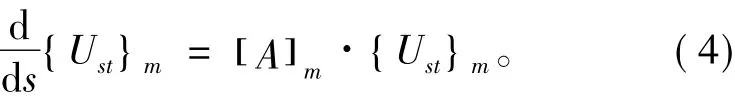
式中:{Ust}m={um,vm,wm,T1m,Fvm,Fwm,M1m},um,vm,wm,T1m,Fvm,Fwm,M1m為只與s有關的狀態函數。為求出臨界荷載值,假設給結構加一非常微小的撓動荷載。在該荷載作用下,分析狀態向量{Ust}m的某一狀態分量如法向位移wm。當該分量在壓力P為P0時,w突然增大或減小,則P0為結構的臨界荷載值。因此,式(4)將改寫為
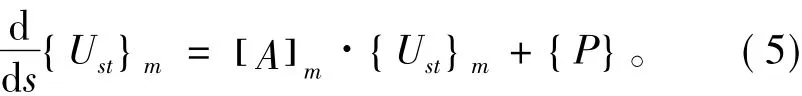
式(5)中的[A]m即為結構的傳遞矩陣,{P}為結構的微撓動荷載向量。球面艙壁是一種組合殼形式,將各個殼段的幾何特性代入[A]m中,可得到球殼、環殼和錐殼的傳遞矩陣的具體表達形式,同時在各個殼段的連接處用點傳遞矩陣傳遞,并用齊次擴容精細積分技術對式(5)進行求解[6]。
3 算例分析和參數研究
3.1 算例分析
左端固支的與錐殼相連的球面艙壁結構示意圖見圖2。圖中 R=1 000 mm,r=270 mm,L=781 mm,t=t1=7 mm,t2=10 mm,θ=82°。材料彈性模量E=2.0×105MPa,泊松比μ=0.3。
根據以上所述的傳遞矩陣法基本原理,采用Matlab編制與錐殼相連接的端部球面艙壁的穩定性計算程序。通過計算,結構的最小失穩臨界壓力Pcr=12.212 MPa,對應的環向失穩波數為14。最小臨界壓力下結構歸一化后的法向位移沿母線方向弧長的形狀如圖3所示。
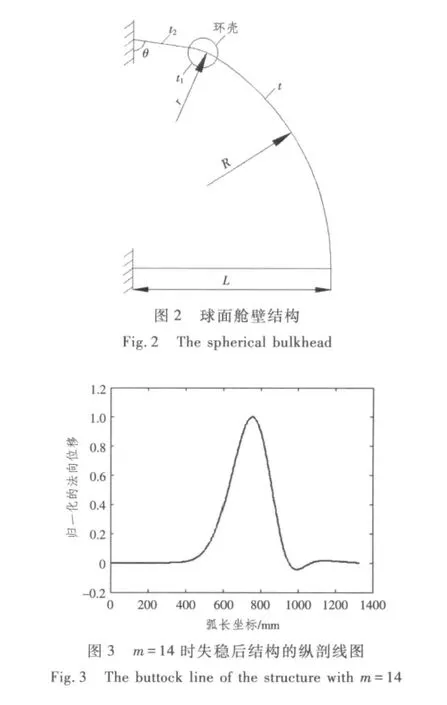
由圖中可以看出,結構在球殼部分上失穩,因此可采用球殼經典理論臨界壓力計算公式進行驗證。本算例中球殼部分的經典理論臨界壓力為11.86 MPa,二者誤差為2.9%。為了進一步驗證失穩波數的正確性,筆者采用Abaqus有限元軟件對結構的彈性穩定性進行分析,對比結果如表1所示。從表中可以看到,2種方法計算得出的環向失穩波數相同,失穩臨界壓力值十分接近,相對誤差不超過3%。
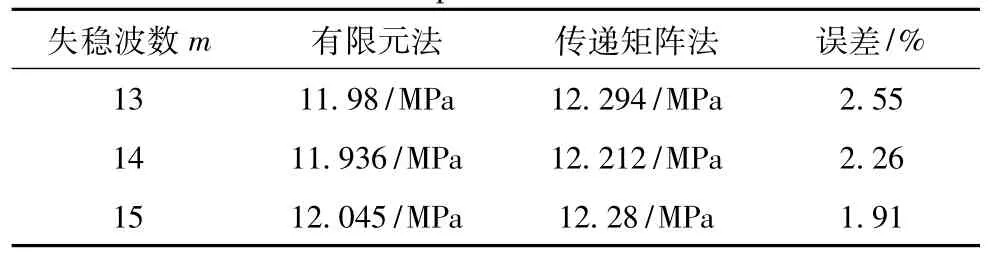
表1 失穩臨界壓力對比Tab.1 The comparison of the critical load
3.2 參數研究
在3.1節中基本結構的基礎上,保持其他結構參數不變,只改變某個參數的大小,計算該參數在各個數值下結構的臨界壓力。本文研究了球殼半徑、球殼厚度、環殼半徑、環殼厚度和錐殼半錐角對結構臨界壓力的影響,各個參數數值的改變如表2所示。

表2 各個參數數值Tab.2 The value of a series of parameters
計算結果表明:結構首先在球殼上失穩,這說明球殼是整個結構中的薄弱部分;隨著球殼半徑R的增大,結構的最小臨界壓力Pcr隨之減小,同時最小臨界壓力對應的失穩波數mcr也隨之變小,如圖4和表3所示;隨著球殼厚度t的增加,結構的最小臨界壓力隨之增大,對應的失穩波數mcr反而隨之變小,如圖5和表4所示;隨著環殼厚度t1、環殼半徑r和錐殼半錐角(π/2-θ)的增大,結構的最小臨界壓力有所增加,但增加的幅度很小,如圖6~圖8所示,且最小臨界壓力對應的失穩波數都不變,即mcr=14。
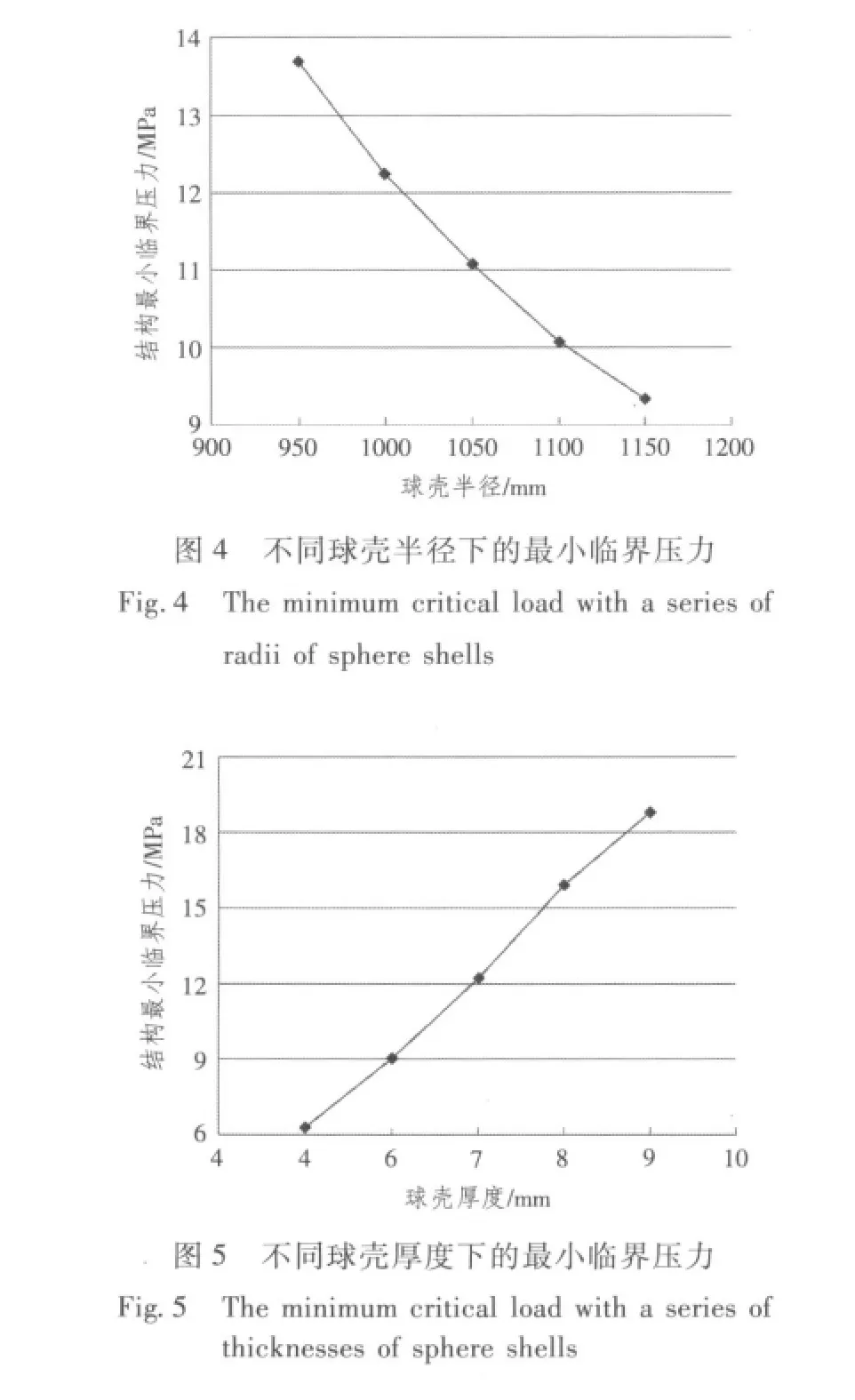

表3 不同球殼半徑下的最小臨界壓力Pcr和失穩波數mcrTab.3 The minimum critical load Pcrand the buckling wave number mcrwith a series of radii of sphere shells

表4 不同球殼厚度下的最小臨界壓力Pcr和失穩波數mcrTab.4 The minimum critical load Pcrand the buckling wave number mcrwith a series of thicknesses of spherel shells
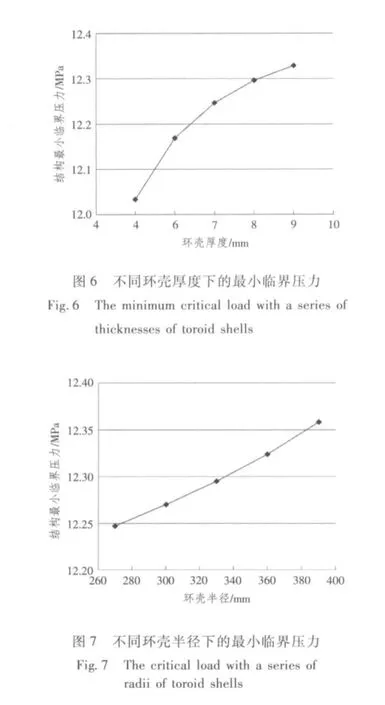
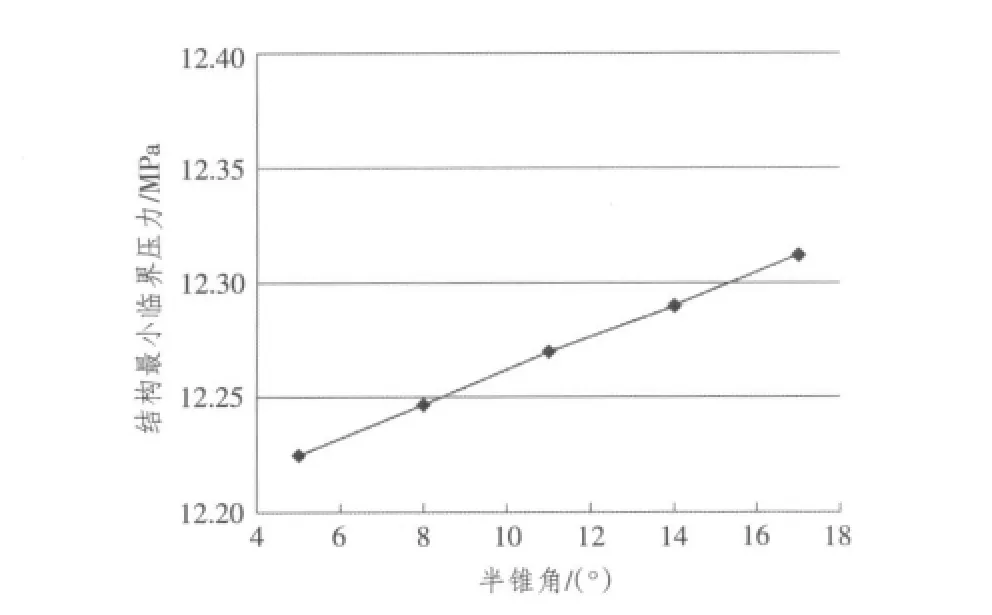
圖8 不同錐殼半錐角下的最小臨界壓力Fig.8 The minimum critical load with a series of slopes of the cone shell
4 結語
通過以上分析,對于與錐殼相連接的球面艙壁結構,可以得到以下結論:
1)采用傳遞矩陣法計算該結構的彈性穩定性問題是可行的,且具有很高的精度。
2)在各個參數中,球殼半徑及其厚度對結構的最小臨界壓力Pcr和失穩波數mcr起決定性作用。
3)當結構在球殼上失穩時,改變環殼厚度、環殼半徑和錐殼半錐角對結構的最小臨界壓力Pcr和失穩波數mcr的影響不大。
4)參數研究結果驗證了線性經典臨界壓力計算公式的準確性,對于整球殼、半球殼和不同高度的扁球殼均可采用經典公式確定其線性臨界壓力,而不必考慮邊界條件對其的影響。
[1]徐秉漢,朱邦俊,歐陽呂偉,裴俊厚.現代潛艇結構強度的理論與試驗[M].北京:國防工業出版社,2007.249-252.
[2]VO KK,WANG C M,CHA Y H,et al.Buckling analysis of moderately thick rotational shells under uniform pressure using the ritz method[J].Journal of Structural Engineering,2008,134(4):594 -601.
[3]COLGAN L,HOWLETT P,THREDGOLD J.A perturbation analysis to solve the linearequations forsymmetric deformation of a deep spherical shell[J].Mathematical and Computer Modelling,2009,49(5-6):918-935.
[4]楊耀乾.薄殼理論[M].北京:中國鐵道出版社,1981.10-12.
[5]白雪飛,任文敏,郭日修.組合加肋旋轉殼應力和穩定性分析的Riccati傳遞矩陣法[J].工程力學,2008,25(3):18-24.
BAI Xue-fei,REN Wen-min,GUO Ri-xiu.Stress and stability analysis of ring-stiffened joined revolutionary shell using riccati transfet matrix method[J].Engineering Mechanics,2008,25(3):18 -24.
[6]蘇海東,黃玉盈.分析旋轉薄殼的傳遞矩陣法[J].工程力學,2008,25(9):1-6.
SU Hai-dong,HUANG Yu-ying.A transfer-matrix method for analyzing revolutionary shells[J]. Engineering Mechanics,2008,25(9):1-6.
Elastic buckling analysis of spherical bulkheads
HUANG Ni,XIA Fei,HU Gang-yi,QIAN Qun,XIAO Wei
(China Ship Development and Design Center,Wuhan 430064,China)
Based on the theory of calculating the critical load by means of statics method,one-order ordinary differential equations for the elastic buckling of revolutionary shells is derived.By means of the extended homogeneous capacity and high precision integration method,the elastic buckling solution of spherical bulkheads is obtained by using Riccati transfer matrix method.And the influence of the parameter(the radius of the spherical shell,the thickness of the sphere shell,the radius of the toroid shell,the thickness of the toroid shell,and the gradient of the cone shell)is examined.The calculated result show that the radius and the thickness of the sphere shell play a vital role in buckling analysis.
spherical bulkheads;transfer matrix method;stability
U663.4
A
1672-7649(2012)07-0035-05
10.3404/j.issn.1672-7649.2012.07.007
2011-11-29;
2012-05-16
黃旎(1984-),女,博士研究生,研究方向為船舶結構設計與制造。

