輸入輸出反饋精確線性化他勵直流電動機轉速控制

魯 芳，史曉陽，盧斌文

（海軍航空工程學院 山東 煙臺 264001）

直流電動機由于具有良好的控制性能，主要應用于高性能調速系統。隨著科學技術的發展，人們對電動機的控制精度的要求越來越高。目前電動機調速系統仍在廣泛應用的傳統PID控制方法，具有控制器結構簡單、穩定性好、穩態精度高，可以在一定程度上改善系統的閉環的動態特性等優點。但是電機本身是一個復雜的非線性系統，這就使進一步提高以傳統線性化方法設計的轉速控制器動態性能變得十分困難。

隨著非線性控制理論的發展，使得在系統建模和系統控制中采用非線性方法成為可能。特別是以微分幾何為工具發展起來的反饋線性化方法受到了普遍的重視。它的核心思想是把一個非線性系統代數的轉化為一個 （全部或者部分）線性系統，以便可以應用線性系統的技巧[1-2]。精確線性化方法具有許多優點，如簡化模型的復雜度，在線性化過程中不忽略任何高階非線性項等。這種方法已經廣泛的應用到了開關變換器控制[3]，電動機控制[4-5]，水利系統[6]等領域。反饋線性化在控制領域的研究，大多采用狀態反饋線性化的方法實現非線性系統的完全線性化。但是狀態反饋線性化需要滿足嚴格的能控性條件和對合條件，而且存在控制器結構復雜，不利于工程實現等缺點。從實用角度來看，實現非線性系統完全精確線性化并不比部分精確線性化更為理想[6]。所以，研究基于輸入輸出線性化方法具有很高的理論價值和實用價值。

1 他勵直流電動機非線性模型及平衡點分析

電動機控制的目標是控制電動機轉速按照期望的指標運行。對于他勵直流電動機非線性系統，選取x=（ωiair）T作為狀態變量，選勵磁電壓ur為控制量，即u=ur，系統狀態方程[7]可寫為

設他勵直流電動機穩態轉速x1m=wm時，解方程組

由計算結果可知，對于給定的穩態轉速wm，有兩組穩態勵磁電壓、電樞電流、勵磁電流。可以看出b，組數據對應的穩態平衡點是物理上無法實現的，a組數據對應的平衡點是我們期望的電動機運行平衡點。所以當系統控制達到穩態轉速wm時，期望的穩態電樞電流x2ma，穩態勵磁電流x3ma。

2 非線性轉速控制器一

2.1 控制器設計

選擇輸出函數為 λ（x）=x1+Z1，此時系統的相對階 r=2，其中 Z2=wm（wm為電機期望運行角速度）為常數。 設 z1=λ（x），并對其進行求導，直到出現輸入量u，得

顯然，線性化后的系統是能控的線性系統，應用線性系統極點配置法設計閉環，即

則加入閉環控制的控制規律為

由于相對階r=2≠n，系統不能通過狀態反饋實現完全線性化，而只能實現輸入輸出線性化，即非線性系統的部分線性化。由非線性理論 可知，存在向量函數使得

則對應于輸出函數λ（x）=x1+Z1，非線性系統的內動態為Ψ˙=w（z，Ψ），式中 z=[z1，z2]。 求解偏微分方程（5），即

可得到該方程的一個解為Ψ=x2。

由（4）整理得：

上式（7）即為系統的內動態。

通過選擇系統的輸入使系統的輸出恒為零時，系統的內動態就是零動態。通過研究零動態的穩定性，可以得到內動態穩定性的相關結論。當z1=z2=0時，由（7）式可得系統的零動態為

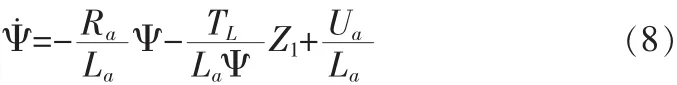
對零動態方程求導數，并將零動態方程平衡點帶入Ψ¨，判斷其正負，容易判斷零動態在平衡點附近漸進穩定，所以內動態在平衡點附近穩定。

2.2 仿真分析

據（5）式控制規律設計的控制器結構如圖1所示。根據不同的反饋控制方法設計的控制器的結構相似，只是反饋環節的設計不同。

圖1 電動機轉速閉環控制結構框圖Fig.1 Block diagram of Motor’s speed closed-loop control

其中的detect TL環節一方面是為了消除力矩變化引起的靜差，另一方面可以提高系統的抗力矩干擾能力。

文中選擇的電動機模型的負載額定轉矩為29.2 N·m，電樞電感為0.012 H，勵磁回路電阻為240 Ω，勵磁回路電感為0.12 H，電樞與勵磁回路互感為1.8 H，轉動慣量為1.0 kg·m2，電勢常數取經驗值k=15，電樞電壓為240 V，電樞電阻為0.6 Ω，額定轉速為100 rad/s。選擇極點配置參數k1=164，k2=23。圖2為電動機額定條件啟動狀態響應曲線。

圖2 額定條件啟動狀態響應曲線Fig.2 State response curve of start under rated conditions

從響應曲線中可以看出，當控制器將電機轉速穩定到期望轉速時（左側坐標），電機穩態電樞電流過大（左側坐標刻度），勵磁電流過小（右側坐標刻度），電機穩態是物理無法實現的電機模型平衡點，控制器設計無效。

3 非線性轉速控制器二

3.1 控制器設計

從控制規律（10）可知，基于狀態反饋線性化設計的控制律不是全局范圍成立的。當x∈U1={x∈R3|Lax2-Jx1=0}時，控制規律沒有定義好，即控制規律使狀態運行到這些奇點時，控制器不能使系統達到平衡點。所以控制器的反饋系數k1，k2不但要滿足線性系統穩定性判據的要求，而且必須能夠使得控制過程中的狀態軌跡與U1沒有交點，否則在交點位置控制器失效。

依據2.1中求零動態的步驟，可得對應于輸出函數λ（x）=x1+x2-Z2的Ψ可取為Ψ=x1，經計算系統的零動態方程為

對零動態方程求導數，帶入零動態平衡點，可知零動態在平衡點附近漸進穩定，所以內動態在平衡點附近穩定，控制器設計有效。

3.2 仿真分析

電機模型參數不變，奇點配置參數選為k1=542，k2=56。下圖3為控制器二控制的電動機額定條件下啟動狀態響應曲線。

圖3 額定條件啟動狀態響應曲線Fig.3 State response curve of start under rated conditions

從響應曲線中可以看出，電機啟動速度快，無超調，靜差小，且最終穩定在我們期望的電機模型平衡點，控制器設計有效。

為了考察系統的調速性能，在5秒的時調節控制控制規律，使電動機轉速從100 rad/s穩定到127 rad/s。圖4為電機調速狀態響應曲線。

圖4 調速狀態響應曲線Fig.4 State response curve of speed regulation

從圖中可以看出電機調速迅速，超調小，動態性能優良。

為了考察系統的抗干擾能力，首先控制電動機轉速達到額定穩態轉速100 rad/s，5秒時在電動機轉矩控制端加入大小為15 N.m的恒干擾力矩，電動機的轉速響應曲線如圖5所示。

圖5 力矩干擾轉速響應曲線Fig.5 State response curve under disturbance torque

從圖中可以看出，控制器具有很強的抗力矩干擾能力，在持續的大力矩干擾下能很好的穩定電動機轉速，并迅速恢復到額定轉速狀態。

4 結 論

文中以他勵直流電動機的數學模型為研究對象，應用輸入輸出反饋線性化理論設計了兩種電動機非線性轉速控制器，并從理論上證明了控制器內動態的穩定性。仿真過程中發現當非線性模型具有兩個平衡點，且兩個平衡點都穩定的情況下，通過選擇不同的輸出函數設計的輸入輸出反饋線性化控制器，可以使系統在零初始條件下穩定到不同的平衡點。仿真結果表明，本文設計的控制器具有很好的控制精度、動態性能和抗干擾能力。

[1]程代展.應用非線性控制[M].北京：機械工業出版社，2006.

[2]賀昱曜，閆茂德.非線性控制理論及應用[M].西安：西安電子科技大學出版社，2007.

[3]帥定新，謝運祥，王曉剛，等.Boost變換器非線性電流控制方法[J].中國電機工程學報，2009，29（15）：15-21.

SHUAI Ding-xin，XIE Yun-xiang，WANG Xiao-gang，et al.Nonlinear current control method for boost converter[J].Proceedings of the CSEE，2009，29（15）：15-21.

[4]孟昭軍，孫昌志，安躍軍，等.狀態反饋精確線性化永磁同步電動機轉速控制[J].中國電機工程學報，2007，11（1）：21-28.

MENG Zhao-jun，SUN Chang-zhi，AN Yue-jun，et al.Speed control of permanentmagnet synchronousmotor based on exact linearization via state variable feedback[J].Proceedings of the CSEE，2007，11（1）：21-28.

[5]曹建榮，虞烈，謝友柏.磁懸浮電動機的狀態反饋線性化控制[J].中國電動機工程學報，2001，21（9）：22-26.

CAO Jian-rong，YU Lie，XIE You-bai.Dynamic feedback linearization control for induction2type bearingless motor[J].Proceedings of the CSEE，2001，21（9）：22-26.

[6]李嘯驄，程時杰，韋化，等.輸出函數在單輸入單輸出非線性控制系統設計中的重要作用[J].中國電動機工程學報，2004，24（10）：50-55.

LI Xiao-cong，CHENG Shi-jie，WEI Hua，et al.Important effection of the output function in siso nonlinear control system design[J].Proceedings of the CSEE，2004，24（10）：50-55.

[7]李殿璞.非線性控制系統理論基礎[M].哈爾濱：哈爾濱工業大學出版社，2006：224-232.

[8]鮑海燕，楊建東，付亮.基于微分幾何的水電站過渡過程非線性控制[J].水利學報，2010，41（11）：1339-1345.

BAO Hai-yan，YANG Jian-dong，FU Liang.Nonlinear control of the transient process in hydropower station based on differentialgeometry theory [J].JournalofHydraulic Engieerig，2010，41（11）：1339-1345.