軟材料的低阻抗SHPB實驗技術與應用

張方舉，何 鵬，胡文軍，謝若澤

（中國工程物理研究院總體工程研究所，四川 綿陽 621900）

0 引 言

SHPB自發明以來，由于其結構簡單、數據處理簡便而越來越得到廣泛應用。全世界每年發表與SHPB相關的各類文章上百篇，文章主要集中于金屬材料的動態高率力學特性的研究，導桿材料多為高強度金屬材料，導桿的波阻抗與試件的波阻抗相匹配[1]。近10年來隨著科技的發展，隨著對安全與防護的日益重視，泡沫材料以及橡膠等低阻抗材料廣泛應用于如汽車的防撞、高速列車的緩沖以及各類包裝箱等包裝工程和沖擊防護工程。研究泡沫材料以及橡膠軟材料在各種沖擊載荷下的動態力學行為日益受到設計部門的重視[2－9]。由于這類材料的波阻抗與金屬導桿的嚴重不匹配，如泡沫材料的波阻抗不到鋼桿波阻抗的1/100，造成透射桿的輸出信號非常低，而反射波信號幅值與入射波信號幅值幾乎相同，造成信噪比低，數據處理帶來的誤差增大。

為了確保實驗能夠得到預期的結果，近年來國內外針對由于軟材料試件與壓桿之間波阻抗匹配的問題給出了一些解決辦法。通常解決這個問題的方法有兩種：一種是提高輸出桿上信號的信噪比，如采用靈敏度系數較高的半導體應變片代替電阻應變片[2]（前者的信號放大倍數約為后者的50倍）、在輸出桿中夾石英晶片[3]等；另一種則是改變桿材質與結構，選用與軟材料相適應的低波阻抗的輸出桿，如粘彈性桿[4，6-7]或空心桿[5]，粘彈性桿通常選用的聚合物材料有尼龍[8]和有機玻璃[9]等。前一種方法中，半導體應變片應變線性范圍較小，易受溫度的影響[10]，桿中夾石英晶片會額外增加界面；后一種方法中，空心桿雖然可以提高透射桿中的信號，但相應的端面應力較復雜，不滿足一維應力假定。采用低阻抗材料的聚碳酸酯（polycarbonate，PC）桿為一種比較好的方法，PC材料波阻抗與泡沫材料等低阻抗材料相匹配；但聚合物材料具有粘性效應，當波由應變片測點傳播到桿/試件接觸端時（或反過來，由接觸端傳到應變片測點時）會發生幅值衰減和波形彌散，因此需要對其進行修正。

本文以波傳播系數法為基礎分析了PC桿的粘彈性，得到了PC桿材料的衰減系數與彌散系數，建立了低阻抗SHPB處理方法。應用建立的低阻抗SHPB系數得到了泡沫和橡膠兩類典型低阻抗材料的動態高應變率力學性能。

1 低阻抗SHPB實驗系統

圖1為低阻抗SHPB裝置示意圖，其結構形式與常規金屬材料SHPB類似，僅是導桿材料有差異。低阻抗SHPB裝置中，導桿與彈丸材料均為聚碳酸酯，密度為 1.18×103kg/m3，波速為 1 420 m/s，導桿和彈丸直徑均為φ25 mm，子彈、入射桿及透射桿的長度分別為300，1 000和1 000 mm，應變片均位于壓桿的中部。通過調整空氣炮的氣壓可以改變子彈的速度，在入射桿上產生不同幅值的輸入脈沖，根據應變片在入射桿與透射桿上測得的反射和透射脈沖便可計算得到材料的動態應力-應變關系。圖2（a）為采用低阻抗SHPB裝置獲得的泡沫鋁銅合金典型實驗應變波形。為了與低阻抗SHPB相比較，選用波阻抗相對較小的鋁桿為導桿，得到的泡沫鋁銅合金材料應變波形圖如圖2（b）所示。兩者相比較可知，采用PC材料為導桿的低阻抗SHPB得到的應變波形中透射信號幅值大，信噪比高且入射脈沖的振蕩較小，波形曲線光滑，加載脈沖作用時間約400 μs，是采用鋁桿時的加載脈沖寬度的3倍左右。

圖1 低阻抗SHPB裝置示意

2 數據處理方法

在傳統金屬SHPB實驗中，當輸入桿中的輸入脈沖到達試樣界面時，一部分脈沖被反射，另一部分脈沖通過試樣透射進輸出桿。反射和透射脈沖的大小取決于試樣材料的性質。由于加載脈沖作用時間比試樣中波的傳播時間要長得多，在加載脈沖作用期間，試樣中發生多次內反射，使得試樣中應力很快趨于均勻化，因此可以忽略試樣內部波的傳播效應。由波導桿上的應變片記錄的應變脈沖信號，由三波公式（式（1）～式（3））或二波公式（式（5）～式（7））計算出試樣上的應變 εs、應變率ε˙s和應力 σs。

圖2 采用鋁桿和PC桿分別得到的泡沫鋁銅合金SHPB實驗應變波形圖

式中：ls——試樣長度；

As——試樣的橫截面積；

A0——波導桿的橫截面積；

C0——波導桿的彈性縱波速度；

E——波導桿的彈性模量；

εi，εr，εt——波導桿記錄到的入射脈沖、反射脈沖和透射脈沖。

根據SHPB試樣的均勻性假設，即試樣兩端應力相等可得：

將式（4）代入式（1）～式（3），可得

對于傳統金屬SHPB，波在導桿上傳播時，波的衰減和彌散可以忽略，因此在導桿中部記錄的應力波信號與導桿試件接觸端的應力波等價，可以由式（5）～式（7）得到試件的應力－應變曲線。而采用PC材料作導桿的低阻抗SHPB，波在導桿中傳播時將出現衰減和彌散現象，導桿中端記錄的應力波信號不能代表試件端面的應力波信號，而是需要進行波的衰減和彌散修正。圖3為入射波形在導桿中分別經過1000mm和2000mm的傳播行程后，也即第1、2次反射后的應變波形，其幅值發生衰減，并且各個波形之間存在一定的位相差。

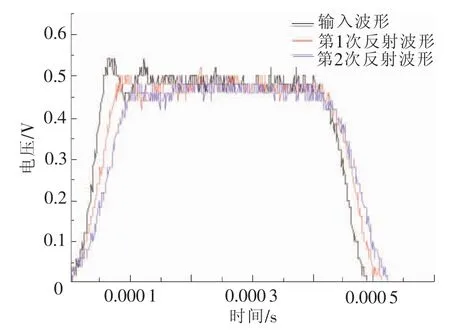
圖3 聚碳酸酯壓桿單桿實驗的入射與第1、2次反射應變波形

為了對應變信號進行修正，采用傳播系數法[7]對應力波在PC導桿傳播時的衰減和彌散進行修正，得到試件端面的信號，利用修正后的信號代入三波公式或二波公式計算試件的應力、應變和應變率。該方法對于所使用壓桿的截面形狀沒有限制，不必事先知道粘彈性桿的各種材料常數，因此十分方便，易于操作。

在一維假設前提下，經過傅里葉變換后可得頻域內的波動方程為

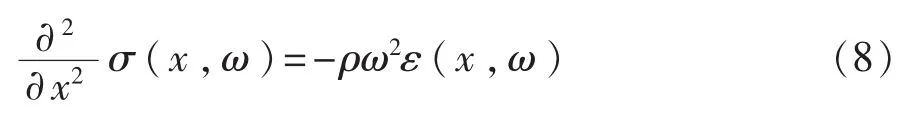
對于線性粘彈性材料，其一維頻域本構關系為

定義的傳播系數為

式（8）～式（10）中：ρ、ω 和E*——桿材料的密度、角頻率以及材料的復模量。

根據傳播系數的物理意義，可以通過式（11）將其與衰減系數（或阻尼系數）α（ω）以及相速度c（ω）聯系在一起，即：

其中 α（ω）為正的偶函數，且 α（0）=0，波數 k（ω）為奇函數，兩者皆為連續函數。對于線彈性桿，其衰減系數等于0，如果忽略幾何效應，則相速度與頻率無關，即應力波在傳播過程中不出現幾何彌散。

由圖3輸入波形，應用波傳播系數法，計算得到了應力波在PC導桿中的衰減系數α（ω）和相速度c（ω），見圖 4。由圖 4可知，隨著頻率的增加，其衰減系數和相速度增大。

圖4 PC壓桿的實驗傳播系數γ（ω）及入射波傳播波形預測與實驗記錄比較

根據傳播系數法對入射波傳播2 000 mm后的波形進行了預測，由于原始波形中含有高頻白噪聲信號，采用高頻濾波對原始波形進行了濾波，預測波形與實測波形見圖4（c）。由圖可見，預測波形與實驗實測波形之間除了一些細小的差異，總體上已能夠反映其基本特征，兩者間的差別主要是由于所計算的傳播距離較大造成的，當需要預測的傳播距離較小時，則得到的結果較好。

3 低阻抗SHPB的應用

3.1 試件

兩類材料：一類泡沫材料試件，其中聚氨酯泡沫初始表觀密度為193 kg/m3，試件尺寸為φ16 mm×8 mm；泡沫鋁銅合金初始表觀密度為390kg/m3，試件尺寸為φ20mm×10mm。另一類橡膠材料試件，硅橡膠184和硫化黑橡膠，試件尺寸分別為φ15 mm×8 mm 和 φ18mm×10mm。

3.2 泡沫材料實驗結果

實驗得到的聚氨酯泡沫的應力－應變曲線見圖5，泡沫鋁銅合金的應力－應變曲線見圖6。圖中準靜態實驗數據由INSTRON1196電子萬能材料試驗機得到，加載速率為2mm/min。

由圖5可知，聚氨酯泡沫的最大應變超過了60%，遠大于文獻[11]中采用金屬導桿得到的應變范圍，約為后者的6倍。其應力－應變曲線呈現出明顯的三階段變形特征，即線彈性階段、塑性壓潰（平臺）階段以及致密化階段。在2 000 s－1范圍內，應力－應變曲線對應變率敏感，隨著應變率的增加，其塑性流動應力增大，應變率為1700s－1時的流動應力約為準靜態時的1.6倍，與Sawas[12]報道的聚氨酯泡沫應變率敏感相一致。

圖5 聚氨酯泡沫的應力－應變曲線

圖6 泡沫鋁銅合金的應力-應變曲線

由圖6可知，泡沫鋁銅合金的動態應力-應變曲線與準靜態曲線類似，呈現出明顯的三階段變形特征，即線彈性階段、塑性壓潰（平臺）階段以及致密化階段。材料在所測應變率范圍內沒有表現出應變率敏感性。其應力平臺區的高度在不同的子彈速度下基本保持不變，且與準靜態曲線基本保持一致，但平臺區對應的應變范圍卻比準靜態的小得多，約為后者的一半。

3.3 橡膠材料實驗結果

圖7和圖8分別為實驗得到的硅橡膠184和硫化黑橡膠應力－應變曲線。由圖7可知硅橡膠184應力-應變關系在所測應變率范圍內呈線彈性，具有一定的應變率效應和較強的彈性恢復能力。

圖7 硅橡膠184的應力－應變曲線

圖8 硫化黑橡膠的應力-應變曲線

由圖8可知硫化黑橡膠在所測應變率范圍內，在應變20%以內應變率效應不明顯，應力-應變關系呈線彈性，與硅橡膠一樣具有較強的彈性恢復能力，從回收試件測量尺寸來看，在測試誤差范圍試件尺寸無明顯變化，顯示該橡膠材料具有超彈特性。

4 結束語

應用PC材料的SHPB系統的低阻抗，可實現波導桿與軟材料試件的阻抗匹配，長的加載脈寬，實現軟材料的高應變率大變形的動態壓縮力學性能測試；同時采用波傳播系數法對應力波在粘彈性PC桿中傳播時衰減和彌散進行修正，采用波傳播系數法預測應力波在粘彈性桿中波形與實驗測試結果基本一致。PC材料導桿與低阻抗材料的波阻抗相匹配，使透射波信號幅值顯著增加，提高了信噪比，建立的低阻抗SHPB實驗技術為研究泡沫、橡膠、塑料等材料動態力學性能提供了實驗技術支持。

[1]Field J E， Walley S M， Proud W G， et al.Siviour review of experimental techniques for high rate deformation and shock studies[J].International Journal of Impact Engineering，2004（30）：725-775.

[2]劉劍飛，王正道，胡適勝.低阻抗多孔介質材料的SHPB實驗技術[J].實驗力學，1998，13（2）：218-223.

[3]Chen W，Lu F，Zhou B.A quartz-crystal-embedded splithopkinson pressure bar for softmaterials[J].Experimental Mechanics，2000，40（1）：1-6.

[4]Wang L L，Labibes K，Azari Z，et al.A generalization of split hopkinson bar technique to using viscoelastic bars[J].International Journal of Impact Engineering，1994，15（5）：669-686.

[5]Chen W，Zhang B，Forrestal M J.A split hopkinson bar technique for low -impedance materials[J].Experimental Mechanics，1999，39（2）：81-85.

[6]王禮立，Pluvinage G，Labibes K.沖擊載荷下高聚物動態本構關系對粘彈性波傳播特性的影響[J].寧波大學學報，1995，8（3）：30-57.

[7]Bacon C.An experimental method for considering dispersion andattenuation in a viscoelastic Hopkinson bar[J].Experimental Mechanics，1998，38（4）：242-249.

[8]Limdholm U S，Yeakley L M.High strain-rates testing:tension and compression[J].Experimental Mechanics，1968（8）：1-9.

[9]Zhao H，Gary G，Klepaczko J R.On the use of a viscoelastic split hopkinson pressure bar[J].International Journal of Impact Engineering，1997，19（4）：319-330.

[10]尹福炎.電阻應變計技術六十年（一）：電阻應變計的由來，發展及展望[J].傳感器世界，1998（8）：27-32.

[11]盧子興，田常津，韓銘寶，等.聚氨酯泡沫塑料在應力波加載下的壓縮力學性能研究[J].爆炸與沖擊，1995，15（4）：382-388.

[12]Sawas O， Brar N S， Brockman R A.Dynamic characterization of compliant materials using an all-polymeric split hopkinson bar[J].Experimental Mechanics，1998，38（3）：204-210.