與非合作目標(biāo)交會(huì)的多約束有限時(shí)間最優(yōu)控制

鄧 泓，孫兆偉，仲惟超，陳長(zhǎng)春

（哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所，150001 哈爾濱）

與非合作目標(biāo)交會(huì)的多約束有限時(shí)間最優(yōu)控制

鄧 泓，孫兆偉，仲惟超，陳長(zhǎng)春

（哈爾濱工業(yè)大學(xué)衛(wèi)星技術(shù)研究所，150001 哈爾濱）

針對(duì)攔截衛(wèi)星的末端軌道攔截任務(wù)，研究了基于狀態(tài)反饋的軌道控制器設(shè)計(jì)方法.考慮系統(tǒng)參數(shù)不確定性，建立了相對(duì)運(yùn)動(dòng)模型.同時(shí)考慮系統(tǒng)有限時(shí)間二次型性能指標(biāo)、控制輸入限幅和極點(diǎn)配置，提出了多約束條件的控制器設(shè)計(jì)問(wèn)題并給出了控制器的設(shè)計(jì)方法.該方法采用線性不等式技術(shù)，根據(jù)Lyapunov穩(wěn)定定理推導(dǎo)出控制器存在的充分條件，并將控制器的設(shè)計(jì)轉(zhuǎn)化為一個(gè)凸優(yōu)化問(wèn)題進(jìn)行求解.仿真結(jié)果表明，設(shè)計(jì)的控制器能夠使系統(tǒng)穩(wěn)定，并且能在獲得最優(yōu)系統(tǒng)有限時(shí)間性能的同時(shí)滿足控制輸入限幅和極點(diǎn)區(qū)域限制.

軌道控制;不確定性;有限時(shí)間性能;控制輸入限幅;極點(diǎn)配置

攔截衛(wèi)星是指根據(jù)地面指令自動(dòng)接近并識(shí)別敵方衛(wèi)星，以實(shí)施攔截使其失效的人造地球衛(wèi)星［1］.攔截衛(wèi)星通過(guò)軌道控制實(shí)現(xiàn)對(duì)目標(biāo)衛(wèi)星的逼近.近年來(lái)，隨著推力器技術(shù)的發(fā)展，出現(xiàn)了推力可連續(xù)變化的噴氣推力器.由于推力連續(xù)可變，類似于衛(wèi)星姿態(tài)控制，許多控制理論可被用于軌道控制.文獻(xiàn)［2］針對(duì)交會(huì)對(duì)接中的軌道控制問(wèn)題，基于狀態(tài)反饋和自適應(yīng)控制理論設(shè)計(jì)了控制器，該控制器在系統(tǒng)存在有界干擾和測(cè)量噪聲時(shí)依然有效;文獻(xiàn)［3］提出了一種魯棒H∞狀態(tài)反饋軌道控制器設(shè)計(jì)方法，該方法通過(guò)優(yōu)化系統(tǒng)增益抑制系統(tǒng)外部擾動(dòng)，從而提高控制器的魯棒性;文獻(xiàn)［4］通過(guò)引入相平面，將Lyapunov穩(wěn)定理論用于軌道交會(huì)的控制器設(shè)計(jì)，并進(jìn)行穩(wěn)定性分析;文獻(xiàn)［5］將滑模控制理論用于軌道控制器的設(shè)計(jì)，與最優(yōu)控制相比，采用該方法設(shè)計(jì)的控制器具有更高的精度且便于工程實(shí)現(xiàn).可見(jiàn)，相對(duì)于傳統(tǒng)的沖量式軌道控制［6－8］，基于控制理論的變推力軌道控制方法具有更靈活多變的形式，并可以對(duì)系統(tǒng)穩(wěn)定性進(jìn)行分析，從而達(dá)到更高的控制精度.

攔截衛(wèi)星的攔截過(guò)程一般分為3個(gè)階段:地面引導(dǎo)段、自動(dòng)尋的階段和最后逼近段［1］.本文主要針對(duì)攔截衛(wèi)星的最后逼近段設(shè)計(jì)軌道控制器.為了快速完成攔截任務(wù)，以減少目標(biāo)衛(wèi)星發(fā)現(xiàn)并逃逸的時(shí)間，通常要求攔截衛(wèi)星的攔截時(shí)間(即變軌時(shí)間)越短越好，因此可考慮采用有限時(shí)間最優(yōu)控制.文獻(xiàn)［9－10］設(shè)計(jì)的控制器不僅使航天器完成了預(yù)期的軌道變化，同時(shí)還獲得了有限時(shí)間內(nèi)系統(tǒng)狀態(tài)性能指標(biāo)的最優(yōu)值.由于攔截衛(wèi)星的機(jī)動(dòng)性強(qiáng)，系統(tǒng)模型中的一些參數(shù)不可能實(shí)時(shí)精確計(jì)算.此外，由于目標(biāo)衛(wèi)星的非合作性和空間環(huán)境的復(fù)雜性，目標(biāo)衛(wèi)星的軌道角速度很難獲得精確值.因此，十分有必要研究不確定系統(tǒng)的控制器設(shè)計(jì)方法，文獻(xiàn)［11］和［12］分別對(duì)具有不確定參數(shù)的離散系統(tǒng)和連續(xù)系統(tǒng)設(shè)計(jì)了控制器.文獻(xiàn)［13－14］針對(duì)推力器的推力大小有限，研究了控制輸入限幅約束下的控制器設(shè)計(jì)方法.為了保證閉環(huán)系統(tǒng)具有一定的動(dòng)態(tài)特性，文獻(xiàn)［15］研究了極點(diǎn)區(qū)域約束下的控制器設(shè)計(jì)問(wèn)題.

然而，這些文獻(xiàn)在設(shè)計(jì)控制器時(shí)只考慮了其中一項(xiàng)或幾項(xiàng)約束條件，很少綜合考慮上述所有條件.本文提出了一種基于狀態(tài)反饋的控制器設(shè)計(jì)方法，該方法不僅在保證閉環(huán)系統(tǒng)漸近穩(wěn)定的同時(shí)優(yōu)化了系統(tǒng)的有限時(shí)間性能，還考慮了參數(shù)不確定性、控制輸入限幅和極點(diǎn)配置約束條件.

1 問(wèn)題描述

本文的攔截衛(wèi)星軌道運(yùn)動(dòng)是在相對(duì)參考坐標(biāo)系下描述的.該坐標(biāo)系的坐標(biāo)原點(diǎn)OI為目標(biāo)衛(wèi)星，XI軸沿目標(biāo)衛(wèi)星的矢徑方向，ZI軸與目標(biāo)衛(wèi)星軌道角動(dòng)量矢量方向一致，YI與XI、ZI軸構(gòu)成右手直角坐標(biāo)系.假設(shè)目標(biāo)衛(wèi)星的軌道近似圓形，且攔截衛(wèi)星相對(duì)目標(biāo)衛(wèi)星的距離遠(yuǎn)遠(yuǎn)小于目標(biāo)衛(wèi)星軌道半徑，則攔截衛(wèi)星相對(duì)目標(biāo)衛(wèi)星的軌道運(yùn)動(dòng)可由Hill方程描述:

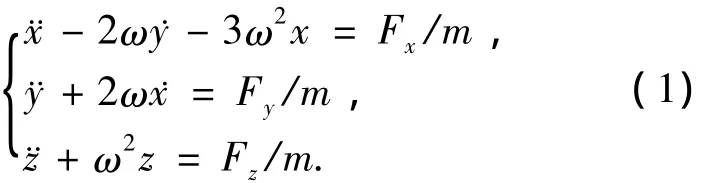
式中:x、y、z為相對(duì)參考系中攔截衛(wèi)星的位置分量;Fx、Fy、Fz為相對(duì)參考系下攔截衛(wèi)星的軌道控制力;ω為目標(biāo)衛(wèi)星的軌道角速度;m為攔截衛(wèi)星的質(zhì)量.

令狀態(tài)向量和軌道控制力向量分別為

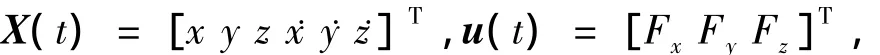
則攔截衛(wèi)星的相對(duì)軌道運(yùn)動(dòng)模型為

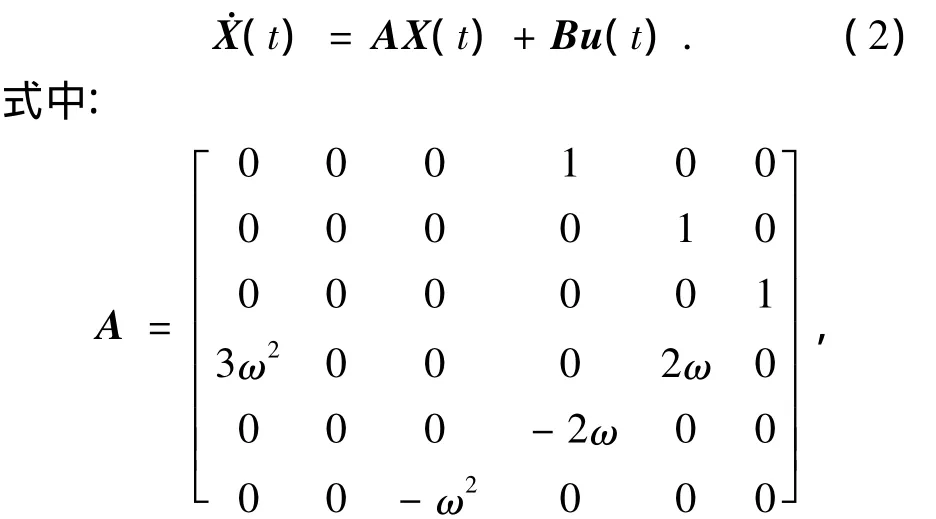
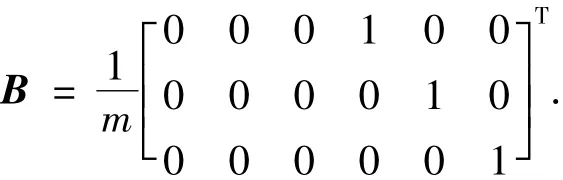
本文在設(shè)計(jì)控制器時(shí)，考慮了模型參數(shù)不確定性、系統(tǒng)的有限時(shí)間二次型性能指標(biāo)、控制輸入限幅和閉環(huán)系統(tǒng)極點(diǎn)配置多個(gè)約束條件.

1)不確定性.從式(2)可以看出，相對(duì)軌道模型的主要參數(shù)為目標(biāo)衛(wèi)星軌道角速度和攔截衛(wèi)星的質(zhì)量.然而，由于目標(biāo)衛(wèi)星為非合作目標(biāo)，且空間環(huán)境十分復(fù)雜，很難獲得精確的目標(biāo)衛(wèi)星軌道角速度.攔截衛(wèi)星在軌道機(jī)動(dòng)過(guò)程中，由燃料消耗引起的整星質(zhì)量變化也不可能實(shí)時(shí)精確計(jì)算.因此，可考慮目標(biāo)衛(wèi)星軌道角速度和攔截衛(wèi)星質(zhì)量的不確定性具有如下形式:

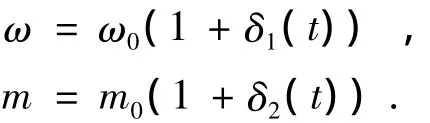
式中:ω0、m0分別為軌道角速度和衛(wèi)星質(zhì)量的理論值;δ1(t)、δ2(t)為不確定度且分別滿足|δ1(t)|≤1和 | δ2(t)|≤2;1、2均為不確定度幅值.

考慮上述不確定參數(shù)后，攔截衛(wèi)星的相對(duì)軌道運(yùn)動(dòng)模型可寫為

將不確定部分ΔA(t)和ΔB(t)均寫成范數(shù)有界不確定形式:

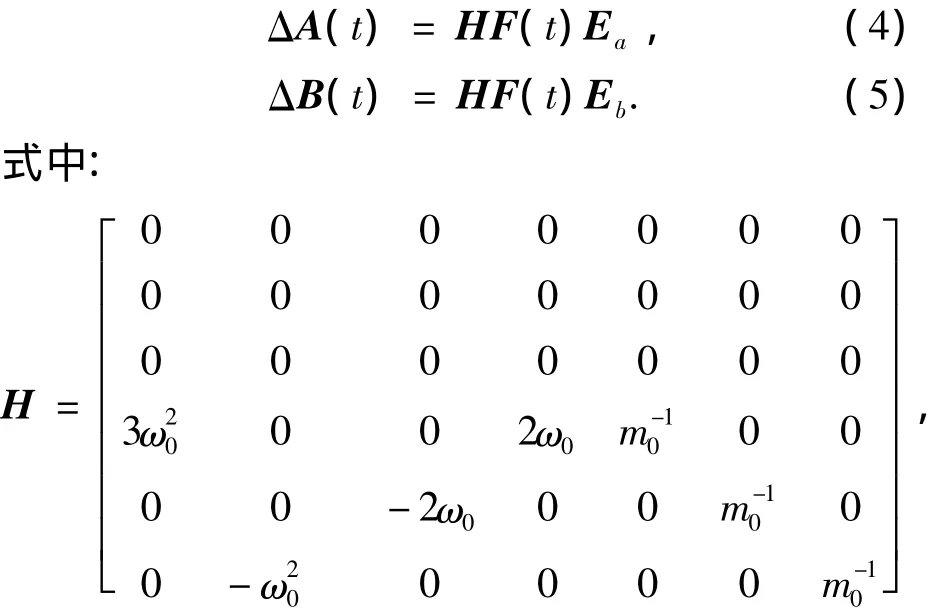
2)有限時(shí)間性能指標(biāo).由于攔截衛(wèi)星任務(wù)的特殊性，往往要求其能在有限時(shí)間內(nèi)達(dá)到預(yù)期軌道且燃料消耗小.因此，考慮如下系統(tǒng)狀態(tài)變量和控制變量的有限時(shí)間線性二次型性能指標(biāo)，通過(guò)設(shè)計(jì)控制增益陣K，使該性能達(dá)到最小:

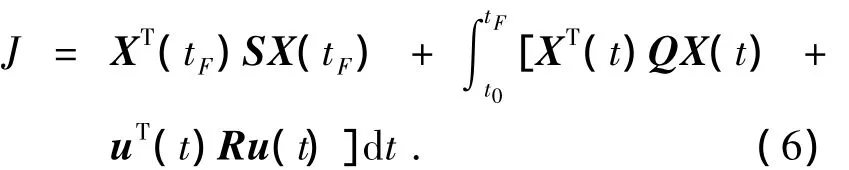
式中:S、Q和R均為已知的正定對(duì)稱矩陣;t0和tF分別為初始時(shí)刻和終端時(shí)刻.

3)控制輸入限幅.攔截衛(wèi)星進(jìn)行軌道機(jī)動(dòng)時(shí)一般采用噴氣推進(jìn)器.由于推進(jìn)器的推力有限，控制器的設(shè)計(jì)應(yīng)滿足

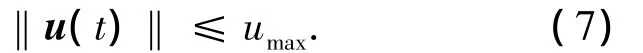
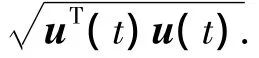
4)極點(diǎn)配置.由于模型的不確定性和各種擾動(dòng)，精確的極點(diǎn)配置很難實(shí)現(xiàn).若將閉環(huán)系統(tǒng)的極點(diǎn)配置在復(fù)平面上適當(dāng)?shù)膮^(qū)域中，可以保證系統(tǒng)具有一定的動(dòng)態(tài)特性.本文研究的是圓盤區(qū)域約束，即閉環(huán)系統(tǒng)的所有極點(diǎn)都在圓盤區(qū)域Θ(r，q)中，其中Θ(r，q)表示復(fù)平面上半徑為r，中心在(－q，0)的1個(gè)圓盤區(qū)域.

本文設(shè)計(jì)的控制器采用了狀態(tài)反饋控制，其結(jié)構(gòu)如下所示:

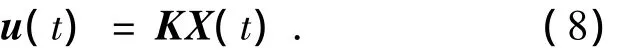
式中:K為狀態(tài)反饋控制增益陣.

故閉環(huán)系統(tǒng)可寫為

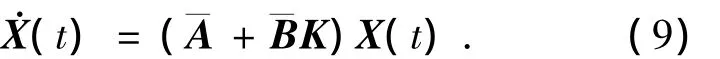
因此，本文的控制器設(shè)計(jì)問(wèn)題可描述為:設(shè)計(jì)控制增益陣K，使不確定系統(tǒng)(9)漸近穩(wěn)定且使系統(tǒng)有限時(shí)間二次型性能指標(biāo)J達(dá)到極小值;控制輸入滿足式(7);閉環(huán)系統(tǒng)極點(diǎn)都在圓盤區(qū)域Θ中.

2 控制器設(shè)計(jì)

為了證明后文提出的定理，在設(shè)計(jì)控制器之前先給出幾個(gè)引理.

引理1［3］設(shè)L、M和N為具有適當(dāng)維數(shù)的實(shí)數(shù)矩陣且滿足‖N‖≤1，則對(duì)于任意實(shí)數(shù)ε＞0，有

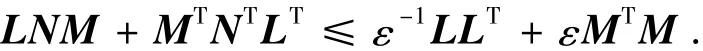
引理2［15］設(shè)Y、M和N為具有適當(dāng)維數(shù)的矩陣，其中Y是對(duì)稱陣，則對(duì)任意矩陣Γ滿足ΓTΓ≤I，有Y+MΓN+NTΓTMT＜0.當(dāng)且僅當(dāng)存在一個(gè)常數(shù) ε ＞0，使得Y+εMMT+ε－1NTN ＜ 0.

引理3［3］設(shè)M和N為具有適當(dāng)維數(shù)的矩陣，對(duì)于任意實(shí)數(shù)ε＞0，有

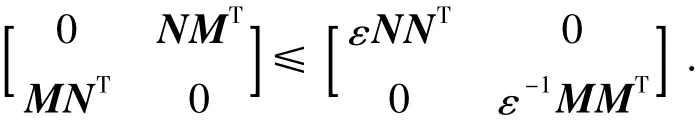
引理4(Schur補(bǔ)引理)［16］對(duì)給定的對(duì)稱矩陣

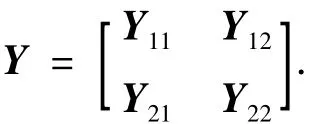
其中Y11是r×r維的，以下3個(gè)條件是等價(jià)的:

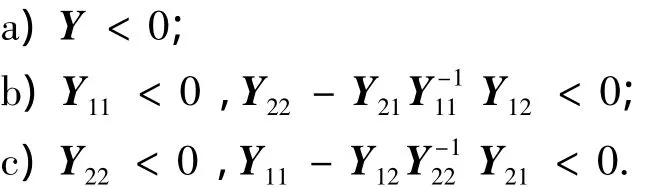
定理1 給定不確定系統(tǒng)(3)和狀態(tài)反饋控制律(8)，如果存在正定對(duì)稱矩陣P滿足

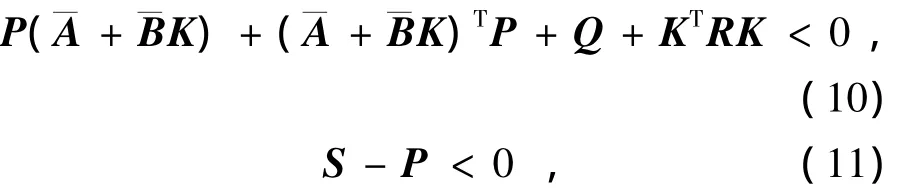
則閉環(huán)系統(tǒng)(9)漸近穩(wěn)定且性能指標(biāo)(6)有上界

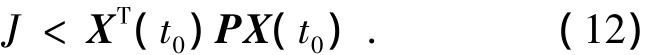
證明 因?yàn)镼和R均為正定陣，所以

由式(10)可得

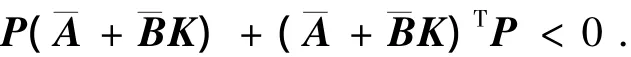
由Lyapunov穩(wěn)定定理可知，系統(tǒng)(9)穩(wěn)定，且Lyapunov函數(shù)為V(t)=XT(t)PX(t).

將式(8)帶入性能指標(biāo)(6)并考慮式(10)可得

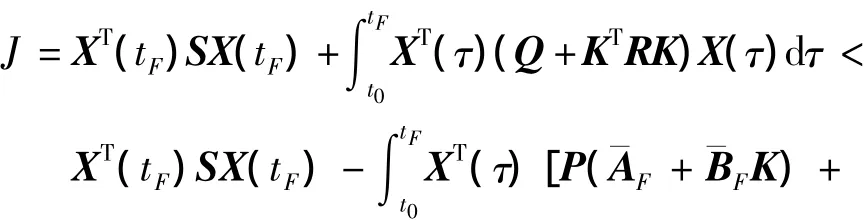
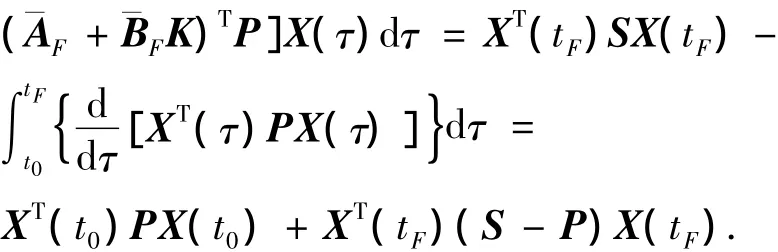
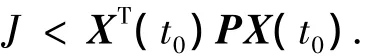
證畢.

定理2 給定不確定系統(tǒng)(3)和任意常數(shù)η ＞0，如果存在常數(shù) μ ＞0、λ ＞0、α ＞0和適當(dāng)維數(shù)矩陣Ω =ΩT＞0、Ψ滿足

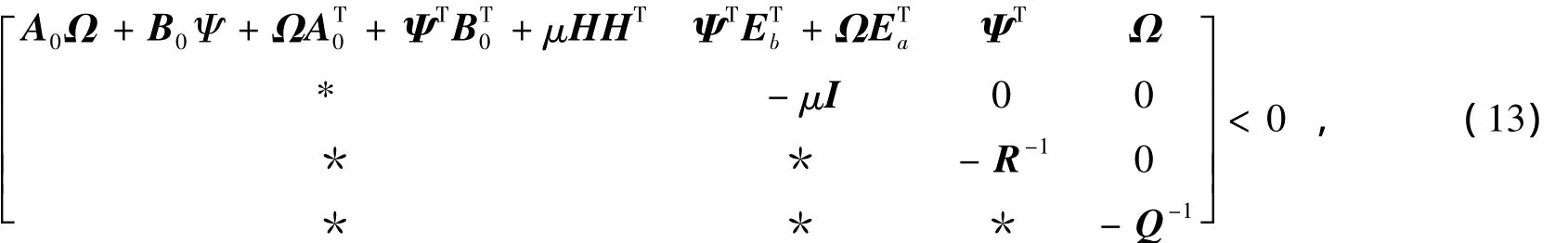
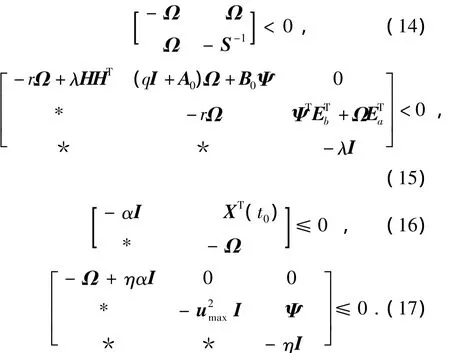
式中* 表示對(duì)稱陣.則存在狀態(tài)反饋控制律u(t)=KX(t)，使閉環(huán)系統(tǒng)(9)漸近穩(wěn)定并同時(shí)滿足控制輸入式(7)、閉環(huán)系統(tǒng)極點(diǎn)都在圓盤區(qū)域Θ中、系統(tǒng)有限時(shí)間二次型性能指標(biāo)有上界

且控制增益陣K可由下式計(jì)算:

證明 由定理1可知，如果不等式(10)和(11)都成立，則閉環(huán)系統(tǒng)(9)漸近穩(wěn)定且性能指標(biāo)(6)有上界.將不確定結(jié)構(gòu)(4)和(5)代入式(10)可得

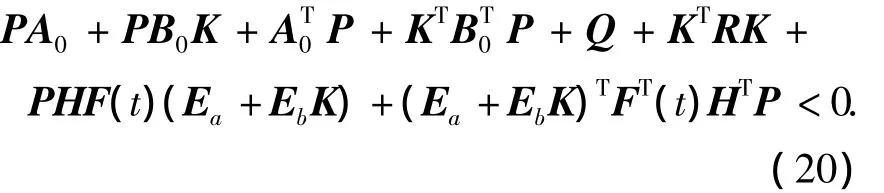
由引理2可得，存在常數(shù)μ＞0，使得當(dāng)下式成立時(shí)，式(20)成立.

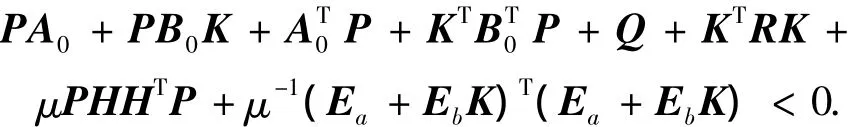
由Schur補(bǔ)引理可將上式寫成

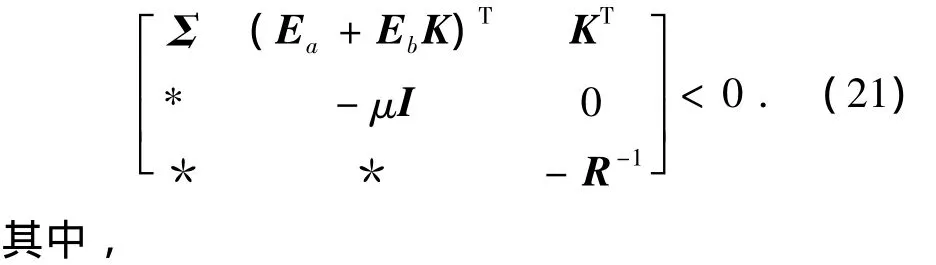
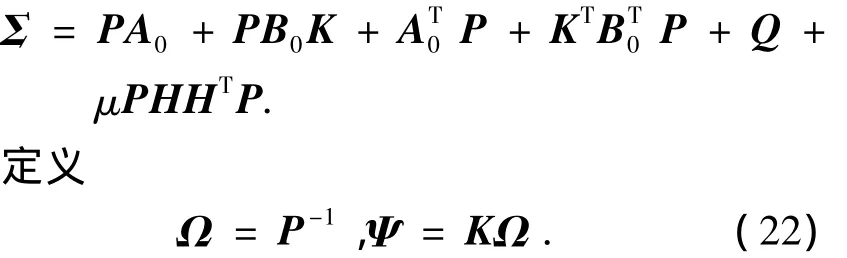
用 J1=diag(Ω，I，I)對(duì)式(21)做全等變換并再次利用Schur補(bǔ)引理，則可得到式(13).

用Ω對(duì)式(14)做全等變換得

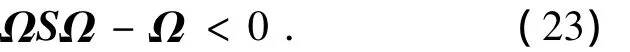
利用Schur補(bǔ)引理，則式(23)等價(jià)于式(14).

可見(jiàn)，當(dāng)式(13)和式(14)成立時(shí)，閉環(huán)系統(tǒng)(9)能漸近穩(wěn)定且性能指標(biāo)(6)有上界.

由文獻(xiàn)［15］可知，閉環(huán)系統(tǒng)(9)的極點(diǎn)都在圓盤區(qū)域Θ(r，q)中當(dāng)且僅當(dāng)

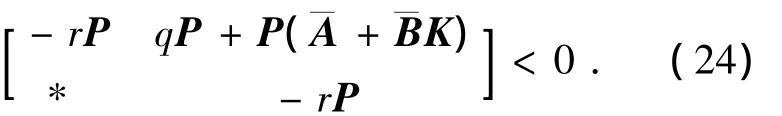
用J2=diag(Ω，Ω)對(duì)式(24)做全等變換并將不確定結(jié)構(gòu)代入.由引理2知，存在常數(shù)λ＞0，使得當(dāng)下式成立時(shí)，則式(24)成立.

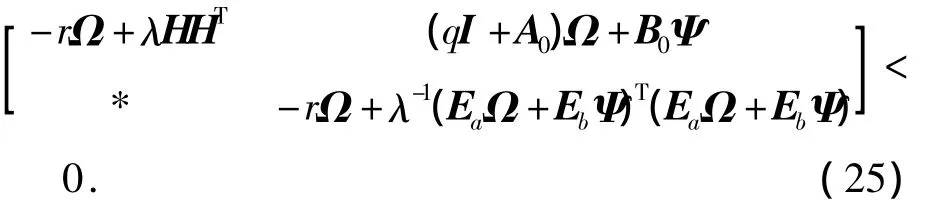
再由Schur補(bǔ)引理即可知，式(25)等價(jià)于式(15).即當(dāng)式(15)成立時(shí)，閉環(huán)系統(tǒng)(9)的極點(diǎn)都在圓盤區(qū)域Θ(r，q)中.

由文獻(xiàn)［17］可知，如果存在常數(shù)α＞0滿足

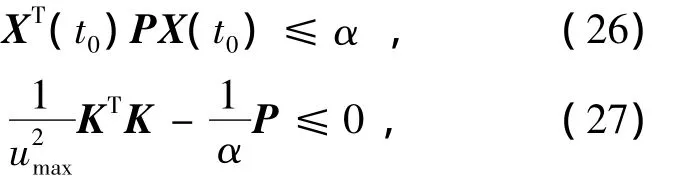
則控制輸入能滿足式(7).利用Schur補(bǔ)引理，可知式(26)和式(16)等價(jià).用Ω對(duì)式(27)做全等變換并根據(jù)Schur補(bǔ)引理可得

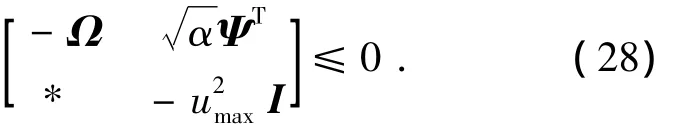
由引理3可知，對(duì)于任意常數(shù)η＞0，當(dāng)下式成立時(shí)，式(28)一定成立:

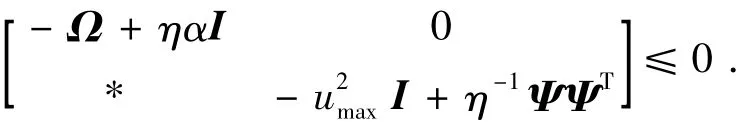
再由Schur補(bǔ)引理知，上式等價(jià)于式(17).可見(jiàn)，當(dāng)式(16)和式(17)成立時(shí)，控制輸入滿足式(7).

由式(12)和式(26)可知J＜α，即式(18)得證.由式(22)知，式(19)成立.證畢.

推論1 可以通過(guò)求解如下凸優(yōu)化問(wèn)題來(lái)設(shè)計(jì)狀態(tài)反饋控制器，并獲得系統(tǒng)有限時(shí)間二次型性能的最優(yōu)值:

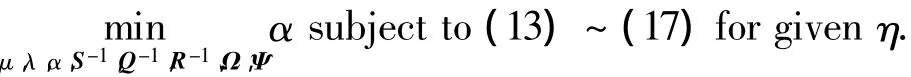
即對(duì)于給定的常數(shù)η＞0，尋找滿足不等式(13)～(17)的常數(shù)μ＞0、λ＞0、α＞0和適當(dāng)維數(shù)正定對(duì)稱矩陣 S－1、Q－1、R－1、Ω 和矩陣 Ψ，使得α值最小，則由式(19)計(jì)算可得控制增益陣K.

注: 在傳統(tǒng)的控制器設(shè)計(jì)中，通常先給定權(quán)矩陣S、Q、R.但在求解線性矩陣不等式時(shí)，給定權(quán)矩陣往往會(huì)增加解的保守性甚至無(wú)解［17］.因此，本文把權(quán)矩陣均看作變量矩陣進(jìn)行求解.

3 應(yīng)用實(shí)例與分析

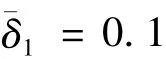
給定η =102，利用MATLAB中的LMI工具求解推論1，可J＜α=1.832 5.

則由式(19)計(jì)算可得控制增益陣為

根據(jù)上述設(shè)計(jì)的狀態(tài)反饋控制器，可仿真得到系統(tǒng)控制結(jié)果，如圖1～5所示.圖1和圖2分別為相對(duì)位置和相對(duì)速度變化圖.從圖中可知，相對(duì)位置和相對(duì)速度均快速收斂，在500 s內(nèi)分別收斂到10 m和0.1 m/s，800 s時(shí)分別為0.1 m和0.002 m/s.圖3為攔截軌道示意圖，可以看出，攔截衛(wèi)星以近似直線的路徑向目標(biāo)衛(wèi)星靠近，這樣可以減少被發(fā)現(xiàn)后目標(biāo)衛(wèi)星的反應(yīng)時(shí)間.圖4為三軸控制力曲線圖，可見(jiàn)推力均小于幅值500 N.圖5給出了開(kāi)環(huán)系統(tǒng)和閉環(huán)系統(tǒng)的極點(diǎn)位置.可見(jiàn)，開(kāi)環(huán)系統(tǒng)的極點(diǎn)均在零點(diǎn)附近，而通過(guò)控制器的設(shè)計(jì)，閉環(huán)系統(tǒng)的極點(diǎn)均在左半復(fù)平面，且處于圓盤區(qū)域Θ(1，1)中.由以上仿真結(jié)果可知，所設(shè)計(jì)的控制器是有效的，且滿足控制輸入限幅和極點(diǎn)區(qū)域限制.

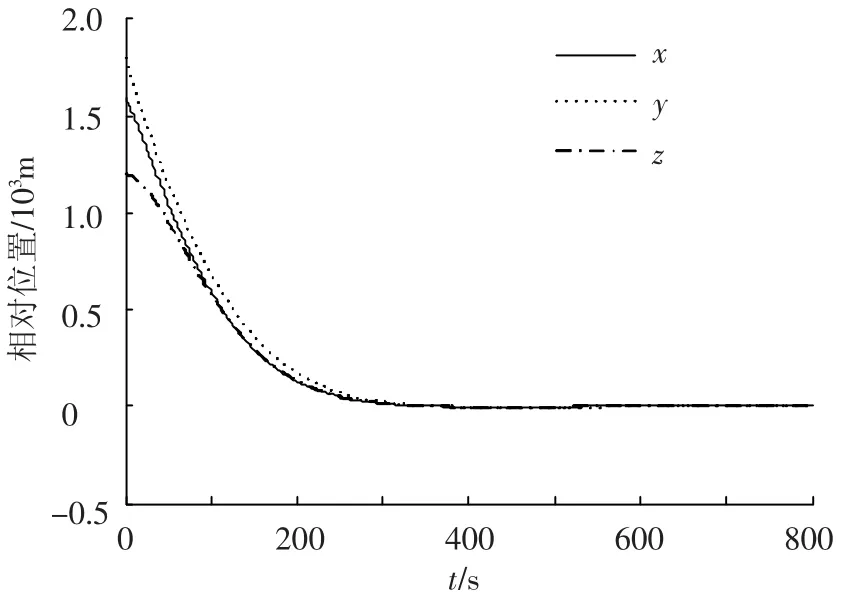
圖1 相對(duì)參考坐標(biāo)系下的相對(duì)位置

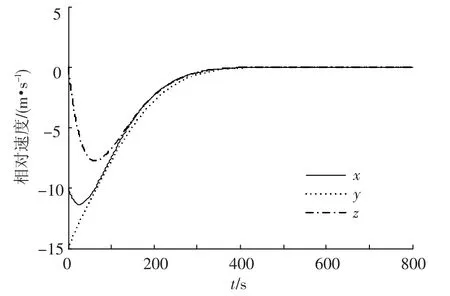
圖2 相對(duì)參考坐標(biāo)系下的相對(duì)速度

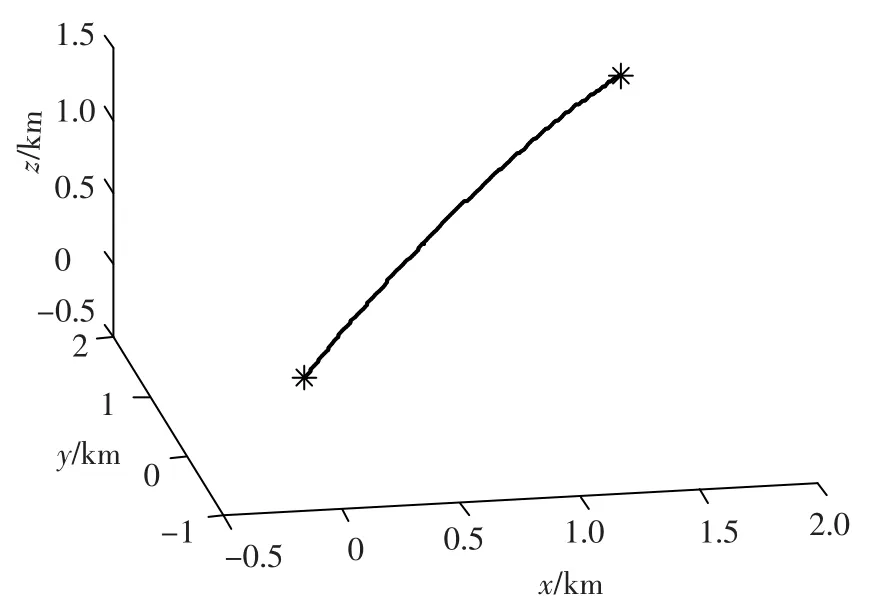
圖3 相對(duì)參考坐標(biāo)系下的攔截軌道

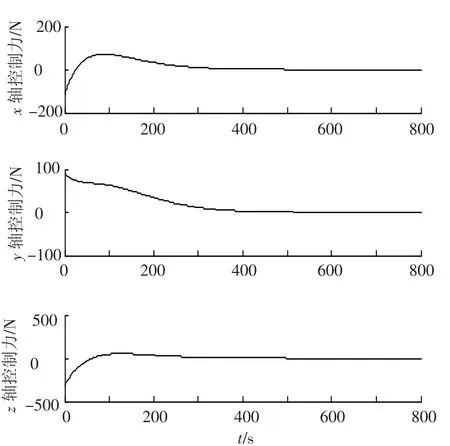
圖4 三軸控制力輸入曲線

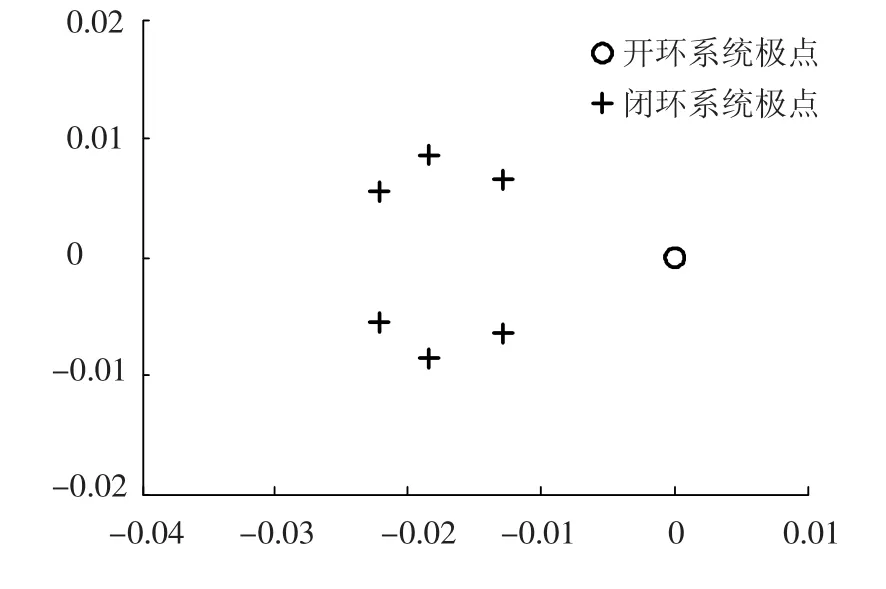
圖5 開(kāi)環(huán)系統(tǒng)和閉環(huán)系統(tǒng)極點(diǎn)示意圖

為進(jìn)一步驗(yàn)證本文控制器設(shè)計(jì)方法對(duì)不確定系統(tǒng)的適用性，在仿真中，令目標(biāo)衛(wèi)星軌道角速度的不確定度幅值為1=0.5，攔截衛(wèi)星質(zhì)量的不確定度幅值為2=0.5，其它參數(shù)不變.結(jié)果表明，相對(duì)位置和相對(duì)速度依然快速收斂并穩(wěn)定，500 s內(nèi)仍可分別收斂到10 m和0.1 m/s，800 s時(shí)控制精度分別為0.1 m和0.002 m/s.這說(shuō)明設(shè)計(jì)的控制器是有效的，并且對(duì)系統(tǒng)的不確定部分具有較好的魯棒性.

為說(shuō)明參數(shù)不確定性對(duì)閉環(huán)系統(tǒng)性能的影響，在本文控制器設(shè)計(jì)時(shí)不考慮參數(shù)的不確定性，且在其他約束條件和仿真條件不變的情況下，可計(jì)算控制增益陣為

在該控制器下，相對(duì)位置和相對(duì)速度的仿真結(jié)果如圖6和圖7所示，其動(dòng)態(tài)收斂過(guò)程的性能差于圖1和圖2，且800 s時(shí)控制精度分別為1.7 m和0.03 m/s.可見(jiàn)，若不考慮參數(shù)不確定性，將會(huì)影響閉環(huán)系統(tǒng)的動(dòng)態(tài)特性且控制精度底，從而說(shuō)明了本文算法對(duì)參數(shù)不確定系統(tǒng)的有效性.

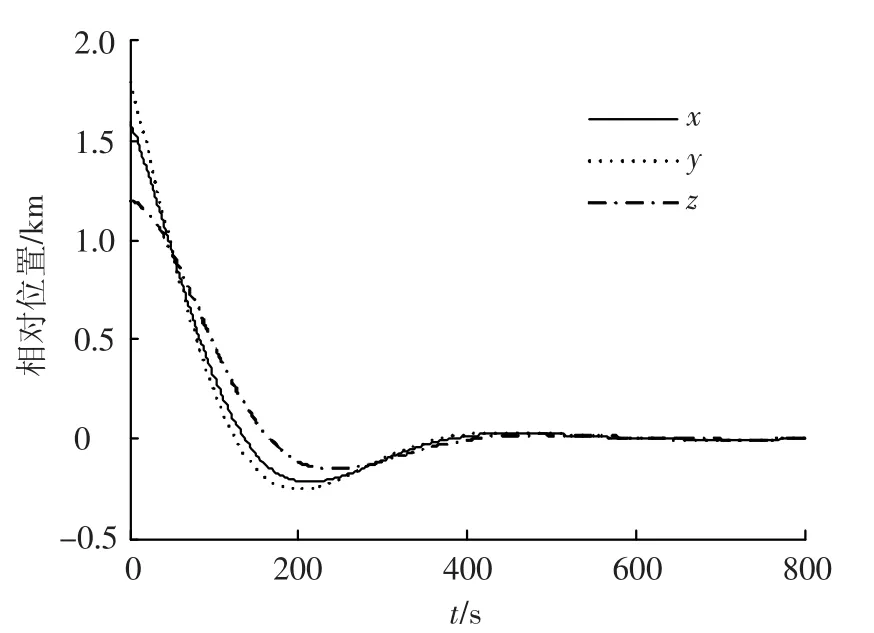
圖6 不考慮參數(shù)不確定性時(shí)的相對(duì)位置

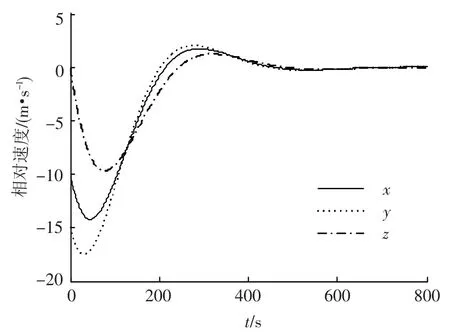
圖7 不考慮參數(shù)不確定性時(shí)的相對(duì)速度

4 結(jié)論

1)本文針對(duì)攔截衛(wèi)星的軌道攔截任務(wù)，考慮了多約束條件和系統(tǒng)有限時(shí)間二次型性能指標(biāo)的優(yōu)化，提出了一種基于LMI的軌道控制器設(shè)計(jì)方法.仿真結(jié)果表明，在系統(tǒng)模型存在不確定參數(shù)時(shí)，本文設(shè)計(jì)的控制器能夠使系統(tǒng)穩(wěn)定，并且能在獲得最優(yōu)系統(tǒng)有限時(shí)間性能的同時(shí)滿足控制輸入限幅和極點(diǎn)區(qū)域限制.由于本文設(shè)計(jì)的控制器采用的是狀態(tài)反饋控制，其結(jié)構(gòu)簡(jiǎn)單，因而便于工程應(yīng)用.

2)本文對(duì)系統(tǒng)的有限時(shí)間二次型性能指標(biāo)進(jìn)行了優(yōu)化.但由于攔截衛(wèi)星任務(wù)的特殊性，需要進(jìn)一步研究系統(tǒng)在有限時(shí)間內(nèi)的穩(wěn)定問(wèn)題.因此，下一步的工作是基于LMI方法設(shè)計(jì)控制器，使系統(tǒng)在有限時(shí)間穩(wěn)定并滿足多約束條件.

［1］周克強(qiáng)，高曉光，白奕.反衛(wèi)星衛(wèi)星攻擊方式研究［J］.飛行力學(xué)，2006，24(4):80－83.

［2］SINGLA P，SUBBARAO K，JUNKINS J L.Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty［J］.Journal of Guidance，Control，and Dynamics，2006，29(4):892 －902.

［3］GAO Huijun，YANG Xuebo，SHI Peng.Multi-objective robust H∞control of spacecraft rendezvous［J］.IEEE Transactions on Control Systems Technology，2009，17(4):794－802.

［4］TIWARI A，F(xiàn)UNG J，CARSON J M，et al.A framework for Lyapunov certificates for multi-vehicle rendezvous problems［C］//Proceedings of American Control Conference.Boston:［s.n.］，2004:5582 －5587.

［5］EBRAHIMI B，BAHRAMI M，ROSHANIAN J.Optimal sliding-mode guidance with terminal velocity constraint for fixed-interval propulsive maneuvers［J］.Acta Astronautica，2008，60(10):556－562.

［6］佘志坤，薛白，叢源良，等.最優(yōu)雙沖量交會(huì)問(wèn)題的數(shù)學(xué)建模與數(shù)值求解［J］.宇航學(xué)報(bào)，2010，31(1):155－161.

［7］TEBBANI S，ISABELLE Q，JACQUES B.Optimal finite thrust rendezvous using beneficial effects of the earth oblateness［J］.Astronautical Sciences，2002，109:2497－2508.

［8］GOODSON T，CHUANG J C H，HANSON J.Optimal finite thrust orbit transfers with large numbers of burns［J］.Journal of Guidance，Control，and Dynamics，1999，22(1):139－148.

［9］劉麗麗，文浩，金棟平，等.繩系衛(wèi)星軌道轉(zhuǎn)移的最優(yōu)控制［J］.航空學(xué)報(bào)，2009，30(2):332－336.

［10］李四平，劉錦陽(yáng)，國(guó)鳳林，等.軌道機(jī)動(dòng)的時(shí)間能量綜合最優(yōu)控制［J］.宇航學(xué)報(bào)，2010，31(1):137－142.

［11］沈毅，劉皓.基于時(shí)滯不確定理論的導(dǎo)彈魯棒控制系統(tǒng)設(shè)計(jì)［J］.航空學(xué)報(bào)，2011，32(3):473－479.

［12］PENG S，BOUKAS E K.On H∞control design for singular continuous-time delay systems with parametric uncertainties［J］.Journal of Nonlinear Dynamics and Systems Theory，2004，4(1):59－71.

［13］YUE Xincheng，YANG Ying，GENG Zhiyong.Indirect optimization for finite-thrust time-optimal orbital maneuver［J］.Journal of Guidance，Control and Dynamics，2010，33(2):628－634.

［14］涂良輝，袁建平，羅建軍.基于偽光譜方法的有限推力軌道轉(zhuǎn)移優(yōu)化設(shè)計(jì)［J］.宇航學(xué)報(bào)，2008，29(4):1189－1193.

［15］YANG Xuebo，BO Yuming，LIU Yurong，et al.Output tracking control for autonomous spacecraft rendezvous［C］//IEEE Conference on Decision and Control.Piscatawary:IEEE，2009:5227－5232.

［16］俞立.魯棒控制——線性矩陣不等式［M］.北京:清華大學(xué)出版社，2002:8－9.

［17］YANG Xuebo，GAO Huijun，SHI Peng.Robust orbital transfer for low earth orbit spacecraft with small-thrust［J］.Journal of the Franklin Institute，2010，347(10):1863－1887.

Finite time optimal control for non-cooperative targets rendezvous with multi-constraints

DENG Hong，SUN Zhao-wei，ZHONG Wei-chao，CHEN Chang-chun

(Research Center of Satellite Technology，Harbin Institute of Technology，150001 Harbin，China)

This paper studies the problem of orbit control for intercepting satellite based on state feedback control considering parametric uncertainties，finite time performance，control input constraint and poles assignment.The sufficient condition of controller is derived by Lyapunov approach，and then the controller design is transformed into a convex optimization problem in terms of linear matrix inequality.An illustrative example shows that the system is asymptotically stable with the designed controller and the optimal performance is obtained with control input and poles assignment constraints.

orbit control;uncertainty;finite time performance;control input constraint;poles assignment

V448.234

A

0367－6234(2012)11－0020－07

2011－10－09.

鄧 泓(1986—)，女，博士研究生;

孫兆偉(1963—)，男，教授，博士生導(dǎo)師.

鄧 泓，denghong@yeah.net.

(編輯 張 宏)