粒子濾波在衛星姿態確定中的應用
張 健,孫兆偉
(哈爾濱工業大學衛星技術研究所,150001 哈爾濱)
粒子濾波在衛星姿態確定中的應用
張 健,孫兆偉
(哈爾濱工業大學衛星技術研究所,150001 哈爾濱)
為了驗證以星敏感器和速率陀螺作為衛星測量元件時,粒子濾波算法在姿態確定中的有效性.采用修正的羅德里格參數作為姿態參數建立了有陀螺和無陀螺兩種模式下的系統狀態方程和測量方程,并利用粒子濾波(PF)算法進行了姿態估計.和擴展的卡爾曼濾波(EKF)算法進行比較,仿真結果表明:PF算法在小初始估計誤差下能夠收斂,且具有和EKF相當的精度.大初始估計誤差時,EKF算法不能收斂而PF算法仍能收斂.最后驗證了PF算法在無陀螺模式下進行姿態確定的有效性.
粒子濾波;姿態確定;星敏感器;速率陀螺
衛星姿態確定系統作為控制的前提,其精度直接影響到姿態控制的質量.目前,EKF算法作為非線性濾波的經典算法,在衛星姿態確定中被廣泛的應用.然而,EKF算法需要對非線性的狀態方程和測量方程進行線性化,并需要計算雅克比行列式,計算復雜魯棒性低.粒子濾波算法是基于貝葉斯最優估計理論和蒙特卡洛積分原理來對狀態的后驗概率密度函數進行近似,能夠克服EKF 的缺點[1-3].程楊等[4]利用粒子濾波算法,結合修正的羅德里格參數對衛星姿態進行估計,克服了四元數用于姿態估計時需要滿足四元數歸一化的約束問題,引入變化的協方差矩陣,克服了由于觀測誤差很小引起的樣本快速枯竭的問題.Oshman等[5]將粒子濾波算法和遺傳算法相結合,用于有陀螺工作下的衛星姿態確定,其算法結合了遺傳算法和例子濾波算法,雖然濾波精度有所提高,但計算量很大.姜雪原等[6]把 Rao-Blackwellization技術和粒子濾波結合,提出基于Marginalized的粒子濾波算法,并用于衛星姿態估計,取得了較好的效果.本文采用由Gordon等[7]提出的Bootstrap粒子濾波(BF)算法,對衛星的姿態確定問題進行了仿真研究,并針對有陀螺模式下粒子濾波算法出現的樣本枯竭問題,對粒子濾波進行改進,引入擴展的卡爾曼粒子濾波(EKPF)算法,結果證明其可行性.最后利用粒子濾波算法對無陀螺模式下的姿態確定問題進行了仿真分析,驗證了其有效性.
1 系統狀態方程
本文針對有陀螺和無陀螺兩種模式,采樣修正的羅德里格參數作為狀態參數,分別建立了系統的狀態方程.
假設衛星為一單剛體,則用修正的羅德里格參數表示的運動學方程為
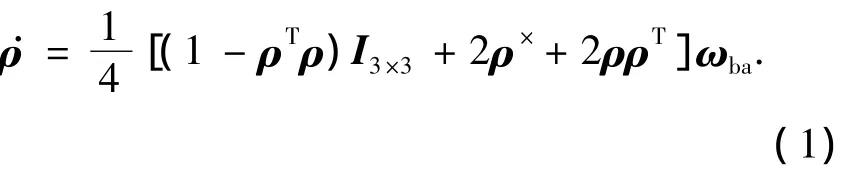
式中:ρ = [ρx,ρy,ρz]T為修正的羅德里格參數;I3×3為3階的單位陣;ωba為體系相對于參考系的角速度;ρ×為ρ的叉乘矩陣,表示為
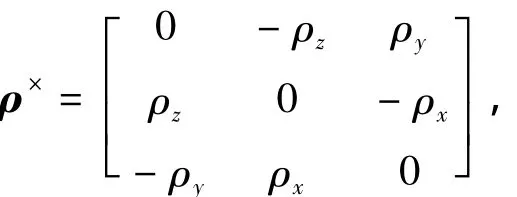
動力學方程為
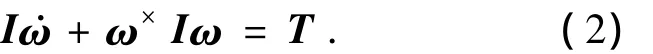
式中:I為衛星在星體固聯坐標系的轉動慣量矩陣;T為作用在星體上的內外力矩的分量列陣.
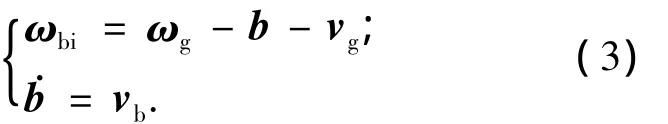
陀螺測量模型采用簡單的Farrenkopf模型,可表示為式中:ωbi為衛星相對于慣性空間的旋轉角速度;ωg為陀螺測量的角速度;b為陀螺常值漂移;vg為陀螺測量的白噪聲,滿足vg~N(0,σ2g);vb為驅動陀螺常值漂移的白噪聲,滿足vb~N(0,σ2b).
1.1 有陀螺模式下的狀態方程
有陀螺模式下選擇修正的羅德里格參數和陀螺漂移作為狀態變量,即
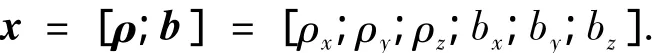
式中:b= [bx,by,bz]T為陀螺漂移.則根據方程(1)和(3)可得系統的狀態方程為
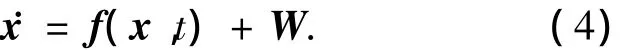
式中:W為系統噪聲,這里假設為零均值的高斯噪聲,f(x,t)為非線性函數,有
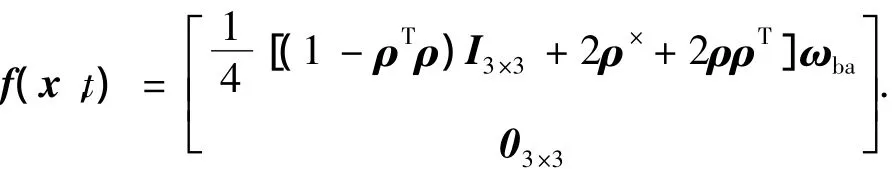
1.2 無陀螺模式下的狀態方程
無陀螺模式下用衛星動力學方程來代替陀螺測量方程,選擇修正的羅德里格參數和角速度作為狀態變量,即則根據方程(1)和方程(2)可得系統的狀態方程為方程(4)表示的形式,其中f(x,t)為
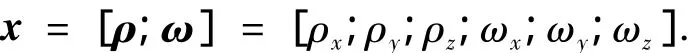
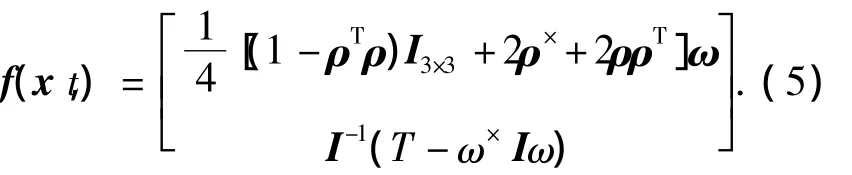
2 測量方程
星敏感器是一種以恒星為姿態參考的高精度光學敏感器,是航天器姿軌控系統中常用到的敏感元器件.由筒鏡光學系統和CCD面陣光敏元器件組成,來自星光的平行光經過光學系統,在CCD面陣上聚焦成像圈[8].如圖1所示,定義星敏感坐標系Oxsyszs,zs軸沿中心光軸,xs和 ys軸沿CCD面陣的正交基準,(px,py)為星光像元在面內的坐標,f為光學系統的焦距.
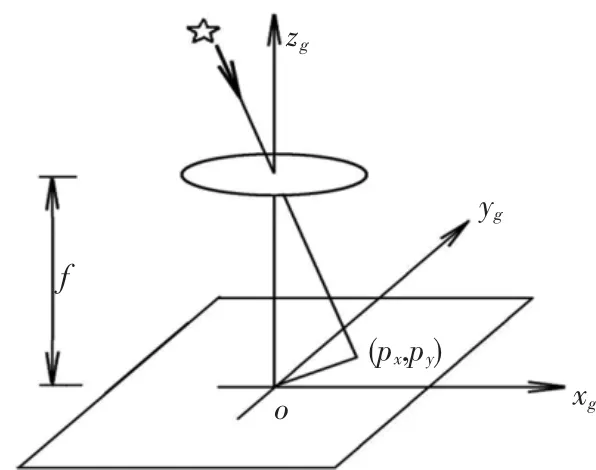
圖1 星敏感器測量原理圖
假設星敏感器坐標系與星體坐標系重合,且光軸沿星體zb軸方向.用p=[px;py]表示星光矢量ri在CCD平面上成像點的真實坐標,記為
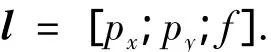
定義慣性空間中相對于某個恒星天體的兩個平行的參考矢量的觀測值分別為ui1和ui2,則可以建立星敏感器的測量模型為
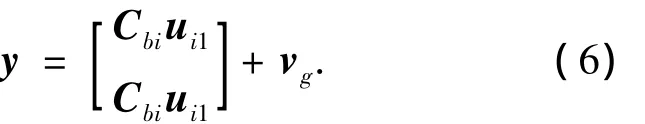
式中:Cbi為慣性系到體系的坐標變換矩陣;vg為星敏感器的測量噪聲.為便于分析,采用:ui1=[1,0,0]T,ui1= [0,1,0]T.
3 粒子濾波算法在姿態確定中的應用
所謂粒子濾波是指:通過尋找一組在狀態空間中傳播的隨機樣本,對概率密度函數p(xk|zk)進行近似,以樣本均值代替積分運算,從而獲得狀態的最小方差估計的過程,是一種基于貝葉斯估計思想的非線性濾波算法.當粒子數目足夠大時,這些樣本點能非常接近地表征后驗概率密度.
Gordon等人提出 Bootstrap粒子濾波算法(BF),由于應用簡單得到了廣泛應用,其基本步驟如下:
1)初始化.從p(x0)中隨機抽取N個樣本,xi0~ N(0,^P(x0)),wi0=1/N,i=1,2,…,N,其中N為粒子數.
2)遞推計算,k=1,2,….
3)重要性抽樣,從q(xk|xk-1,zk)中隨機抽取N個樣本,利用公式(7)計算權值,并利用公式(8)進行歸一化,
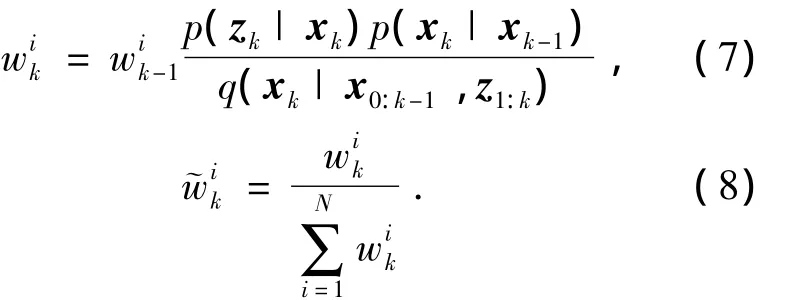
4)重采樣.由公式(9)計算有效粒子數[10],并與預定的閥值粒子數比較判斷是否需要進行重采樣.若Neff<Nth,則進行重采樣;其中Nth為重采樣的閥值粒子數,取Nth=2/3N,否則轉步驟5;
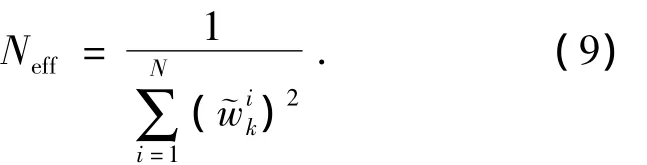
5)輸出估計值.BF粒子濾波算法采用的重要性函數是次優的,并且沒有充分利用當前的測量信息.為得到更為精確的重要性函數,在粒子一步更新階段引入EKF過程,通過EKF對所有粒子進行一步更新,在加權求均值和協方差,即得到擴展的卡爾曼粒子濾波(EKPF).EKPF算法和BF算法相比,在粒子更新階段充分利用了當前的測量信息,能得到更好的估計效果[11].這里采用修正的羅德里格參數作為衛星姿態參數,和四元數相比,沒有約束條件,其協方差矩陣非奇異[12].根據有陀螺和無陀螺兩種模式下得到的狀態方程和測量方程,選擇不同的狀態估計初值和協方差矩陣,利用上述的粒子濾波算法進行狀態估計.
4 數學仿真
模式一:
有陀螺模式,仿真參數為
1)假設衛星星體處于沒有控制力矩,只受到外界干擾力矩作用的狀態,仿真過程中假設外加的干擾力矩矢量為 Td= [10-5;10-5;10-5]N·s;
假設衛星星體的轉動慣量矩陣為I=diag(100,200,200)kg·m2;
2)姿態角和角速度初值分別為φ=0°,θ=0°,Ψ =0°;wx0=0(°)/s,wy0=0(°)/s,wz0=0(°)/s;
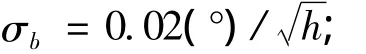
4)星敏感器測量噪聲的均方差為σp=100 urad;星敏感器的采樣周期為1 Hz;仿真步長取1 s.
估計初值:①小初始估計誤差:姿態角估計值設為[1,1,1]°,陀螺漂移估計值設為[2,2,2](°)/h,姿態方差為(1°)2,初始陀螺漂移的方差為(1(°)/h)2,采樣粒子數為1 000;②初始的姿態角初值設為[12,-10,170]°,其他同上;由圖 2可知,在小初始估計誤差情況下使用粒子濾波算法,姿態角估計估計誤差能夠收斂,但陀螺漂移估計誤差不能夠收斂,而是在初值附近的某個值上下波動.這是因為陀螺漂移的遞推過程是一個靜態的傳播過程,即bk+1=bk,這樣在粒子濾波過程中經過幾次重采樣過程后,所有粒子點幾乎全部集中在一個粒子上,造成樣本枯竭現象,達不到濾波效果.

圖2 陀螺模式下小初始估計誤差PF姿態角誤差和陀螺漂移估計誤差曲線
由圖3可知,用EKPF算法對小初始估計誤差的情況狀態進行估計,姿態角和角速度的收斂精度分為 0.002°和 0.000 05(°)/s.說明在小初始估計誤差的情況下,EKPF算法和EKF算法都能夠收斂,具有相同的精度.但EKPF算法計算量大,不適合用于實時狀態估計.
由圖4和圖5可知,在大初始估計誤差的情況下,EKPF算法還能保持收斂,但EKF算法就變得發散了.這也體現了EKPF算法在狀態估計中的優勢.
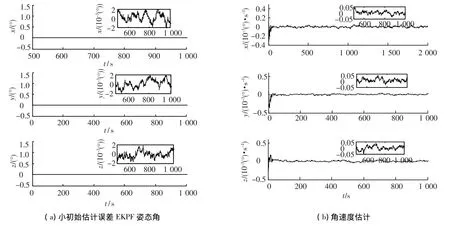
圖3 有陀螺模式下小初始估計誤差EKPF姿態角和角速度估計誤差曲線
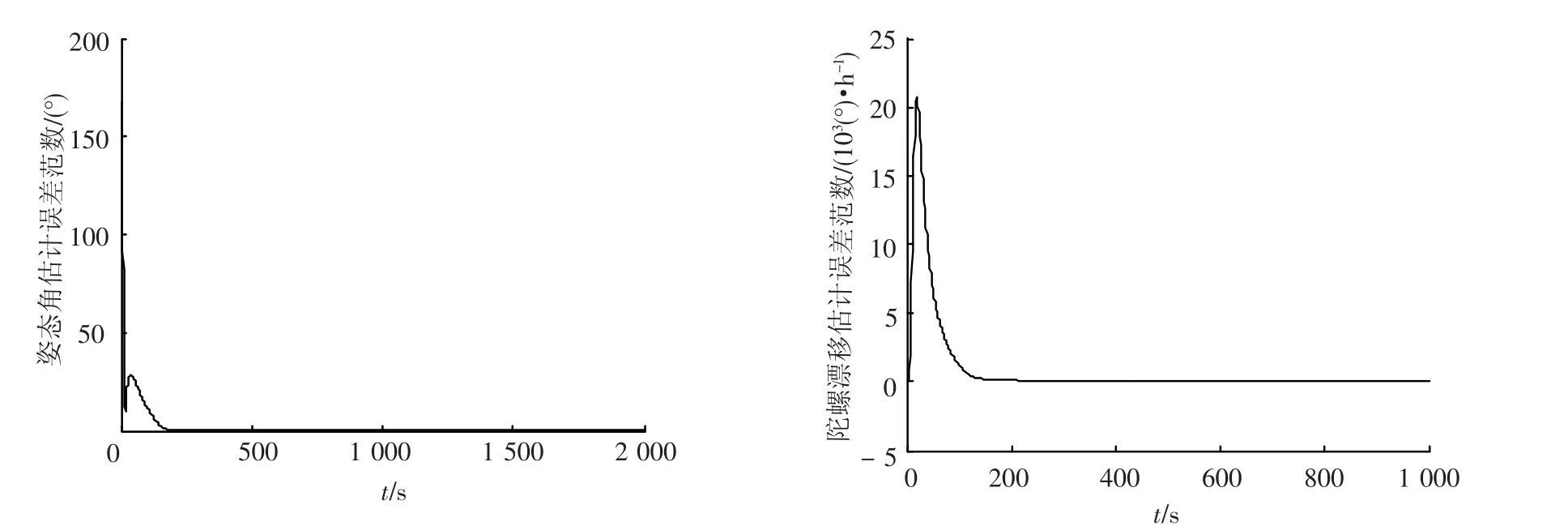
圖4 有陀螺模式下大初始估計誤差EKPF姿態角和陀螺漂移估計誤差范數曲線
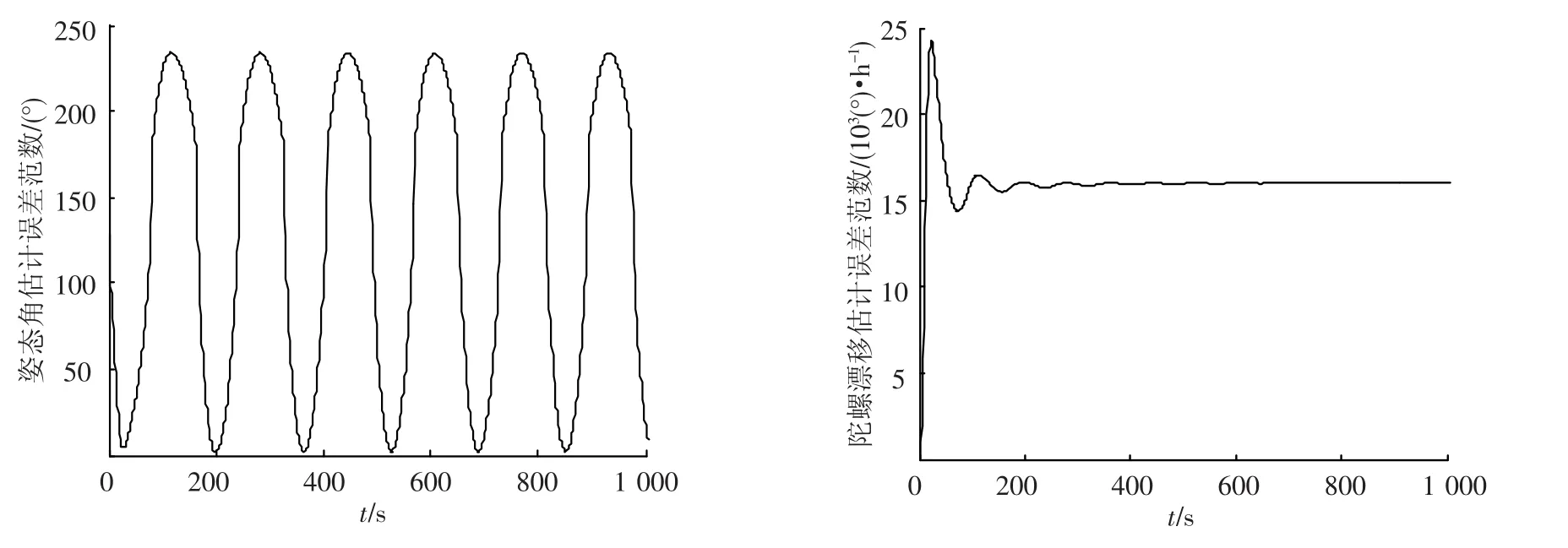
圖5 有陀螺模式下大初始估計誤差EKF姿態角和陀螺漂移估計誤差范數曲線
模式二:無陀螺模式
仿真參數為:姿態角估計值設為[1,1,1]°,角速度估計初值設為[0.001,0.001,0.001](°)/s,姿態方差為(1°)2,角速度的方差為(0.001(°)/s)2,采樣粒子數為1 000,其他同有陀螺模式下得仿真參數設置.
圖6表明,粒子濾波在無陀螺模式下,姿態角估計精度為0.01°,角速度估計精度為0.004(°)/s,雖然和有陀螺時相比,精度降低,但仍能滿足一般精度要求的衛星.
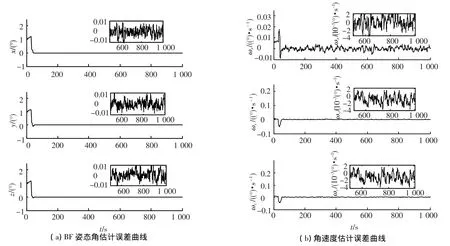
圖6 無陀螺模式下BF姿態角和角速度估計誤差曲線
5 結論
本文對粒子濾波算法及其在衛星姿態估計中的應用進行了研究.結果表明:在有陀螺模式下,當直接使用粒子濾波算法時,由于重采樣過程引起了樣本枯竭,陀螺漂移不能收斂;為此采用EKPF算法,可以緩解樣本枯竭的現象,姿態角和陀螺漂移都可以收斂,且具有和EKF算法相同的估計精度.另外,采用粒子濾波算法的優勢主要體現在初始估計誤差較大的情況下,估計結果仍然可以收斂.最后,在無陀螺情況下,用衛星動力學模型代替陀螺測量模型,結果表明仍能達到一定精度的估計精度,適用于一般精度要求的衛星姿態確定.
[1]MOHD POINT KEUI A A,FADLY M,SIDEK O.EKF implementation on S3CEV40 for Inno SAT attitude determination system[C]//2011 Internation Conference on Computer Applications and Industrial Electronics,Penang,MALAYSIA:IEEE,[s.n.],2011:373 -378.
[2]HUANG Guoquan P.MOURIKIS A I,ROUMELITIOTIS S I.A First-Estimates Jacobian EKF for improving SLAM Consistency[C]//Proceedings of the International Symposium on Experimental Robotics(ISER),Athens,Greece:[s.n.],2008:373 -382.
[3]SOKEN H E,HAJIYEV C.REKF and RUKF development for pico satellite attitude estimation in the presence of measurement faults[C]//Recent Advances in Space Technologies(RAST),2011 5th International Conforence on,Istanbul:IEEE,2011:891-896.
[4]CHENG Y,CRASSIDIS J.Particle filtering for sequential spacecraft attitude estimation[C]//AIAA Guidance,Navigation,and Control Conference and Exhibit,Providence,American Intstitute of Aeronautics and Astronautics.Rhode,Island:[s.n.],2004:2004 -5337.
[5]OSHMAN Y,CARMI A.Spacecraft attitude estimation from vector observations using a fast particle filter[J].Advances in the Astronautical Sciences,2005,Suppl 119:593-607.
[6]姜雪原,馬廣福,胡慶雷.基于Marginalized粒子濾波的衛星姿態估計算法[J].控制與決策,2007,22(1):39-44.
[7]GORDON N,SALMOND D.Novel approach to non-linear and non-gaussian Bayesian state estimation [J].Proceedings of Institude Electric Engineering,1993,40(2):107-113.
[8]孫兆偉,李暉,張世杰.僅用星敏感器的衛星姿態估計UKF算法研究[J].飛行力學,2006,24(3):56-60.
[9]LIU J S,CHEN R.Sequential monte carlo methods for dynamic system[J].Journal of the American Statistical Association,1998,443(93):1032-1044.
[10]王晨,房建成.基于Unscented四元數粒子濾波的微小衛星姿態估計[J].北京航天航空大學學報,2007,33(5):552-556.
[11]牟忠凱,隋立芬,黃賢源.基于UPF的修正的羅德里格參數衛星姿態估計[J].中國空間科學技術,2009,29(6):45-50.
Satellite attitude determination based on particle filter
ZHANG Jian,SUN Zhao-wei
(Research Center of Satellite Technology,Harbin Institute of Technology,150001 Harbin,China)
In order to investigate the efficiency of attitude determination system using particle filter.The system state equation and measure equation of a satellite with star-sensors and gyros were established.And particle filter was used to estimate the attitude of satellite.The simulation results showed that the system can convergent not only for the small initial estimation error,but also for the big initial estimation error.But EKF can convergent only for the small initial estimation error.Finally,the effectiveness of PF applied to the gyro-free mode was also verified.
particle filter;attitude determination;star-sensor;rate gyro
V19
A
0367-6234(2012)11-0031-05
2012-02-13.
張 健(1988—),男,碩士研究生;
孫兆偉(1963—),男,教授,博士生導師.
張 健,zhangjian6140@126.com.
(編輯 苗秀芝)

