基于GA-RBF神經(jīng)網(wǎng)絡(luò)逆的兩電機(jī)同步控制
康 梅,趙文祥,吉敬華,劉國(guó)海
(江蘇大學(xué),江蘇鎮(zhèn)江212013)
0引 言
隨著多電機(jī)變頻調(diào)速系統(tǒng)在造紙、電動(dòng)汽車、軌道交通等領(lǐng)域越來(lái)越廣泛的應(yīng)用,高性能的同步協(xié)調(diào)控制成為亟待解決的技術(shù)難題。國(guó)內(nèi)外學(xué)者對(duì)多電機(jī)系統(tǒng)中速度和張力的解耦控制進(jìn)行了一系列的研究[1-4]。其中,將逆系統(tǒng)與神經(jīng)網(wǎng)絡(luò)相結(jié)合的神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法[5-8],從控制算法入手,結(jié)合兩者優(yōu)勢(shì),實(shí)現(xiàn)了對(duì)一般非線性系統(tǒng)的線性化和解耦控制,最近幾年來(lái)成為提升被控系統(tǒng)控制性能的一種新方法。但已有在訓(xùn)練神經(jīng)網(wǎng)絡(luò)時(shí),存在著收斂速度慢、甚至?xí)斐删W(wǎng)絡(luò)發(fā)散,且不易得到全局最優(yōu)值以及結(jié)構(gòu)和類型的選擇過(guò)分依賴經(jīng)驗(yàn)等缺陷。系統(tǒng)輸入輸出之間映射關(guān)系不能很好地被反映,大大降低網(wǎng)絡(luò)的逼近性能。本文結(jié)合徑向基函數(shù)(Radial Basis Function,RBF)神經(jīng)網(wǎng)絡(luò)[9-10]和遺傳算法(Genetic Algorithm,GA)的思想[11-12],提出一種基于遺傳算法優(yōu)化的RBF神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)的兩電機(jī)同步控制方法。遺傳算法是模仿生物遺傳學(xué)和自然選擇機(jī)理,通過(guò)人工方式構(gòu)造的一類優(yōu)化搜索算法。遺傳算法具有魯棒性強(qiáng)、搜索范圍廣、搜索效率高的特點(diǎn)。運(yùn)用遺傳算法訓(xùn)練RBF神經(jīng)網(wǎng)絡(luò)無(wú)需先驗(yàn)知識(shí),對(duì)初始參數(shù)不敏感,不會(huì)陷入局部極小點(diǎn)。實(shí)驗(yàn)證明該方法能實(shí)現(xiàn)兩電機(jī)速度和張力的解耦控制,而且有實(shí)時(shí)性好,響應(yīng)速度快,魯棒性強(qiáng)等優(yōu)點(diǎn)。
1兩電機(jī)同步系統(tǒng)的可逆性問(wèn)題
圖1為速度和張力控制的兩電機(jī)同步系統(tǒng)物理模型。
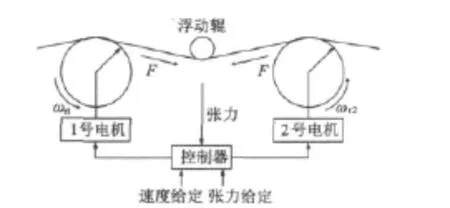
圖1 兩電機(jī)同步控制示意圖
根據(jù)力學(xué)彈性理論中的胡克定律,張力如下:
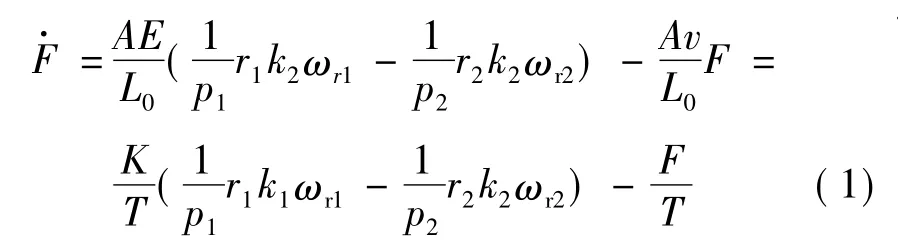
變頻器采用矢量控制方式,忽略變頻器的電流滯后時(shí)間常數(shù),兩電機(jī)同步系統(tǒng)的模型簡(jiǎn)化:
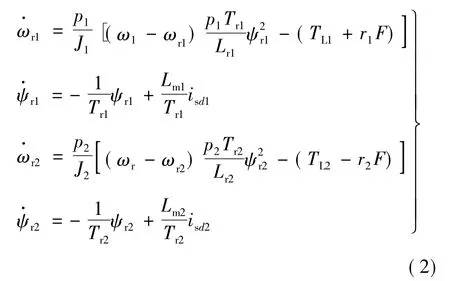
式中:F為皮帶之間的張力;A為皮帶的截面積;r為電機(jī)皮帶輪半徑;k為皮帶輪速比;K為傳遞系數(shù);T為張力變化常數(shù);ωr為轉(zhuǎn)子速度;p為電機(jī)極對(duì)數(shù);v為期望的轉(zhuǎn)速;E為皮帶的彈性楊氏模量;L0為兩電機(jī)支架間的距離;ω為電機(jī)同步角速度;ψr為轉(zhuǎn)子磁鏈;J為轉(zhuǎn)動(dòng)慣量;TL為負(fù)載轉(zhuǎn)矩;Tr為電機(jī)時(shí)間常數(shù);Lr為轉(zhuǎn)子電感;Lm為轉(zhuǎn)子和定子間的互感。式中下標(biāo)的1,2代表第1,2臺(tái)電機(jī)。
對(duì)于式(1)、式(2)中的電機(jī)模型而言,其磁通子系統(tǒng)是線性的,在不考慮磁通變化的情況下,可將其改成為:
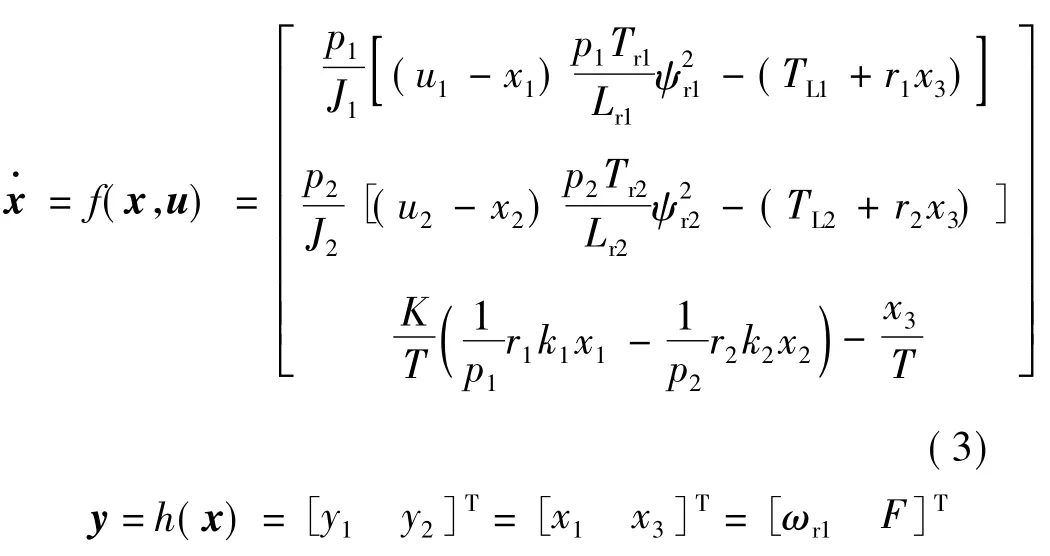
式(3)狀態(tài)變量:
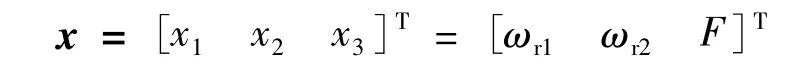
控制變量:
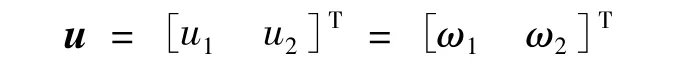
對(duì)輸出求導(dǎo)后,得:
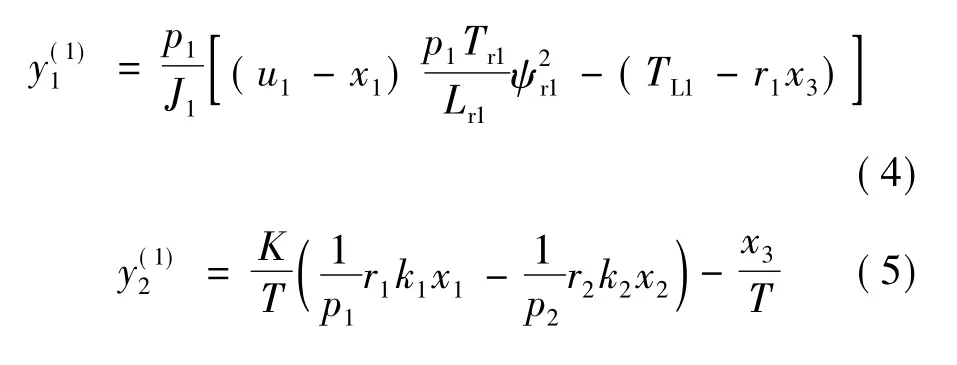
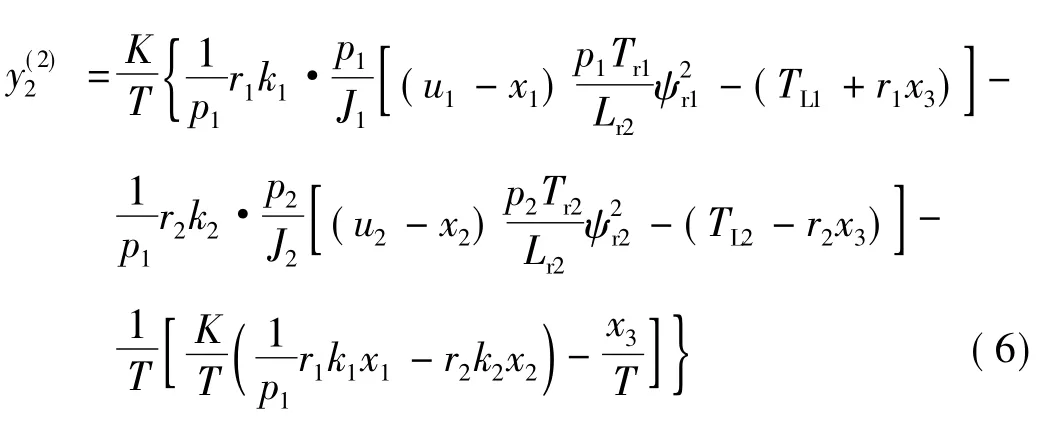
則Jacobi矩陣:
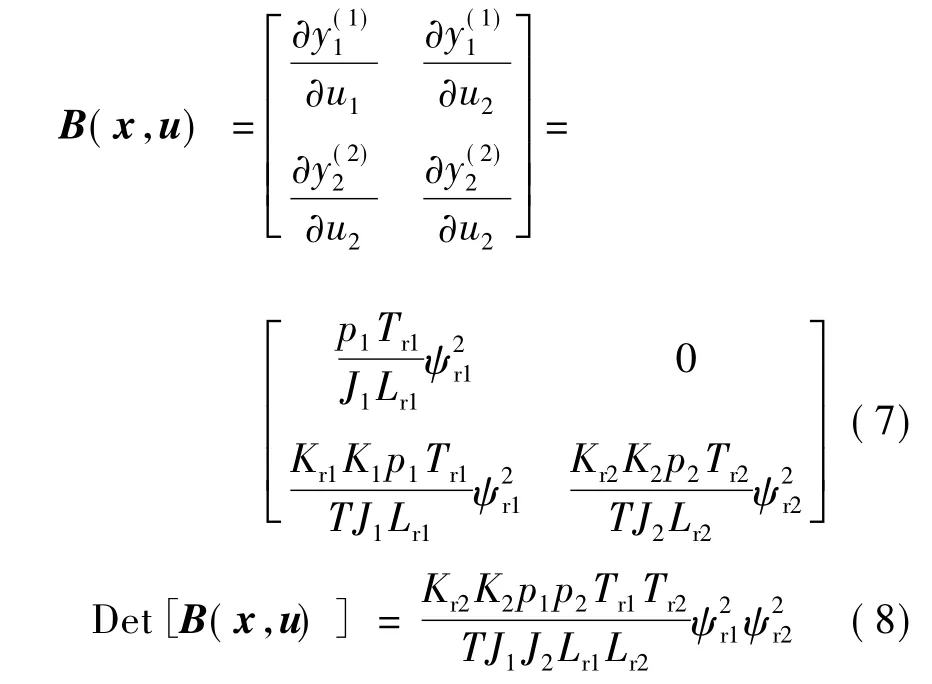
當(dāng) ψr1與 ψr2均不為零時(shí),B(x,u)的行列式亦非零,即為非奇異矩陣。系統(tǒng)的相對(duì)階數(shù)為?=(1,2),即?1+?2=3<n。因此可知,此兩電機(jī)同步系統(tǒng)可逆。復(fù)合被控系統(tǒng)由被控系統(tǒng)與兩電機(jī)同步系統(tǒng)相串聯(lián)構(gòu)成,此時(shí)被控系統(tǒng)是線性的,且被解耦成速度和張力兩個(gè)獨(dú)立的子系統(tǒng)。
2 GA-RBF神經(jīng)網(wǎng)絡(luò)逆控制
神經(jīng)網(wǎng)絡(luò)具有強(qiáng)大的自學(xué)習(xí)能力,只要隱層和隱層節(jié)點(diǎn)數(shù)足夠多,就可以實(shí)現(xiàn)任意從輸入到輸出的非線性映射。目前,BP網(wǎng)絡(luò)在神經(jīng)網(wǎng)絡(luò)算法中用的比較廣泛,但BP網(wǎng)絡(luò)在逼近能力、分類能力和學(xué)習(xí)速度等方面均遜于RBF網(wǎng)絡(luò),所以本文采用RBF網(wǎng)絡(luò)。鑒于神經(jīng)網(wǎng)絡(luò)易陷入局部最小、全局搜索能力弱等缺點(diǎn),遺傳算法具有高效全局尋優(yōu)能力,本文將神經(jīng)網(wǎng)絡(luò)和遺傳算法兩者相結(jié)合,構(gòu)成了GARBF神經(jīng)網(wǎng)絡(luò)。
2.1 RBF神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)
RBF神經(jīng)網(wǎng)絡(luò)采用輸入層、隱含層、輸出層三層結(jié)構(gòu),節(jié)點(diǎn)數(shù)依次為 5,7,2。設(shè) X=[x1,x2,x3,x4,x5],X 為網(wǎng)絡(luò)的輸入向量。
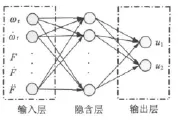
圖2 RBF神經(jīng)網(wǎng)絡(luò)結(jié)構(gòu)
其中RBF的隱含層采用通用的高斯函數(shù):
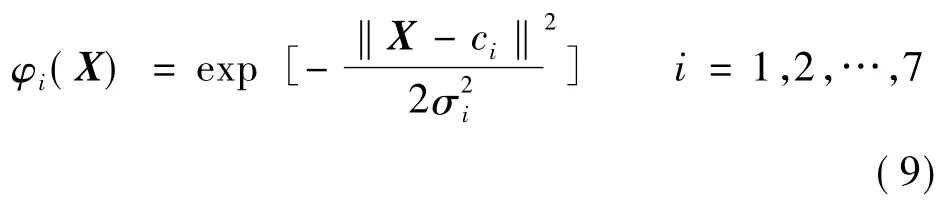
式中:ci為第i個(gè)隱層節(jié)點(diǎn)的中心;σi為第i個(gè)隱層節(jié)點(diǎn)的寬度。網(wǎng)絡(luò)輸出:
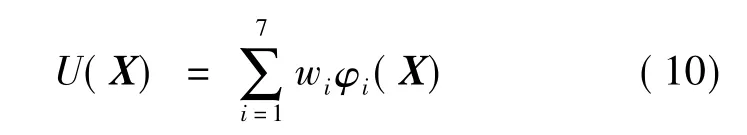
式中:wi為第i個(gè)隱層節(jié)點(diǎn)與輸出空間的連接權(quán)。
由以上分析可知,在RBF網(wǎng)絡(luò)中,需要確定的參數(shù)主要有隱含層的中心ci和寬度σi以及隱含層與輸出層之間的連接權(quán)值wi,這三個(gè)參數(shù)的取值影響著RBF神經(jīng)網(wǎng)絡(luò)性能的好壞。因此必須選擇合適的 ci、σi、wi,以提高 RBF 網(wǎng)絡(luò)性能。
2.2遺傳算法(GA)對(duì)RBF網(wǎng)絡(luò)的優(yōu)化
用于RBF網(wǎng)絡(luò)的學(xué)習(xí)算法有很多,但都存在一定的局限性。相比而言,在所有算法中,最有效的方法是遺傳算法。遺傳算法是模擬生物進(jìn)化論的自然選擇和遺傳學(xué)機(jī)理的生物進(jìn)化過(guò)程的計(jì)算模型。是一種通過(guò)模擬自然進(jìn)化過(guò)程搜索全局最優(yōu)解的方法。特點(diǎn)是直接對(duì)結(jié)構(gòu)對(duì)象進(jìn)行操作,不需要確定的規(guī)則和其他輔助信息,就能搜索到最優(yōu)參數(shù)[13]。本文采用GA遺傳算法的群體并行搜索和全局收斂最優(yōu)的能力,對(duì)RBF神經(jīng)網(wǎng)絡(luò)的隱層中心值、寬度值以及和輸出層之間的權(quán)值進(jìn)行優(yōu)化。
(1)染色體編碼
為了便于操作和提高精度,本文直接采用實(shí)數(shù)編碼,而未采用傳統(tǒng)的二進(jìn)制形式編碼。待優(yōu)化的RBF神經(jīng)網(wǎng)絡(luò)的每個(gè)參數(shù)用一個(gè)實(shí)數(shù)來(lái)表示,參數(shù)個(gè)數(shù)的總和即為碼串的長(zhǎng)度。編碼時(shí),先順序排列不同的中心值以及與之對(duì)應(yīng)的寬度,再將各個(gè)調(diào)節(jié)權(quán)重值順序排列。在重要算子的交叉作用下,同一個(gè)體的中心值以及與之對(duì)應(yīng)的寬度值同時(shí)變化的概率較高,容易實(shí)現(xiàn)寬度值隨著中心值的變化而變化的要求。對(duì)5個(gè)輸入量、7個(gè)隱層節(jié)點(diǎn)、2個(gè)輸出量的RBF神經(jīng)網(wǎng)絡(luò),徑向基函數(shù)隱層節(jié)點(diǎn)的中心參數(shù)、寬度參數(shù)以及隱層節(jié)點(diǎn)與輸出空間連接權(quán)組成的編碼串如下:c11,…,c15;c21,…,c25;…;c71,…,c75;σ1,…,σ7;w11,w21,…,w71;w12,w22,…,w72共 56 個(gè)參數(shù)(串長(zhǎng)=56)。
(2)產(chǎn)生初始種群
M個(gè)染色體串隨機(jī)產(chǎn)生,其取值一般介于50~100之間,本文中初始種群取為80。
(3)適應(yīng)度函數(shù)的選取
遺傳算法在進(jìn)化搜索中只以適應(yīng)度函數(shù)為依據(jù),很少利用其他信息。因而適應(yīng)度函數(shù)的選取與遺傳算法的收斂速度以及與能否找到最優(yōu)解密切相關(guān)。
為了能夠比較直觀地反映每個(gè)染色體性能的好與差,選取RBF網(wǎng)絡(luò)的期望輸出與實(shí)際輸出之差的絕對(duì)值的累加和的倒數(shù)作為適應(yīng)度函數(shù)[14]。即對(duì)第i個(gè)染色體,其適應(yīng)度:
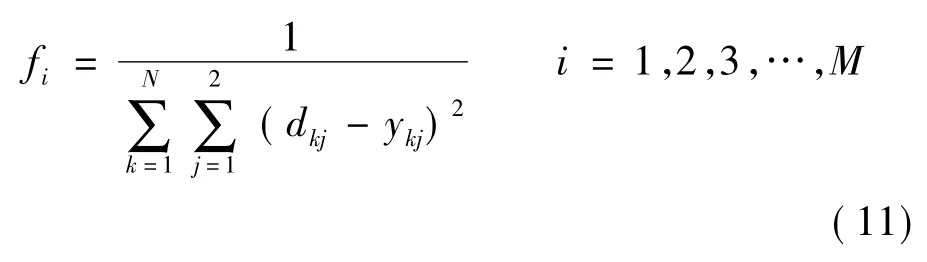
式中:N為訓(xùn)練樣本量;ykj為訓(xùn)練樣本的輸出實(shí)際值;dkj為訓(xùn)練樣本輸出的期望值;M為染色體串的初始種群值。fi與適應(yīng)度呈正相關(guān)關(guān)系。
(4)選擇操作
依據(jù)適應(yīng)度比例的方法,個(gè)體選擇的概率正比于適應(yīng)度值大小,即:
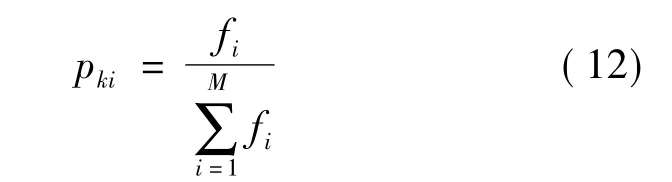
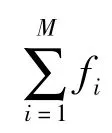
(5)自適應(yīng)變異和交叉操作
本文采取按位變異的方法進(jìn)行變異操作,兩點(diǎn)交叉法進(jìn)行交叉操作[15-16],為保持種群的多樣性,取變異和交叉的概率分別為pm和pc,如下式:
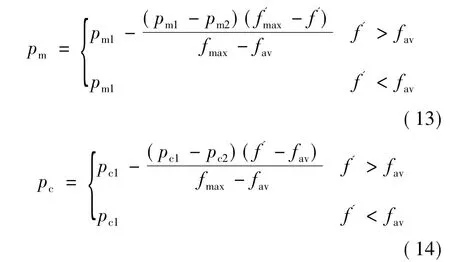
式中:f'為兩個(gè)待交叉的個(gè)體中適應(yīng)度較大的值;f為變異個(gè)體的適應(yīng)度值;fmax為群體中適應(yīng)度最大值;fav為每代群體的適應(yīng)度平均值。
2.3神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)的實(shí)現(xiàn)
用MATLAB軟件構(gòu)造神經(jīng)網(wǎng)絡(luò),使用輸入輸出樣本約6000組數(shù)據(jù)訓(xùn)練神經(jīng)網(wǎng)絡(luò),由于篇幅有限,略去具體值。將誤差指標(biāo)設(shè)在0.001。在遺傳算法優(yōu)化網(wǎng)絡(luò)參數(shù)中,群體初始大小為80,pc=0.6,pm=0.02,來(lái)獲得RBF神經(jīng)網(wǎng)絡(luò)的最優(yōu)控制參數(shù)。
將訓(xùn)練好的RBF神經(jīng)網(wǎng)絡(luò)逆系統(tǒng),串在兩電機(jī)同步系統(tǒng)之前,構(gòu)成復(fù)合被控系統(tǒng)。此時(shí)被控系統(tǒng)被解耦成兩個(gè)相對(duì)獨(dú)立的偽線性子系統(tǒng)。y=s-1·φ(s)為偽線性速度子系統(tǒng),y=s-2φ(s)為偽線性張力子系統(tǒng)。設(shè)計(jì)PI調(diào)節(jié)器整定速度偽線性子系統(tǒng),設(shè)計(jì)PD調(diào)節(jié)器整定張力偽線性子系統(tǒng),圖3為神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)控制的兩電機(jī)控制系統(tǒng)結(jié)構(gòu)示意圖。
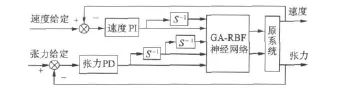
圖3 控制系統(tǒng)結(jié)構(gòu)示意圖
3實(shí)驗(yàn)驗(yàn)證
為驗(yàn)證理論分析的正確性,搭建了多電機(jī)實(shí)驗(yàn)系統(tǒng),如圖4所示。實(shí)驗(yàn)系統(tǒng)中籠型電機(jī)型號(hào)Y100L1-4,額定轉(zhuǎn)速1 420 r/min,額定功率2.2 kW,線電壓380 V,星型接法。硬件由西門子MMV變頻器、光電編碼器、12位高速模數(shù)轉(zhuǎn)換器—ADC7112、24位高速計(jì)數(shù)卡—PCL833以及與變頻器RS485接口連接的串行通訊卡—PCL745組成。運(yùn)用C++編寫(xiě)數(shù)據(jù)采樣程序與通訊程序,采用USS協(xié)議進(jìn)行通訊。
在兩電機(jī)實(shí)驗(yàn)系統(tǒng)上,變頻器工作在矢量控制方式狀態(tài),驗(yàn)證了神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法的控制效果。圖5是張力給定保持不變,對(duì)速度給定突加,采用GA-RBF神經(jīng)網(wǎng)絡(luò)控制器的張力和速度響應(yīng)曲線。圖6為速度給定保持不變,對(duì)張力給定突加,采用GA-RBF神經(jīng)網(wǎng)絡(luò)控制器的張力和速度響應(yīng)曲線。

圖4 多電機(jī)試驗(yàn)系統(tǒng)
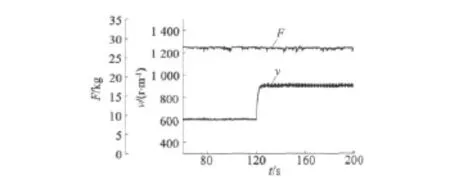
圖5 GA-RBF神經(jīng)網(wǎng)絡(luò)控制速度突加張力恒定響應(yīng)圖
上述實(shí)驗(yàn)結(jié)果驗(yàn)證了GA-RBF神經(jīng)網(wǎng)絡(luò)控制下的速度與張力的解耦效果。速度和張力在突變情況下,均未明顯影響對(duì)方的控制效果,滿足了兩電機(jī)系統(tǒng)的速度、張力解耦控制要求,系統(tǒng)的抗干擾性和魯棒性得到明顯提升。

圖6 GA-RBF神經(jīng)網(wǎng)絡(luò)控制張力突加速度恒定響應(yīng)圖
4結(jié) 語(yǔ)
本文提出了一種新型GA-RBF神經(jīng)網(wǎng)絡(luò)逆控制方法,用以解決神經(jīng)網(wǎng)絡(luò)逆系統(tǒng)方法在實(shí)際應(yīng)用時(shí)逆模型難以求取等問(wèn)題。該方法兼具遺傳算法和RBF網(wǎng)絡(luò)的雙重優(yōu)點(diǎn)。遺傳算法具有自組織性、自適應(yīng)性和智能性,可以解決一些復(fù)雜的非線性問(wèn)題。RBF網(wǎng)絡(luò)的學(xué)習(xí)速度快,能更好達(dá)到實(shí)時(shí)控制,避免了BP網(wǎng)絡(luò)容易局部極小的問(wèn)題。將兩電機(jī)調(diào)速系統(tǒng)作為控制對(duì)象,進(jìn)行了實(shí)驗(yàn)驗(yàn)證,證明了理論分析的正確性。
[1] Michael C A,Safacas A N.Dynamic and vibration analysis of a multimotor DC drive system with elastic shafts driving a tissue paper machine[J].IEEE Transactions on Industrial Electronics,2007,54(4):2033-2046.
[2] Abjadi N R,Soltani J,Askari J,et al.Nonlinear sliding-mode control of a multi-motor web-winding system without tension sensor[J].IET Control Theory & Applications,2009,3(4):419-427.
[3] Kim J,Park C,Hwang S,et al.Control algorithm for an independent motor-drive vehicle[J].IEEE Transactions on Vehicular Technology,2010,59(7):3213-3222.
[4] Ben M W,Belhadj J,Pietrzak-David M.Sliding mode observer for mono-inverter bi-motors railway traction system[C]//8th International Multi-Conference on Systems,Signals and Devices(SSD).2011:1-6.
[5] Yu D C,Liu F,Lai P Y,et al.Nonlinear dynamic compensation of sensors using inverse-model-based neural network [J].IEEE Transactions on Instrumentation and Measurement,2008,57(10):2364-2376.
[6] 戴先中,劉國(guó)海,張興華.交流傳動(dòng)神經(jīng)網(wǎng)絡(luò)逆控制[M].北京:機(jī)械工業(yè)出版社,2007.
[7] Zhao Xinlong,Tan Yonghong.Modeling hysteresis and its inverse model using neural networks based on expanded input space method[J].IEEE Transactions on Control Systems Technology,2008,16(3):484-490.
[8] 孫玉坤,任元,黃永紅.磁懸浮開(kāi)關(guān)磁阻電機(jī)懸浮力與旋轉(zhuǎn)力的神經(jīng)網(wǎng)絡(luò)逆解耦控制[J].中國(guó)電機(jī)工程學(xué)報(bào),2008,28(9):81-85.
[9] 宣光銀,胡丹,車暢.基于RBF神經(jīng)網(wǎng)絡(luò)的SVPWM研究[J].微特電機(jī),2011(9):45-47.
[10] 夏軒,許偉明.改進(jìn)的粒子算法對(duì)RBF神經(jīng)網(wǎng)絡(luò)的優(yōu)化[J].計(jì)算機(jī)工程與應(yīng)用,2012,48(5):37-40.
[11] 劉金琨.智能控制[M].北京:電子工業(yè)出版社,2005.
[12] 王廣生,黃守道,高劍.改進(jìn)遺傳算法在永磁電動(dòng)機(jī)優(yōu)化設(shè)計(jì)中的應(yīng)用[J].微特電機(jī),2011(7):9-12.
[13] 張明君,張化光.遺傳算法優(yōu)化的RBF神經(jīng)網(wǎng)絡(luò)控制器[J].電機(jī)與控制學(xué)報(bào),2007,11(2):183-187.
[14] Pehlivanoglu Y V,Baysal O.Vibrational genetic algorithm enhanced with fuzzy logic and neural network[J].Aerospace Scienceand Technology,2010,14(1):56-64.
[15] 廖本先,楊宜民,張學(xué)習(xí).自適應(yīng)遺傳算法和RBF網(wǎng)絡(luò)在傳球中的應(yīng)用[J].計(jì)算機(jī)仿真,2010,27(9):169-172.
[16] 趙海波.基于改進(jìn)遺傳RBF神經(jīng)網(wǎng)絡(luò)的雙電機(jī)驅(qū)動(dòng)伺服系統(tǒng)控制[J].井岡山大學(xué)學(xué)報(bào),2011,32(4):76-80.
- 微特電機(jī)的其它文章
- 基于模型預(yù)測(cè)前饋的滾轉(zhuǎn)穩(wěn)定伺服系統(tǒng)控制研究
- 基于dsPIC30F4012的無(wú)刷直流電動(dòng)機(jī)控制系統(tǒng)設(shè)計(jì)
- 飛輪儲(chǔ)能系統(tǒng)用電動(dòng)/發(fā)電機(jī)的研究
- 基于FPGA的步進(jìn)電動(dòng)機(jī)加減速控制器
- 全數(shù)字化步進(jìn)電動(dòng)機(jī)細(xì)分驅(qū)動(dòng)器設(shè)計(jì)
- 不同轉(zhuǎn)子結(jié)構(gòu)無(wú)刷雙饋電機(jī)的電磁和動(dòng)態(tài)特性分析

