基于非線性多項式的自適應重構算法

李金龍，林嘉宇，袁繼兵，鄭林華

(國防科學技術大學電子科學與工程學院，長沙410073)

1 引言

跳頻技術是無線通信系統提高抗干擾能力、多址組網能力和抗截獲能力的一項重要技術，其實現方法是將一個較寬的頻帶分解為若干個細小的頻隙，然后利用偽隨機序列控制發射機，使得發射機在某一特定時間段內發送特定的載波信號。這個用于控制載波頻率跳變的偽隨機序列就稱為跳頻序列，跳頻序列的偽隨機性決定了其難以預測。近年來，隨著非線性預測由理論轉向實際應用的研究，跳頻序列的建模和預測研究成為通信領域的一個研究熱點。理想的預測建立在可靠的建模與重構基礎之上。本文采用Bernstein多項式對跳頻序列進行建模，并結合遞歸最小二乘(RLS，Recursive Least Squares)［1］自適應濾波算法來實現對跳頻序列的重構。理論分析和仿真實驗表明基于Bernstein多項式的自適應算法能夠很好地對一些常見的跳頻序列進行重構，誤差小而且收斂速度快。

2 Bernstein多項式理論

由 Weierstrass逼近定理［2］可知:定義在區間［0，1］上的連續實函數f(x)，對于任意ε＞0，存在區間［0，1］上的多項式 p(x)，對于任意 x∈［0，1］，滿足|f(x)-p(x)|＜ε。即對于任一有界閉區間的連續函數都可以用該區間上的任意多項式以任意精度進行逼近。這意味著可以將連續函數的區間劃分為若干個充分小的區間，從而用低階多項式對連續函數進行任意逼近。

上述提到的多項式有多種，這里采用Bernstein多項式來逼近跳頻序列的動力學系統，Bernstein多項式定義如下:

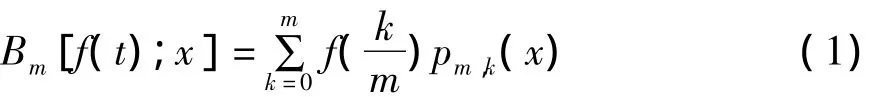
式中

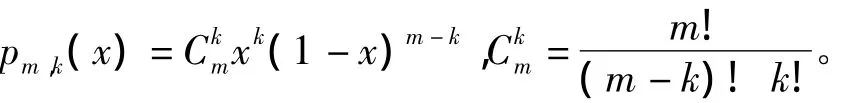
由文獻［2］可得Bernstein多項式與連續函數f(x)在區間［0，1］上一致，即 Bernstein多項式可以對［0，1］區間上的任意連續函數進行逼近。這也是選用Bernstein多項式來對跳頻序列進行建模與重構的原因。

上述定理很容易推廣到多元的情況。考慮到n維方體

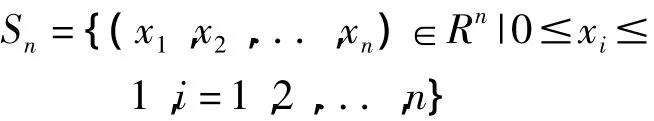
對于給定的 n元實值連續函數 f(x1，x2，...，xn)∈C(Sn)，構造 n 元乘積型Bernstein 多項式［2］:

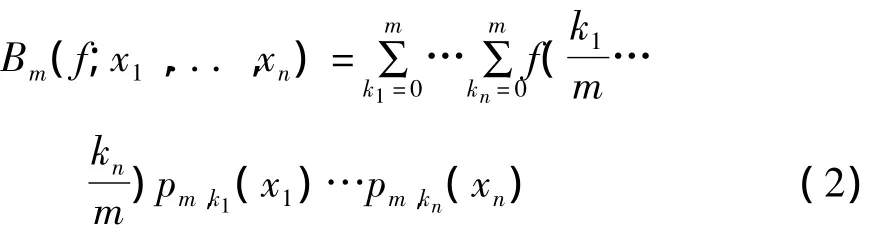
式中

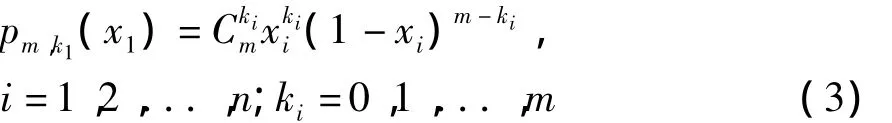
由式(2)可以利用n元m階Bernstein多項式對定義在任意n維方體的連續函數f(x1，x2，...，xn)進行任意精度的逼近。在對跳頻序列進行重構的實際應用中，由于跳頻序列的動力學方程未知，因此可以采用待定參數的Bernstein多項式［3］:

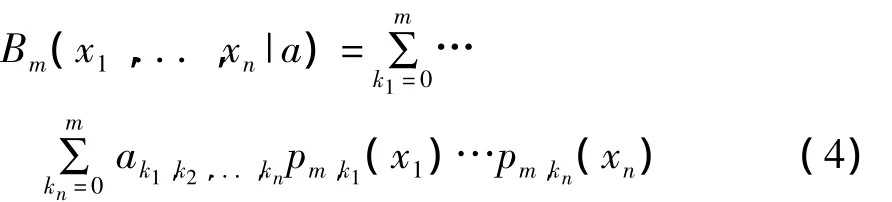
式 中 a =(ak1，k2，...，kn，ki=0，...，m;i=1，2，...，n)為待定參數矢量。

式(4)中的多項式共有(m+1)n個參數，在參數取適當值的情況下可以逼近任意n維方體上的任意n元連續函數，但是參數運算量太大不利于進行實時處理。這里采用將變量的交叉乘積項去除的方法，以達到減少參數個數的目的。

去除交叉項后的n元m階待定參數的Bernstein多項式為:

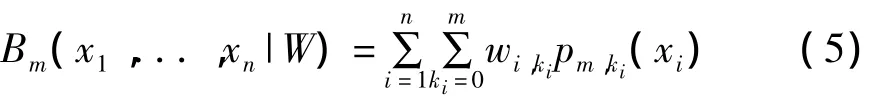
式中 W=(wi，ki，ki=0，...，m;i=1，...，n)為待定參數矢量。

式(5)就是實際建模中采用的Bernstein多項式，將其與式(4)作對比可以看出略去乘積交叉項后參數個數下降為(m+1)·n，大大減少了多項式參數的個數，提高了算法的運算速度。這種做法是以犧牲Bernstein多項式對函數的逼近能力為代價來換取運算速度的提高，但是從后面的重構結果中可以看出，略去乘積交叉項后仍然能夠對跳頻序列進行很好地重構。

3 算法介紹

采用的自適應重構算法是先利用Bernstein多項式對跳頻序列進行建模，然后再利用RLS算法對多項式中的參數進行自適應濾波，從而達到理想的重構結果。為了降低算法復雜度，減小內存開銷，實驗中利用數學特性減少多項式參數的計算量，同時對自適應濾波算法進行改進，在每次訓練中只保留濾波系數的有效矢量，得到一種稀疏的自適應濾波器。

3.1 多項式建模

典型的自適應濾波器結構如圖1所示。其中自適應算法模塊根據實際應用中的性能指標，以及輸入信號和期望響應對濾波器系數的參數進行調整，當找到使自適應濾波器具有最佳性能的濾波器權系數W后調整停止。實驗中采用RLS自適應算法來對濾波器系數W進行調整。而濾波結構模塊則用于對輸入信號x進行度量，形成輸出信號y。如果濾波器的輸出是輸入的線性組合，則稱該濾波器為線性濾波器，否則為非線性濾波器。所謂的建模也就是在濾波結構中確定輸入信號與輸出信號的映射關系，由于實驗中采用Bernstein非線性多項式進行建模，所以該濾波器為非線性濾波器。

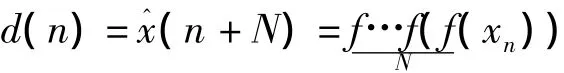
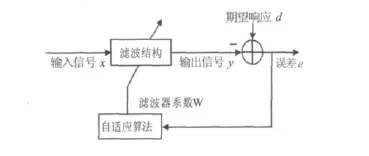
圖1 自適應濾波器的典型結構圖

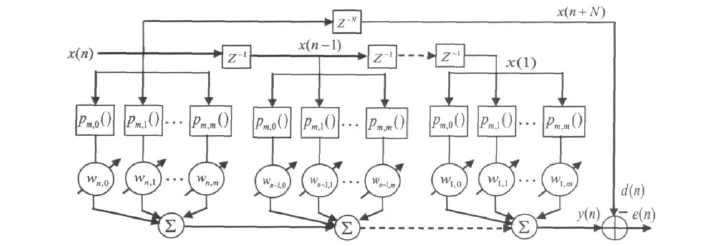
圖2 Bernstein多項式建模后的濾波器橫向結構圖

3.2 自適應重構算法

跳頻序列不服從高斯分布，表現出局部非平穩特性。在局部變化比較劇烈的跳頻序列中要提高重構精度，對算法的收斂速度提出了較高的要求，因此實驗中采用RLS這種快速收斂的的自適應算法與上述的Bernstein建模方法相結合，來實現對跳頻序列的重構。具體算法流程如下［4］:

3.2.1 給定關鍵參數并對迭代變量進行初始化

1)給定每幀輸入的樣點數 n、預測器中Bernstein多項式核函數個數m，以及每幀預測的步數N。

2)給定RLS算法中的兩個重要參量λ和δ。其中，λ是遺忘因子，用于調整權值;δ是一個很小的正整數，用于提高收斂速度，迭代初值P(0)=δ-1I。

3)構造(m+1)·n階濾波器權系數W，并將其值初始化為0。

3.2.2 重構跳頻序列動力學方程獲取濾波器權系數

1)對每幀輸入的樣點利用Bernstein多項式建模后得到濾波器輸入列向量X(k)=［x(k-n+1)x(k-n)...x(k)］T，由Bernstein多項式可知:

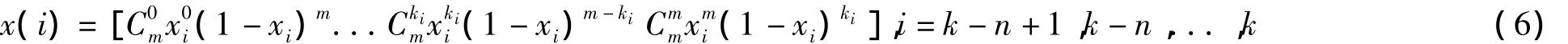
2)利用RLS自適應迭代算法調整濾波器權系數:

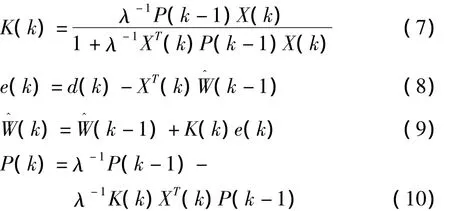
3.3 算法復雜度改進

RLS自適應算法是以加權誤差平方和的代價函數最小為最優化目標，它具有收斂速度快，且其收斂性能與輸入頻譜特性無關，但存在計算復雜度較高的缺陷。實驗中分別從數學特性和算法的角度出發來降低復雜度。

3.3.1 基于數學特性降低復雜度

通過觀察分析可以看到整個算法中，式(3)的計算量相當大。進行一次迭代運算需要的計算量為(由于加減運算較簡單，在這里不考慮):(m+1)·n次組合運算;2(m+1)·n次指數運算;2(m+1)·n次乘法運算。而指數運算以及組合運算的運算量又較乘法的運算大，因此主要考慮降低指數運算和組合運算的運算量。

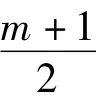
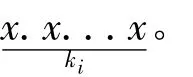
在計算過程中就可以利用上一次的運算結果xki-1乘以x得到xki，減少了計算量，使算法復雜度得到了降低，在m取值較大時效果更為明顯。利用數學特性降低算法復雜度后，計算量的變化如表1所示，從表中可以看出改進后乘法運算量增加(m-1)·n，但是組合函數運算量和指數運算量卻在很大程度上得到了降低。

本文采用差減法計算螢石中氟化鈣含量。全鈣的測定采用EDTA滴定法。關于碳酸鈣的測定，本文在參考標準GB/T 5195.1—2006方法1、經驗修正法和去碳酸鈣的螢石樣作空白校正法[8]的基礎上，提出了一種新的方法。即分別稱取兩份不同質量的螢石試樣，用稀鹽酸浸取其中的碳酸鈣，然后控制實驗條件(溶液pH值、鈣離子濃度、體積)，使兩份溶液中氟化鈣溶解量趨于一致，對兩份溶液進行干過濾，采用EDTA滴定法測定兩份溶液中全鈣的質量差(以碳酸鈣計)，經過換算可得試樣中碳酸鈣的含量。最終，實現了差減法對螢石中氟化鈣的測定。

表1 復雜度降低前后計算量對照表

3.3.2 基于稀疏自適應濾波算法降低復雜度

在程序調試中發現濾波器系數矢量W中，有一部分分量非常接近0。這些分量對于實際重構結果的貢獻為“0”，這里將這些接近0的分量稱為無效分量，而其他分量為有效分量，則相應的輸入信號矢量X也由無效分量和有效分量構成。因此，實驗在文獻［3］的基礎上提出了一種稀疏多項式自適應重構算法。該濾波器采用非線性自適應迭代算法進行訓練，每次訓練只保留濾波器權系數和輸入信號X的有效分量用于跳頻序列的重構，從而實現濾波器權系數的減小。

假設某次訓練結束后，濾波器權系數矢量W(k)為:

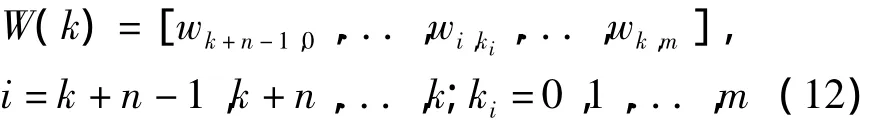
逐一考察 W(k)的各分量 wi，ki，當滿足條件|wi，ki＜ α 時，則認為 wi，ki與相對應的輸入信號的分量為無效分量，否則為有效分量。其中，門限α為非常小的數，實驗中根據經驗設定其取值范圍為α∈(0，3×10-5］。訓練結束后，只保留有效分量對跳頻序列進行重構。這樣不僅使非線性多項式自適應濾波器的規模減小，提高算法的收斂速度，使算法復雜度降低，同時在硬件實現上也減小了內存的開銷。在輸入樣點數n和Bernstein多項式核函數個數m較大的情況下，這種稀疏算法的效果更加明顯。

4 仿真實驗

由于Bernstein多項式中輸入信號取值范圍為［0，1］，因此在仿真實驗前先按照(13)式對跳頻序列進行歸一化處理:

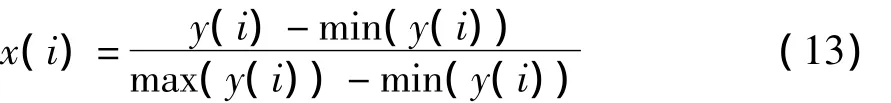
式中，{y(i)}為原始跳頻序列，{x(i)}為歸一化后的跳頻序列。

4.1 重構性能指標及仿真參數確定

在仿真實驗中取歸一化后的跳頻序列{x(i)}來進行建模重構。假定待重構的原始數據為x(k)，對應的重構數據為x^(k)，重構數據的長度為L。仿真實驗中使用均方誤差(Pmse)、相對誤差(Prmse)和重構準確率(Pnice)作為評測標準。其中，均方誤差的計算式為:

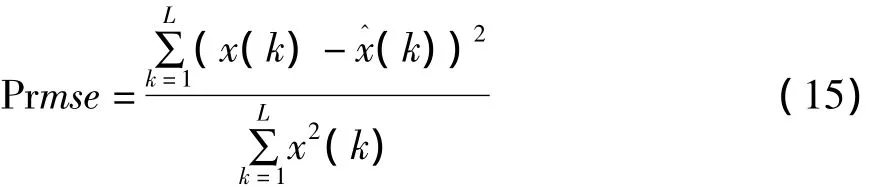
由于跳頻序列{x(i)}的取值區間為［0，1］，所以當x(k)-0.025≤x^(k)≤x(k)+0.025時就可以認為是準確重構，該段范圍占［0，1］區間的5%。將準確重構的跳頻碼數除以總碼數就可以得到重構準確率。

重構算法中所涉及的參數包括輸入樣點數n、Bernstein多項式核函數個數m、重構數據的長度為L、門限值α以及RLS迭代算法中的初始化參數δ和λ。對不同跳頻序列的重構性能而言，后面四個參數的影響很小可以忽略不計。因此，在仿真實驗中可根據經驗值直接設定其取值分別為:L=1000，α=0，δ=10-4;λ=0.995。而對于參數n和m，由于不同的跳頻序列有不同的非線性映射關系，因此采用逐步試探法來對不同的跳頻序列確定合適的n和m。實驗中先分別令n和m的值等于1，然后逐步增加其權值，觀察在不同取值情況下的重構性能。通過實驗發現對不同的跳頻序列，在n和m取值較小的情況下都能對其進行很好的重構，隨著n和m值的增加其重構性能變化不大，呈現微小的上升趨勢。為了方便計算分析，實驗中對于所有的跳頻序列我們均取n=2，m=6。

4.2 實驗中使用的跳頻序列

為了驗證算法對跳頻序列的重構性能，實驗中對一些常見的跳頻序列分別進行重構。使用的跳頻序列如下:

1)藍牙79跳跳頻序列

根據文獻［5］的算法產生藍牙79跳跳頻序列。其中藍牙設備地址低32位值ULA為:0xd5ebc7a6，而主設備時鐘CLK的初值為:0x00000000。

2)Lozi映射產生的跳頻序列

Lozi映射的關系式如式(16)所示，取x分量作為跳頻序列。

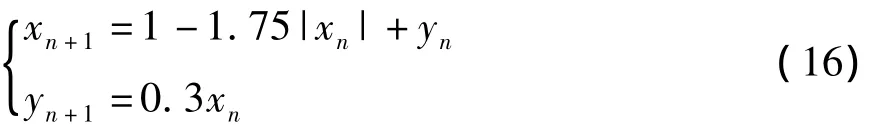
式中，x0=0.2，y0=0。

3)Lorenz流產生的跳頻序列

Lorenz流的關系式如式(17)所示，取x分量作為跳頻序列。

式中，σ =10，r=34，b=8/3。

4)Rossler流產生的跳頻序列

Rossler流的關系式如式(18)所示，取x分量作為跳頻序列。

式中 d=0.15，e=0.2，f=10。

以上四個跳頻序列中，藍牙跳頻序列和Lozi跳頻序列為離散序列，而Lorenz跳頻序列和Rossler跳頻序列為連續序列。仿真實驗中，對于所有跳頻序列，每次實驗均產生1002個真實值，并對后1000個實值進行重構，分析算法的重構性能。

4.3 仿真實驗結果

下面根據4.1節中參數的取值以及重構性能指標，對4.2節中的跳頻序列進行分析，分析過程中采用3.1節提到的直接多步重構方法。首先選取藍牙跳頻序列分析重構步數對序列重構性能的影響。

從表2的實驗數據中可以看出，不同重構步數對跳頻序列的重構性能影響不大，本文的自適應重構算法在不同重構步數下都能夠對跳頻序列進行很好的重構。因此，下面只取一步重構對不同的跳頻序列進行重構性能分析。

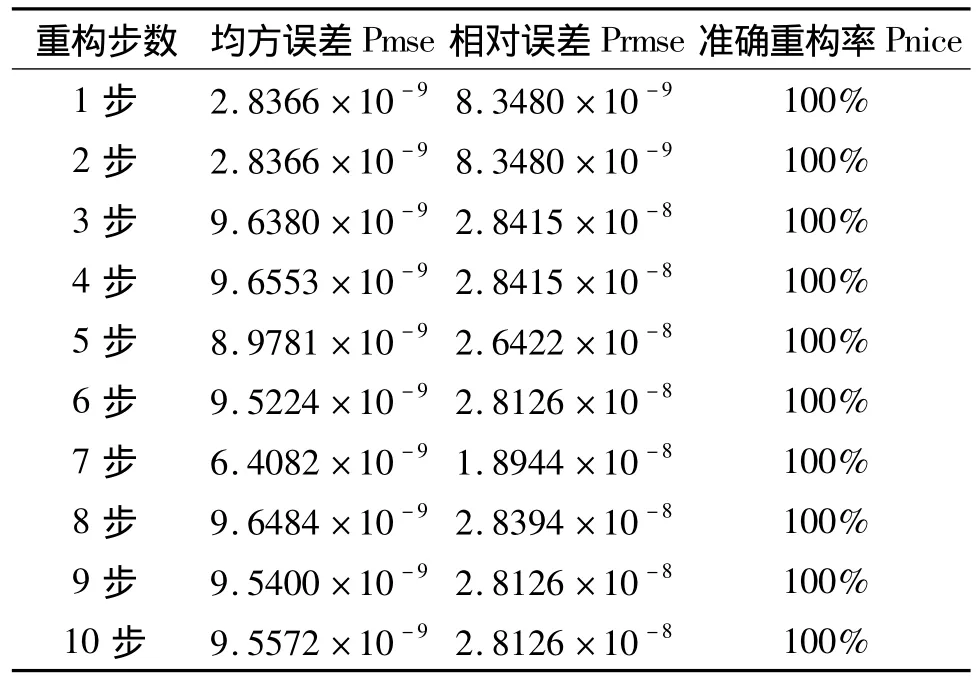
表2 藍牙跳頻序列的直接多步重構性能

從表3可以看出，自適應重構算法對4.2節提到的4個常見的跳頻序列都有很好的重構效果和重構精度。圖3-圖6分別畫出四個跳頻序列一步重構圖和相應的誤差性能仿真曲線，每次取1000個點進行仿真。為了便于實驗觀測，在重構圖中每隔5個點輸出1個點標示。

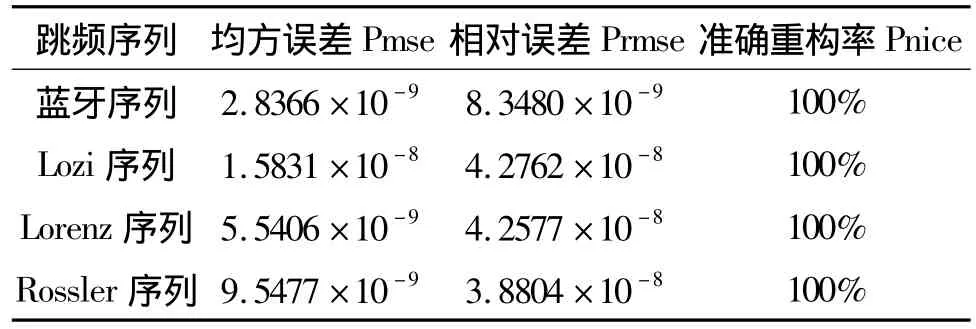
表3 不同跳頻序列的一步重構性能

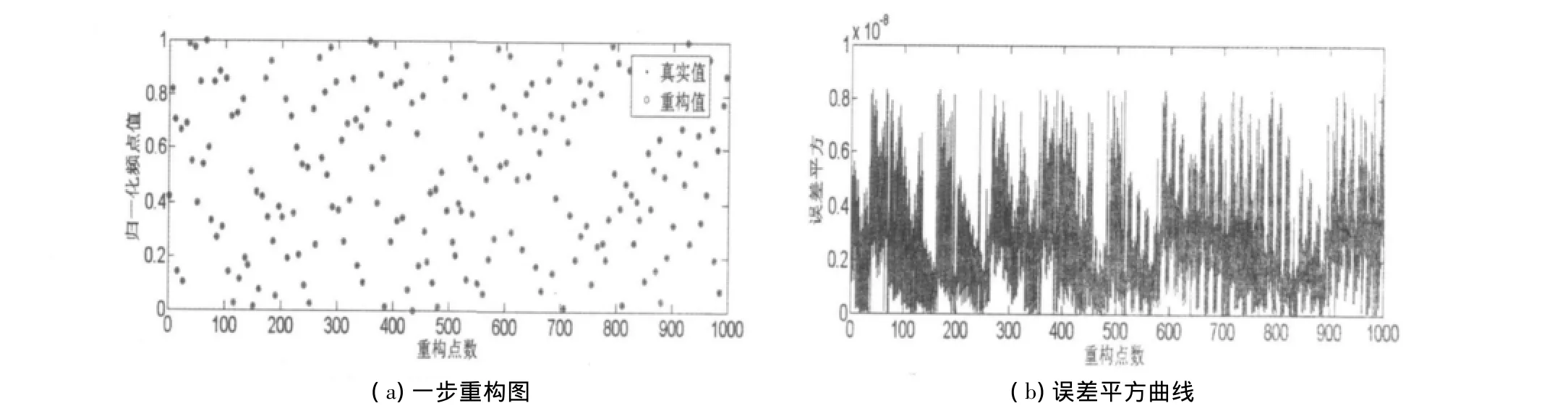
圖3 藍牙跳頻序列一步重構仿真圖

圖4 Lozi跳頻序列一步重構仿真圖

圖5 Lorenz跳頻序列一步重構仿真圖

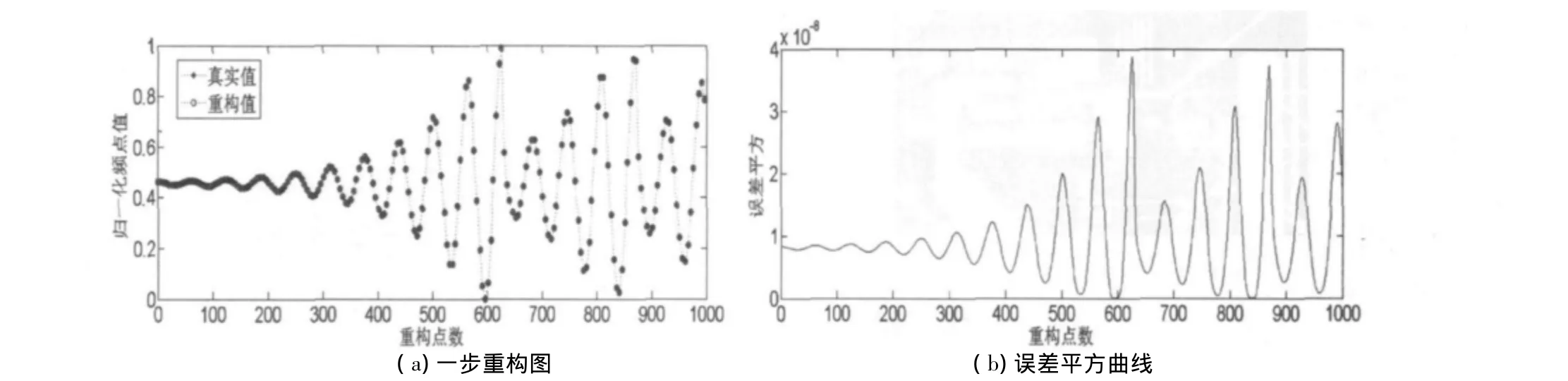
圖6 Rossler跳頻序列一步重構仿真圖

從上述仿真實驗的重構圖中可以看出本文的自適應重構算法，對離散跳頻序列和連續跳頻序列均能夠實現很好的重構。從誤差平方曲線可以看出，RLS算法的收斂性強，誤差平方在數量級為10-8范圍內波動。同時，從連續跳頻序列的重構圖和誤差平方曲線中還可以較為直觀地看出誤差平方曲線與跳頻序列在形狀上極為相似。

下面選取藍牙跳頻序列的一步重構來分析3.3節中稀疏算法對重構性能的影響。其濾波器系數圖如圖7所示，從圖中可以看出濾波器權系數的值有一部分分布在0附近，因此可以采用稀疏算法來降低算法復雜度。表4給出了不同門限值下的藍牙跳頻序列的一步重構性能。

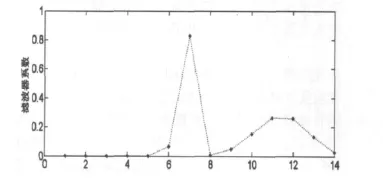
圖7 藍牙跳頻序列一步重構濾波器系數圖

表4 不同門限值下藍牙序列的一步重構性能

從表中可以看出α的取值越大，重構濾波器的濾波系數越少，算法越簡單，反之，濾波器系數越多，算法越復雜。實際使用中，必須在非零wi，ki數與重構精度之間進行折衷考慮，設計合理的門限值。即在不損失重構精度的前提下，盡可能地降低算法的復雜度。

5 結束語

針對跳頻序列重構問題，本文研究實現了一種基于Bernstein非線性多項式的自適應重構算法，并對算法的復雜度進行改進。在算法改進中，利用Bernstein多項式參數的數學特性以及濾波器系數稀疏的特點來降低算法的復雜度。通過對藍牙跳頻序列、Lozi跳頻序列、Lorenz跳頻序列和Rossler跳頻序列的重構仿真實驗可以看出，本文的算法能夠對一般的跳頻序列進行有效的重構。下一步工作主要針對本文算法在高重構精度的條件下，如何實現對跳頻序列進行高精度預測的研究。

［1］ S.Haykin.Adaptive Filter Theory，4th edition［M］.Upper Saddle River，New Jersey:Prentice Hall，2002.

［2］ 梁學章，李強.多元逼近［M］.北京:國防工業出版社，2005.

［3］ 涂靖.跳頻碼序列建模與預測研究［D］.成都:電子科技大學，2008.

［4］ 皇甫堪，陳建文，樓生強.現代數字信號處理［M］.北京:電子工業出版社，2004.

［5］ 曲剛，許宗澤，趙莉娟.Bluetooth跳頻算法及其性能分析［J］.南京航空航天大學學報，2001，33(6):574-578.

［6］ 張家樹，肖先賜.用于混沌時間序列自適應預測的一種少參數二階Volterra濾波器［J］.物理學報，2001，50(7):1248-1254.

［7］ Weisstein E W.Weierstrass approximation theorem［EB/OL］.［2009-10-27］.http://mathworld.wolfram.com/Weierstrass Approximation Theorem.html.

［8］ Hongbin Du，Huihe Shao and Pingjing Yao.Adaptive Neural Network Control for a Classof Low-Triangular-Structured Nonlinear Systems［J］.IEEE Transactions on Neural Networks，2006，17(2):509-514.