非理想信道信息下雙向多中繼選擇系統(tǒng)性能分析
史寅科 邱 玲
(中國科學(xué)技術(shù)大學(xué)個人通信與擴頻實驗室 合肥 230027)
1 引言
中繼協(xié)作技術(shù)能有效提高用戶吞吐量,擴展無線通信系統(tǒng)的覆蓋范圍[1-4]。在傳統(tǒng)的半雙工中繼系統(tǒng)中,雙向中繼技術(shù)由于只需要兩個或3個時隙就能完成信息的交互而受到廣泛關(guān)注。文獻[1]和文獻[2]分別給出了采用三時隙放大轉(zhuǎn)發(fā)(AF)-時分廣播(Time Division BroadCast, TDBC)協(xié)議的雙向中繼選擇系統(tǒng)以及多用戶雙向中繼系統(tǒng)的中斷概率;文獻[3]給出了采用二時隙放大轉(zhuǎn)發(fā)-多址廣播(Multiple Access BroadCast, MABC)協(xié)議的雙向多中繼系統(tǒng)的中斷概率、符號差錯率以及容量界。上述文獻分析的都是系統(tǒng)能獲得的理論容量界或是在理論容量界下系統(tǒng)的中斷概率。為了分析實際系統(tǒng)可達的頻譜效率,文獻[4]將自適應(yīng)調(diào)制技術(shù)應(yīng)用于基于MABC協(xié)議的雙向多中繼系統(tǒng)中,給出了單中繼以及中繼選擇方式下系統(tǒng)的平均頻譜效率(Average Spectrum Efficiency, ASE)以及平均比特差錯率(Average Bit Error Rate, ABER)的閉式表達式。但目前還沒有文獻分析采用自適應(yīng)調(diào)制的基于TDBC協(xié)議的雙向多中繼選擇系統(tǒng)的平均頻譜效率、中斷概率。對于MABC協(xié)議,中繼直接對從用戶接收到的信號進行放大后轉(zhuǎn)發(fā),不需要考慮中繼端的功率分配問題,但對于TDBC協(xié)議,中繼需要對前兩時隙接收到的用戶信號進行疊加后轉(zhuǎn)發(fā),這就涉及到本文需要解決的另一個問題:中繼端如何進行功率分配。
無論是兩時隙還是三時隙雙向中繼傳輸,源端都需要對接收信號進行自干擾消除才能得到對方的信號,但在實際通信系統(tǒng)中,由于信道估計誤差的存在,自干擾無法完全消除,這將嚴重影響系統(tǒng)性能,因此研究非理想信道信息下雙向中繼傳輸系統(tǒng)的性能對實際系統(tǒng)的設(shè)計具有更重要的意義。本文主要給出了存在信道估計誤差時,基于TDBC協(xié)議的雙向多中繼選擇系統(tǒng)的端到端信干噪比表達式,并通過不等式縮放的方式將表達式轉(zhuǎn)化為多個指數(shù)分布變量和的形式,求出了其累積概率密度函數(shù)(CDF)以及概率密度函數(shù)(PDF),并利用該分布推導(dǎo)了自適應(yīng)調(diào)制方式下系統(tǒng)的平均頻譜效率的上界。為了降低信道估計誤差對系統(tǒng)性能的影響,本文進一步提出了一種在最大化系統(tǒng)平均頻譜效率下中繼端最優(yōu)的功率分配(Power Allocation, PA)策略。
2 系統(tǒng)模型
考慮如圖1所示的雙向多中繼系統(tǒng),用戶U1通過m個工作在半雙工模式的放大轉(zhuǎn)發(fā)中繼節(jié)點(R1, … ,Ri, … ,Rm)與用戶U2交互信息。假設(shè)系統(tǒng)工作在時分雙工(TDD)模式下,用戶與中繼具有相同的發(fā)送功率E。用戶與用戶、用戶與中繼Ri間的信道經(jīng)歷的小尺度衰落為瑞利衰落,同時還經(jīng)歷大尺度衰落。假設(shè)信道變化是緩慢的,在一次中繼傳輸過程中信道保持不變。U1與U2,U1與中繼Ri,U2與中繼Ri之間的信道分別記為f~CN( 0,),hi~CN(0,),gi~CN( 0,),它們之間存在如下關(guān)系:其中d0為兩用戶間的距離,為用戶U1與中繼Ri的距離,為用戶U2與中繼Ri的距離,δ為路徑損耗因子,X~CN( 0,σ2)表示X服從均值為0,方差為σ2的復(fù)高斯分布。
傳輸過程被分為3個時隙,在時隙1,U2與中繼處于靜默狀態(tài),用戶U1廣播調(diào)制信號x1給用戶U2以及中繼,U2以及中繼Ri接收到的信號分別為
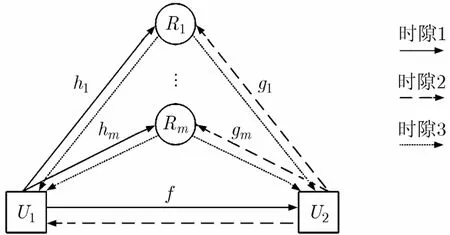
圖1 三時隙雙向多中繼系統(tǒng)傳輸模型
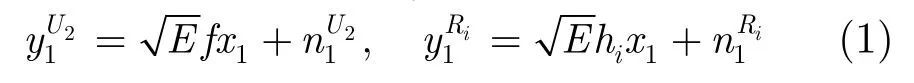
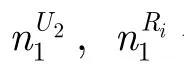

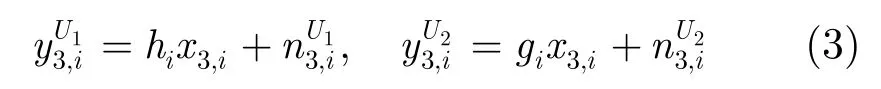
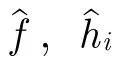
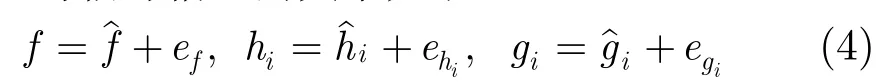
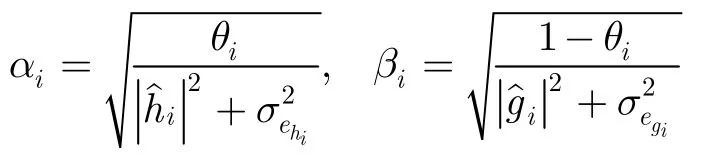
θi為中繼Ri的功率分配因子。
利用TDD系統(tǒng)信道的互易性,U1和U2能獲取中繼Ri與各自鏈路之間的估計信道。U1,U2各自將時隙3接收到的中繼Ri的信號進行自干擾消除,得到它們的方差分別為
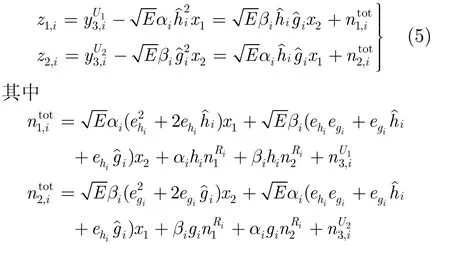
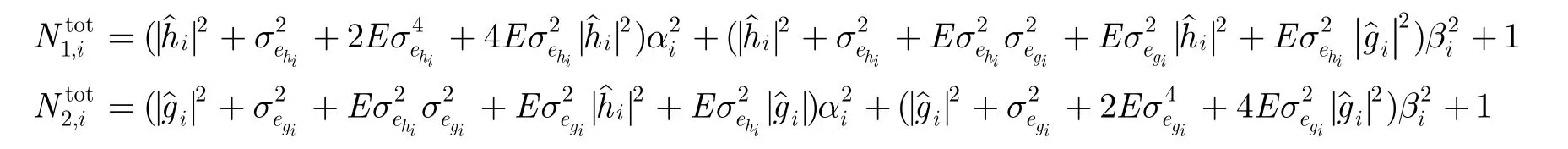
則U1,U2從中繼Ri接收到的信號經(jīng)過自干擾消除后的信干噪比分別為

假設(shè)用戶選擇中繼進行協(xié)作(中繼選擇策略見3.1節(jié)),U1,U2利用最大比合并方式合并從對方以及從中繼接收到的經(jīng)過自干擾消除后的信號,則兩個用戶得到的合并信號分別為
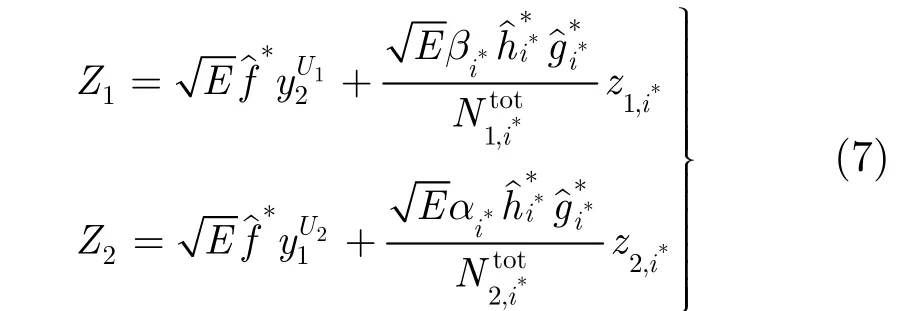
令k∈ { 1,2},根據(jù)式(7)我們可以得到用戶Uk的端到端信干噪比為

3 雙向多中繼選擇系統(tǒng)性能分析
本節(jié)首先給出基于最大化和容量的中繼選擇策略,然后分析用戶端到端信干噪比的分布,最后給出采用自適應(yīng)M階正交幅度調(diào)制(M- QAM )的雙向多中繼選擇系統(tǒng)的 ASE以及中繼端最優(yōu)的功率分配策略。
3.1 中繼選擇策略
如果選擇中繼Ri進行協(xié)作傳輸,則根據(jù)式(8)給出的端到端信干噪比,可以得出在高發(fā)送信噪比下系統(tǒng)近似的香農(nóng)和容量為

我們采用最大化和容量的中繼選擇策略,即

文獻[4]通過仿真證明這種中繼選擇策略性能接近最優(yōu)的中繼選擇策略。
3.2 端到端信干噪比分布
本節(jié)主要分析用戶U1的端到端信干噪比的CDF以及PDF,用戶U2的端到端信干噪比的CDF以及PDF可以利用同樣的方法得到。
首先分析U1接收到的中繼Ri的信號經(jīng)過自干擾消除后信干噪比分布。從式(6)可以看出它的表達式比較復(fù)雜,要求出其確切分布非常困難。幸運的是,通過不等式縮放的方式能得出Γ1,i上界的分布。推導(dǎo)過程如下:

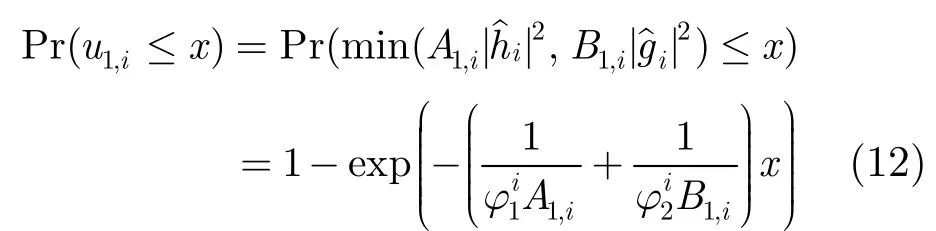
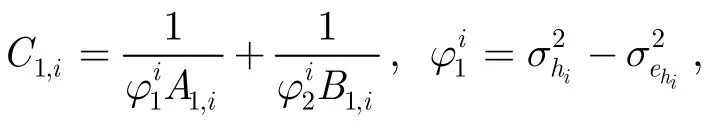
U2,Γ2,i的上界服從參數(shù)為C2,i的指數(shù)分布,其中
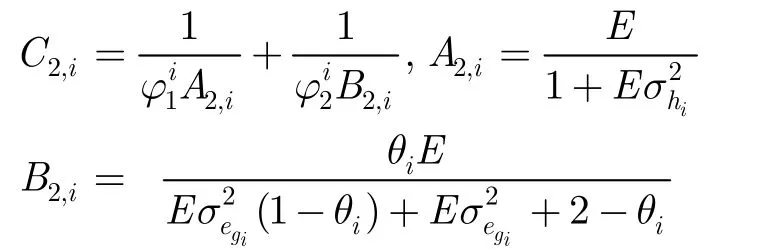
從上面通過不等式的縮放變換本節(jié)得出了Γ1,i,Γ2,i上界是服從指數(shù)分布的隨機變量,這個有意思的結(jié)論大大簡化了后面對系統(tǒng)性能的分析。
根據(jù)3.1節(jié)的中繼選擇策略,不難得出


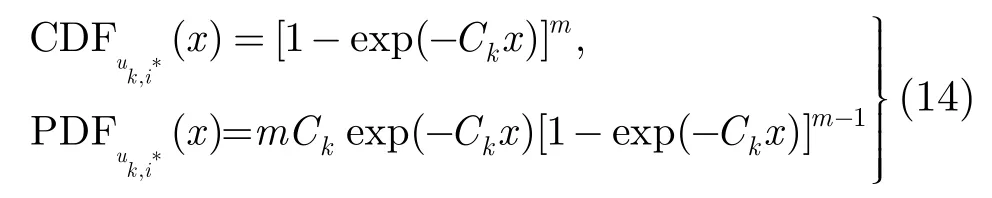



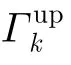
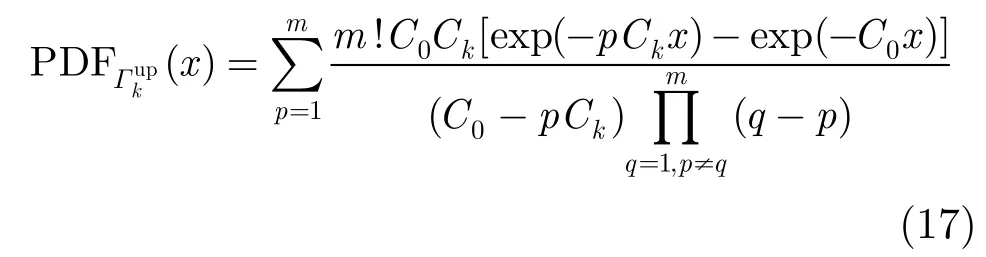
對式(17)積分可得CDF為
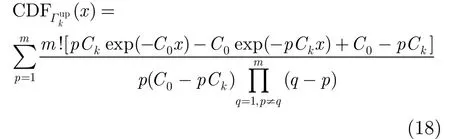
3.3 采用自適應(yīng)調(diào)制的雙向多中繼系統(tǒng)容量
自適應(yīng)調(diào)制能根據(jù)信道變化情況,自適應(yīng)地改變發(fā)送信號的調(diào)制方式,從而提高系統(tǒng)容量。假定用戶U1和用戶U2業(yè)務(wù)需求的誤碼率要小于,并且考慮利用M- QAM 調(diào)制方式,根據(jù)文獻[6],在AWGN信道下采用格雷映射的相干M- QAM 調(diào)制的近似誤碼率可以近似為
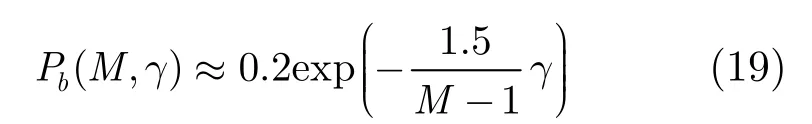
其中γ為接收信噪比,根據(jù)式(19)可以得出連續(xù)速率自適應(yīng)(ACR)調(diào)制[7]的瞬時頻譜效率為
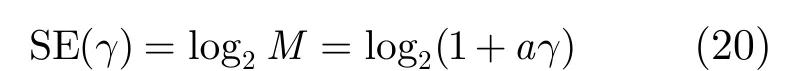
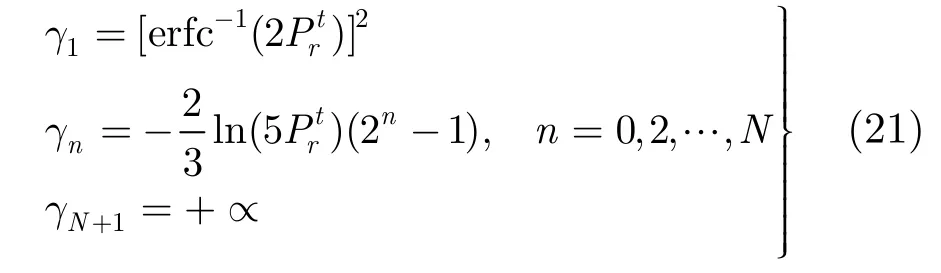
上述臨界點指:當(dāng)接收到的有效信干噪比小于γ1時不發(fā)送任何數(shù)據(jù),當(dāng)大于γN+1時采用2N- Q AM 調(diào)制,在γ1與γN+1之間時采用2n-QAM (1≤n≤N- 1 )。
兩用戶各自根據(jù)信道狀況分別采用ADR調(diào)制,如果有一方端到端信干噪比小于或等于γ1,則雙方均不發(fā)送數(shù)據(jù),根據(jù)以上分析我們可以得出在非理想信道信息下雙向多中繼選擇系統(tǒng)的平均頻譜效率的上界為
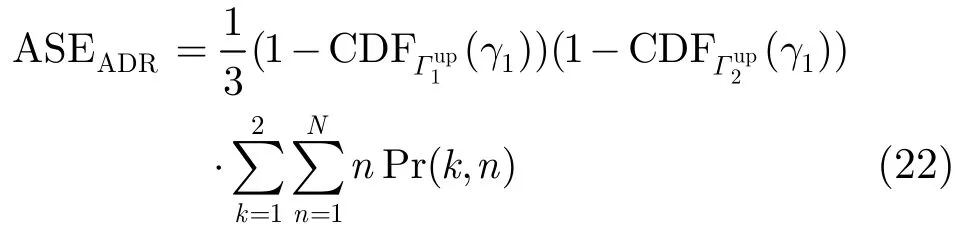
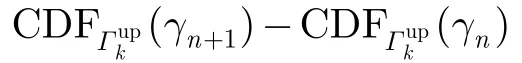

3.4 功率分配
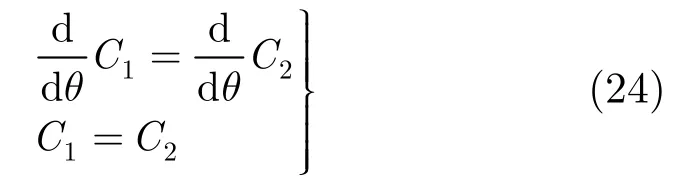
這一節(jié)給出一種最大化系統(tǒng)平均頻譜效率的中繼端最優(yōu)功率分配策略。根據(jù) 3.3節(jié)給出的平均頻譜效率的表達式,不難看出它是個關(guān)于θ的凸函數(shù),因此中繼端最優(yōu)功率分配問題可以建模為如下凸優(yōu)化問題:

解式(23)的凸優(yōu)化問題,可以得到
4 仿真分析

圖2給出了d1/d0= 0 .1時,中繼端等功率分配以及最優(yōu)功率分配條件下平均頻譜效率隨發(fā)送信噪比(SNR)以及信道估計誤差變化曲線。從圖中可以看出,理論分析的平均頻譜效率上界表達式與蒙特卡洛(MC)仿真結(jié)果相吻合。當(dāng)不存在信道估計誤差時,系統(tǒng)性能最好,當(dāng)存在信道估計誤差時,信道估計誤差越大,系統(tǒng)性能越差,還會出現(xiàn)平臺,這是由于自干擾不能完全被消除使得系統(tǒng)變成一個干擾受限的系統(tǒng),在發(fā)送信噪比比較大的時候,端到端信干噪比趨近于一個常數(shù)(這個常數(shù)受信道估計誤差、中繼數(shù)目以及功率分配因子的影響),導(dǎo)致系統(tǒng)的容量也受限。從圖中還可以看出,本文提出的中繼端最優(yōu)功率分配策略要好于平均功率分配策略,這從一定程度上克服了信道估計誤差對系統(tǒng)性能的影響。
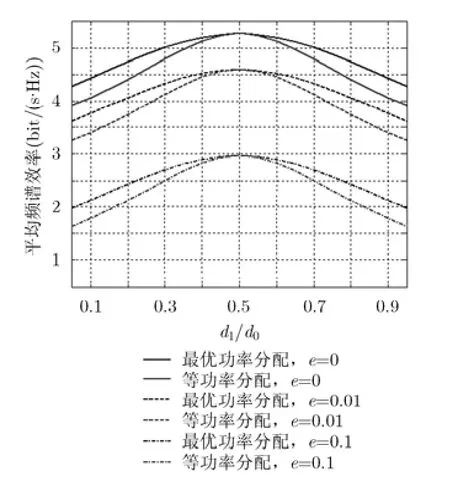
圖3給出了中繼端等功率分配以及最優(yōu)功率分配條件下,理論分析得出的平均頻譜效率隨d1/d0變化的曲線。固定發(fā)送信噪比為 20 dB,從圖中可以看出,無論是否存在信道估計誤差,都有如下結(jié)論:當(dāng)中繼越靠近用戶時,本文提出的最優(yōu)功率分配方式相對于等功率分配方式就越好。這很好理解,比如當(dāng)中繼靠近用戶U1時,中繼在時隙1接收到的來自用戶U1的信號比較強,在時隙2接收到的來自用戶U2的信號相對較弱,如果在第3個時隙中繼將更多的能量分配給時隙1接收到的信號,根據(jù)功率注水的思想,系統(tǒng)性能就會越好。
5 結(jié)束語
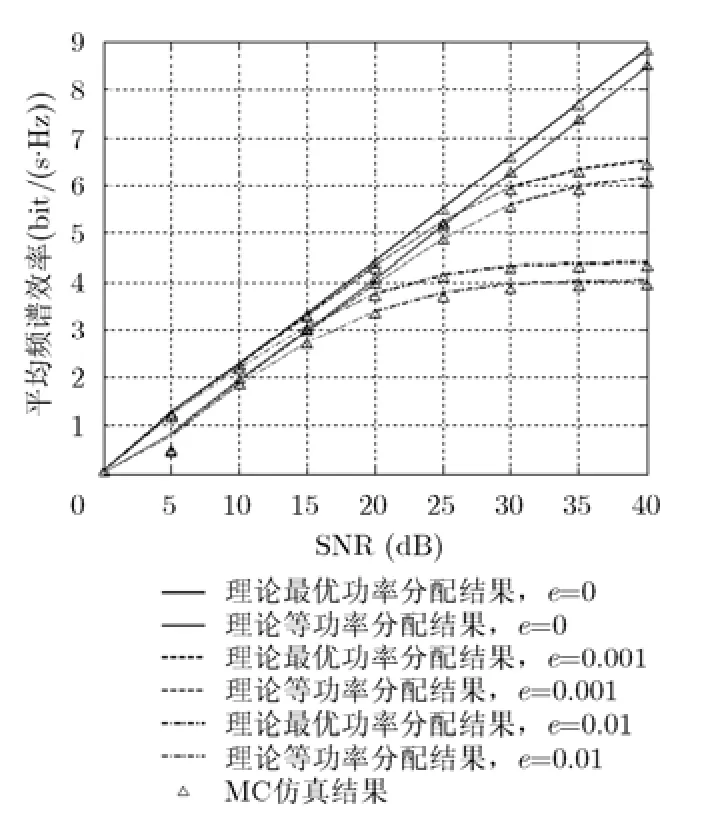
圖2 中繼端等功率以及最優(yōu)功率分配下平均頻譜效率隨發(fā)送信噪比及信道估計誤差變化曲線
本文分析了存在信道估計誤差時,采用自適應(yīng)調(diào)制的基于三時隙時分廣播協(xié)議的雙向多中繼選擇系統(tǒng)的性能,中繼采用放大轉(zhuǎn)發(fā)方式,給出了系統(tǒng)的端到端信干噪比表達式,并通過不等式縮放將表達式轉(zhuǎn)化為多個指數(shù)分布變量和的形式,求出了其累積概率密度函數(shù)以及概率密度函數(shù),然后利用端到端信干噪比的分布推導(dǎo)了離散速率自適應(yīng)調(diào)制下系統(tǒng)平均頻譜效率上界的閉式表達式。仿真結(jié)果說明本文給出的平均頻譜效率上界的閉式表達式是系統(tǒng)真實性能的一個很好的近似。為了克服信道估計誤差對系統(tǒng)性能的影響,本文提出了一種中繼端最優(yōu)的功率分配策略,該策略與等功率分配策略相比,當(dāng)中繼越接近于用戶時,采用本文提出的功率分配策略帶來的系統(tǒng)性能提升就越大。
[1]Ju M C and Kim Il-Min. Relay selection with ANC and TDBC protocols in bidirectional relay networks [J].IEEE Transactions on Communications, 2010, 58(12): 3500-3511.
[2]Ding H, Ge J, Costa B,et al.. Two birds with one stone:exploiting direct links for multiuser two-way relaying systems[J].IEEE Transactions on Wireless Communications, 2012,11(1): 54-59.
[3]Hwang K, Ko Y, and Alouini M S. Performance bounds for two-way amplify-and-forward relaying based on relay path selection [C]. Proc. IEEE Vehicular Technology Conference,Barcelona, Spain, Spring, 2009: 1-5.
[4]Hwang K, Ko Y, and Alouini M S. Performance analysis of two-way amplify and forward relaying with adaptive modulation over multiple relay network[J].IEEE Transactions on Communications, 2011, 59(2): 402-406.
[5]Kim N and Hyuncheol P. Performance analysis of MIMO system with linear MMSE receiver [J].IEEE Transactions onWireless Communications, 2008, 7(11): 4474-4478.
[6]Goldsmith A J and Chua Soon-ghee. Variable-rate variablepower MQAM for fading channels[J].IEEE Transactions on Communications, 1997, 45(10): 1218-1230.
[7]Nechiporenko T, Phan K T, Tellambura C,et al..Performance analysis of adaptive M-QAM for rayleigh fading cooperative systems[C]. Proc. IEEE International Conference on Communications, Beijing, China, May 2008: 3393-3399.
[8]Alouini M S and Goldsmith A J. Adaptive modulation over nakagami fading channels[J].WirelessPersonal Communications, 2000, 13(1): 119-143.
[9]Yi Z, Ju M, and Kim Il-Min. Outage probability and optimum combining for time division broadcast protocol[J].IEEE Transactions on Wireless Communications, 2011, 10(5):1362-1367.
[10]Yi Z, Ju M, and Kim Il-Min. Outage probability and optimum power allocation for analog network coding[J].IEEE Transactions on Wireless Communications, 2011, 10(2):407-412.
[11]Seddik K G, Sadek A K, Su W,et al.. Outage analysis and optimal power allocation for multinode relay networks [J].IEEE Signal Processing Letters, 2007, 14(6): 377-380.

