非對稱協作分集通信中網絡編碼的應用

池新生 鄭寶玉 姚 剛 陳建白

①(南京郵電大學信號處理與傳輸研究院 南京 210003)

②(寬帶無線通信與傳感網技術教育部重點實驗室 南京 210003)

1 引言

在具有廣播特性的無線通信傳輸網絡中，每個目的節點能接收到附近各節點發送的幾個信息的副本，這樣很容易產生信息之間的干擾，影響通信性能。為了消除這種干擾，人們把文獻[1]中有線網絡的網絡編碼引入到無線通信系統中。在通信系統的中繼節點對接收到的多個信息進行整合得到源節點信息之間的編碼關系，然后進行信號再生過程。目的節點利用這種編碼關系和本地已知信息就可得到源信息。

在點對點的通信系統中，通信節點之間進行信息的交互，為了增加通信可靠性，往往增加一個中繼節點來轉發源節點發送的信息，構成一個三點協作分集(cooperative diversity)系統，也稱為存在直接鏈路的雙向中繼信道。在協作分集通信系統中，如何實現網絡編碼和協作分集更有效率地結合是當前研究的熱點之一。文獻[2,3]提出了將網絡編碼和協作通信結合的方案，所提方案中兩個移動臺通過互相協作，在多用戶環境中通過共享其他移動用戶的天線，產生多根虛擬發射天線，進而得到相應的分集增益。文獻[4]在多用戶協作中運用廣義動態網絡編碼，目的是在不減少系統吞吐的情況下，增加分集階數。文獻[5]提出了網絡編碼面臨的挑戰，指出網絡編碼的應用不一定都是有利的。同時給出了網絡編碼噪聲(network coding noise)的概念，通過對編碼噪聲的分析，為更有效率地利用網絡編碼指出了方向。隨后人們開始研究非對稱速率傳輸的實現。文獻[6]介紹了存在直接鏈路的雙向中繼信道采取非對稱速率傳輸時在中繼節點進行網絡編碼的 3種方式，以及在源節點的譯碼過程。文獻[7]提出了雙向中繼信道中，中繼節點在廣播階段對非對稱速率信息進行網絡編碼的方式。信道編碼方式的選擇對網絡編碼的實現具有很大的影響。文獻[8]構造的重復累計(Repeat Accumulate, RA)碼在編碼時對信息位進行重復，引入了冗余度，這樣在譯碼時可通過增加的碼字信息進行更好的譯碼。文獻[9]中，在不同用戶之間用重復累計碼進行協作編碼，實現了虛擬分集技術。

以上研究都假設通信系統所處的環境穩定，通信鏈路傳輸能力相同。在點對點的通信系統中，無線通信空間是開放的，通信節點所處的通信環境有差異，通信節點之間鏈路的傳輸能力也不一致。在有差異鏈路的傳輸系統中，為了照顧較差鏈路，保證其傳輸的可靠性，較優鏈路必須以較差鏈路為準則降低其傳輸速率(即采用對稱速率傳輸)。這樣較優鏈路并沒有發揮其最大傳輸能力，從而造成系統的資源浪費。如何利用網絡編碼和非對稱速率傳輸方式來協調這種差異以保證傳輸可靠性和系統的利用效率，將是本文研究的重點。本文提出的基于重復累計(RA)編碼的非對稱速率協同分集網絡編碼方案，在中繼節點通過引入已知信息，實現了非對稱速率信息的網絡編碼，也保證了較差鏈路傳輸可靠性和較優鏈路傳輸的高效率。同時，在源節點采用了對多個信息副本進行聯合譯碼的改進算法，實現了分集增益。

論文的余下內容安排如下：第2節介紹系統模型，第3節介紹協作網絡編碼實現方案，第4節針對所設計的方案進行系統性能分析，第5節是仿真結果，第6節是總結。

2 非對稱協作傳輸系統模型

假設系統工作在半雙工通信模式，完全同步，信號發送的功率都為P，傳輸信道為瑞利衰落信道。在傳輸的某一個時隙內，信道增益保持不變，且信道參數可通過信道估計準確得到。如圖1所示，假設源節點A發送的信源符號為SA∈ { 0 ,1}K，速率為RA，經過規則RA編碼得到CA∈ { 0,1}N，其碼率為Rc=K/N，再經過調制得到符號XA。同樣，源節點B的信源符號為SB∈ { 0,1}K，碼率為RB，碼字為CB∈ { 0,1}N，調制符號為XB。若節點B通信環境較差，則節點A和中繼R之間的鏈路優于節點A和B之間的鏈路，也優于R和B之間的鏈路。為實現可靠性傳輸，源節點的信源速率必須受其鏈路最大傳輸能力的限制。系統最大能力傳輸時，源節點A的最大信源發送速率RA大于源節點B的速率RB，即RA＞RB。

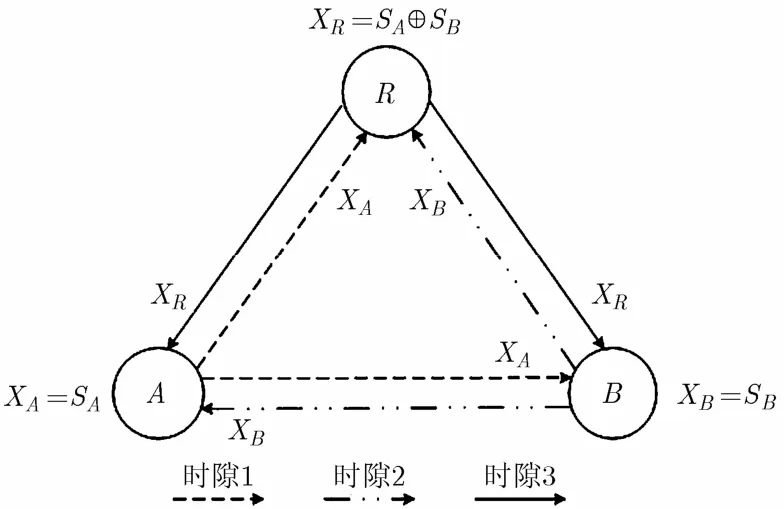
圖1 系統傳輸模型

系統分為3個時隙進行信息交互。在第1個時隙，源節點A將SA編碼調制后的信號XA發送至源節點B和中繼節點R。在源節點B和中繼節點R接收到的信號分別為

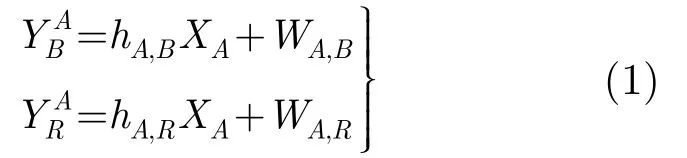
其中hA,B,hA,R分別為其信道增益，WA,B,WA,R是方差為2σ的加性高斯白噪聲。

在第2個時隙，源節點B將SB編碼調制后的信號XB發送至源節點A和中繼節點R。在源節點A和中繼節點R接收到的信號分別為

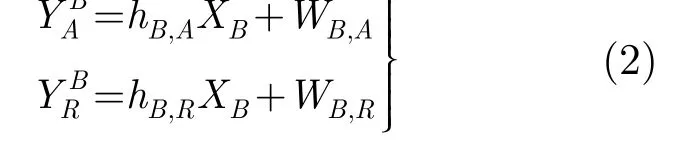
在第3個時隙，中繼對收到的信號解調譯碼得到SA和SB，然后進行編碼、網絡編碼和調制，得到再生信號XR，并將其廣播出去。在源節點A和B接收到的信號分別為

信道上下行對稱：hB,A=hA,B,hB,R=hR,B,hA,R=hR,A。

3 協作網絡編碼方案具體實現

3.1 源節點編碼調制過程

源節點A,B發送信源符號SA,SB，且速率RA＞RB，為了討論方便，假設RA/RB= 3 /2，其他不同速率傳輸的實現方式相似。SA,SB經過相同的規則RA編碼得到碼字CA,CB。文獻[10]給出了規則RA碼編碼器結構，如圖2所示。

圖2 規則RA碼編碼器結構

本文采用規則RA碼進行信道編碼：每次輸入2 bit信息，重復3次，然后進行交織和累加，得到一個6 bit的碼字。將碼字CA按8PSK調制得到發送信號XA，對CB進行QPSK調制得到信號XB。

3.2中繼節點網絡編碼的實現

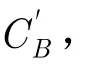
圖3 中繼節點編碼結構

3.3 源節點的譯碼過程

源節點A譯碼設計示于圖4。

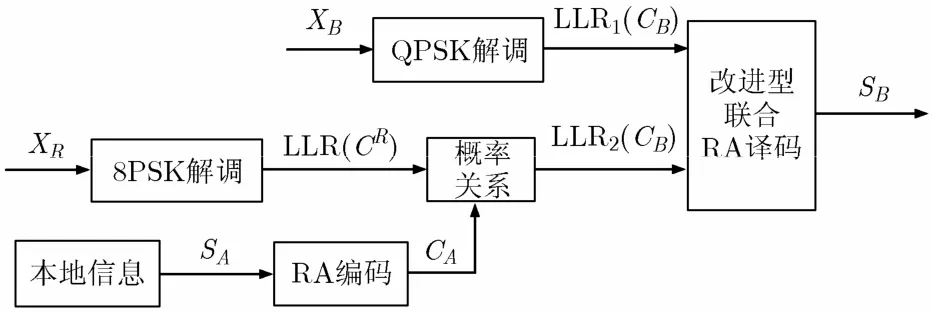
圖4 源節點A譯碼設計

在文獻[11]中給出了1維圓對稱復隨機變量y的概率密 度 分 布 函 數 為f(y)= [1/(πσ2) ]exp( - (a2+ b2)/σ2)，其中a, b為復隨機變量y的實部和虛部。在本文中，在接收端收到一個符號y=x+w=h1x1+w1+j·(h2x2+w2),y是含有高斯白噪聲的復高斯變量，當發送一個符號x，其先驗概率密度為

收到一個符號y，是00調制的概率為p(C=00|y) =f(y|x)p(x) /p(y),p(x),p(y)是已知樣本概率。令常數k=p(x) /p(y)，則有p(C=00|y) =f(y|x)k。其他符號的判決概率可類似求得。

源節點A收到一個符號，其中包含兩位碼字信息，第1位判決為0的概率為，判1的概率

第 1位的對數似然比(Log-Likelihood Ratio,LLR)為

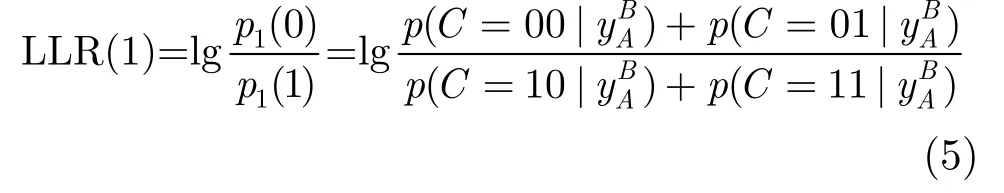
同理可得，第2位的對數似然比為

本文設計的譯碼器每次輸入 6 bit碼字的對數似然比值。根據以上對數似然比的計算公式，可求得碼字中每一位的對數似然比的值。每次譯碼以 3個信號為單位，可計算得到6個對數似然比作為譯碼器的輸入值，設其為 L LR1(CB)。

本文設計的聯合譯碼方案是在常規 BP譯碼算法上改進的。圖5示出了規則RA碼Tanner圖。譯碼過程中，Tanner圖傳遞了4種信息：信息節點u到校驗節點c的傳遞信息m(u,c)；校驗節點c到信息節點u的信息m(c,u)；校驗節點c到奇偶節點y的信息m(c,y)；奇偶節點y到校驗節點c的信息m(y,c)。兩個對數似然比輸入的聯合RA譯碼算法步驟如下：

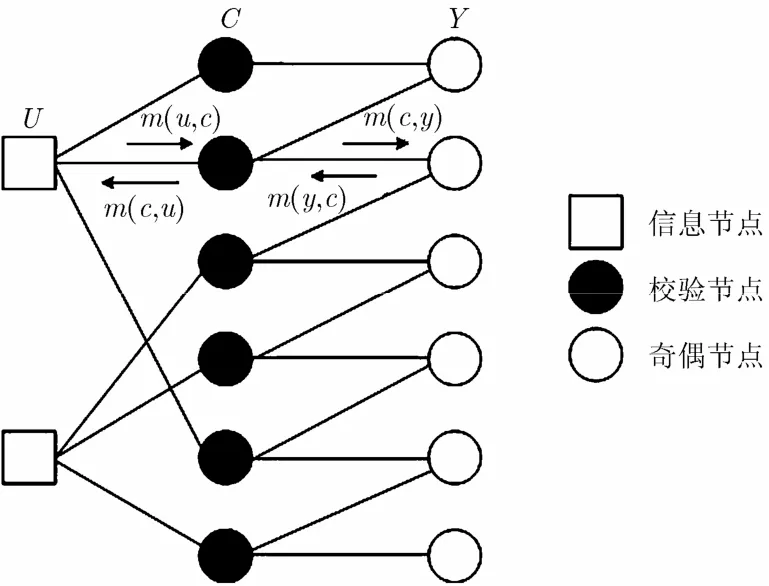
圖5 規則RA碼Tanner圖

步驟1 初始化邊傳遞信息m(u,c),m(c,u),m(c,y),m(y,c)為零，設定常數K為迭代次數。輸入LLR1(CB)準備譯碼迭代。

步驟2 更新變量節點：

更新校驗節點，

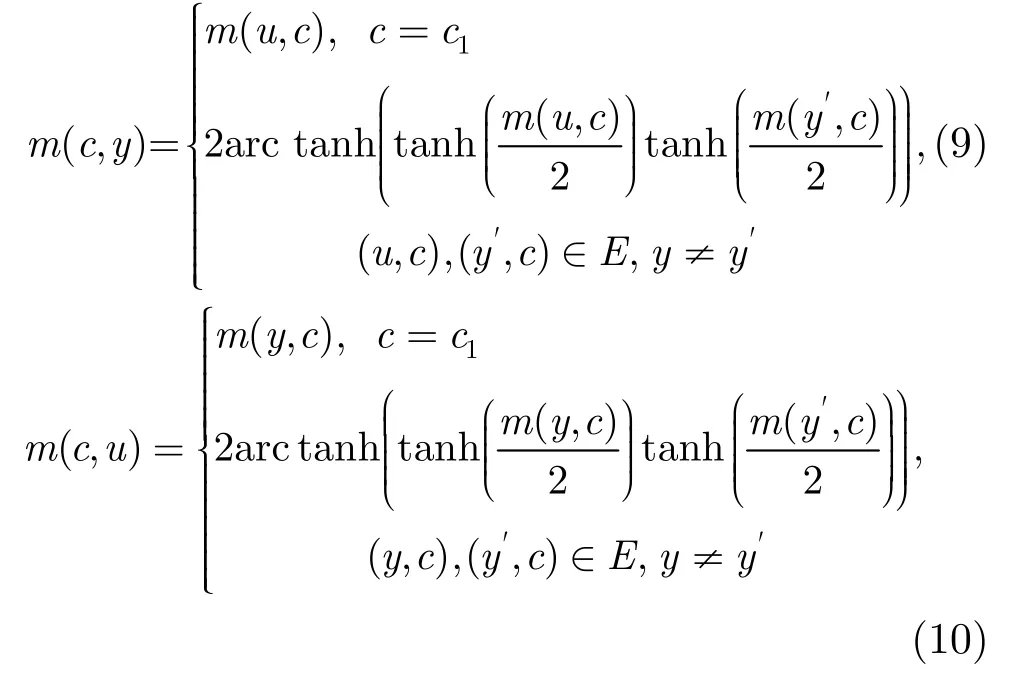
迭代完畢，對每個信息節點u∈U，計算s1(u)=∑cm(u,c)。

步驟3 重復步驟1和步驟2，不同的是此時把LLR1(CB)替換成 L LR2(CB)作為譯碼輸入。然后迭代得到s2(u) = ∑cm(u,c)。

步驟4 判決：s(u) =s1(u) +s2(u)，如果s(u)≥0，則位u的譯碼值為0，否則為1。

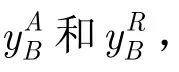
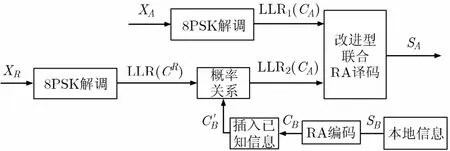
圖6 源節點B譯碼設計

4 非對稱協作分集網絡編碼的中斷性能分析

在無線通信系統中，衡量通信系統的可靠性是通過中斷概率來衡量的。文獻[12]中提到，在給定系統要求傳輸速率條件下，中斷事件發生的概率就是中斷概率。表示為：pout=p(IA,B＜Rb) ,IA,B是源節點A和B之間交互的互信息，Rb為系統要求的傳輸速率。

在本文中，假設節點A和B的直接鏈路發生中斷的概率為pout(AB)，節點A和中繼R發生中斷的概率為pout(AR)，節點B和中繼R發生中斷的概率為pout(BR)。由此可得，節點A、中繼R和節點B這 3個節點之間的通信鏈路的中斷概率pout(ARB)為

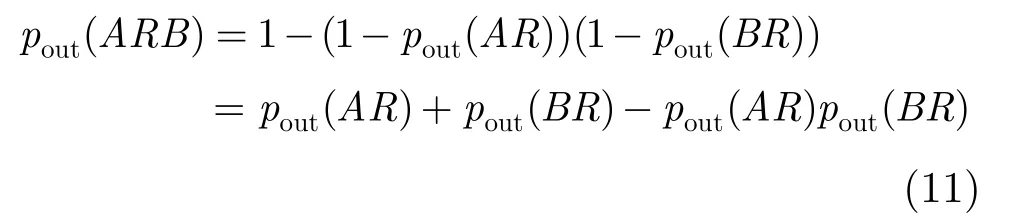
整個協作分集系統的中斷概率pout(Sys)為

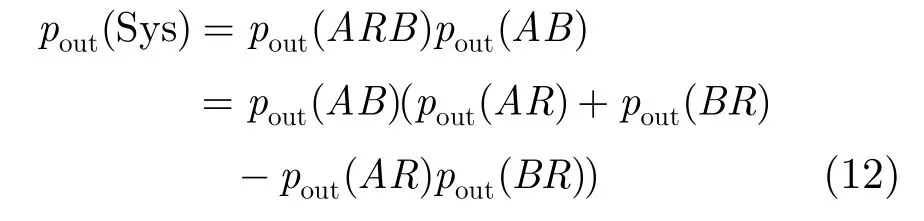
其他通信節點的中斷率類似可得。整個系統的中斷概率為

5 系統仿真結果分析

仿真采用瑞利衰落信道，在傳輸某一個時隙內，其信道增益保持不變，且信道參數可通過信道估計準確得到，系統工作在半雙工模式，信號發送功率相同。圖7給出源節點B中，本文設計的非對稱速率與傳統對稱速率傳輸之間的誤比特率比較。由于較差鏈路的限制，為了保證可靠性，對稱傳輸只能采用較差鏈路允許的最大速率進行數據傳輸，即系統只能采用 QPSK-QPSK方案。如果采用 8PSK-8PSK對稱傳輸方案，則較差鏈路將不能保證其可靠性。由圖中可以看出本文設計的QPSK-8PSK非對稱傳輸系統比QPSK-QPSK對稱傳輸系統誤比特率略高，但優于8 PSK-8 PSK傳輸方案，能保證傳輸的可靠性。從圖8可以看出，在存在中繼鏈路的協作分集傳輸系統中，誤比特率低于傳統的非協作系統。因此，利用協作分集能提高譯碼的準確性，即協作通信更能保證傳輸系統的可靠性。

圖9給出非對稱和對稱傳輸系統信道容量的比較。仿真時較差、較優鏈路的信噪比分別相差2 dB和4 dB。仿真結果表明，本文所提機制信道容量比傳統對稱傳輸方案略有提高。為了衡量信道容量提升的幅度，仿真時定義了一個相對容量增長率：r= (CQ8-CQQ) /CQQ,CQ8表示非對稱傳輸系統的信道容量，CQQ表示采用可靠對稱傳輸 QPSKQPSK方案的信道容量。r越大，表明非對稱系統相對于對稱系統容量的提升越明顯。圖10給出了較差、較優鏈路的信噪比分別相差2 dB, 3 dB和4 dB時r的數值曲線。從圖中可以看出，源節點通信環境差異越大，采取非對稱傳輸的相對容量增長率越大，即系統容量的提升越顯著。

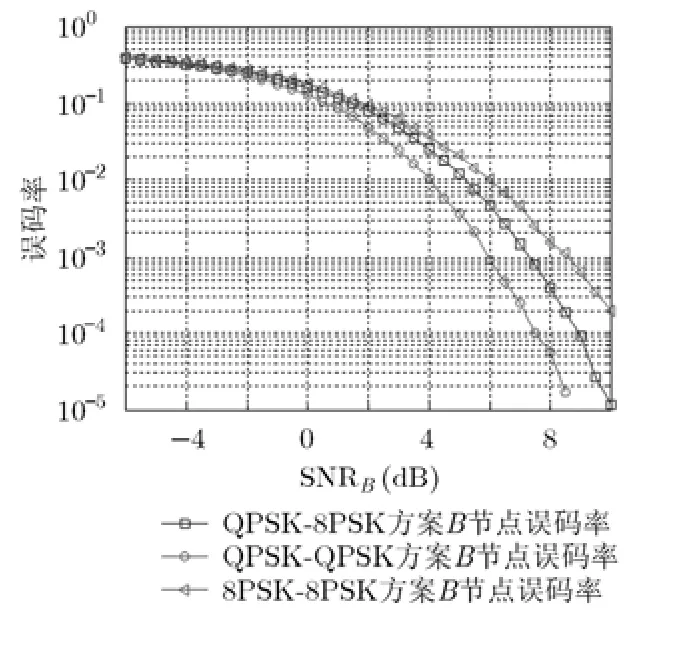
圖7 對稱與非對稱速率傳輸誤比特率比較

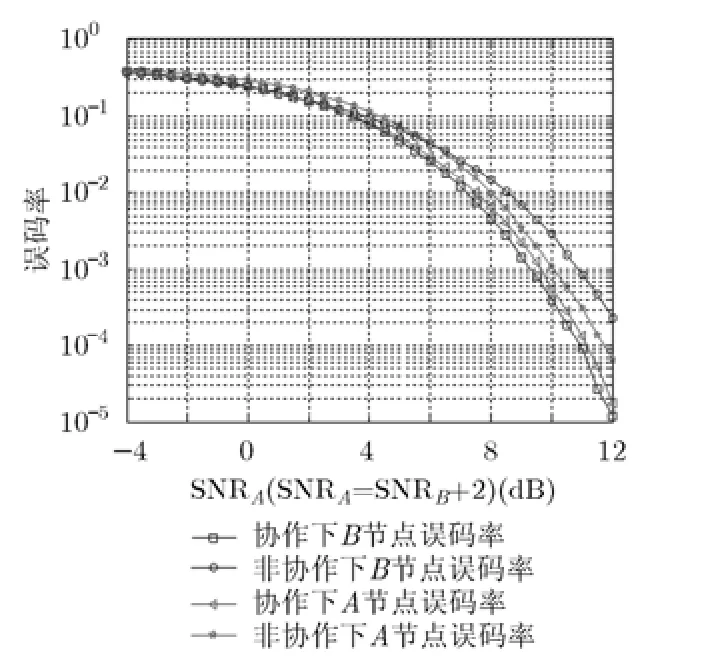
圖 8 協作與非協作分集的誤碼率比較

圖9 不同調制系統的信道容量比較

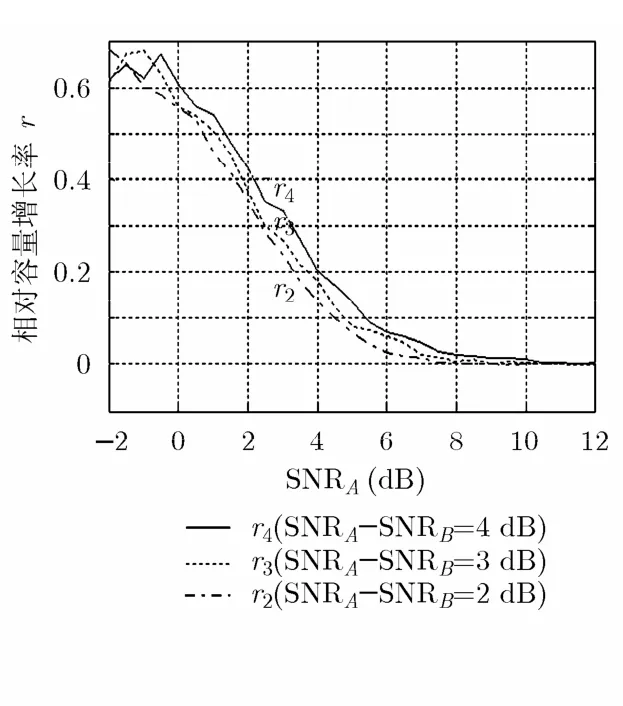
圖10 差異信道下容量的相對增長趨勢

圖11 非對稱協作分集系統中斷率圖

同時，為了說明設計的系統能實現傳輸的連續性，圖11給出了所設計系統的中斷概率曲線，其中Rb是系統要求的傳輸速率。由曲線可看出，在瑞利衰落信道中采取非對稱傳輸，其中斷概率能得到保證。

6 結束語

本文研究了非對稱速率協作分集系統中網絡編碼的實現。在無線通信差異環境中，考慮鏈路狀況不一，利用非對稱傳輸方式既可保證通信系統中較差鏈路傳輸的可靠性，同時又能利用較優鏈路傳輸更多的信息。相比較傳統的對稱傳輸，系統的資源得到了更充分的利用。同時，把分集技術和網絡編碼技術結合，在得到增加系統分集增益的同時，還能得到編碼增益。在源節點譯碼中采用兩個信息副本的聯合譯碼的改進算法，增加了譯碼的準確性。

[1]Ahlswede R, Cai N, Li S Y,et al.. Network information flow[J].IEEE Transactions on Information Theory, 2000,46(4): 1204-1216.

[2]Xiao L, Fuja T, Kliewre J,et al.. A network coding approach to cooperative diversity[J].IEEE Transations on Information Theory, 2007, 53(10): 3714-3722.

[3]Nosratinia A, Hunter T, and Hedayat A. Cooperative communication in wireless networks[J].IEEE Communications Magazine, 2004, 42(10): 74-80.

[4]Rebelatto J L, Ucho＾oa - Filho B F, Li Y,et al.. Multi-user cooperative diversity through network coding based on classical coding theory[J].IEEE Transactions on Signal Processing, 2012, 60(2): 916-926.

[5]Sharma Sushant, Shi Yi, Liu Jia,et al.. Network coding in cooperative communications: friend or foe?[J].IEEE Transactions on Mobile Computing, 2012, 11(7): 1073-1085.

[6]Hou J, Hausl C, and Kotter R. Distributed turbo coding schemes for asymmetric two way relay communication[C].IEEE International Workshop on Turbo Codes and Related Topics (ICC), USA, Sept. 2008: 237-242.

[7]Zhao Jian, Kuhn M, Wittneben A,et al.. Asymmetric data rate transmission in two-way relaying systems with network coding[C]. IEEE International Conference on Communications (ICC), USA, 2010: 1-6.

[8]Divsalar D, Jin H, and McEliece R. Coding theorems for turbo-like codes[C]. Proceedings of the 36th Annual Allerton Conference on Communication Control and Computing,Monticello, IL, USA, 1998, 9: 201-210.

[9]朱聯祥, 李祥, 行彥輝, 等. 重復累計碼在協作分集系統中的應用研究[J]. 重慶郵電大學學報(自然科學版), 2011, 23(1):16-20.

Zhu Lian-xiang, Li Xiang, Xing Yan-hui,et al.. Application of repeat-accumulate code in the cooperative system[J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2011, 23(1): 16-20.

[10]高宏峰, 許宗澤. RA碼譯碼簡化算法的研究[J]. 四川大學學報 (工程科學版), 2004, 36(4): 107-110.

Gao Hong-feng and Xu Zong-ze. Reduced complexity decoding algorithms for repeat accumulate codes[J].Journal of Sichuan University(Engineering Science Edition), 2004,36(4): 107-110.

[11]仇佩亮. 信息論與編碼[M]. 北京: 高等教育出版社, 2003:165-170.

Qiu Pei-liang. Information Theory and Coding[M]. Beijing:High Education Press, 2003: 165-170.

[12]吉曉東, 鄭寶玉. 物理層網絡編碼機會中繼及中斷性能分析[J]. 電子與信息學報, 2011, 33(5): 1186-1192.

Ji Xiao-dong and Zheng Bao-yu. Opportunistic relaying and outage analysis for physical-layer network coding [J].Journal of Electronics&Information Technology, 2011, 33(5):1186-1192.