四元數(shù)域彩色圖像整體式水印算法
孫 菁 楊靜宇
①(南京信息工程大學(xué)濱江學(xué)院 南京 210044)
②(南京理工大學(xué)計(jì)算機(jī)科學(xué)與技術(shù)學(xué)院 南京 210094)
1 引言
數(shù)字水印(digital watermarking)技術(shù)作為數(shù)字媒體作品知識(shí)產(chǎn)權(quán)保護(hù)的一種有效手段得到了廣泛關(guān)注。目前大多數(shù)以靜止圖像為載體的水印算法都是針對(duì)灰度圖像的,現(xiàn)有的針對(duì)彩色圖像的水印算法,一般都是通過(guò)顏色模型轉(zhuǎn)換,將彩色圖像劃分為各獨(dú)立通道(RGB, HSV, YCbCr等等),使用其中的某一通道(最常用的就是亮度通道[1]和藍(lán)色人眼視覺(jué)不敏感通道[2])來(lái)進(jìn)行水印的嵌入;要么對(duì)上述方法稍微擴(kuò)展,在組成彩色圖像的所有色彩通道中分別嵌入水印后再進(jìn)行加成[3]。縱觀以上兩類(lèi)方法,要么沒(méi)有完整利用彩色圖像所有信息,要么將彩色圖像信息分割開(kāi),不能體現(xiàn)彩色通道間的聯(lián)系,本質(zhì)上都是灰度圖像處理方法的擴(kuò)展。
由于彩色圖像的各色彩通道之間存在著強(qiáng)烈的光譜聯(lián)系,如果把一個(gè)彩色像素作為一個(gè)整體來(lái)處理,那么像素各色彩通道間的光譜聯(lián)系就會(huì)貫穿在對(duì)這個(gè)整體進(jìn)行運(yùn)算、處理的過(guò)程中。在對(duì)彩色圖像整體式處理方法的研究中,文獻(xiàn)[4]首先引入了四元數(shù)概念。四元數(shù)把三色空間上的彩色圖像視為一個(gè)矢量整體進(jìn)行描述,在運(yùn)算空間以及保留彩色圖像各通道間的相互關(guān)系上具有很大優(yōu)勢(shì)。該數(shù)學(xué)模型最早由文獻(xiàn)[5]應(yīng)用在了數(shù)字水印領(lǐng)域,文中使用已有的量化索引調(diào)制方法對(duì)四元數(shù)傅里葉變換(Quaternion Fourier Transform, QFT)在彩色圖像水印中的應(yīng)用進(jìn)行了嘗試,給出了四元數(shù)傅里葉變換最優(yōu)參數(shù)。其后,文獻(xiàn)[6]根據(jù)四元數(shù)域元素的特點(diǎn)設(shè)計(jì)了視覺(jué)掩模,將水印隱藏到彩色圖像四元數(shù)傅里葉變換系數(shù)中,文獻(xiàn)[7]將水印隱藏到四元數(shù)傅里葉系數(shù)的實(shí)部,文獻(xiàn)[8]將水印隱藏到四元數(shù)傅里葉系數(shù)的幅值中,通過(guò)實(shí)驗(yàn)驗(yàn)證了相同嵌入容量下,四元數(shù)域算法確實(shí)具有比傳統(tǒng)亮度域算法更好的魯棒性。但是,由于基于四元數(shù)理論的彩色圖像水印技術(shù)在國(guó)內(nèi)的研究尚處于起步階段,上述算法在設(shè)計(jì)中也難免存在一些疏漏,如對(duì)相同嵌入容量下,四元數(shù)域算法相對(duì)于傳統(tǒng)算法的不可見(jiàn)性并未進(jìn)行論證,并且,也并未對(duì)一些安全性問(wèn)題,如:誤檢測(cè)率、易偽造性等進(jìn)行考證。針對(duì)這個(gè)情況,本文在前人研究基礎(chǔ)上,提出一種結(jié)合四元數(shù)變換域以及分解理論為一體的四元數(shù)頻域奇異值分解彩色圖像水印算法。首先對(duì)彩色載體圖像進(jìn)行分塊四元數(shù)傅里葉變換得到其頻域矩陣,然后對(duì)頻域單位小塊進(jìn)行四元數(shù)奇異值分解,根據(jù)分解得到四元數(shù)酉矩陣前若干列中對(duì)角線元素的幅值構(gòu)造水印序列,將水印隱藏到分解得到的實(shí)系數(shù)奇異值中。仿真實(shí)驗(yàn)表明,對(duì)彩色圖像采用四元數(shù)模型進(jìn)行整體式奇異值分解并嵌入水印的方法的確比同樣步驟下單獨(dú)通道方法得到的水印圖像失真更小;并且通過(guò)在算法中增加奇異值分解過(guò)程,構(gòu)造與奇異值酉矩陣相關(guān)的水印序列可以有效解決已有同類(lèi)算法存在的誤檢測(cè)率問(wèn)題。
2 彩色圖像的四元數(shù)相關(guān)理論
2.1 彩色圖像的四元數(shù)描述
四元數(shù)是復(fù)數(shù)在4維實(shí)空間的不可交換延伸,其理論體系早在19世紀(jì)40年代初由愛(ài)爾蘭數(shù)學(xué)家Hamilton創(chuàng)立,但在相當(dāng)長(zhǎng)的一段時(shí)間里沒(méi)有為人們所重視。直到1996年,英國(guó)科學(xué)家Todd, Ell和Sangwine提出了彩色圖像的四元數(shù)模型,四元數(shù)在彩色圖像上的應(yīng)用研究開(kāi)始發(fā)展。
一個(gè)四元數(shù)可以表示為

式中a0,a1,a2,a3為實(shí)數(shù),i,j,k為虛數(shù)單位,i,j,k之間的聯(lián)系定義為

從上述定義可以看出,四元數(shù)的乘法不滿足交換律。
對(duì)于由RGB色彩模型表示的彩色圖像f,可以用實(shí)部為零的純虛四元數(shù)fq= Ri+ Gj+ Bk進(jìn)行表示,其中R, G, B分別表示彩色圖像紅、綠、藍(lán)3種顏色分量的亮度值。
2.2 四元數(shù)傅里葉變換
四元數(shù)域的傅里葉變換因四元數(shù)乘法的非交換性而不能套用實(shí)數(shù)矩陣的常規(guī)方法來(lái)解決,Todd和Sangwine使用一種“平行(simplex)垂直(perplex)分解”變換法將待變換的四元數(shù)分解成平行于某個(gè)任意選定的單位純虛四元數(shù)μ1的復(fù)數(shù)分量A和垂直于μ1的二次復(fù)數(shù)分量Bμ2,將四元數(shù)傅里葉變換轉(zhuǎn)化為二次復(fù)數(shù)的傅里葉變換問(wèn)題。求解公式如式(3)[9]:

計(jì)算四元數(shù)傅里葉逆變換需要按同樣的原理,先將四元數(shù)函數(shù)Fq(u,v)沿μ1分解成兩個(gè)二次復(fù)數(shù):平行分量A′和垂直分量B′μ2,則逆變換有
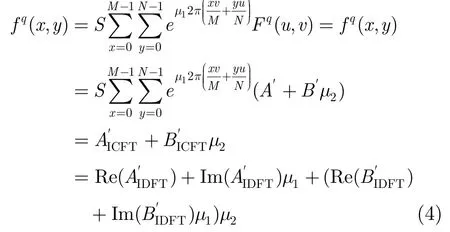
式中,ICFT, IDFT分別表示復(fù)數(shù)和實(shí)數(shù)傅里葉逆變換。四元數(shù)傅里葉逆變換問(wèn)題也轉(zhuǎn)變成實(shí)數(shù)離散傅里葉逆變換的代數(shù)運(yùn)算。
2.3彩色圖像的四元數(shù)奇異值分解及其性質(zhì)
2.3.1 四元數(shù)奇異值分解理論奇異值分解 SVD(Singular Value Decomposition)理論早在20世紀(jì)70年代首先提出,奇異值良好的穩(wěn)定性使得該理論在灰度圖像處理中得到了廣泛的應(yīng)用。近年來(lái),將奇異值分解理論擴(kuò)展到四元數(shù)領(lǐng)域得到的四元數(shù)奇異值分解 QSVD(Quaternion SVD)理論使得原本只適用于灰度圖像的奇異值分解技術(shù)可以推廣到彩色圖像中。
然而,由于四元數(shù)乘法的不可交換性,四元數(shù)矩陣的奇異值分解與實(shí)數(shù)矩陣不太一樣,文獻(xiàn)[10]對(duì)四元數(shù)奇異值分解進(jìn)行了實(shí)踐探索,它認(rèn)為對(duì)于任何n×n階四元數(shù)矩陣Qq,若矩陣的秩rank(Q)=r,則存在四元數(shù)酉矩陣Uq和Vq,使得Qq=UqΣ(Vq)H,其中Uq(Uq)H=Vq(Vq)H=I,Uq和Vq的列向量分別被稱(chēng)為Qq的左右特征向量,而

且滿足σi∈R,|σ1|≥|σ2|≥ … ≥|σr|>0。
2.3.2四元數(shù)奇異值分解的性質(zhì)實(shí)系數(shù)矩陣奇異值分解理論在灰度圖像處理領(lǐng)域通常表現(xiàn)出如下性質(zhì):
(1)矩陣與奇異值之間的多對(duì)一性質(zhì)。一個(gè)矩陣的奇異值是確定的,但不同矩陣可以有相同的奇異值。
(2)圖像的幾何和紋理信息都集中在奇異值分解得到的U,V矩陣中,而奇異值矩陣S則表示圖像的能量信息。
(3)對(duì)圖像質(zhì)量起主要影響作用的是U,V矩陣前若干列和對(duì)角陣S的前若干個(gè)元素。
(4)U,V矩陣前若干列以及奇異值矩陣S的前若干個(gè)元素具有較強(qiáng)穩(wěn)定性,對(duì)一些常見(jiàn)圖像處理表現(xiàn)出一定魯棒性。
(5)奇異值矩陣各元素間遵循從大到小降序排列的規(guī)律并且衰減很快。
在研究彩色圖像四元數(shù)奇異值分解性質(zhì)中,我們還發(fā)現(xiàn)了幾點(diǎn)沒(méi)有經(jīng)過(guò)公開(kāi)討論的性質(zhì),列出于性質(zhì)(6),性質(zhì)(7)。
(6)分解具有明顯特征的矩陣時(shí),得到的U,V矩陣也具有一定特征。如圖像經(jīng)傅里葉時(shí)頻變換后得到的頻率矩陣,低頻部分位于四角,高頻部分位于中心,對(duì)具有這樣特征的矩陣進(jìn)行奇異值分解,得到的U,V矩陣也將具有一定規(guī)律:即U,V矩陣的高能量區(qū)域集中在圖像的主對(duì)角線和次對(duì)角線周邊區(qū)域內(nèi),而U,V矩陣的低能量區(qū)域集中在矩陣的第1行以及第1列(除去U(1,1),V(1,1))。圖1以Cafet圖像為例,顯示了這條規(guī)律。
(7)對(duì)于彩色圖像而言,性質(zhì)(2)不成立。
證明如下:
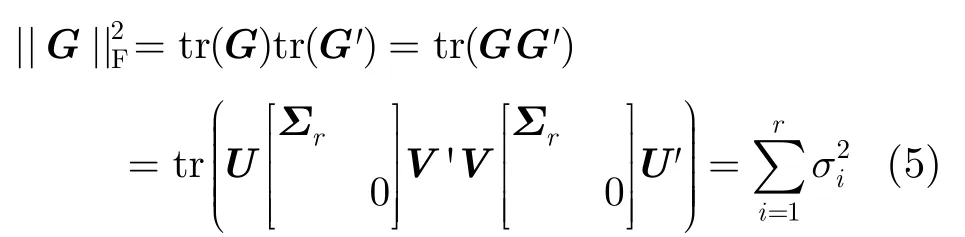
式(5)成立的前提為:任意實(shí)數(shù)域矩陣A,B,存在(AB)'=B' A'。然而,對(duì)于四元數(shù)域上的任意矩陣Aq和Bq,等式(Aq Bq)'=Bq'Aq'不成立,證明如下。

圖1 Cafet圖像的傅里葉域奇異值矩陣幅值特性圖
這就說(shuō)明彩色圖像能量不僅只和奇異值有關(guān),還應(yīng)當(dāng)與四元數(shù)奇異值酉矩陣有關(guān),四元數(shù)矩陣奇異值分解得到的左右四元數(shù)酉矩陣應(yīng)當(dāng)比在各獨(dú)立通道上進(jìn)行實(shí)系數(shù)矩陣奇異值分解,然后再將各通道分解得到的矩陣合成后得到的多重實(shí)系數(shù)矩陣包含的信息更為復(fù)雜。可以進(jìn)一步推論,如果僅改變彩色圖像奇異值,維持奇異值矩陣不變,四元數(shù)方法得到的圖像失真度應(yīng)當(dāng)小于多通道合成的方法。
2.3.3 奇異值水印算法分析利用奇異值分解在圖像中嵌入水印的策略是由Liu等人[11]較早提出,算法利用奇異值良好的穩(wěn)定性獲得了抗攻擊性能非常優(yōu)秀的魯棒水印圖像。
然而通過(guò) 2.3.2節(jié)對(duì)奇異值分解性質(zhì)的分析不難發(fā)現(xiàn),上述一類(lèi)算法在利用奇異值良好穩(wěn)定性的同時(shí)也引入不少缺陷,使算法安全性大大下降。
(1)嵌入水印時(shí),沒(méi)有考慮到矩陣與奇異值之間的多對(duì)一性質(zhì)即不同圖像的奇異值可能接近甚至相同的問(wèn)題,提取水印時(shí)又僅在奇異值中展開(kāi),用到的信息并不能完全代表水印圖像本身,從而導(dǎo)致對(duì)隨機(jī)選取圖像的虛警率比較高;
(2)偽造水印圖像方便,安全性差。由于圖像信息主要集中在奇異值U,V矩陣和最大奇異值 S1中,且奇異值衰減很快,不同圖像的奇異值除前若干個(gè)外均比較接近,導(dǎo)致只要能夠獲得任意含水印圖像作品,就可以方便地將任意選取的圖像偽造成滿足一定不可見(jiàn)性和魯棒性的水印圖像;
(3)嵌入水印時(shí),人為改變奇異值大小不會(huì)改變重構(gòu)再分解后奇異值間的降序排列順序,這樣,在檢測(cè)水印時(shí)就需要原始圖像的參與,不能做到盲檢測(cè)。
文獻(xiàn)[12],文獻(xiàn)[13]對(duì)缺陷(1),缺陷(2)進(jìn)行了比較詳細(xì)的實(shí)驗(yàn)討論,然而,他們并沒(méi)有給出很好的解決方案,此后很多學(xué)者在文獻(xiàn)[11]研究基礎(chǔ)上提出了自己的基于奇異值分解的水印算法[14],側(cè)重點(diǎn)還是在不可見(jiàn)性基礎(chǔ)上追求更高的魯棒性,上述問(wèn)題并沒(méi)有得到很好的重視和解決。
3 彩色圖像四元數(shù)頻域奇異值分解水印算法
眾多奇異值分解水印算法存在的安全問(wèn)題歸根到底還是因?yàn)樗惴▋H用到了水印圖像的奇異值信息而沒(méi)有考慮對(duì)圖像影響占重要地位的U,V矩陣,本文以此為切入點(diǎn),構(gòu)造一個(gè)與原始彩色圖像QSVD分解得到四元數(shù)矩陣U,V有關(guān)的向量作為水印序列,在保證不可見(jiàn)性和魯棒性折中的前提下,有效地提高算法的安全性。
3.1 水印的嵌入
為了方便起見(jiàn),我們假設(shè)原始載體圖像矩陣為方陣,對(duì)于長(zhǎng)寬不等的非正方形圖像,本文算法同樣適用。
(1)將大小為M×M的原始載體彩色圖像按一定大小n分塊(為方便起見(jiàn),n一般取為M的因子),取得無(wú)重疊的N=(M/n)2個(gè)小塊;
(4)取出該塊中介于最大和最小位置之間連續(xù)k個(gè)奇異值作為嵌入位置以取得不可見(jiàn)性和魯棒性的折中;
(6)重復(fù)步驟(3)-步驟(5)修改完所有的分塊,對(duì)修改后的分塊進(jìn)行四元數(shù)傅里葉反變換,將所有分塊合成后得到水印圖像。
3.2 水印的檢測(cè)
在這個(gè)步驟中,不需要原始載體圖像參與,可以視為一種盲檢測(cè)方法。需要提供原始圖像分塊奇異值對(duì)角陣Si, 1≤i≤N作為密鑰,步驟如下:
(1)對(duì)待檢測(cè)圖像按嵌入水印時(shí)的同樣大小分塊;
(2)依次取出每一個(gè)分塊,對(duì)其四元數(shù)傅里葉變換后接著進(jìn)行四元數(shù)奇異值分解;
(4)按照嵌入時(shí)的位置取出該分塊分解得到的k個(gè)奇異值,提取密鑰Si中相應(yīng)位置奇異值Sij,計(jì)算嵌入的水印。對(duì)所有分塊都進(jìn)行同樣的操作,將N個(gè)順序連接起來(lái),得到實(shí)際嵌入的水印序列W';
(5)計(jì)算WUV和W'兩者的歸一化相關(guān)系數(shù)Corr;
(6)設(shè)置適當(dāng)閾值T,當(dāng)Corr>T時(shí)判定為存在水印,否則判定為沒(méi)有水印。
4 實(shí)驗(yàn)結(jié)果與分析
在仿真實(shí)驗(yàn)中,首先選取 512×512大小的Avion, Lena和House 3幅彩色載體圖像來(lái)測(cè)試算法的不可見(jiàn)性和魯棒性。嵌入水印時(shí)使用到的參數(shù)如下:圖像分塊大小16×16,共取得N=(512/16)2=1024個(gè)小塊,每塊取其中的第2-第7個(gè)奇異值作為嵌入位置,即k=6, 2≤j≤7,主成份列X=2,全局能量調(diào)節(jié)系數(shù)γ取0.8,下面給出實(shí)驗(yàn)結(jié)果和分析。
4.1 不可見(jiàn)性
我們?cè)?.3.2節(jié)QSVD分解性質(zhì)(7)中表明,對(duì)于彩色圖像水印, 維持奇異值矩陣不變,僅改變圖像奇異值大小,四元數(shù)方法得到的圖像失真度應(yīng)當(dāng)小于多通道合成的方法。圖2中實(shí)驗(yàn)數(shù)據(jù)很好地說(shuō)明了這一觀點(diǎn),圖中獨(dú)立多通道方法指的是和本文算法具有相同嵌入步驟、嵌入容量,但使用獨(dú)立多通道來(lái)實(shí)現(xiàn)水印嵌入,最后將各通道結(jié)果合成的方法,圖中所列數(shù)字為傳統(tǒng)衡量圖像質(zhì)量用到的PSNR值。
觀察兩種方法獲得的水印圖像,在使用相同的全局能量調(diào)節(jié)系數(shù)調(diào)節(jié)的情況下,都能滿足不可見(jiàn)性并且人眼視覺(jué)效果沒(méi)有太大差別。但是比較二者PSNR值,四元數(shù)方法高于多通道合成方法,說(shuō)明了本文方法獲得的水印圖像的失真度確實(shí)比后一種方法要小。
4.2 魯棒性
一個(gè)良好的水印算法在滿足不可見(jiàn)性的同時(shí),還必須滿足一定的魯棒性。表1給出了算法對(duì)幾種常見(jiàn)無(wú)意攻擊的檢測(cè)相關(guān)系數(shù)。
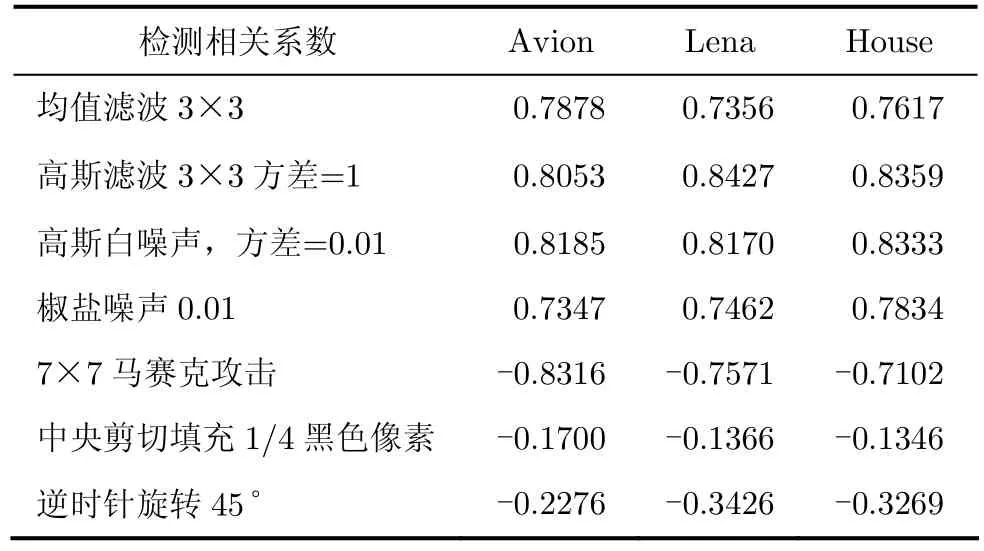
表1 攻擊-檢測(cè)相關(guān)系數(shù)表
可以看出,由于奇異值和奇異值酉矩陣的穩(wěn)定性,算法對(duì)一些常見(jiàn)非同步無(wú)意攻擊的檢測(cè)相關(guān)系數(shù)值是較高的,但對(duì)剪切和旋轉(zhuǎn)等攻擊的魯棒性較差,這主要是因?yàn)樵陬?lèi)似的幾何攻擊中,用于產(chǎn)生水印的U,V矩陣發(fā)生了比較大的變化。
4.3 誤檢率
最后比較本文算法與文獻(xiàn)[11](這里我們將文獻(xiàn)[11]的方法擴(kuò)展到四元數(shù)域進(jìn)行)以及文獻(xiàn)[6-8]算法的誤檢測(cè)率。實(shí)驗(yàn)過(guò)程如下:首先,選擇圖像數(shù)據(jù)庫(kù)中任意一幅彩色圖像,分別使用本文算法和上述4種算法嵌入水印,然后在圖像數(shù)據(jù)庫(kù)中任意選擇若干幅大小相同,類(lèi)型不同的無(wú)水印彩色圖像,使用上述幾種算法的提取水印過(guò)程依次對(duì)這些圖像進(jìn)行提取水印操作,最后比較提取出的信息和嵌入水印之間的歸一化相關(guān)系數(shù)。為了保證嵌入能量相當(dāng),我們合理調(diào)整了算法中的嵌入強(qiáng)度系數(shù),使得幾種方法得到的水印圖像的 PSNR值大致相當(dāng)。以Avion彩色圖像為例,實(shí)驗(yàn)結(jié)果如下:

圖2 水印圖像不可見(jiàn)性對(duì)比結(jié)果
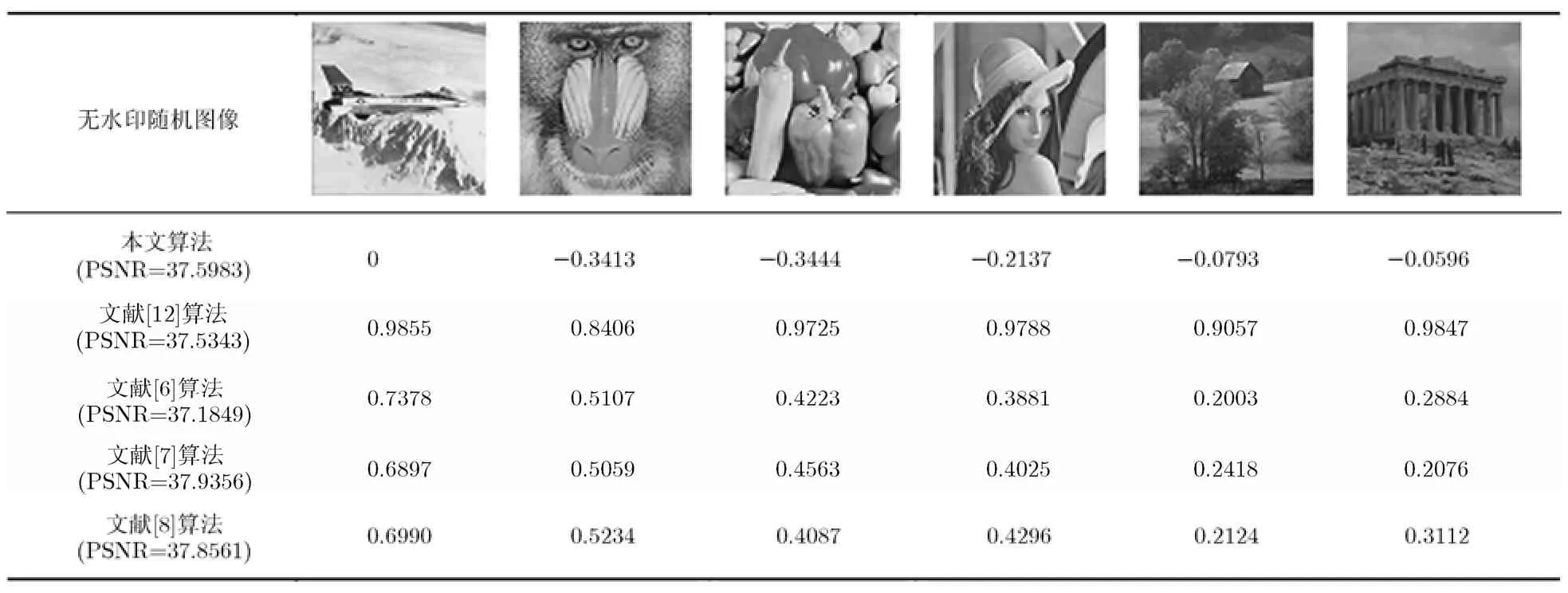
表2 Avion水印圖像的檢測(cè)相關(guān)系數(shù)
5 結(jié)論
由于缺少彩色像素的整體處理方式,對(duì)彩色圖像水印的研究一直以來(lái)遵循灰度圖像處理方式,沒(méi)能很好地利用彩色圖像全部信息。而已有為數(shù)不多的四元數(shù)水印算法在設(shè)計(jì)上,過(guò)于強(qiáng)調(diào)魯棒性,缺少對(duì)不可見(jiàn)性、安全性的細(xì)致考慮,造成誤檢率高以及水印圖像易于偽造等現(xiàn)象。本文提出一種結(jié)合四元數(shù)變換域和分解方法的安全水印方法,主要研究工作包括:(1)首次提出并通過(guò)理論以及實(shí)驗(yàn)數(shù)據(jù)證明對(duì)于彩色圖像水印,使用相同處理步驟嵌入相同容量的水印信號(hào),四元數(shù)方法得到的水印圖像失真度要小于彩色圖像水印傳統(tǒng)方案中使用的多通道方法;(2)本文提出的四元數(shù)變換域結(jié)合奇異值分解的方法水印方案獲得了比一般變換域算法更好的安全性。算法首先采用四元數(shù)模型來(lái)表示彩色圖像像素,由于四元數(shù)傅里葉變換問(wèn)題的解決,設(shè)計(jì)時(shí)將所有處理放在頻域進(jìn)行,使得算法具有一切頻域水印算法的優(yōu)點(diǎn)。接著通過(guò)構(gòu)造一個(gè)與原始圖像QSVD分解得到四元數(shù)矩陣U,V有關(guān)的向量來(lái)作為水印序列,在檢測(cè)時(shí)將提取的水印和由水印圖像QSVD分解的四元數(shù)奇異值矩陣U',V'構(gòu)成的水印序列進(jìn)行相關(guān)計(jì)算,從而判定水印的歸屬,在增加水印與圖像相關(guān)程度的同時(shí)大大降低了對(duì)隨機(jī)選取圖像的虛警率,并且使得偽造水印圖像難以進(jìn)行;(3)由于數(shù)字圖像的奇異值矩陣S和奇異值酉矩陣U,V對(duì)常見(jiàn)處理表現(xiàn)出優(yōu)秀的穩(wěn)定性,算法在檢測(cè)時(shí)用水印圖像 QSVD 分解的矩陣U',V'來(lái)替代原始圖像的U,V矩陣,從而實(shí)現(xiàn)了盲檢測(cè)。實(shí)驗(yàn)驗(yàn)證,本文算法確實(shí)在表現(xiàn)彩色像素、獲得失真更小的水印圖像方面優(yōu)于傳統(tǒng)方法,在虛警率方面優(yōu)于已有的四元數(shù)水印算法。基于四元數(shù)理論的彩色圖像處理技術(shù)在國(guó)內(nèi)的研究尚處于起步階段,本文的工作對(duì)四元數(shù)在彩色圖像處理中的應(yīng)用是很好的補(bǔ)充,為彩色圖像的版權(quán)保護(hù)提供了一種新方法。
[1]Hussein J A. Spatial domain watermarking scheme for colored images based on log-average luminance[J].Journal of Computing, 2010, 2(1): 100-103.
[2]Findik O, Babaolu I,andlker E. A color image watermarking scheme based on artificial immune recognition system[J].Expert Systems with Applications, 2011, 38(3):1942-1946.
[3]Gakkhar D, Samant S, Sharma V,et al.. Compression resistant multichannel color image watermarking[C].International Conference on Signal and Image Processing,Shanghai, China, 2010: 23-28.
[4]Sangwine S J. Fourier transforms of colour images using quaternion, or hypercomplex, numbers[J].Electronic Letter,1996, 32(21): 1979-1980.
[5]Patrick B, Nicolas L B, and Chassery J M. Color image watermarking using quaternion Fourier transform[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing, Hong Kong, China, 2003: 521-524.
[6]Tsui T K, Zhang X P, and Androutsos D. Color image watermarking using multidimensional Fourier transforms[J].IEEE Transactions on Information Forensics and Security,2008, 3(1): 16-28.
[7]江淑紅, 張建秋, 胡波. 一種超復(fù)數(shù)頻域的有意義數(shù)字水印算法[J]. 系統(tǒng)工程與電子技術(shù), 2009, 31(9): 2242-2248.
Jiang S H, Zhang J Q, and Hu B. Content based image watermarking algorithm in hypercomplex frequency domain[J].Systems Engineering and Electronics, 2009, 31(9):2242-2248.
[8]孫菁, 楊靜宇, 傅德勝. 彩色圖像四元數(shù)頻域幅值調(diào)制水印算法[J]. 計(jì)算機(jī)科學(xué), 2011, 38(3): 123-126, 139.
Sun J, Yang J Y, and Fu D S. Watermarking algorithm for color images based on quaternion frequency modulation[J].Computer Science, 2011, 38(3): 123-126, 139.
[9]Sangwine S J and Ell T A. Hypercomplex Fourier transforms of color images[J].IEEE Transactions on Image Processing,2007, 16(1): 22-35.
[10]Nicolas L B and Jerome M. Singular value decomposition of quaternion matrices: a new tool for vector-sensor signal processing[J].Signal Processing, 2004, 84(7): 1177-1182.
[11]Liu R Z and Tan T N. An SVD-based watermarking scheme for protecting rightful ownership[J].IEEE Transactions on Multimedia, 2002, 4(1): 121-128.
[12]Zhang X P and Li K. Comments on “an SVD-based watermarking scheme for protecting rightful ownership”[J].IEEE Transactions on Multimedia, 2005, 7(2): 593-594.
[13]Rykaczewski R. Comments on “an SVD-based watermarking scheme for protecting rightful ownership”[J].IEEE Transactions on Multimedia, 2007, 9(3): 421-423.
[14]Lai C C and Tsai C C. Digital image watermarking using discrete wavelet transform and singular value decomposition[J].IEEE Transactions on Instrumentation and Measurement,2010, 59(11): 3060-3063.

