用于多普勒流速剖面儀測波浪的方向譜反演算法研究

李 晨 吳建波 高 超 王道龍 李 俊 鄧 鍇 王長紅

①(中國科學院聲學研究所 北京 100190)

②(國家海洋局第一海洋研究所 青島 266003)

1 引言

海浪的方向譜給出海浪能量在頻率和方向上的2維分布，細致地描述了海浪能量的傳播信息。使用聲學多普勒流速剖面儀(Acoustic Doppler Current Profiler, ADCP)測波浪是目前精度較高、應用較廣的一種海浪測量手段，它利用各換能器空間位置不同造成的相位差來計算波向[1]。

ADCP測量波浪計算方向譜包括流速反演和波面高度反演兩種方法，其中波面高度反演由于直接測量波面變化，不需任何中間轉換，也無需考慮洋流影響[2]，而且水氣界面聲波反射強度明顯比水質點大，因此測量數據精確度較高，與雷達測波儀[3]相比測量精度與測量范圍均有一定優勢。

目前常見的幾種基于儀器陣列的海浪方向譜反演算法有最大似然法(MLM)、擴展本征矢(EEV)法和貝葉斯方向譜估計法(BDM)等。最大似然法是波浪方向譜分析中最常用的方法，具有計算速度快、計算結果穩定、對噪音不敏感等特點，同時具有一定的數值精度；但當儀器陣列距離反射面較近時，其方向分辨率會受到一定影響[4]。擴展本征矢法能夠得到能量分布更加集中于主波向的方向譜[5,6]，但其適用范圍有待進一步論證。貝葉斯法能夠使能量在方向上的分布更平滑，獲得更加可靠、精度更高的方向譜，前提是陣列元素個數不小于 4，交叉譜質量較好且儀器布放深度不宜過大[7]；其主要問題是計算時間長。美國RDI公司[1]和挪威Nortek公司[8]的ADCP波浪數據反演都使用了最大似然法。另外還有 SUV(Surface height, transverse velocity component(U)and longitudinal velocity component(V))法等，由于其只適用于含有中央垂向波束的情況[9]，因此本文暫未討論。

本文通過計算機仿真和實測數據處理兩方面工作，將目前常見的幾種基于儀器陣列的海浪方向譜反演算法用于4波束Janus配置的ADCP波面高度測量數據的處理并進行分析比較，確定它們在ADCP波浪方向譜反演中能夠取得的反演效果和適用范圍。本文選擇最具普遍性的 MLM、國內專家提出的EEV和國際公認精確度較高的BDM進行比較，具有典型意義；本文對3種算法進行了理論上的誤差分析與對比；在計算機仿真中，引入不同的儀器布放深度(影響波束投影位置、范圍與間距)作為變化因素進行理論分析和仿真結果的比較，使仿真更具實際意義；在實測數據處理中，一方面將RDI ADCP數據分別使用WavesMon軟件和我們自主編寫的算法進行反演并與比測儀器進行結果比較，另一方面將聲學所ADCP數據的反演結果與比測儀器進行比較，證明了我們自主研發的儀器和配套算法具有良好的波浪測量和反演精度。

2 算法原理

使用有限數據估計海浪方向譜的基本思想是，由同一物理量(波面高度或波生流速)在不同位置的時間序列(波束陣列，如ADCP情形)或者浪場中某一點處不同物理量的時間序列(定點測量，如浮標情形)經傅氏變換構成頻域交叉譜。波束陣列的交叉譜矩陣包含了同一頻率的波浪對于不同位置波束的相對相位信息，這正是方向譜反演的關鍵。

波束陣列的交叉譜與方向譜的關系可以表示為

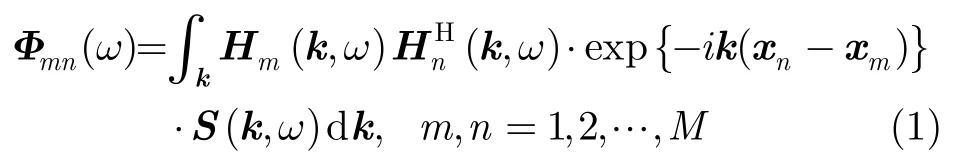
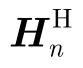
2.1 最大似然法

適用于波束陣列的最大似然法(Maximum Likelihood Method, MLM)基本思想是將方向譜估計值表示為交叉譜的線性疊加，并將此估計值最小化來接近真實值。方向譜估計值(k,ω)的表達式為

為了增加能量的集中程度，提高波向辨識度，在最大似然法中引入迭代。具體做法是用MLM算得的方向譜估計值0代入式(1)還原交叉譜，再用此交叉譜重新估計方向譜得到，最后通過

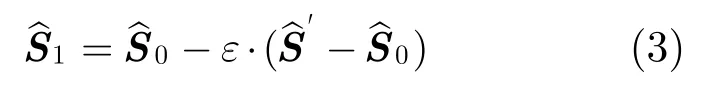
2.2 擴展本征矢法

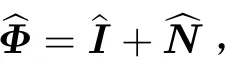
2.3 貝葉斯法

Hashimoto等人[7]將貝葉斯模型引入海浪方向譜的估計，稱其為貝葉斯方向譜估計法(Bayesian Directional spectrum estimation Method, BDM)，簡稱貝葉斯法?？紤]誤差ε，將交叉譜矩陣中的元素φi改寫為

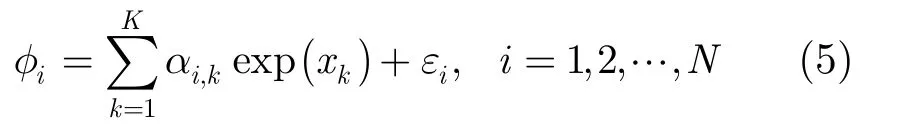
其中εi相互獨立，且遵從均值為 0、方差為σ2的高斯分布，N=M×M,K為方向離散點的個數。則最優的超參數u和方差σ2通過將赤池貝葉斯信息量標 準(Akaike’s Bayesian Information Criterion,ABIC)最小化求得

其中L(x,σ2)為給定φi時x和σ2的似然函數，p(x|u2,σ2)為x的先驗分布。

2.4 理論誤差分析

(1)在方向譜反演算法中，將頻率和方向分別進行離散化選點，所得方向譜實際上是由離散點數決定行(頻率)數和列(方向)數的2維矩陣。本文3種算法均采用逐行計算的方法，即依次對每個頻率離散點的方向分布進行解算；但在計算方向分布時，MLM和EEV對各個方向離散點的計算是孤立的，而BDM是通過解一個形如Ax=b的非齊次線性方程組來實現本頻率點的方向分布解算。顯然，在BDM的求解方法下，方向分布的相關性更強，隨機誤差的影響更小。

(2)為保證方向分布光滑連續，BDM 要求方向分布向量x(f)=[x1(f),x2(f), …,xK(f)]中的元素滿足xk-2xk-1+xk-2≈0,2＜k≤K；這一限定條件即包含在方程組Ax=b中。而MLM和EEV并無類似的平滑操作。

(3)BDM 計算x(f)是采用迭代法逐步逼近真實值，連續兩個x(f)的差向量的模值小于 10-3時迭代結束，以此計算ABIC，并通過改變超參數u的值重新計算x(f)，即在外層也建立迭代，選出最小的ABIC值和對應的x，從而降低誤差水平；如2.1節所述，MLM 也使用迭代對方向譜結果進行修正；而EEV并未引入修正算法。

(4)BDM 中非齊次線性方程組Ax=b求解x時，方程組有解的條件是增廣矩陣(A,b)的秩等于系數矩陣A的秩，而A是行數和列數均為K的方陣；顯然當K值較大時，方程組無解的可能性(即無法得到當前頻率點的方向分布)較大。這是BDM的一個顯著缺陷。

(5)EEV把交叉譜矩陣分成信號和噪聲兩部分，認為本征值明顯較大的部分為信號，其余為噪聲；MLM 則認為整個交叉譜矩陣均含有噪聲。顯然MLM的劃分方法更符合實際情況；而EEV將一部分噪聲也當作信號，這增加了信號部分的能量，使得方向譜反演結果的譜峰更加尖銳，但相對實際情況而言引入了人為誤差。

由上述分析可知，BDM采取的誤差消除措施最多，在方向分布有解的情況下，反演結果應最逼近真實值；MLM 進行了迭代計算，沒有平滑處理；EEV未引入修正和平滑算法，其結果誤差應為最大。BDM的缺陷是方向分布會有無解的情況發生，且由于其需要進行內外兩層迭代，因此運算耗時較長；而EEV具有譜峰尖銳的優勢。

3 計算機仿真

本文仿真和試驗采用的波浪觀測方法是，ADCP布放在海底，向上發射聲波波束，通過接收回波獲得水面高度變化的時間序列。

計算機仿真的步驟是：構造海面3維高度模型；根據儀器布放深度確定波束陣列水面投影的相對位置和范圍，采集投影內的水面高度數據；使用不同反演算法處理數據獲得方向譜結果。

3.1 海面模型

海浪不僅波高、頻率不盡相同，而且會沿各個方向傳播，除主波向以外，在其兩側±π/2范圍內都有諧波的擴散。根據線性海浪理論，可用雙疊加法模型(來源于Pierson模型)模擬3維波面[10]：

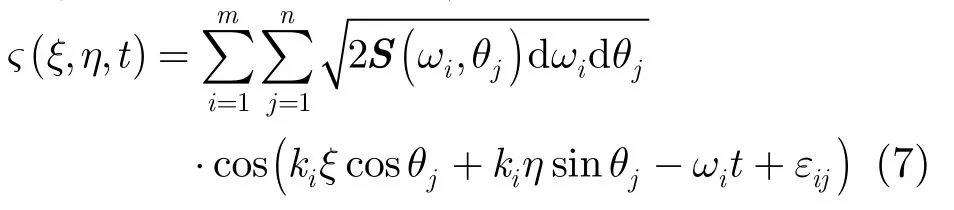
其中S(ωi,θj)為 2維海浪波譜，m,n分別為頻率和方向的離散化點數，ki為波數，ωi為角頻率，θj為方向角，ξ和η分別為海平面上各個離散點的橫坐標和縱坐標，εij為隨機初相位，是在0～2π間均勻分布的隨機變量。線性海浪理論應用于工程時，通常認為海浪能量的頻率分布和方向分布相互獨立，因此2維海浪譜可用1維海浪譜函數S(ω)和方向譜函數D(θ)的乘積來表示。

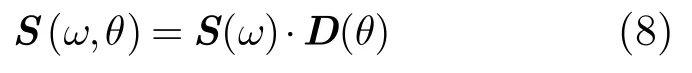
我們采用的1維海浪譜為 PM(Pierson-Moskowitz)譜，由于其數據基礎較為堅實，迄今仍是最常用的海浪頻譜模型之一。采用ISSC(國際船舶結構會議)建議的方向譜函數：

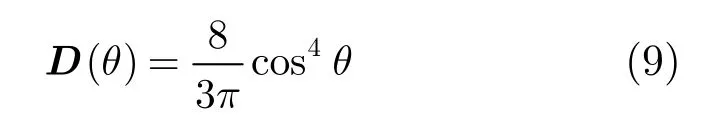
其中θ為組成波傳播方向相對風向的角度。

3.2 儀器布放

波束陣列測波浪根據各波束的相對位置和測得波浪的相對相位確定波長和波向等參數。當所測波浪的波長小于足印最小間距的2倍時，波束陣列將無法解出波向，這就是空間的奈奎斯特定理。在方向譜中，波長過小(或頻率過高)的波浪在正確波向以外的區域(即譜峰波向區域以外)會出現能量分布，這是波向解算錯誤在方向譜中的表現形式。而當各組成波的波長一定時，隨著足印間距的增加，能夠解出波向的波浪最小波長λmin隨之增加，方向譜反演結果中譜峰波向區域以外的能量分布范圍由高頻向低頻擴展，此區域能量幅值在頻率上的分布規律也與譜峰區域一致。這就是足印間距變化對方向譜能量分布造成的影響，在后面的仿真和實測結果圖中都得到了體現。

凹陷路面是典型的問題路面，一旦路面出現了因壓迫或是其他原因所產生的凹槽，便必然會出現承重問題。凹槽對于路基形成了一定程度上的破壞，路基的整體性能便會受到影響。所以不能只是簡單的對裂縫進行修補，而是要針對基層被損壞的部分去進行二次修建。要真正做好養護，必須要對路基的凹陷段以及翻漿的路段采取相應的治理措施去進行優化處理，在底層部分，需要使用水泥去對碎石砂（6%）開展墊層操作，穩定結構，并且要進行反復的進行碾壓，直到結構完全成型。在基層的修復結束后，可以利用再生瀝青對表層部分進行處理，這樣能夠得到更加理想的修復效果，盡可能避免凹陷問題的產生。

根據各算法的原理可知，足印間距只是式中的一個常數項，其值的改變并不會對算法本身引起的誤差造成影響；但由 2.4節可知，MLM, EEV和BDM對整體誤差的消除程度不同，因此由足印間距變化引起能量分布的變化對各算法的影響不同，各算法反演方向譜的譜峰區域和譜峰以外區域的能量分布都會存在差異。

本文仿真采用的ADCP波束陣列分布方式是經典的4波束Janus配置，波束的傾角θBeam=20°，波束開角θSensor=2°。如果令D為每個波束在水面投影(即“足印”)中心到整個波束陣列中心點的距離，則儀器的布放深度z與D的關系為D=z·tanθBeam。在每個以“足印”中心為圓心，半徑r=z·tanθSensor的水平圓面內采集波面高度數據，然后計算均值作為該測點當前時刻的水面高度測量值，因此儀器布放深度決定了各個波束投影的位置和間距。

由上面分析知，儀器布放深度與足印間距成正比，因此其與方向譜反演效果之間存在聯系，可通過改變其值對各種反演算法進行較全面的性能比較。布放深度z與足印最小間距Bmin的關系為

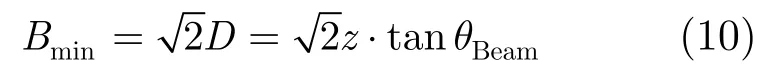
計算機仿真中的參數設置如表1所示，其中λ為所測波浪的譜峰波長。

表1 計算機仿真各參數設置

3.3 仿真結果

波浪方向譜以極坐標的形式表示，用顏色變化區分能量值的大小，單位為 m2/Hz/rad；為了便于比較，規定譜峰(即整個方向譜的能量最大值點)處能量為 1，以此將各方向譜進行能量歸一化，則所得譜圖即表示能量的分布情況和譜峰的尖銳程度。矢徑表示頻率，單位為Hz；極角表示方向，取值范圍為0～360°, 0°為正北，90°為正東，為符合日常觀察習慣，將坐標作了適當翻轉。

圖1為仿真數據的方向譜比較，圖2為仿真數據的能量在方向上1維分布比較。

圖1 仿真數據的方向譜比較，風速10 m/s

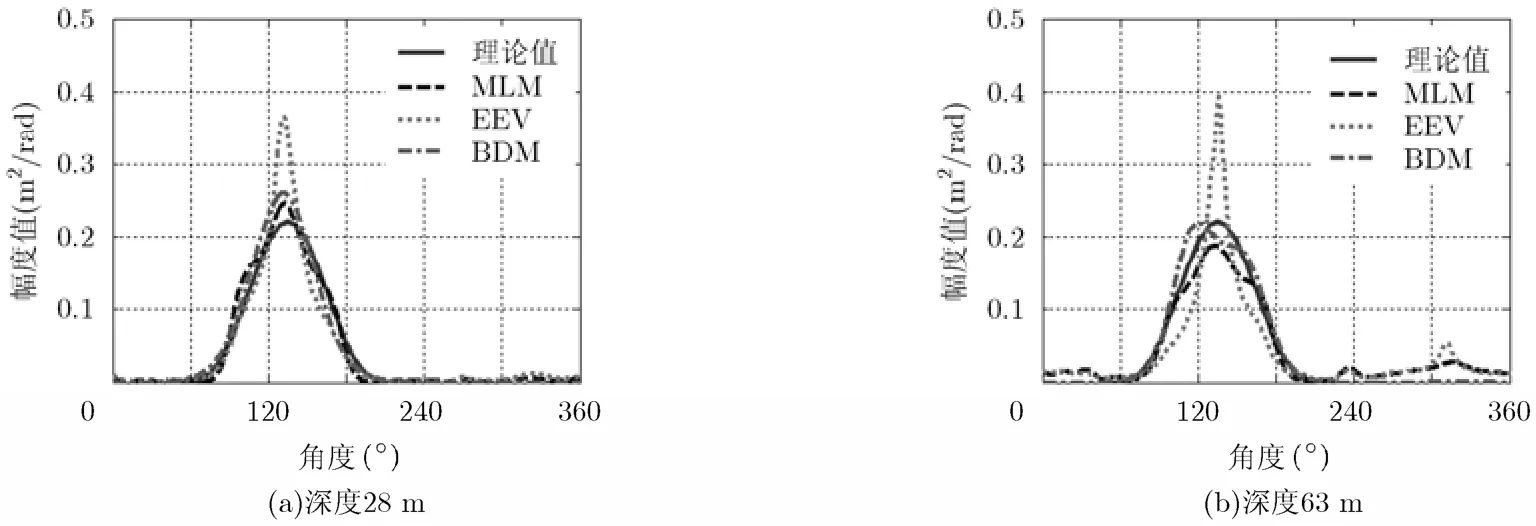
圖2 仿真數據的能量在方向上1維分布比較，風速10 m/s

3.4 結果分析

通過計算機仿真結果的比較可看出：

(2)EEV反演結果的譜峰最為尖銳，譜峰波向準確度最高；但峰值超出理論值較多，λ/2Bmin＜2時譜峰區域以外的能量分布較多。

(3)MLM 反演結果與理論能量分布的擬合度略差于BDM，但也能夠得到較為準確的譜峰區域和明確的譜峰波向，結果比較穩定；只是λ/2Bmin＜2時譜峰區域以外會出現較為明顯的能量分布。

4 實測數據處理

由于計算機仿真與實際情況之間必然會存在差異，因此為了考察各反演算法對于ADCP實測數據的適用性，我們分別使用RDI公司生產的600 kHz ADCP和中國科學院聲學研究所自行研制的 150 kHz ADCP工程樣機在青島近海進行波浪觀測試驗，通過分析其波面高度測量數據，對3種方向譜反演算法進行比較。儀器布放時考慮了空間的奈奎斯特定理，保證波束在水面投影的最小間距小于所測波浪波長的一半。兩臺儀器的換能器分布方式均為4波束Janus配置，波束的傾角為20°，波束開角為2°。

由于布放海域很難保證底部完全平坦，因此儀器實際測量時會產生布放偏差，即儀器布放傾斜導致各個波束在水面投影的相對位置出現偏移。為消除此誤差，在處理實測數據時，我們考慮儀器的實際姿態，根據兩個傾斜角縱搖(pitch)，橫搖(roll)計算各波束在水面的實際投影位置；只要保證各“足印”位置計算準確，其在一定程度內的相對位移變化(如縱搖，橫搖均在10°以內)就不會對反演結果的準確性產生影響。我們選擇波浪大小適宜、傾斜角較小的兩組實測數據進行分析比較，以保證其與計算機仿真結果具有對照意義。

試驗的海浪波長、儀器布放深度等參數如表 2所示，可見相對2011年1月5日的試驗條件而言，1月9日波浪的波長和λ/2Bmin的值都較大。

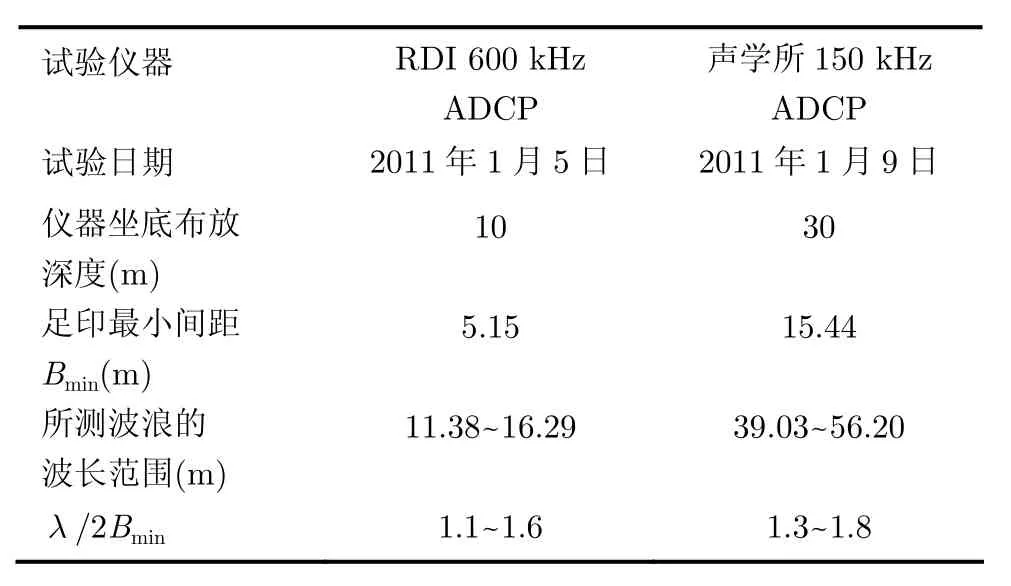
表2 試驗相關參數

由于本章方向譜的對比中使用了其他波浪數據處理軟件的截圖以及比測儀器反演結果的轉化圖，因此本章中的方向譜圖未進行統一尺度或能量歸一化操作，能量幅值的單位均為m2/Hz/rad。

4.1 ADCP實測數據反演結果

首先利用RDI公司的600 kHz ADCP測得的波浪高度數據，對3種方向譜反演算法進行比較。

因為 RDI有自己的波浪數據處理軟件 Waves Mon，所以我們可使用其反演結果作為比較標準；同時布放的還有 Datawell公司生產的波浪浮標(DWR MKIII波浪騎士)，由于其測量精度高，被稱為“測波的標準儀器”，因此也可使用其結果作為方向譜反演算法的性能衡量指標。結果如圖3所示。

其次利用中國科學院聲學研究所自行研制的150 kHz ADCP工程樣機測得的波浪高度數據，對3種方向譜反演算法進行比較。使用同時布放的波浪騎士的反演結果作為各算法的性能衡量指標。結果如圖4所示。

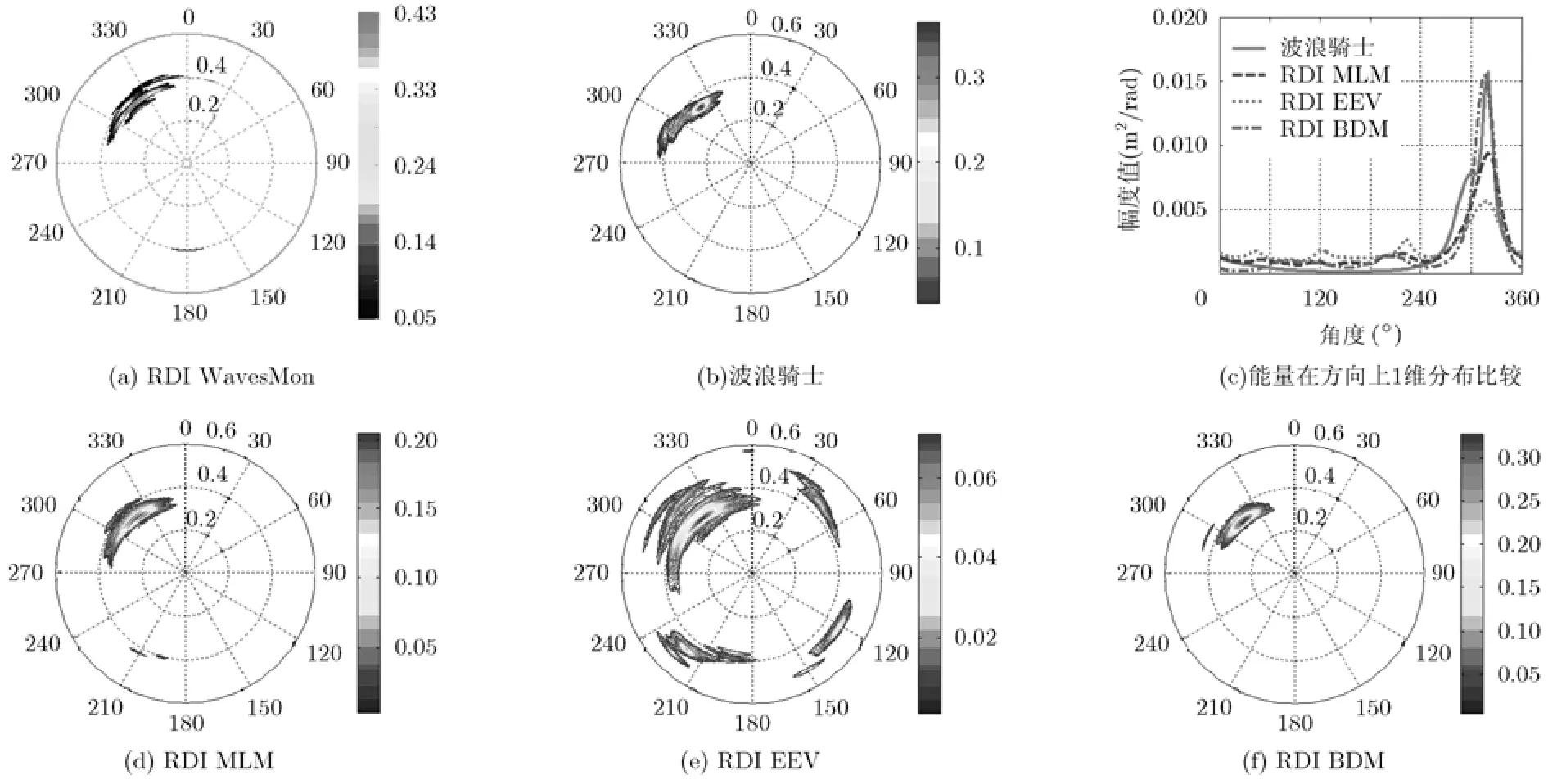
圖3 實測數據的方向譜和能量在方向上1維分布比較，2011年1月5日13:10

圖4 實測數據的方向譜和能量在方向上1維分布比較，2011年1月9日12:00

4.2 結果分析

綜合分析上述兩組實測結果可看出：

(1)實際測量中 BDM 仍能取得最佳的反演結果，能量分布最集中，譜峰區域以外的能量分布較少。但出現無解頻率點的現象仍會發生；其計算時間仍為MLM和EEV的數百倍。

(2)實際測量中 EEV 在λ/2Bmin較大的情況下體現出其譜峰較為尖銳的特性(但在能量在方向的1維分布中其譜峰尖銳程度與BDM相比略差)，且波向準確度較高。在λ/2Bmin較小的情況下其譜峰尖銳程度較差，能量分布最為分散，說明EEV的適用范圍小于BDM和MLM。

(3)MLM 的反演結果在波浪波長較小的情況下比BDM略差而明顯好于EEV，在波長較大的情況下與EEV相比各有優勢，因此在實測數據的反演計算中表現出較高的計算效率和穩定性。

5 結束語

綜上所述，通過MLM，EEV和BDM 3種波浪方向譜反演算法處理ADCP波面高度數據的結果對比，可以得出以下結論：

(1)根據計算機仿真和實測數據處理的結果得出的結論并不完全相同(如 EEV 方向譜的尖銳程度)，這是因為：一方面仿真模擬的是理想狀況，與實際海況相比存在差異，也說明現實海浪的復雜性；另一方面并未考慮聲波在傳播過程中的噪聲、散射等干擾因素對數據質量造成的影響。

(2)3種算法中，BDM能夠最為準確地再現波浪能量在方向上的分布，但由于其計算復雜度較高，因此會導致無解情況的發生(即對數據質量的要求較高)，而且計算時間遠遠大于另外兩種算法，即運算效率較低，因此適用于精度要求較高的計算。

(3)EEV能夠獲得明確尖銳的譜峰，波向準確度較高，但波浪波長偏小時反演結果相對較差，因此適用范圍比較有限，可在數據處理時作為參考。

(4)MLM 對計算機仿真數據和實測數據的反演都能夠取得令人較為滿意的結果，計算穩定度和效率最高，較適合應用于ADCP波面高度反演；其主要問題是譜峰區域以外會出現一定程度的能量分布，且要注意儀器布放時不能過分接近水面。

算法仍有改進的空間，如 BDM如何減少頻率點無解情況的發生；EEV如何擴大適用范圍；MLM如何減少譜峰區域以外的能量分布等。

[1]Brumley B H, Terray E A, and Strong B. System and method for measuring wave directional spectrum and wave height[P].US, Patent, No. 6052334, 2000.

[2]董兆乾, 蔣松年, 賀志剛. 南大洋船載走航式ADCP資料的技術處理和技術措施以及多學科應用[J]. 極地研究, 2010, 22(3):211-230.

Dong Zhao-qian, Jiang Song-nian, and He Zhi-gang. ADCP data technical processing of the CHINAREs and its multidisciplinary application[J].Chinese Journal of Polar Research, 2010, 22(3): 211-230.

[3]楚曉亮, 徐銘, 王峰, 等. 利用X波段雷達提取海浪信息的分析[J]. 中國海洋大學學報, 2011, 41(5): 110-113.

Chu Xiao-liang, Xu Ming, Wang Feng,et al.. Analysis of the wave information extracted by X band radar[J].Periodical of Ocean University of China, 2011, 41(5): 110-113.

[4]Isobe M and Kondo K. Method for estimating directional wave spectrum in incident and reflected wave field[C]. 19th International Conference on Coastal Engineering, Houston,TX, Sept. 1984: 467-483.

[5]管長龍, 文圣常, 張大錯. 分析海浪方向譜的擴展本征矢方法I: 方法的導出[J]. 海洋與湖沼, 1995, 26(1): 58-62.

Guan Chang-long, Wen Sheng-chang, and Zhang Da-cuo. An extended eigenvector method for estimation of directional spectra of sea waves I: derivation of the method[J].Oceanologia et Limnologia Sinica, 1995, 26(1): 58-62.

[6]管長龍, 文圣常, 張大錯. 分析海浪方向譜的擴展本征矢方法II: 方法的驗證、比較和應用[J]. 海洋與湖沼, 1995, 26(3):241-246.

Guan Chang-long, Wen Sheng-chang, and Zhang Da-cuo. An extended eigenvector method for estimation of directional spectra of sea waves II: verification, comparison and application of the method[J].Oceanologia et Limnologia Sinica, 1995, 26(3): 241-246.

[7]Hashimoto N and Kobune K. Directional spectrum estimation from a Bayesian approach[C]. 21st International Conference on Coastal Engineering, Coata del Sol-Malaga,Spain, June 1988: 62-76.

[8]Siegel E, Pedersen T, and Maatje J. Real-time directional wave measurements: innovative engineering for subsurface acoustic Doppler current profilers[EB/OL]. http://www.nortekusa.com/lib/technical-notes/awac-introduction-in-sea-technology-february-2006, Feb. 2006.

[9]李亞光, 吳建波, 高超, 等. 基于 AWAC型 ADCP的波浪反演算法研究[J]. 海洋技術, 2010, 29(3): 55-58.

Li Ya-guang, Wu Jian-bo, Gao Chao,et al.. Research on wave direction measurement using AWAC ADCP[J].Ocean Technology, 2010, 29(3): 55-58.

[10]文圣常, 余宙文. 海浪理論與計算原理[M]. 北京: 科學出版社, 1984: 127-130, 276-278.

Wen Sheng-chang and Yu Zhou-wen. Ocean Theory and Computing Principles[M]. Beijing: Science Press, 1984:127-130, 276-278.