基于偽布爾可滿足性的納米CMOS電路單元配置

王先建 王倫耀 儲著飛 夏銀水

(寧波大學信息科學與工程學院 寧波 315211)

1 引言

CMOL電路是結合納米技術和傳統 CMOS工藝的 CMOS/納米線/分子混合(CMOS/nanowire/MOLecular hybrid, CMOL)電路結構[1]，而且文獻[2]從理論上證明了 CMOL電路進行單元配置可實現電路邏輯功能的完備性。由于CMOL電路結構既保留了目前成熟的CMOS工藝，同時又具有納電子器件所具有的高密度特點而受到研究者們的廣泛關注，其研究內容包括 CMOL存儲器[3]、CMOL FPGA[4]以及神經元電路[5]等等。而在有關 CMOL CAD的研究中，CMOL的單元配置方法一直是一個重要內容[4,6-8]，因為它是 CMOL電路實現特定功能必經的步驟。

目前對 CMOL電路的單元配置方法已經開展了一些研究。這些方法包括基于邏輯簇(Tile)的設計方法[4]，基于力矢量算法[6]，啟發式算法[7]以及電路等效變換法[8]等，并發展出了CMOL自動綜合工具CMOL FPGA CAD 1.0[4]。

CMOL電路的單元配置問題實際上也可以被描述成一個可滿足性問題(Satisfiability Problem)，因此可以利用布爾可滿足性(Boolean Satisfiability,SAT)來解決 CMOL電路的單元配置問題。但在已發表的利用SAT實現CMOL電路單元配置的方法中[9]，由于采用二項式編碼[10]，使得子句的個數過多、中間處理文件過大，影響了算法的效率和處理電路大小的能力。相比于用合取范式(Conjunctive Normal Form, CNF)表示的約束，偽布爾(Pseudo-Boolean, PB)約束更加容易表示[11-15]。目前偽布爾可滿足性(Pseudo-Boolean Satisfiability, PBS)法[11]已被成功應用于低功耗狀態分配[12]和最大電路開關性估計[13]等領域中。本文提出利用 PBS法來解決CMOL電路的單元配置問題，該方法在不增加額外的布爾變量集個數的條件下，通過降低編碼過程中的約束個數[10,11]達到減少中間處理文件大小的目的。實驗結果表明，相比于文獻[9]的基于傳統SAT的CMOL單元配置方法，本文采用的方法能有效減少中間處理文件大小，達到加快算法速度和提高求解電路規模的目的。

2 CMOL FPGA結構

在CMOL電路中，納米線以一定的長度周期性斷開，納米線的這種特點使得每一個CMOL單元只能與周圍M=2r(r-1)-1個其它 CMOL單元相連，其中r為連通域半徑。以圖1為例，其中r為3，圖中深灰色單元C只能與周圍 11個淺灰色單元連通，這些淺灰色單元構成了深灰色單元的連通域。此外，CMOL電路中的兩點相對位置常用曼哈頓距離來表示。如在圖1中，C,D兩個CMOL單元的坐標分別為C(x1,y1),D(x2,y2)，則它們之間的曼哈頓距離為|x1-x2|+|y1-y2|。利用連通域半徑和曼哈頓距離就可以確定某一CMOL單元的連通域。以圖1為例，在圖1中坐標原點在C上，坐標軸將圖1分為4塊，分別為第1至第4象限，則當圖1中某一點D與C的曼哈頓距離分別不大于r,r-1,r-2 及r-1時，那么滿足這些曼哈頓距離約束條件的CMOL單元D的個數就是CMOL單元C的連通域大小。

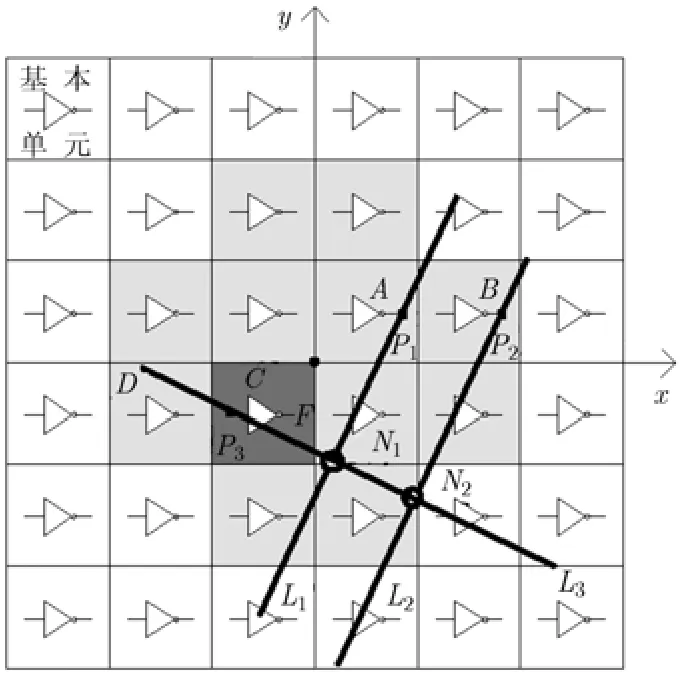
圖1 CMOL FPGA

3 CMOL單元配置問題的PBS描述

3.1 偽布爾可滿足性

SAT是用來解決給定的布爾方程是否存在一組變量賦值使問題為可滿足。而布爾方程的描述常采用CNF來表示。在CNF中，由m個子句w1,…,wm的合取組成；而子句由k個文字的析取組成。其中一個文字即為一個變量或者其反變量。因此，為了滿足一個式子，每一個子句必須至少有一個文字的值為真。

隨著SAT法的快速發展，SAT求解器被擴展用來處理PB約束，即為帶整數系數的線性不等式。偽布爾可滿足性問題可表示為 PB約束的合取，其中PB約束可表示為

式(1)中ai和b為整數常數；li為一個文字，可表示為變量xi和其反變量，即li=xi或者li=，其中xi∈{0,1},；“?”為關系操作符，可表示“=”，“＞”，“≥”，“＜”或者“≤”。若式(1)中的|ai|都為同一個數a0時，則式(1)對應的 PB約束稱為基數約束(cardinality constraints)，即

假設一個PB式子F為PB約束的合取。對于PBS問題，如果存在一組配置解x1,…,xm滿足所有的PB約束使得F為真，則表示F可滿足，這一組解即為可配置解。

例如，給定一個F(x1,x2,x3)=(2x1-2x2≥1)∧(x1+x2+3≥1)，它由3個布爾變量，5個文字，2個 PB約束組成。{x1=1,x2=0,x3=1}和{x1=1,x2=0,x3=0}等都為可滿足配置解。

3.2 CMOL單元配置問題的PBS描述

由于CMOL電路僅適于“或非/非”邏輯電路，因此在進行 CMOL單元配置之前需要對原始電路進行轉換，該轉換可以借助邏輯綜合工具SIS將由“與/或/非”邏輯電路轉換成“或非/非”邏輯電路。而 CMOL單元配置過程就是通過設置可配置納米二極管的狀態，將一個給定的邏輯電路功能用CMOL FPGA實現的過程。

在CMOL單元配置過程中，一般將電路輸入輸出端口放在CMOL電路的四周。因此對于一個由行(row)，列(column)構成的CMOL單元陣列，令C表示該陣列的CMOL單元集合，||C||表示集合C中的元素個數；C1表示位于C邊界上的 CMOL單元集合，||C1||表示集合C1中的元素個數；C2表示位于非C邊界上的CMOL單元集合，||C2||表示集合C2中的元素個數。則有

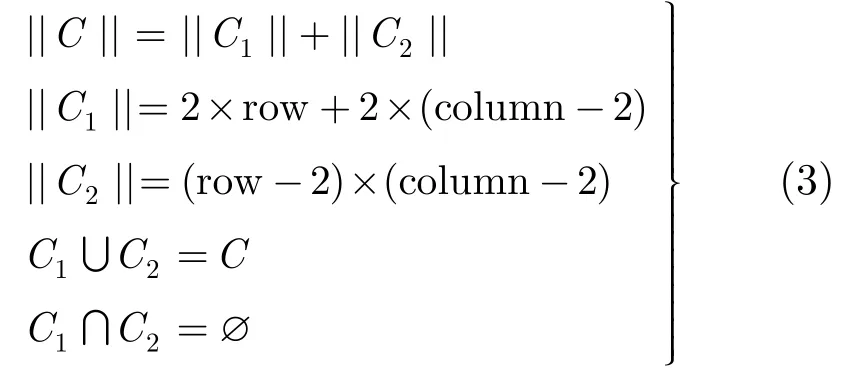
由于CMOL電路結構存在連通域約束，因此對于一個CMOL單元c,c∈C,D(c)為構成c的連通域的CMOL單元的集合，則有

給定一個基于“或非/非”邏輯的電路K，電路K可被看作是一個無環有向圖(Directed Acyclic Graph, DAG)，即K=(G,E)。其中G為對應于“或非/非”門的節點集合，E=G×G表示連接的門與門的邊的集合。對于電路中的任意門g,g'∈G，要想得到(g,g')∈E，當且僅當門g的輸出與門g'的輸入相連，亦即

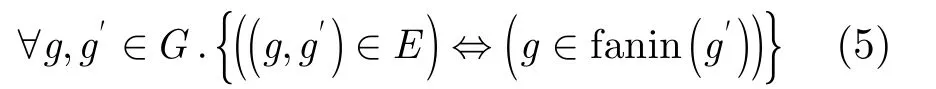
根據邏輯門在邏輯電路中所處的位置的不同，可以將邏輯門集合G分為3個子集，即G1,G2和G3，分別表示輸入端口的邏輯門集合，輸出端口的邏輯門集合和非輸入輸出端口的邏輯門集合，并用||G1||,||G2||和||G3||表示各子集中包含的元素個數。并且有

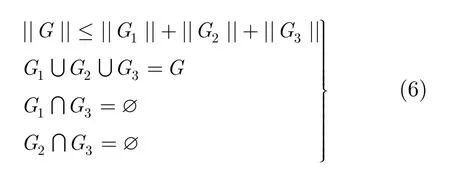
CMOL單元配置問題則可描述為將給定的電路邏輯門的集合G配置到 CMOL單元集合C中是否存在可配置解的問題。CMOL單元配置問題可用數學式描述成一個內射函數P，即P:G→C。在進行CMOL單元配置過程中，至少要滿足以下4個約束：

(1)與輸入、輸出端口相連的門必須被配置到陣列邊界的CMOL單元上，作為I/O口，即

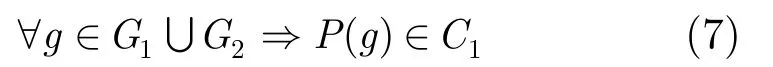
(2)每個“或非/非”門必須被配置到有且僅有一個CMOL單元上，即

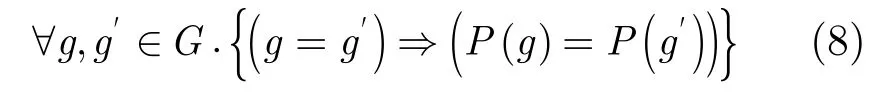
(3)兩個或者兩個以上不同的門不能被配置到同一個CMOL單元上，即

(4)電路中有連接關系的門單元位于各自的連通域中，即

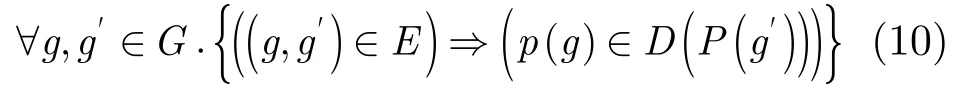
考慮到 CNF中子句的數量與布爾變量成指數級增加，為此本文在不增加額外的布爾變量集個數的條件下，采用PB約束代替CNF，達到減少約束個數的目的。在描述CMOL單元配置問題時，ai為0或1,b為 1，相關的PB約束可以表示為以下 3種約束，分別為：

(1)關系操作符“?”為“≤”時，即為“至多一個”基數約束，簡稱AMO(At-Most-One)約束，即

(2)關系操作符“?”為“≥”時，即為“至少一個”基數約束，簡稱ALO(At-Least-One)約束。這種PB約束等價于標準的SAT子句，即

(3)關系操作符“?”為“=”時，即為“有且僅有一個”基數約束，簡稱EO(Exactly-One)約束，即

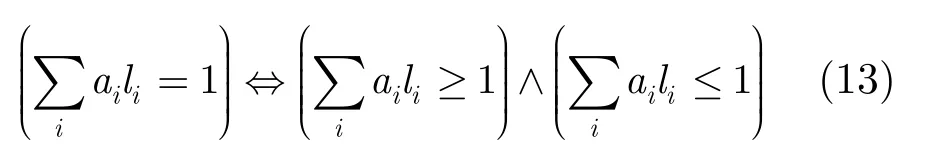
CMOL單元配置問題主要由這3種基數約束來表示，從3種基數約束可以看出，只須對AMO約束進行改進即可。傳統的SAT法針對AMO約束采用二項式編碼法，即

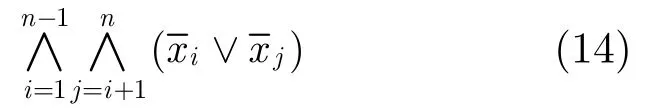
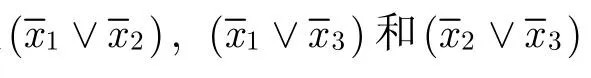
在本文中，布爾變量表示將門g配置到CMOL單元c中，其中g∈G和c∈C。因此給定一個電路G和CMOL單元陣列，符合式(7)-式(10)的CMOL單元配置可以被編碼成以下幾種類型的PB約束：

(1)當門g必須被配置到有且僅有一個 CMOL單元c上，即可編碼成

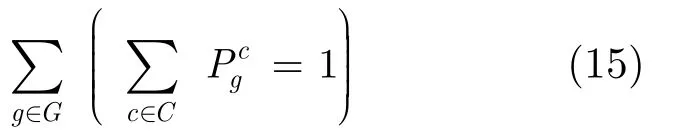
(2)當CMOL單元c至多被一個門g配置，即可編碼成

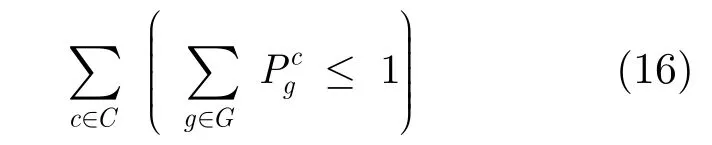
(3)當門g'配置在CMOL單元c上，那么與門g'的輸入線有連接關系的門g應該配置在CMOL單元c的連通域范圍內，即可編碼成

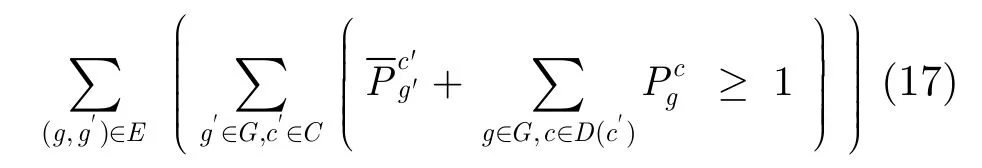
將式(15)-式(17)中的PB約束集導入PBS求解器中。針對CMOL單元配置時碰到的實際問題，可導入更多其它的PB約束。例如，任意的“或非/非”門可以配置到滿足以上 PB約束的任意的CMOL單元上。考慮到屬于G1和G2的門被要求配置在陣列邊界當作I/O口，因此可設置 Σc∈C1=1。這樣能夠通過PB約束傳播達到簡化CMOL單元配置問題。

PBS法的具體步驟為：

步驟 1 通過 SIS邏輯綜合工具將原始 BLIF電路網表文件轉換成全由“或非/非”門組成的BLIF格式電路文件；

步驟 2 讀入基于“或非/非”門的BLIF電路，對輸入信號、“或非/非”門等進行標號；

步驟 3 根據標號的個數以及I/O個數來設置CMOL單元陣列大小；

步驟 4 應用PBS法根據式(7)-式(10)的條件約束將基于“或非/非”門的 BLIF電路配置到CMOL單元陣列中；

步驟 5 將步驟 4中的所有 PB約束導入到PBS求解器中，如果有一個解滿足所有的PB約束，那這個解就是CMOL單元配置解，反之則無可配置解。

4 實例說明

下面以全加器為例子來說明一個原始的電路是如何利用PBS法配置到CMOL電路中的。

步驟 1 通過 SIS邏輯綜合工具對原始全加器的BLIF電路網表文件轉換成由“或非/非”門組成的BLIF格式電路文件，如圖2(a)所示。

步驟 2 由圖 2(a)中可以看出，電路有 3個輸入信號A,B,C, 2個輸出信號Sum,D，有 15個標號，其中標號1, 2, 3為輸入信號，標號11, 15為輸出信號門，標號4, 5, 6為“非”門，標號7, 8,9, 10, 11, 12, 13, 14, 15為“或非”門。并將它們之間的連接關系進行記錄，例如標號 11的門與標號7, 8, 9, 10的門相連。

步驟 3 此例可設置5×4大小的 CMOL單元陣列，如圖2(b)所示。為與傳統的SAT法進行公平對比，默認設置連通域半徑r也為9。

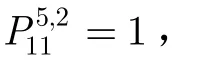
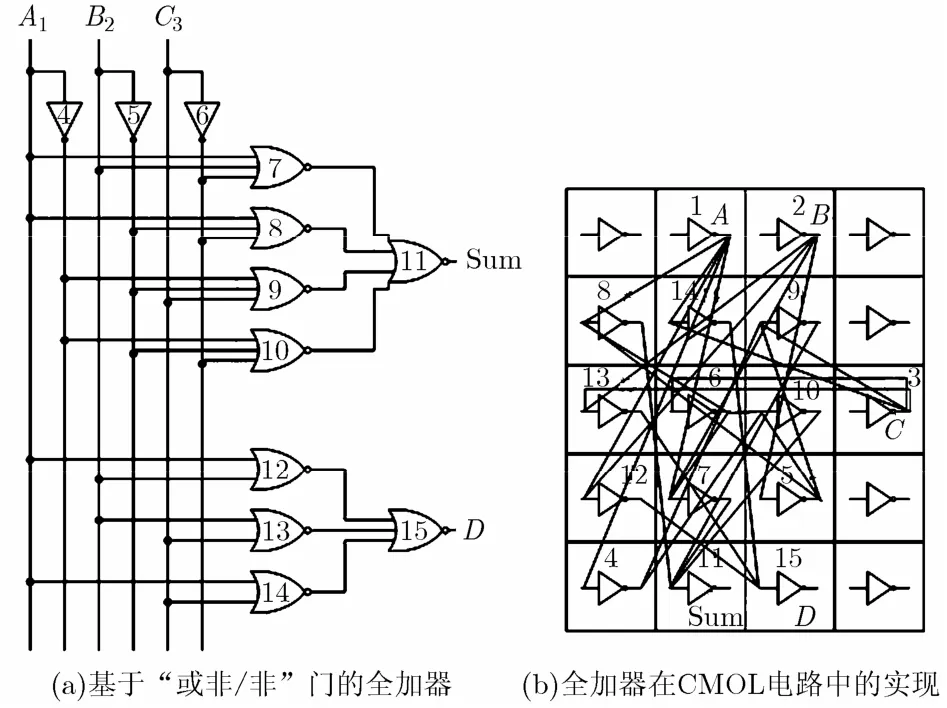
圖2 全加器實例

步驟5 將步驟4中的所有PB約束導入到PBS求解器中，如果有一個解滿足所有的PB約束，那這個解就是CMOL單元配置解。即基于“或非/非”門的全加器電路成功配置到CMOL電路中。

5 實驗結果

本文中提到的基于PBS的CMOL單元配置法用C語言編程實現，通過GCC編譯，在linux操作系統及Intel Pentium Dual-core 3 GHz CPU, 2 GBRAM的PC環境下運行。表1中的數據是采用perl腳本語言對每個測試電路進行20次的實驗測試，然后取出相對公平的中間值得到的。

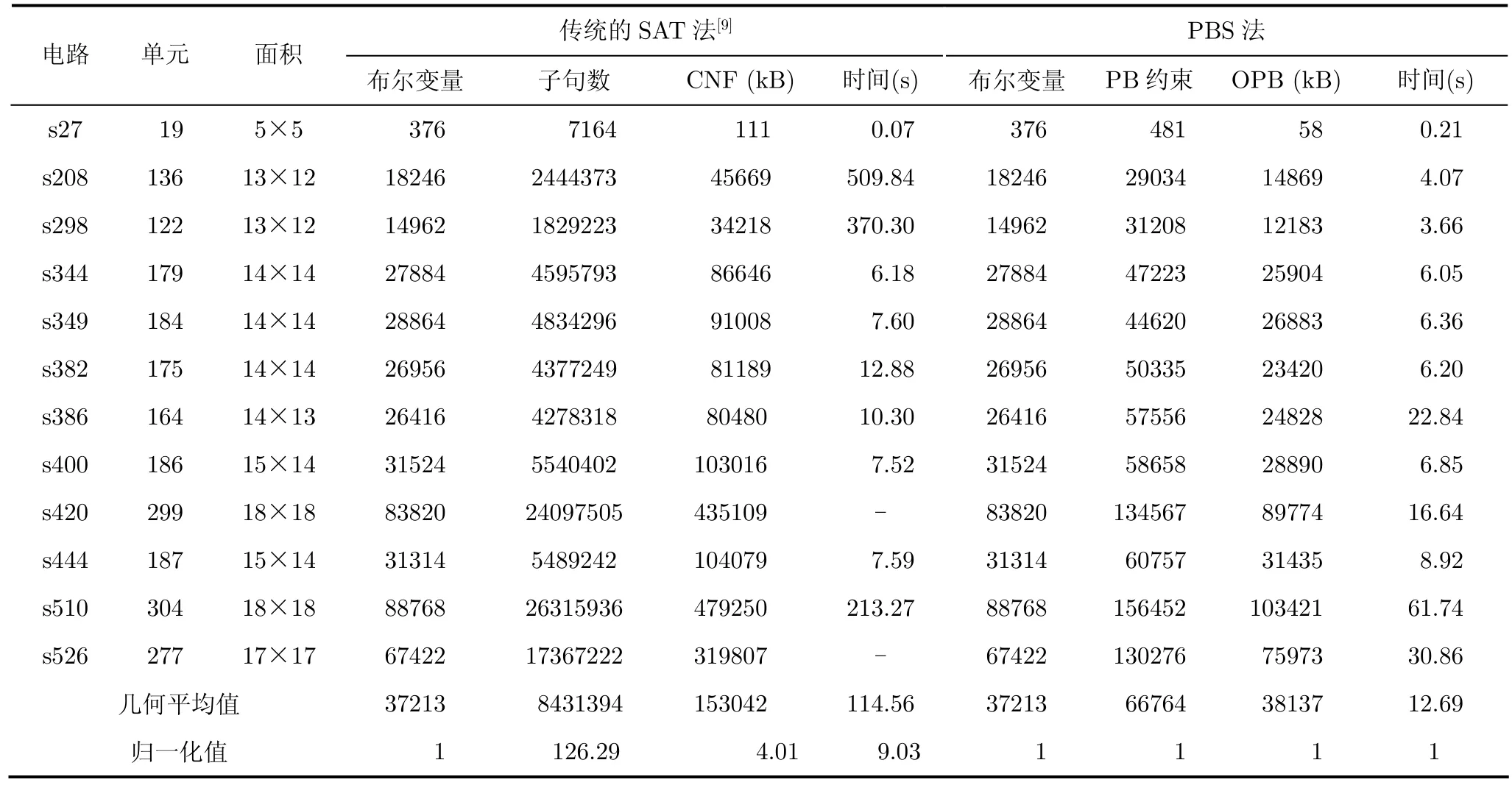
表1 實驗結果

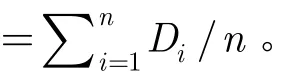
從表1可以看出，相對于傳統的SAT法，PBS法在沒有增加額外的布爾變量集個數的基礎上，SAT法中的子句個數平均為PBS法中的PB約束個數的126.29倍，說明PBS法比傳統的SAT法更易表示、更簡單。CNF大小平均為OPB大小的4.01倍。考慮到OPB文件為PB約束的合取，亦即單元配置過程中產生的中間處理文件，它的減小有利于CAD工具在運行過程中占用更少的內存，或可求解更大的電路。從時間來看，對于 s27, s386及 s444 3個電路，PBS法所用時間稍微比傳統的SAT法略長一點，但從平均值角度看，PBS法求解速度要比傳統的SAT法求解速度快9.03倍。并且傳統的SAT法對于s420及s526兩個電路無法求解，而PBS法可以。

6 結論

針對 CMOL單元配置問題，本文提出了基于PBS的單元配置方法。傳統的SAT法在處理CMOL單元配置過程中，因采用二項式編碼使得子句的個數過多、中間處理文件過大，影響了算法的效率和處理電路大小的能力。為此，本文在不增加額外的布爾變量集個數的條件下，通過降低約束個數、減小中間處理文件，將問題編碼成PBS問題。實驗結果表明，PBS法的PB約束個數比傳統的SAT法的子句個數平均減少了126.29倍，中間處理文件大小平均減少了4.01倍，CPU運行時間平均快了9.03倍，并且增大了求解規模。

[1]Likharev K K and Strukov D B. CMOL: Devices, Circuits,and Architectures. Introducing Molecular Electronics[M].Berlin: Springer, 2005: 447-477.

[2]Chen Gang, Song Xiao-yu, and Hu Ping. A theoretical investigation on CMOL FPGA cell assignment problem[J].IEEE Transactions on Nanotechnology, 2009, 8(3): 322-329.

[3]Strukov D B and Likharev K K. Defect-tolerant architectures for nanoelectronic crossbar memories[J].Journal of Nanoscience and Nanotechnology, 2007, 7(1): 151-167.

[4]Strukov D B and Likharev K K. CMOL FPGA circuits[C].Proceedings of International Conference on Computer Design,Las Vegas, Nevada, USA, June 26-29, 2006: 213-219.

[5]Afifi A, Ayatollahi A, and Raissi F. CMOL implementation of spiking neurons and spike-timing dependent plasticity[J].International Journal of Circuit Theory and Applications,2011, 39(4): 357-372.

[6]Kim K, Karri R, and Orailoglu A. Design automation for hybrid CMOS-nanoelectronics crossbars[C]. Proceedings of IEEE International Symposium on Nanoscale Architectures,Los Alamitos, CA, USA, October 21-22, 2007: 27-32.

[7]Xia Yin-shui, Chu Zhu-fei, and Hung N N,et al.. An intergrate optimizaiton approach for nano-hybrid circuit cell mapping[J].IEEE Transactions on Nanotechnology, 2011,10(6): 1275-1284.

[8]夏銀水, 儲著飛, 王倫耀, 等. 納米CMOS電路邏輯等效轉換[J]. 電子與信息學報, 2011, 33(7): 1733-1737.

Xia Yin-shui, Chu Zhu-fei, and Wang Lun-yao,et al.. Logic equivalent transformation for nano-meter CMOS hybrid circuits[J].Jounal of Electronics&Information Technology,2011, 33(7): 1733-1737.

[9]Hung N N, Gao Chang-jian, and Song Xiao-yu,et al.. Defect tolerant CMOL cell assignment via satisfiability[J].IEEE Sensors Journal, 2008, 8(6): 823-830.

[10]Chen Jing-chao. A new SAT encoding of the at-most-one constraint[C]. Proceedings of the Tenth International Workshop on Constraint Modelling and Reformulating, St.Andrews, Scotland, UK, September 6, 2010.

[11]Roussel O and Manquinho V. Pseudo-Boolean and Cardinality Constraints. Handbook of Satisfibility[M].Amsterdam: IOS Press, 2009: 695-733.

[12]Sagahyroon A, Aloul F, and Sudnitson A. Using SAT-based techniques in low power state assignment[J].Journal of Circuits,Systems,and Computers, 2011, 20(8): 1-14.

[13]Mangassarian H, Veneris A, and Najm F N. Maximum circuit activity estimation using Pseudo-Boolean Satisfiability[J].IEEE Transactions on Computer-Aided Design of Intergrated Circuits and Systems, 2012, 31(2): 271-284.

[14]Eén N and S?rensson N. Translating Pseudo-Boolean constraints into SAT[J].Journal of Satisfiability,Boolean Modeling and Computation, 2006, 2: 1-26.

[15]Berre D Le and Parrain A. The Sat4j library, release 2.2 system description[J].Journal on Satisfiability,Boolean Modeling and Computation, 2010, 7: 59-64.