基于貝葉斯信息準則的極化干涉SAR圖像非監督分類

楊 文 顏 衛 涂尚坦 廖明生

①(武漢大學電子信息學院 武漢 430072)

②(武漢大學測繪遙感信息工程國家重點實驗室 武漢 430079)

1 引言

極化干涉合成孔徑雷達(Polarimetric Interferometry SAR, PolInSAR)是利用極化合成孔徑雷達進行干涉測量的新型成像雷達。極化干涉合成孔徑雷達通過極化信息和干涉信息的融合，有效地擴展了觀測空間。極化干涉SAR不僅具有對目標散射體的精細物理形狀敏感的特性，而且包含目標散射體空間分布的信息，大大提高了對地物的識別能力[1]。

非監督分類是極化干涉 SAR圖像自動解譯中最為基本和重要的應用之一，也是研究的熱點領域。目前已有多種極化干涉 SAR非監督分類方法被提出來。2001年，文獻[2]給出了利用L波段的E-SAR極化干涉SAR數據進行地物分類的精細分析，通過利用極化干涉熵和極化干涉各向異性度特征，有效地改善了初始分類的效果。2004年，文獻[3]也利用極化干涉熵和極化干涉各向異性度進行極化干涉SAR非監督分類研究。2005年，文獻[4]基于極化干涉 SAR數據相干系數在單位復數橢圓中的分布形狀，并利用得到的橢圓率等參數對極化干涉SAR圖像進行分類。文獻[5]利用Shannon熵特征的強度，極化度和干涉3個分量，進行地物分類，獲得了好的效果。文獻[6,7]利用Shannon熵分解的強度，極化度和干涉度 3個貢獻度來均等地利用極化干涉SAR數據強度，極化和干涉信息。實驗結果表明了利用Shannon熵特征進行地物分類的有效性。

圖像的非監督分類問題，本質上是判定哪些像素和哪些像素應該被分在一類中，也就是應該把哪些像素聚成一類，其中涉及到了每個像素類別標號的確定和聚類類數的確定[8]。在前文所提到的極化干涉SAR圖像非監督分類算法中，主要側重于研究如何更加準確地進行每個像素的標號確定，而對如何確定聚類類別數的研究較少。2007年，文獻[9]利用自啟動的方式來進行極化干涉 SAR數據非監督分類，同時利用極化干涉SAR中干涉相位差來自動確定類別數，獲得了比較好的實驗效果。但文獻中只利用了部分極化干涉SAR數據信息來確定類別數，存在一定的偏差。同年，文獻[10]利用對數似然函數作為判定準則，采用交叉驗證的方式，在極化SAR圖像非監督分類中確定最佳類別數。文獻中利用對數似然函數的拐點來判斷類別數，需要進行人工判定，存在一定的人為誤差。

本文針對極化干涉 SAR圖像非監督分類最佳類別數確定的問題，提出了在Wishart統計模型下，基于貝葉斯信息準則來自動確定最佳類別數的方法。為了提高極化干涉SAR非監督分類標號確定的準確性，本文利用Shannon熵分解特征中的強度，極化度和干涉3個分量對地物進行初始分類，然后利用期望最大化(Expectation-Maximization, EM)和標號代價(LabelCost)優化[11]算法對分類結果進行迭代優化，以獲得穩定的分類結果。最后利用德國航空航天中心(German Aerospace Center, DLR)E-SAR機載SAR德國Oberpfaffenhofen 地區的極化干涉SAR數據和中國電子科技集團第38研究所(CETC 38)的機載 SAR海南陵水地區極化干涉SAR數據驗證了算法的有效性。

2 Shannon熵特征

在極化干涉SAR數據的基礎數學模型中，回波信號被定義成一個6維向量的形式，以表現兩根天線不同極化通道的反射強度。

其中h,v表示不同方向的發射波。

極化干涉SAR協方差矩陣滿足Wishart分布，其定義如下：

其中Γi為天線的極化協方差矩陣，包含了對應天線的極化信息。Ω12表示天線間的相干性，包含了兩天線的干涉信息。

在標準的極化干涉SAR數據模型中，Shannon熵表示式如式(3)所示[12]。

極化干涉SAR數據的Shannon熵分解如下：

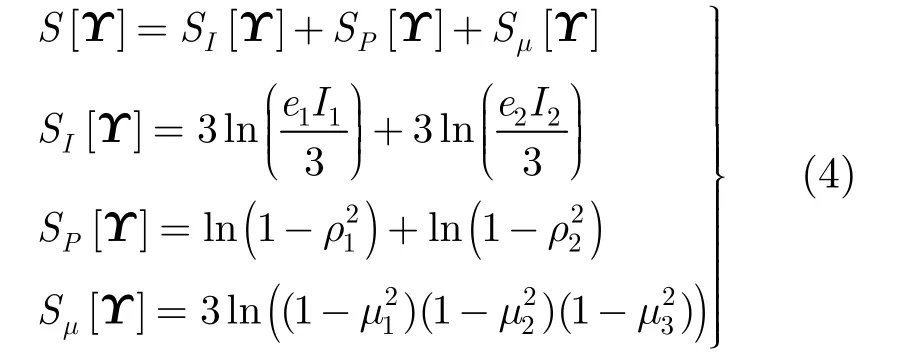
3 貝葉斯信息準則

圖像的非監督分類問題，涉及到像素標號的確定和圖像類別數確定的問題。傳統的聚類算法，如Kmeans, EM等，聚類數目K需要預先根據經驗給定。而聚類數目的不同，直接影響到分類結果的好壞。貝葉斯信息準則(Bayesian Information Criterion, BIC)是確定類別數目的常用方法，其定義如下：

其中Lk(X)是模型f(·|)在樣本集X上的對數似然函數，是對模型復雜性(模型參數數目)的懲罰項。似然函數可以理解為條件概率的逆反，為了便于分析取對數變換，對數似然函數定義如下：

其中Θk為每一類的模型參數，xl為測試樣本數據。對于極化干涉SAR圖像非監督分類問題，一般利用極化干涉 SAR數據協方差矩陣進行分類。基于復Wishart分布可以得到

因此，基于復Wishart分布的BIC準則定義如下：

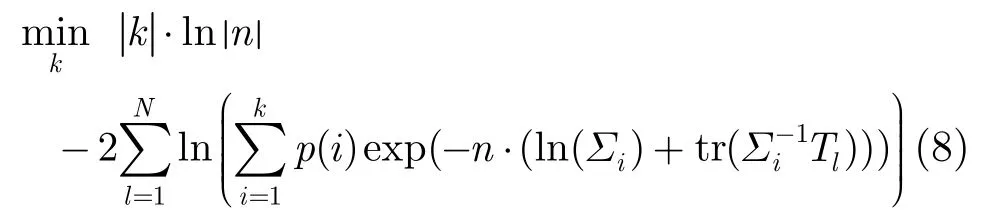
根據BIC準則，在同時考慮似然項和懲罰項的同時，通過尋找似然函數與類別數的變化曲線的最小值得到最佳類別數。

4 LabelCost能量優化

傳統的迭代聚類算法都假定像素點之間是相互獨立的，尤其是在SAR數據中，SAR圖像中相干斑噪聲干擾比較嚴重。為了抑制相干斑噪聲對分類結果的影響，一般通過建立馬爾科夫隨機場(Markov Random Field, MRF)，利用平滑先驗信息，來提高分類精度和分類結果的可視性。

LabelCost算法，是Delong等人[13]最近提出的能量優化算法，其同時考慮了數據項，平滑代價項和標號代價項，從而將能量函數描述為3項之和，提高了算法的準確度與適用性，其能量函數表示如式(9)：

其中，第1項為傳統的數據代價項，表示觀測數據信息對分類標號推理的勢能，第2項為平滑代價項，主要考慮平滑先驗信息的勢能。第3項為標號代價項，主要考慮標號代價的勢能。本文，基于EM迭代框架，利用LabelCost能量優化算法，通過引入平滑代價項和標號代價項，抑制相干斑噪聲對分類結果的影響，從而有效的提高了非監督分類的精度。

5 算法具體流程

在本文中，分類算法首先利用Shannon熵特征進行初始分類，并利用EM算法和LabelCost算法進行迭代優化，獲得穩定的聚類結果。同時利用BIC準則確定最佳類別數，從而獲得在最佳類別數下的穩定的分類結果。算法具體的流程如圖1所示，具體步驟如下：

圖1 自動確定類別數的極化干涉SAR非監督分類流程

(1)從極化干涉 SAR協方差矩陣數據提取對應的Shannon熵特征，然后基于Shannon熵特征分解，得到強度，極化度和干涉度3個分量。

(2)根據強度，極化度和干涉度能量大小進行初始化分類。按照每種能量大小分別把圖像分割成 3類，以有效利用極化干涉SAR數據中強度，極化和干涉3種不同的信息。

(3)融合3種不同貢獻的分類結果，按照每種貢獻的強度均分為3類，融合后圖像被分割成了27類。將此結果作為初始分類結果啟動算法中的外層迭代。只要類別數不是最佳類別數，每次外層迭代通過類類的聚合將類別數減少1類。

(4)在某一特定類別數情況下，在內層循環中，利用EM迭代和LabelCost能量優化算法來改善分類結果，以獲得穩定的分類結果。

(5)在獲得穩定的分類結果后，利用BIC準則判斷是否為最佳類別數。如果不是最佳類別數，進行類的合并，重新開始進行內層循環。如果為最佳類別數，則跳出循環，并輸出最佳類別數下的分類結果。

6 實驗結果與分析

為了驗證算法的有效性，本文利用E-SAR德國Oberpfaffenhofen 地區的極化干涉 SAR數據和CETC38的機載SAR海南陵水地區極化干涉SAR數據進行實驗。Oberpfaffenhofen 地區的數據，其波段為L波段，分辨率為3.0 m×2.2 m，圖像大小為1300像素×1200像素，平臺高度為3 km，視角從25°變化到 60°。通過分析該地區的光學遙感圖像，并結合地理坐標信息，標記對應的地面實況(ground truth)。海南陵水地區數據，其波段為X波段，分辨率為0.5 m×0.5 m，圖像大小為1200像素×400像素，平臺高度大約是7 km，視角為45°。通過實地考察標記了對應的地面真實圖。

圖2為Oberpfaffenhofen 地區數據分類結果，圖2(b)-圖2(i)分別為4-11類別數下的分類結果。從結果對比中可以看出，類別數在7類左右時，分類結果會比較好。圖2(j)為不同類別下BIC準則函數的曲線圖，曲線在8類時達到最小值，說明通過BIC準則判定最佳類別數為8類，這符合前面對類別數目的分析，在8類的情況下也獲得了好的分類結果，說明了BIC準則判定的有效性。

如圖3所示，圖3(b)-圖3(h)分別為海南陵水地區數據5-11類別數下的分類結果。從圖3(i)中可以看到，BIC準則函數與類別數的變化曲線在第6類時取得最小值。因此確定最佳類別數為6類，對應的分類結果也好于其他類別數下的分類結果。同時，從分類結果圖中也可以看到，在加入了標號代價項后，分類結果的噪聲干擾現象得到了很好的抑制，分類目標區域也保持了很好的完整性。

圖2 Oberpfaffenhofen 地區數據不同類別數下的分類結果

圖3 海南陵水地區數據不同類別數下的分類結果

為了定量分析分類結果的好壞，引入純度(Purity)和條件熵(Conditional Entropy, CE)參量來對分類結果進行評估。純度和條件熵的定義如下：

其中q為真實的類別(class)數目(人為設定)，k為實際分類所得類別(cluster)數目。表示原本屬于第i種類別而最后被分為第r種類別的數據量大小。純凈度越高，熵就越低，說明非監督分類結果越好。表1和表2分別為Oberpfaffenhofen地區和海南陵水地區數據分類純度和條件熵比較結果。方法1和方法2分別是用FastPD能量優化(沒有考慮標號代價項)和LabelCost能量優化的非監督分類算法。

從表中可以看出，隨著類別數的增加純度會增大，然后趨于穩定。Oberpfaffenhofen地區數據的純度在7類附近開始趨于穩定，說明最佳類別數為7類左右。海南陵水地區數據的純度在 6類附近開始趨于穩定，說明最佳類別數為 6類左右。方法2使用了LabelCost能量優化算法，該優化算法不僅考慮了數據代價項和平滑代價項的影響，還考慮了標號代價項的影響，其分類結果更好，表現為純度更高，條件熵更低。在海南陵水地區的數據實驗結果中，其效果更好。

表1 Oberpfaffenhofen地區數據純度和條件熵比較結果

表2 海南陵水地區地區數據純度和條件熵比較結果

7 結論

本文提出了一種改進的極化干涉 SAR非監督分類算法，通過利用LabelCost能量優化，有效地抑制了噪聲對分類結果的影響，目標區域完整性也得到了很好的保持。同時，利用BIC準則確定了非監督分類的最佳類別數，并在最佳類別數下獲得了良好的分類結果。

[1]Cloude S R and Papathanassiou K P. Polarimetric SAR interferometry[J].IEEE Transactions on Geoscience and Remote Sensing, 1998, 35(5): 1551-1565.

[2]Ferro-Famil L, Pottier E, and Lee J S. Unsupervised classification and analysis of natural scenes from polarimetric interferometric SAR data [C]. Proceedings of International Geoscience and Remote Sensing Symposium(IGARSS),Sydney Australia, July 7-13, 2001: 2715-2717.

[3]楊震, 楊汝良, 劉秀清, 等. SAR 圖像的極化干涉非監督Wishart分類方法和實驗研究[J]. 電子與信息學報, 2004,26(5): 752-759.

Yang Zhen, Yang Ru-liang, Liu Xiu-qing,et al.. Study of polarimetric interferometric Wishart classification of SAR images[J].Journal of Electronics&Information Technology,2004, 26(5): 752-759.

[4]Neumann M, Reigber A, and Ferro-Famil L. Data classification based on PolInSAR coherence shapes[C].Proceedings of International Geoscience and Remote Sensing Symposium(IGARSS), Seoul, Korea, July 25-29, 2005:517-519.

[5]談璐璐, 楊汝良, 商建, 等. 利用Shannon熵參數的極化干涉SAR圖像非監督分類[J]. 電子學報, 2010, 38(10): 2264-2267.

Tan Lu-lu, Yang Ru-liang, Shang Jian,et al.. Unsupervised PolInSAR image classification with shannon entropy parameters[J].Acta Electronica Sinica, 2010, 38(10):2264-2267.

[6]Yan W, Yang W, Liu Y,et al.. Unsupervised classification of PolInSAR image based on shannon entropy characterization[C]. Proceedings of International Conference on Signal Processing Proceedings(ICSP), Oct. 24-28, 2010: 2192-2195.

[7]Yan W, Yang W, Sun H,et al.. Unsupervised Classification of PolInSAR data Based on shannon entropy characterization using iterative optimization[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing(JSTARS), 2011, 4(4): 949-959.

[8]代登信. 高分辨率SAR圖像分類研究[D]. [碩士論文], 武漢大學, 2010.

Dai Deng-xin. Study on high-resolution SAR image classification[D]. [Master dissertation], Wuhan University,2010.

[9]J?ger M, Neumann M,et al.. A self initializing PolInSAR classifier using interferometric phase differences[J].IEEE Transactions on Geoscience and Remote Sensing, 2007,45(11): 3503-3518.

[10]Cao F, Hong W, Wu Y R,et al.. An unsupervised segmentation with an adaptive number of clusters using the SPAN H-α-A space and the complex Wishart clustering for fully polarimetric SAR data analysis[J].IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3454-3467.

[11]Delong A, Osokin A, Isack H.N,et al.. Fast approximate energy minimization with label costs [C]. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco USA, Jan. 13-18, 2010:2173-2180.

[12]Morio J, Réfrégier P,et al.. A characterization of shannon entropy and bhattacharyya measure of contrast in polarimetric and interferometric SAR image[J].Proceedings of IEEE, 2009, 97(6): 1097-1108.

[13]Delong A, Osokin A, Isack H N,et al.. Fast approximate energy minimization with label costs[J].InternationalJournal of Computer Vision, 2012, 96(1): 1-27.