銳邊突風對大展弦比機翼的氣動彈性響應影響
劉伏虎,馬曉平
(西北工業大學無人機特種技術國家重點實驗室,陜西西安 710065)
引言
現代飛行器設計日益要求高速度和高機動性,使得飛行器日益呈現出輕結構和大柔性的特點,因此氣動彈性的動穩定性和動力響應問題變得日益突出[1]。氣動彈性動穩定性主要研究顫振問題,動力響應主要討論氣動彈性系統在突風作用下引起的氣動彈性響應問題。文獻[2]以二元機翼為對象,利用Jones氣動力近似方法建立了氣動彈性響應模型,研究了銳邊突風對系統氣動彈性響應的影響。文獻[3]以大展弦比均勻直機翼為對象,求解一階扭轉和一階彎曲情況下系統的顫振速度,利用準定常氣動力模型研究了銳邊突風二元機翼以及直機翼的氣動彈性響應影響。
本文將以大展弦比均勻直機翼為對象,以非定常氣動力為基礎,建立系統響應模型,采用V-g法在二階扭轉和二階彎曲模態下求解系統的顫振速度。以Kussner函數為基礎,建立銳邊突風模型,研究銳邊突風對系統氣動彈性響應的影響。
1 建立模型
設大展弦比均勻直機翼的半展長為l,單位展長質量為m。圖1為其剖面示意圖。圖中,b為翼型的半弦長;a為翼弦中點到彈性軸的距離占半弦長的百分比,彈性軸在半弦線之后a>0,彈性軸位于距離機翼弦線中點ab處;xα為重心與彈性軸的距離占半弦長的百分比,重心在彈性軸之后xα>0,重心與彈性軸的距離為xαb。

圖1 剖面示意圖
設彈性軸彎曲變形為w(y),向上為正,扭轉變形為α(y),迎風抬頭為正;機翼為等截面,其彎曲剛度和扭轉剛度分別為EI和GJ,均為常數;機翼的彎曲和扭轉模態階數分別為Nw和Nα,機翼彎曲振型和扭轉振型函數分別為ψi(y)和φi(y);Sα=mxαb為單位展長機翼對彈性軸的質量靜矩,Iα=mr2αb2為單位展長機翼對彈性軸的質量慣性矩。
通過推導得到系統勢能和動能的表達式,以及系統做的虛功,利用拉格朗日方程得到模態坐標下機翼的運動方程為:
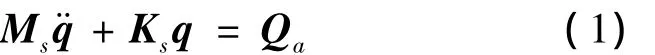
其中:
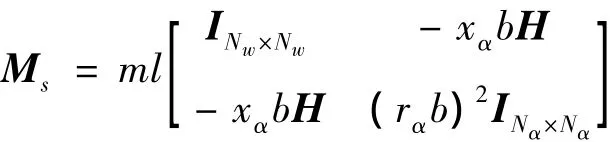
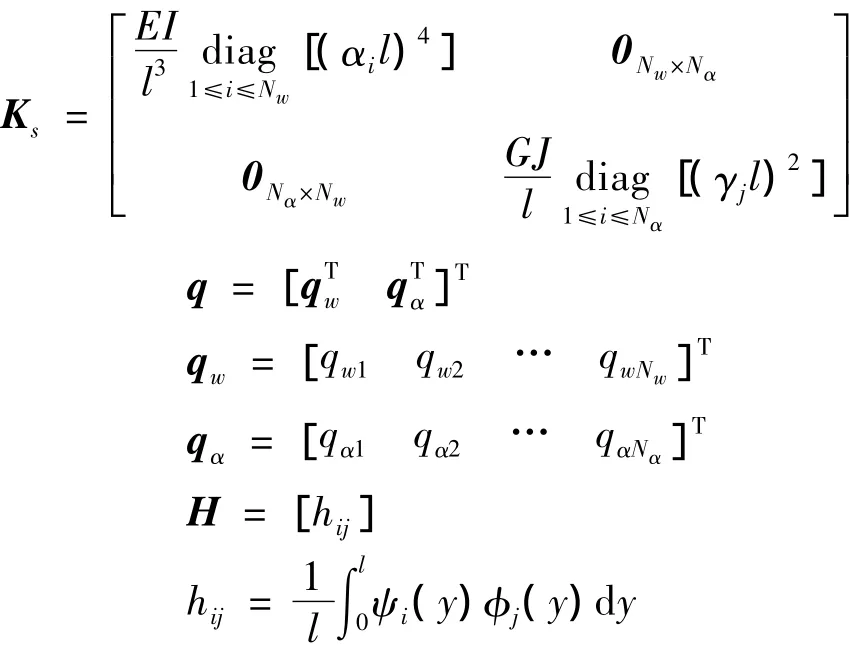
式中,i=1,2,…,Nw;j=1,2,…,Nα。
大展弦比均勻直機翼彎曲振型和扭轉振型的函數表達式為[1]:
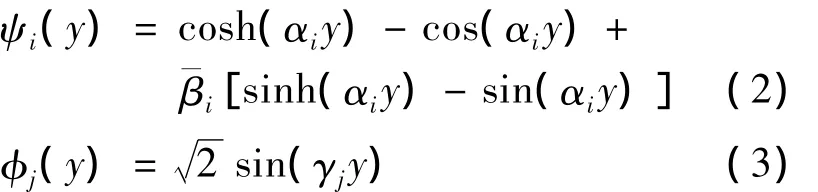
其中:
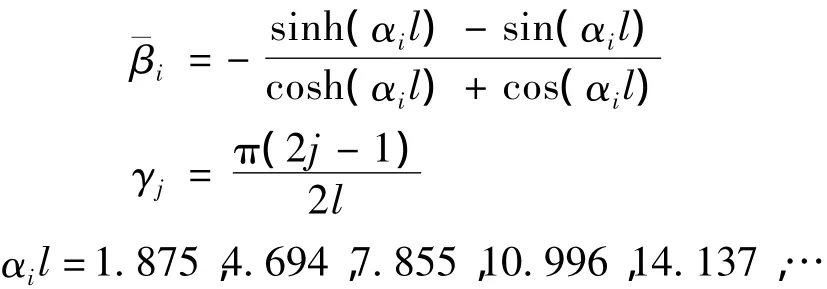
單位展長二元機翼所受氣動力為[4]:
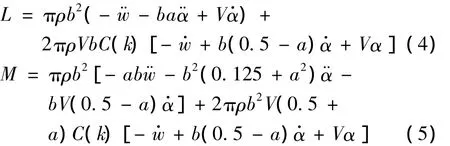
由模態轉換和模態振型函數之間的正交性,可得系統氣動力表達式為:
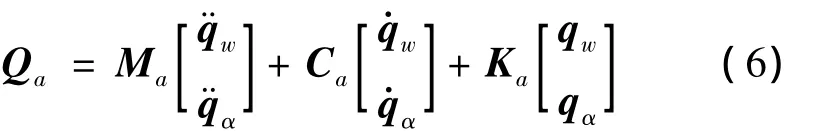
其中:
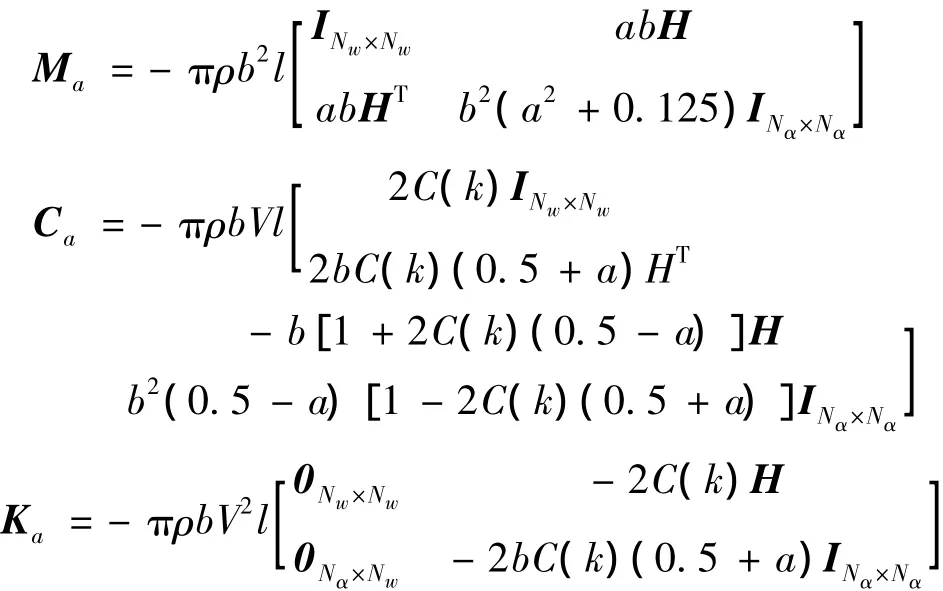
2 銳邊突風的影響
模態坐標下銳邊突風氣動力和力矩表達式可以
寫為如下形式[5]:
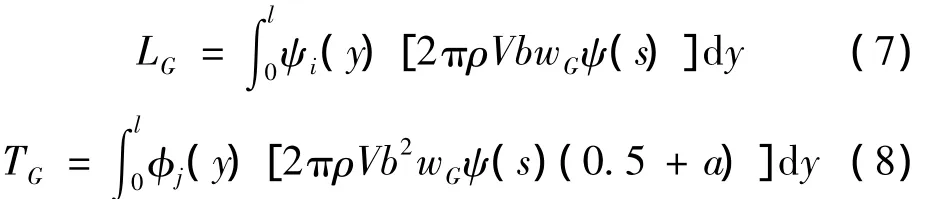
式中,ψ(s)=1-e-0.13s/2-e-s/2為 Kussner函數。將式(2)和式(3)代入式(7)和式(8)得到:
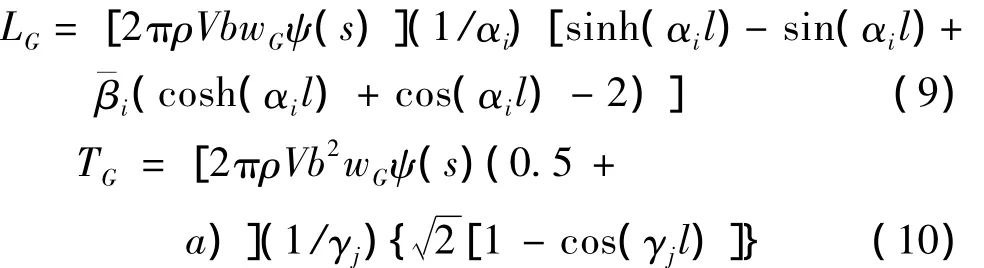
上式即為銳邊突風QG=[LGTG]T的表達式。在研究系統響應時,需要將系統表達在時域空間中,系統中Theodorsen函數C(k)的Wagner近似形式見文獻[6]。
引入空氣動力狀態變量后單位展長機翼非定常氣動力可重新表達為:
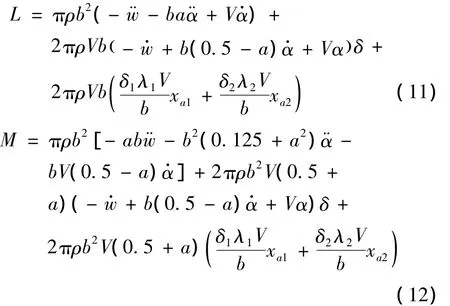
式中,δ=1 -δ1-δ2。
在模態坐標下xa滿足自身運動的狀態空間表達式為:
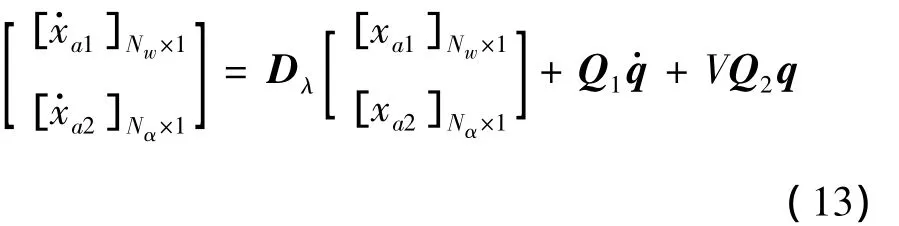
其中:
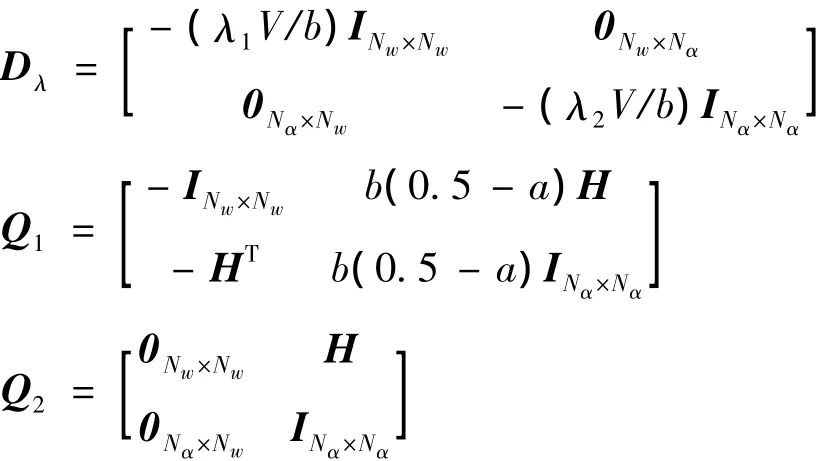
這樣,系統運動方程可重新表達為:
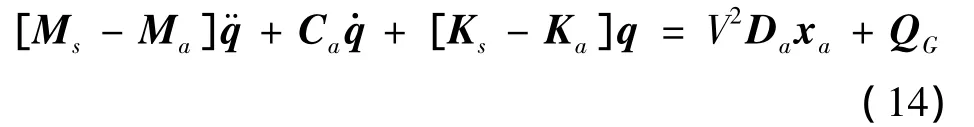
式中的空氣動力相關矩陣重新寫為:
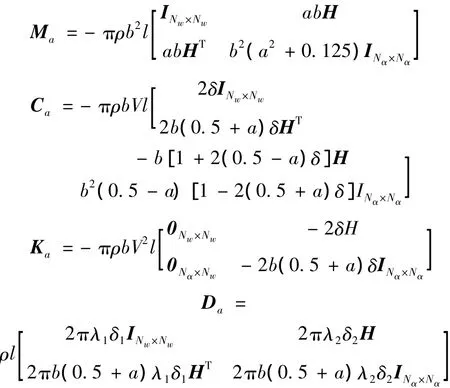
建立系統狀態空間方程如下:

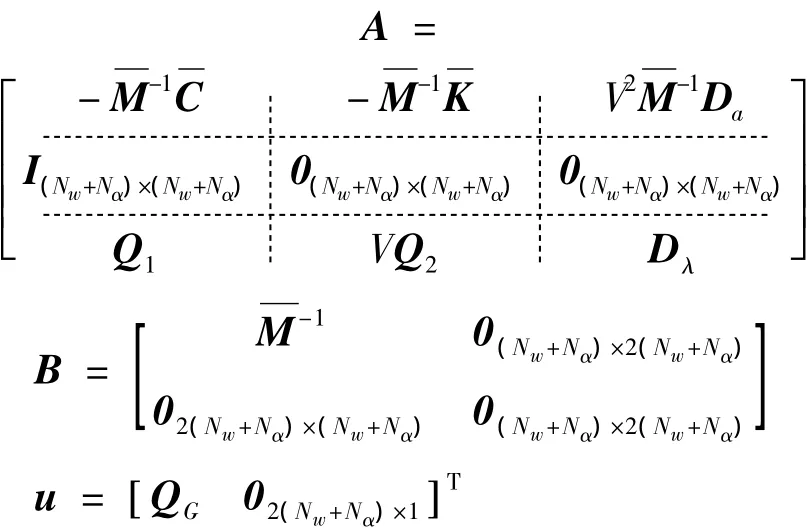
3 仿真分析
本文采用的機翼參數為:xα=0.4,a=-0.2,m=(19.6/l)kg/m,l=1 m,b=0.0915 m,Iα=0.1236 kg·m2,EI=35.96 N·m2,GJ=25.94 N·m2,引入人工結構阻尼g,令q=eiωt,通過V-g法求解系統的顫振速度,取系統二階彎曲和二階扭轉模態,仿真結果如圖2所示。由圖2可以看出,一階扭轉先出現發散,計算得到系統的顫振速度VF=33.2 m/s,顫振頻率為fF=3.15 Hz。
由于系統一階扭轉先出現發散,因此取一階彎曲和一階扭轉模態研究銳邊突風對系統氣動彈性響應的影響,突風速度wG=2 m/s,仿真初始條件為x0= [0 0 0.01 0.2 0 0]T,響應結果如圖3~圖5所示。從圖中可以看出,加入銳邊突風后,V<VF時系統為收斂振蕩,V=VF時系統為等幅振蕩,V>VF時系統為發散振蕩。可以得出VF并未改變,而系統的響應振幅變大。從系統的狀態空間方程出發,影響系統VF的因素主要由A的特征值決定。當加入突風后,其特征值并未改變;從系統結構出發,突風并未改變系統本身的機構參數,加入突風相當于給了系統一個外加的擾動力,因此系統響應只是振幅改變。
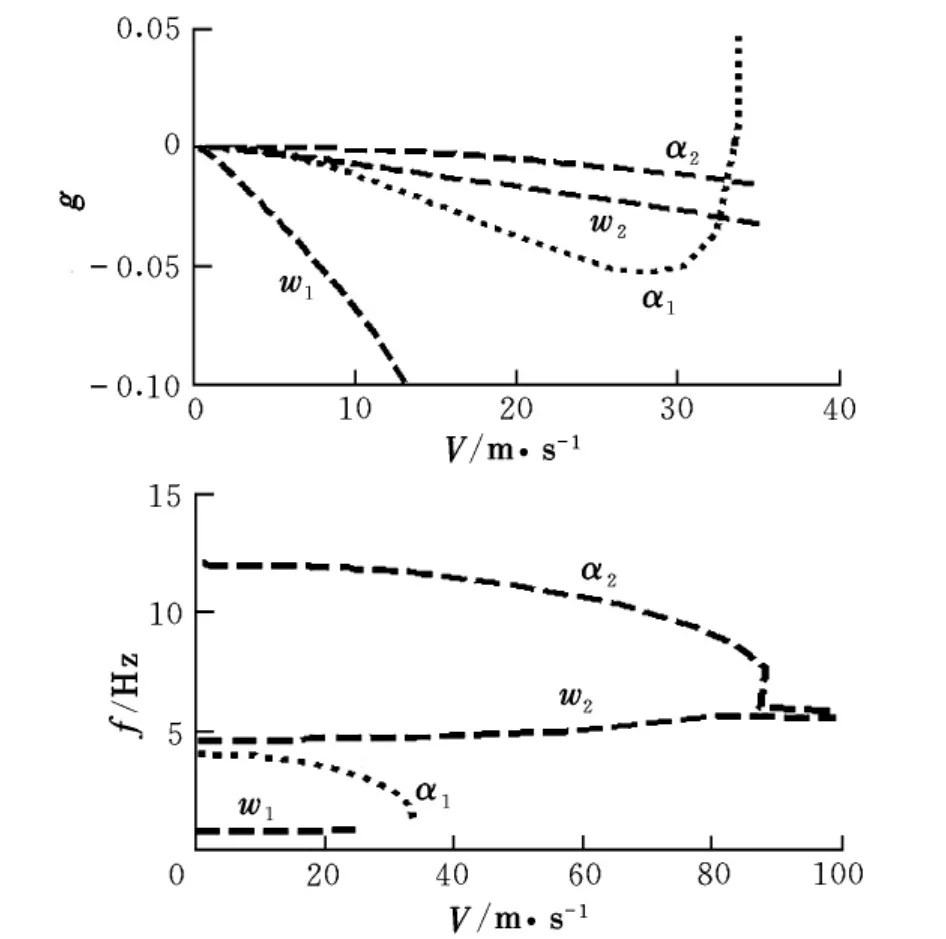
圖2 系統顫振示意圖(Nw=2,Nα=2)
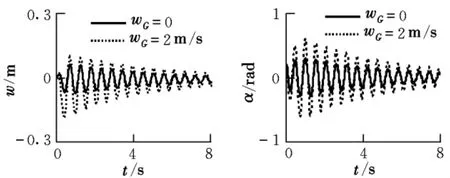
圖3 V=0.99VF時加入突風后的翼尖響應
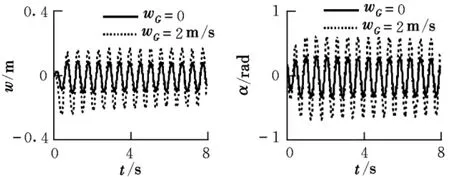
圖4 V=VF時加入突風后的翼尖響應
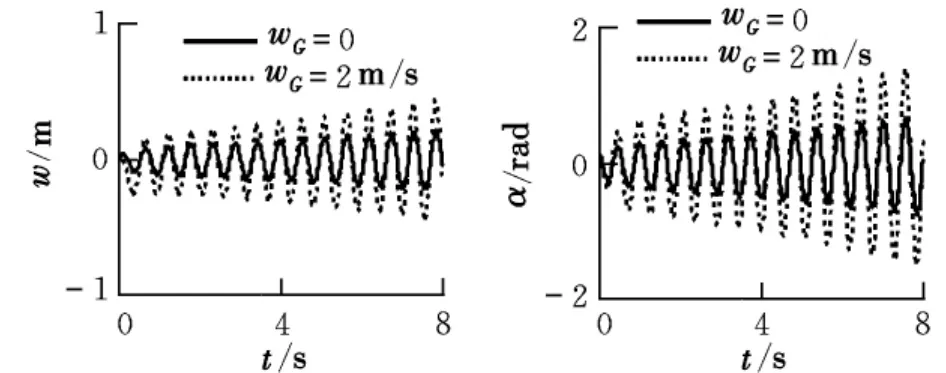
圖5 V=1.01VF時加入突風后的翼尖響應
4 結束語
本文以大展弦比直機翼為對象,基于非定常氣動力理論建立了系統的氣動彈性運動方程,并取二階彎曲和二階扭轉模態求得系統的顫振速度。建立了彎曲和扭轉模態階數為Nw和Nα下的系統狀態方程,研究了銳邊突風分別在小于、等于和大于顫振速度下對系統的氣動彈性響應的影響。結果表明,銳邊突風增大了系統響應的振幅。整個系統的建模過程對下一步研究飛行器突風響應有一定的參考意義。
[1]趙永輝.氣動彈性力學與控制[M].北京:科學出版社,2007.
[2]Kargarnovin M H,Mamandi A.Aeroelastic response for pure plunging motion of a typical section due to sharp edged gust using jones approximation aerodynamics[J].World Academy of Science,Engineering and Technology,2007,36(1):154-161.
[3]Haddadpour H,Shams S,Kheiri M.Sharp edge gust effects on aeroelastic behavior of a flexible wing with high aspect ratio[R].AIAA-2005-838,2005.
[4]Theodorsen T.General theory of aerodynamic instability and the mechanism of flutter[R].National Advisory Commission for Aeronautics,NACA-TR-496,1949.
[5]Earl H D.A modern course in aeroelasticity[M].Kluwer Academic Publishers,1995.
[6]Sutherland A N.A demonstration of pitch—plunge flutter suppression using LQG control[R].ICAS2010,2010.

