一種虛擬目標點的彈道迭代確定方法
王繼平,肖龍旭,王安民,林紅斌,杜林峰
(1.第二炮兵裝備研究院,北京 100085;2.中國人民解放軍96271部隊,河南 洛陽 471000)
引言
為了提高彈道導彈的精度,一方面要提高導航設備的精度,另一方面要采用先進的制導方法,減小制導方法誤差。基于虛擬目標點的閉路制導方法是一種高精度的顯示制導方法,它首先要確定虛擬目標點。傳統虛擬目標點的確定是基于標準彈道,對地球扁率和再入阻力影響進行修正,但存在百米左右的修正誤差[1]。當實際彈道偏離標準彈道,虛擬目標點變化較大時,采用標準彈道確定的虛擬目標點進行閉路制導會產生較大的方法誤差。若是處于彈道設計階段,在標準彈道閉路制導段還沒有確定的情況下,傳統方法失去了標準彈道關機點基準,確定不了虛擬目標點。
本文的彈道迭代確定方法卻能適應這一情況,精確確定虛擬目標點。在飛行過程中,可采用自由飛行彈道的快速計算方法,實時迭代計算虛擬目標點,保證了虛擬目標點相對實際彈道的精度。
1 虛擬目標點的彈道迭代計算思想
虛擬目標點彈道迭代計算分為射前標準彈道迭代和彈上實時迭代計算。射前標準彈道迭代計算量大,計算時間相對較長。文獻[2-3]分別對標準彈道迭代作了相關研究,雖然文獻[3]的彈道迭代效率較高,但是目前的彈載計算機仍無法實現彈上實時計算,況且對于虛擬目標點的迭代計算,文獻[3]的方法不再適用。本文采用類似文獻[2]的彈道迭代方法進行虛擬目標的確定,其精度相對標準彈道高得多。彈上實時迭代計算要求計算量小,因而采用自由段飛行彈道的快速計算方法,且彈上采用高性能計算機,才能保證實時性要求。虛擬目標點確定精度由自由段飛行彈道計算精度和再入阻力實時修正精度決定。
射前標準彈道迭代計算思想為:虛擬目標點一般離真實目標點不遠,首次彈道計算時可以假設虛擬目標點位于目標點,之后按修正的虛擬目標點進行計算。在閉路制導段進行需要速度增量計算,并進行導引和關機控制,再經過被動段彈道解算落點,通過大地貝賽爾反解[2]求取落點偏差。然后根據落點偏差信息反復修正虛擬目標點,直到落點偏差為零,此時對應的虛擬目標點就是要求的虛擬目標點,同時也確定了閉路制導段。
彈上實時迭代計算思想為:在飛行過程中,當導彈離關機點不遠時,對虛擬目標點進行實時迭代修正。以當前需要速度、位置、導彈飛行時間作為關機狀態,利用自由飛行彈道的快速計算方法,計算地球扁率對落點的影響;采用擬合方法計算再入阻力對落點的影響;對兩者進行修正確定新的虛擬目標點,再以新的虛擬目標點迭代計算需要速度;依此法再次確定虛擬目標點,比較相鄰兩次虛擬目標點的經緯差,當小于要求值時,迭代結束,即得到當前狀態對應的虛擬目標點。
下面首先給出閉路制導的需要速度計算方法和導引關機控制策略,在此基礎上探討虛擬目標點的彈道迭代確定方法。
2 閉路制導導引與關機控制
2.1 閉路制導需要速度計算
閉路制導需要速度是根據導彈當前狀態和虛擬目標點,通過橢圓彈道迭代求取的。需要速度可以固定關機點傾角、被動段飛行時間、再入傾角等為條件進行迭代,本文擬采用固定關機點傾角為條件,具體迭代計算公式見文獻[1]。
2.2 閉路制導導引
閉路制導方法常在大氣層外使用,僅由推力提供視加速度。為了使導彈耗能最少,按“方向與速度增量Δva一致”的原則進行導引控制。設導彈制導控制周期為T,推力沿彈體軸向,則推力控制方向為:

式中,φa,ψa,γa為彈體系相對發射慣性坐標系的絕對俯仰角、絕對偏航角和絕對滾動角;vgxa,vgya,vgza為需要速度增量在發射慣性坐標系下的分量。
2.3 閉路制導關機控制
關機控制采用如下關機條件:
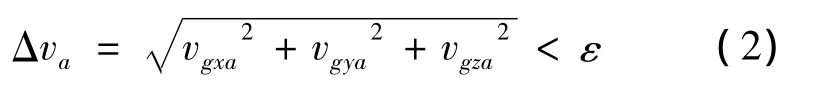
式中,ε為一實際要求的小量。
3 虛擬目標點的標準彈道迭代計算
導彈虛擬目標點的標準彈道迭代計算在射前完成,彈道解算采用龍格-庫塔轉阿達姆茨數值積分法,在閉路制導段按式(1)和式(2)進行導引和關機控制,彈道迭代參數為虛擬目標點經緯度(LM,BM)。其迭代方法與步驟如下:
(1)令當前虛擬目標點經緯度等于目標點經緯度(LT,BT):
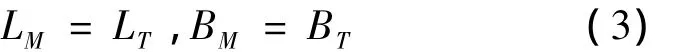
(2)計算以當前虛擬目標閉路制導產生的落點偏差(ΔL,ΔH)對(LM,BM)的偏導數矩陣。
分別給(LM,BM)一個小擾動(δLM,δBM),得:
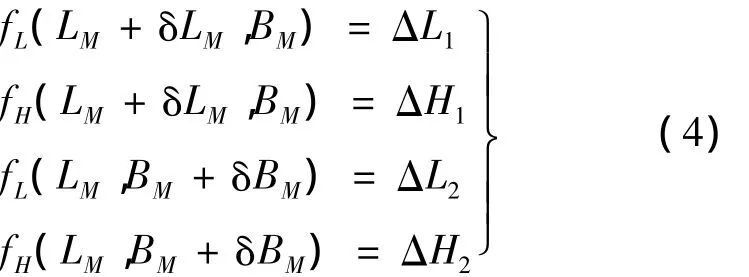
根據上式,落點偏差(ΔL,ΔH)對(LM,BM)的偏導數矩陣為:
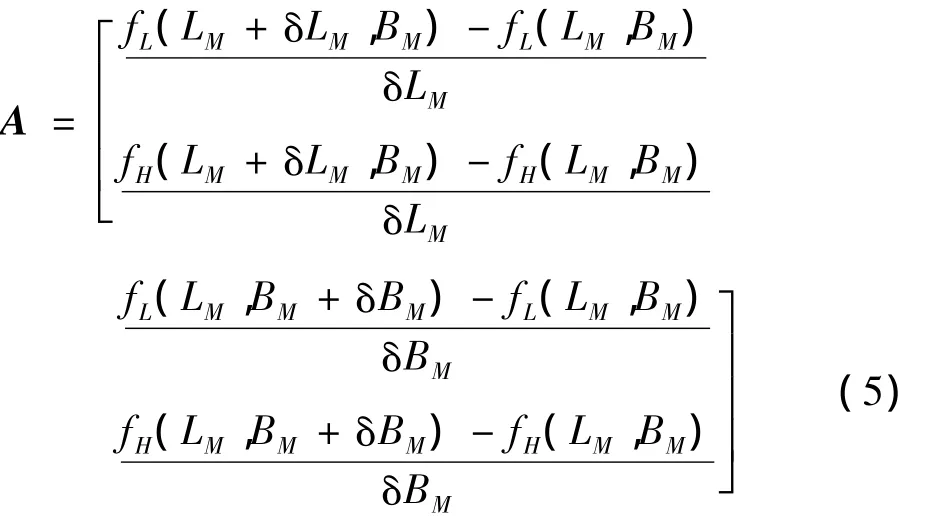
(3)計算當前虛擬目標改變量(ΔLM,ΔBM)
設虛擬目標變化了(ΔLM,ΔBM)后,落點偏差為零,則:
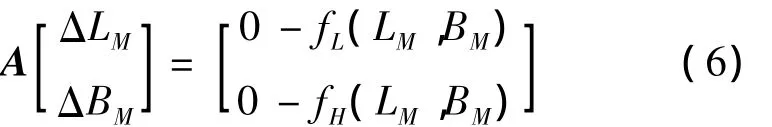
根據式(6),得:
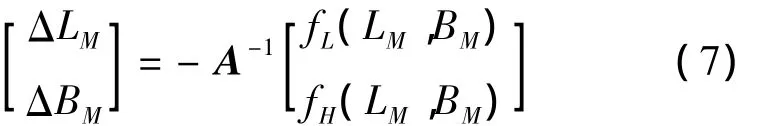
(4)計算以虛擬目標(LM+ΔLM,BM+ΔBM)進行閉路制導產生的落點偏差;
(5)以LM=LM+ΔLM,BM=BM+ΔBM為當前虛擬目標,重復步驟(2)~(4),直至落點偏差ΔL<ε1,ΔH<ε2(ε1,ε2為要求小量),此時對應的(LM,BM)即為迭代確定的虛擬目標點。
4 虛擬目標點的彈上迭代實時計算
導彈虛擬目標點的彈上實時迭代計算,采用自由飛行彈道的快速計算方法確定地球扁率影響,采用擬合計算方法確定再入阻力影響,在閉路制導段按式(1)和式(2)進行導引和關機控制,彈道迭代參數為虛擬目標點經緯度(LM,BM)。首先給出自由飛行彈道的快速計算方法和再入阻力影響的實時修正方法。
4.1 自由飛行彈道的快速計算方法
常用的自由飛行彈道的快速計算方法有:自由段彈道解析解的非正交分解法[4-6]、中間軌道法[7]和基于狀態空間攝動的自由段彈道解析法[5-6]等。其中非正交分解法的落點偏差精度在百米左右;中間軌道法、基于狀態空間攝動的自由段彈道解析法落點偏差計算精度都在40 m以內[5]。可根據需要選擇相應的自由段彈道快速計算方法,分別令地球扁率系數J為常值和J=0,計算落點偏差,即為地球扁率對落點的影響。
4.2 再入阻力影響的實時修正方法
當導彈再入大氣層后,要受到空氣動力的作用。假定彈頭是靜穩定的,彈頭燒蝕是均勻的,即是軸對稱的,則可認為再入段導彈的攻角為零。再入段氣動阻力的影響是再入點高度、再入點速度、彈道傾角及彈頭的阻重比的函數。若導彈型號已定,彈道傾角固定,則再入阻力影響只是落速和再入點高度的函數,可將射程角偏差(Δβx)擬合成再入點速度Vc、再入點高度hc的函數[8]。
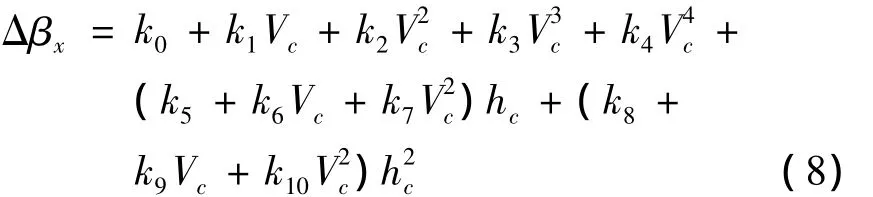
式中,ki(i=0,…,13)為擬合系數。從而可根據射程角偏差確定落點經緯度偏差:
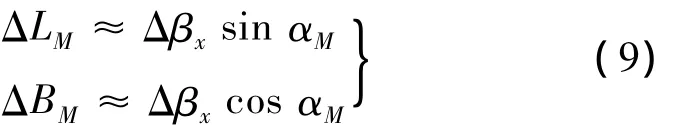
式中,αM為落點射向方位角。
4.3 彈上迭代實時計算方法與步驟
虛擬目標點的彈上迭代實時計算方法與步驟如下:
(1)以真實目標點為虛擬目標點(LM1,BM1),計算需要速度vRxa,i,vRya,i,vRza,i,其中,vRxa,i,vRya,i,vRza,i為需要速度在發射慣性坐標系下的分量,下標i代表彈上制導周期數;
(2)以需要速度和當前位置、時間為當前狀態,采用自由飛行彈道的快速計算方法計算再入速度和地球扁率引起的落點偏差(ΔLM1,ΔBM1);
(3)將再入速度和再入高度代入擬合公式(8),計算再入阻力引起的落點偏差(ΔLM2,ΔBM2);
(4)對地球扁率和再入阻力引起的落點偏差進行修正,獲得虛擬目標點:
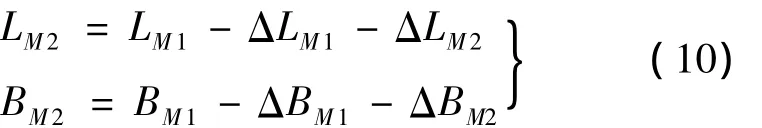
(5)當|LM,j+1-LM,j|<ε1,|BM,j+1-BM,j|<ε2(j=1,2,…,n)時,停止迭代;否則以虛擬目標點(LM2,BM2)計算需要速度vRxa,i,vRya,i,vRza,i,轉入(2)。
5 仿真算例及結果分析
5.1 算例條件

5.2 算例結果
經仿真計算,標準彈道迭代經兩次迭代修正后達到迭代要求。虛擬目標彈上迭代計算的每個制導周期經過兩次迭代達到迭代要求。仿真計算機平臺為CPU主頻2.83 GHz,四核處理器;內存3.37 G;操作系統Windows xp2,采用C語言在VC++6.0編程環境下運行迭代代碼耗時0.141 ms,可見在高性能計算機上實現實時計算是可能的。
虛擬目標點迭代結果見表1。

表1 虛擬目標點迭代結果
由表1可知,按迭代后的虛擬目標點進行閉路制導,落點偏差在1 m內。
按最終的虛擬目標進行閉路制導,其導彈速度(Vx,Vy,Vz)和需要速度(Vrx,Vry,Vrz)隨時間的變化曲線見圖1,俯仰角、偏航角隨時間的變化曲線見圖2,俯仰角、偏航角迭代終值與初值之差(Δφa,Δψa)隨時間的變化曲線見圖3。
由圖3可知,隨虛擬目標點變化,閉路制導的俯仰角、偏航角也隨之變化。虛擬目標點迭代確定后,閉路制導段也同時確定。
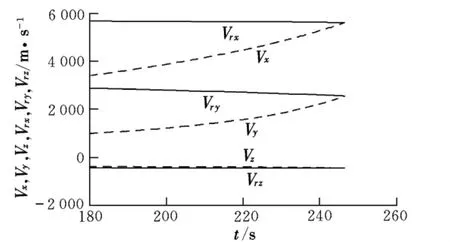
圖1 導彈速度和需要速度隨時間的變化曲線

圖2 φa和ψa隨時間的變化曲線
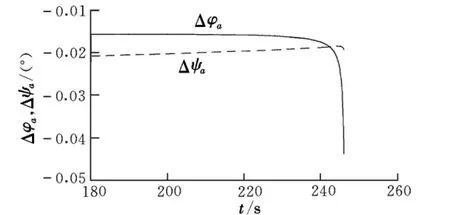
圖3 Δφa和Δψa隨時間的變化曲線
當實際彈道與標準彈道偏離不大時,射前標準彈道迭代確定的虛擬目標點精度高,按其進行閉路制導,方法誤差在80 m內;當導彈推力產生大偏差時,實際彈道偏離標準彈道很大,按射前裝訂的虛擬目標點進行閉路制導誤差達300 m以上,在飛行過程中采用實時迭代計算的虛擬目標點進行閉路制導,落點誤差可精確到100 m左右。虛擬目標點實時迭代計算隨時間的變化曲線如圖4所示。
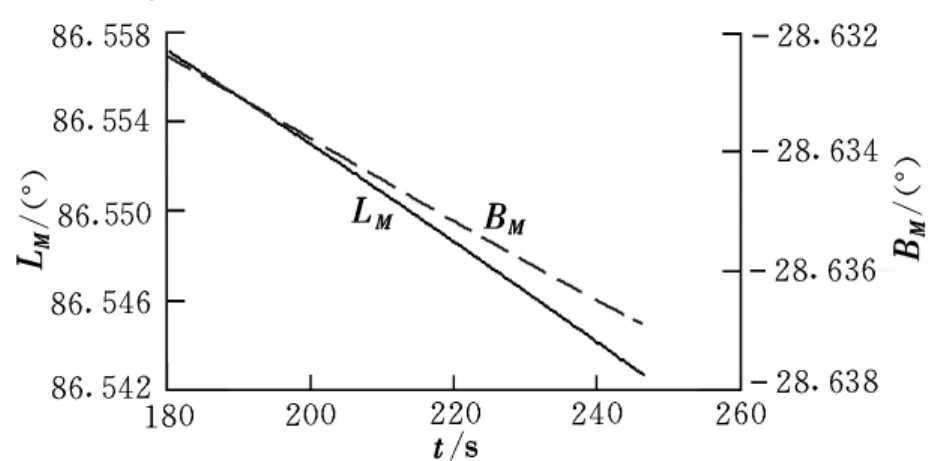
圖4 虛擬目標隨時間的變化曲線
可見,在閉路制導段開始與結束虛擬目標點變化較大,而起關鍵作用的是最終的虛擬目標點,因而整個閉路制導段實時迭代計算虛擬目標點沒有必要,只需在關機前一小段時間進行迭代計算實時修正即可,之前用地面裝訂虛擬目標諸元制導。
6 結束語
虛擬目標點的射前標準彈道迭代確定方法,在閉路制導段設計時能夠有效發揮其作用,并能根據迭代要求達到所需精度。但由于需要解算彈道,且進行彈道迭代,因而比虛擬目標點的傳統確定方法耗時。虛擬目標點的彈上迭代實時計算方法,由于采用迭代思想同樣能根據迭代要求達到所需精度,但精度限于自由飛行彈道的快速計算精度和再入阻力影響的修正精度。實際使用中,為減小彈上計算負荷,閉路制導段可先按射前裝訂的虛擬目標點進行制導,到關機點前幾秒時,采用虛擬目標點實時迭代計算,根據彈載計算機性能可適當加大迭代計算周期,按實時計算的虛擬目標點進行閉路制導,以提高制導精度。
[1]王繼平,王明海.基于虛擬目標點制導的誤差分析[J].飛行力學,2007,25(4):50-53.
[2]馬丹山,王明海,車明波.彈道導彈的標準彈道迭代方法研究[J].飛行力學,2007,25(4):48-53.
[3]王明海,李邦杰.彈道導彈彈道設計的一種快速迭代方法[J].飛行力學,2007,25(2):76-77.
[4]張毅,肖龍旭,王順宏.彈道導彈彈道學[M].長沙:國防科學技術大學出版社,2005.
[5]李連仲.彈道飛行器自由飛行軌道的解析解法[J].宇航學報,1982,3(1):1-17.
[6]鄭偉.地球物理攝動因素對遠程彈道導彈命中精度的影響分析及補償方法研究[D].長沙:國防科學技術大學,2006.
[7]劉林.人造地球衛星軌道力學[M].北京:高等教育出版社,1992.
[8]肖龍旭,王順宏,魏詩卉.地地彈道導彈制導技術與命中精度[M].北京:國防工業出版社,2009.

