自適應蟻群差分進化算法

拓守恒

（陜西理工學院 計算機系，陜西 漢中723000）

0 引 言

差分進化算法（differential evolution，DE）具有全局探索和局部開發的能力，容易和其他優化搜索混合等特性［1］，在大規模復雜應用研究中取得了較好的效果［2］，但也存在求解精度低等缺點，研究者們為了提高DE算法的性能，做了大量研究和改進。文獻［3］按照個體適應度的差異將個體分成不同的子種群，并針對不同的個體適應度值采用不同的變異算子，以保證在加快算法收斂速度的同時有效地跳出局部極值點。文獻［4］提出一種基于多進化模式協作的差分進化算法，在每次迭代時，總是依次從3種模式中選取一種用于不同個體的進化，從而提高算法的通用性。文獻［5］提出一種帶有隨機變異的動態差分進化算法，在這個算法中，兩種不同的變異策略DE/rand/1和DE/best/1通過線性遞減加權組合策略產生新的變異策略，以便動態利用DE/rand/1和DE/best/1的優點。文獻［6］提出了中心變異差分進化算法，算法在每代變異時，選擇種群的一個中心個體作為基向量，根據參加變異的3個隨機個體向量間的函數適應值的大小關系，確定差向量的方向。上述幾種算法都是針對差分進化算法的某一方面的缺點進行了改進，或者針對某一具體問題的應用性改進，但是往往通用性較差，難以在各種復雜變化的問題中得到好的優化效果。

為了提高DE算法的通用能力，受蟻群算法的啟發，本文提出一種基于蟻群算法的自適應差分進化算法。算法將目前已經取得較好效果的變異算子綜合應用于優化問題中，采用一種改進的多模式并行差分變異策略，不同于文獻［4］，本文采用蟻群算法對差分變異算子的選擇概率進行動態調整，從而提高算法的優化速度、穩定性和通用性。

1 差分進化算法

差分進化（differential evolution，DE）［7］是由Storn和Price于1996年為求解切比雪夫多項式而提出的一種演化算法。DE算法用浮點矢量編碼在連續空間中進行隨機搜索。DE主要采用2種進化算子：差分變異算子和交叉算法進化種群。由于DE算法采用實屬編碼，算法簡單易用，所以在連續域優化問題種得到了廣泛應用［8］。

1.1 差分變異算法性能特征分析

DE算法的關鍵是差分變異算子（differential operator，DO），目前有多種變異進化模式，其一般表示形式為DE/x/u/y/z［4，9］，其中，x表示在差分變異算法中與差異向量進行重組的基準個體，基準個體可以是：當前個體Xi、隨機選取的個體Xrand或者是當前群體的最優個體Xbest；u表示差異向量的生成方式（rand－to－rand，rand－to－best），y表示參與重組的差異向量個數；z表示重組所采用的方式，主要有指數重組方式和二項式重組方式。本文選取下面4個取得較好優化效果的變異進化模式，并對其進行改進：

其中，λ，c1，c2是變異因子，在（0，1）上取值，r是（0，1）上的隨機數。

模式（1）是標準的差分變異進化算法，從種群中隨機選擇個體Xr1、Xr2和Xr3。讓基準個體Xr1和差向量Xr2－Xr3進行重組生成新個體Vi。該算法全局搜索能力強、不容易陷入局部搜索，但收斂速度慢，求解精度低。

模式（3）以當前種群中最優個體Xgbest作為基準個體，從準確中隨機選擇4個個體生成差向量：Xr1－Xr2和Xr3－Xr4，特點是收斂速度快、求解精度高，但對于多模態優化問題，容易陷入局部最優。

模式（2）以隨機個體Xr1作為基準個體，用Xgbest（當前種群中最優個體）和Xpbest（隨機選擇的3個體中最優個體）分別和隨著個體Xr2，Xr3作差，生成差向量：Xgbest－Xr1和Xpbest－Xr2。模式（4）借鑒粒子群優化算法思想，以局部最優個體Xpbest和種群最優個體Xgbest作為基準個體，隨機選擇2個體作差向量。模式（2）、模式（4）結合模式（1）和模式（3）的優缺點，在全局收斂性、局部收斂性和收斂速度等方面做了均衡，增強了算法的通用性，但算法的魯棒性和求解精度任然較低。

上述變異進化模式（2）～模式（4）各自雖然針對差分進化算法的某一方面的缺點進行了改進，但對一些具體問題進行優化時性能表現各異，其一種算法并不能對所有問題通用有效，甚至同一問題在維度不同時（比如100維和200維），同一算法的有效性也有很多差異。為了使差分進化算法具有更強的通用性和魯棒性，文獻［4］隨機從3種變異進化模式中隨機選取一種用于不同個體的進化，雖然使得算法具有更強的通用性，但隨機選取變異模式使得收斂速度明顯降低。文獻［5］中，兩種不同的變異策略DE/rand/1和DE/best/1通過線性遞減加權組合策略產生新的變異策略，算法也僅僅是在全局收斂和局部收斂做了一點平衡。

本文提出一種利用蟻群算法動態選擇差分變異進化模式，算法根據個體進化中各模式對優化問題的有效性對權值進行動態調整，從而提高算法的收斂速度、穩定性和通用性。

2 算法描述

2.1 蟻群算法

蟻群算法（ant colony optimization algorithm，ACO）［10－11］也是新型仿生智能優化算法。ACO算法通過模仿螞蟻尋食過程，利用螞蟻群在尋找食物過程中留下的信息素，探索一條到食物源的最佳路徑［12－13］。

2.2 基于蟻群算法的多模式差分變異

本文提出一種基于蟻群算法的多模式差分變異算法，使群體在進化過程中根據各變異進化算法的有效性動態調整其選擇權值，個體在每代進化中根據變異進化模式（DO1，DO2，DO3，DO4）上的信息素（τ1，τ2，τ3，τ4）的大小采用輪盤賭選擇算法選擇變異算子，如圖1所示。

（1）信息素的更新

設置初始信息素τ1（t0）＝τ2（t0）＝τ3（t0）＝τ4（t0）＝0.25，這樣在進化開始時，各變異算子（DO1，DO2，DO3，DO4）被選中的概率相同。

為了提高進化效率，在個體的進化過程中根據各變異算子對進化所做的貢獻更新信息素。更新規則如下

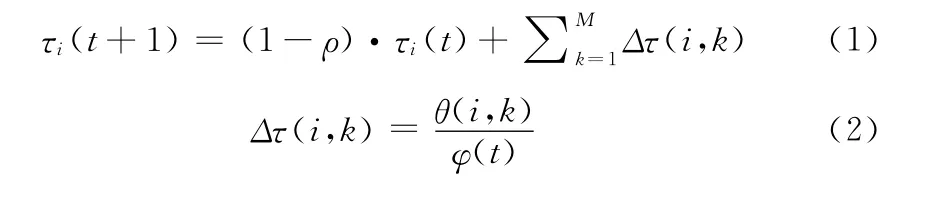
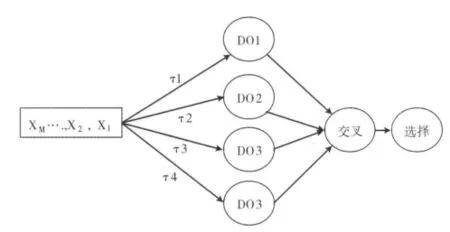
圖1 基于蚊君算法的多模式差分進化過程

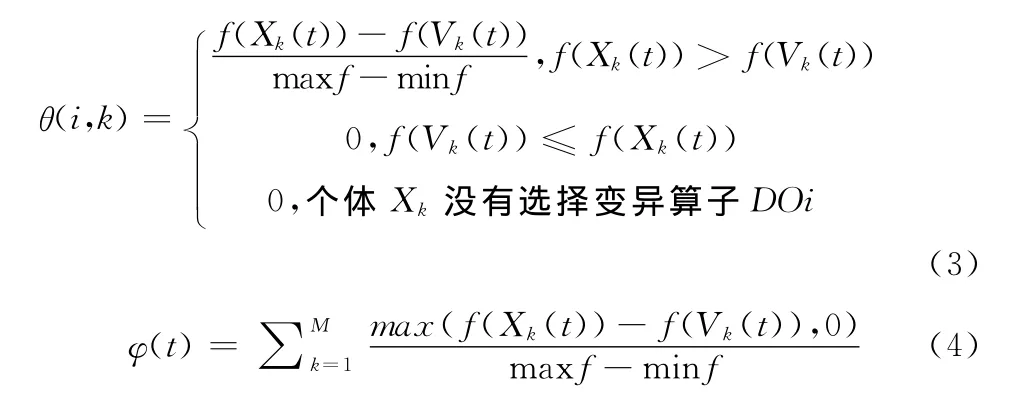
式中：M——種群中個體的數量（螞蟻的數量），i＝1，2，…，M，ρ——信息素的蒸發率。max f、min f——當前種群中個體的最大、最小適應值。

（2）改進的自適應差分變異

本文提出一種自適應的并行變異策略，改進后變異算子可表示為：

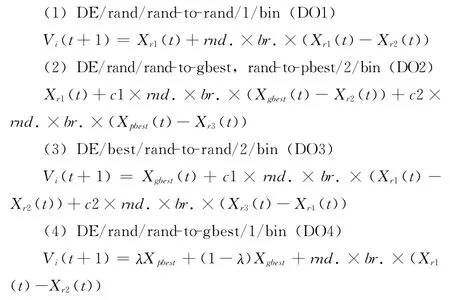
其中，λ＝rand（1，D），rnd＝rand（1，D），rand（1，D）表示在（0，1）上產生一個D維的隨機向量。

br＝｛s1s2，…，sD｝＝round（rand（1，D）＊ex），，（u∈［0.8，1.5］，σ∈［0.7，2］），t是當前進化代數。maxT是最大進化次數。D是維數，round（a）表示對a進行4舍5入取整。“.×”表示向量對應位的乘積，比如：（0.5，0.4，0.7，0.2）.×（1，0，1，0）＝（0.5，0，0.7，0）。

2.3 基于蟻群算法的自適應差分進化算法

算法步驟如下：

（1）參數初始化：設置種群大小 M，交叉概率p，信息素的蒸發率ρ＝0.2，變異參數（u，σ），最大迭代次數maxT，維數D，種群擁擠裁剪最小距離minL，進化終止條件等參數。

（2）在可行解空間內隨機初始化種群。

（3）計算個體的適應度。

（4）利用本文提出的基于蟻群算法的差分變異算法對種群進行一次變異進化。

（5）利用交叉算子和選擇算子對種群進行交叉和選擇。

（6）混沌搜索：選擇種群中最優個體Xgbest進行混沌迭代［14］，最大迭代次數設置為20。

（7）為了避免種群陷入局部搜索，采用種群擁擠距離裁剪策略［15］將種群中擁擠距離＜minL的部分個體剔除。

（8）產生新個體補充到種群，使得種群大小為保持為M。

（9）終止條件判斷。如果迭代次數達到規定最大值或獲得到理想的結果，則結束并輸出結果，否則轉到第（4）步繼續下一代進化。

3 算法仿真分析

為了驗證本文算法的性能，所使用的硬件環境為：方正Pentium 4CPU1.8GHz處理器，512MB內存，算法編碼在MATLAB 2009（a）進行編程實現。測試選取了5個標準benchmark高維多模態測試函數（f1－f5）作為測試用例，將算法測試結果與 MEDE［4］進行比較。在所有測試函數中，設置參數u＝1.0，σ＝1.2。分別測試在維數D＝100和D＝200是的運行結果，讓每個測試各自獨立運行20次，并記錄下平均進化次數（Gens），20次結果的最優值（Best），20次測試的平均值（Mean）及標準方差（Std），見表1。

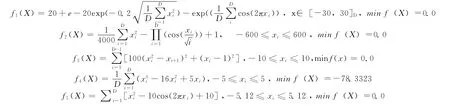
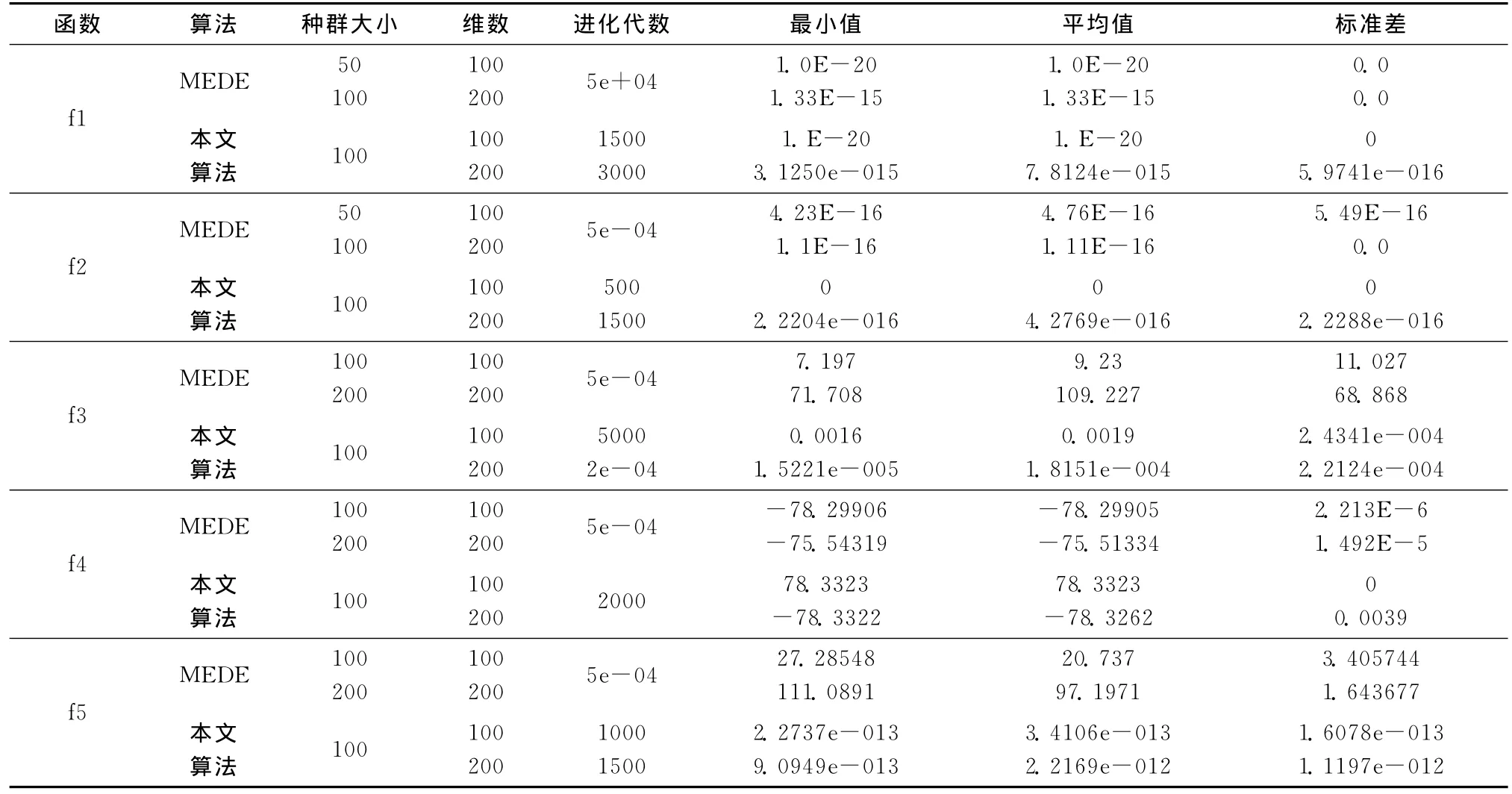
表1 本文算法與MEDE算法在函數f1－f5上的測試結果比較

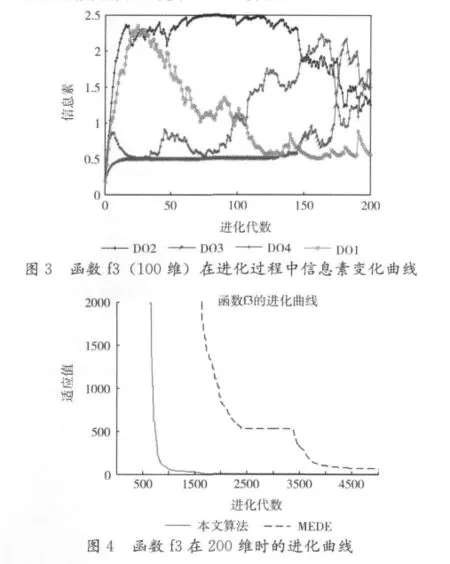
在測試中，實驗同時記錄了不同階段4種變異進化模式上的信息素的變化過程，如圖2、圖3所示。通過圖2和圖3可以看出，對100維的函數f1，進化初期，DO3獲得很高的信息素，DO1一直保持低水平的信息素，DO4在進化后期效果明顯，信息素增加較快。而對函數f3和f1相比，變異進化模式DO1和DO3出現了相反的變化過程。這說明對于不同的問題往往解決方式有差異，本文通過基于蟻群算法的自適應多模式差分變異策略，使得算法面對具體問題時，能夠根據進化的需要自適應的選擇變異模式，從而提高收斂速度和解的精度。

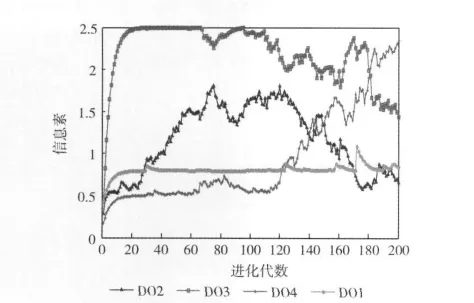
圖2 函數f1（100維）在進化過程中信息素變化曲線

從表1中可以看出，除了測試函數f3之外，其余函數在100和200維都能夠在3000次以內獲得高精度全局近似最優解。觀察20次獨立運行的結果發現，Best、Mean和Std在測試函數f1和f2上與MEDE算法比較接近，而測試函數f3－f5結果具有明顯優勢，并且進化代數和函數的評價次數也遠低于MEDE。圖4是函數f3在200維時的進化收斂曲線，由圖可以明顯看出，本文算法不論是收斂速度還是解的精度都明顯優于MEDE算法。

4 結束語

傳統差分進化算法存在收斂速度慢、魯棒性低和通用性差等特點，并且同一變異算子對不同問題時，性能存在較大差異，甚至對同一函數在維度不同時也存在差異。為了提高算法的通用性，本文在傳統的差分進化算法基礎上提出了一種基于蟻群算法的自適應多模式差分進化算法，算法根據各變異算子對當前種群的進化效果進行動態調整各變異模式上的信息素，使得各變異算子發揮其最大性能。

［1］CHI Yuan－cheng，FANG Jie，CAI Guo－biao.Hybrid optimization algorithm based on differential evolution and particle swarm optimization［J］.Computer Engineering and Design，2009，30（12）：2963－2965（in Chinese）.［池元成，方杰，蔡國飆.基于差分進化和粒子群優化算法的混合優化算法［J］.計算機工程與設計，2009，30（12）：2963－2965.］

［2］TUO Shou－heng，WANG Wen－yong.Self－adaptive differential evolution algorithm based on orthogonal and niche elite for highdimensional multi－modal optimization［J］，Journal of Computer Applications，2011，31（4）：1094－1098（in Chinese）.［拓守恒，汪文勇.求解高維多模優化問題的正交小生境自適應差分演化算法［J］.計算機應用，2011，31（4）：1094－1098.］

［3］LU Feng，GAO Li－qun.Adaptive differential evolution algorithm based on multiple subpopulation with parallel policy［J］.Journal of Northeastern University（Natural Science），2010，31（11）：1538－1541（in Chinese）.［盧峰，高立群.基于多種群的自適應差分進化算法［J］.東北大學學報（自然科學版），2010，31（11）：1538－1541.］

［4］HE Yi－chao，WANG Xi－zhao.Convergent analysis and algorithmic improvement of differential evolution［J］.Journal of Software，2010，21（5）：875－885（in Chinese）.［賀毅朝，王熙照.差分進化的收斂性分析與算法改進［J］.軟件學報，2010，21（5）：875－885.］

［5］GAO Yue－lin，LIU Jun－mei.Dynamic differential evolution algorithm with random mutation［J］.Journal of Computer Applications，2009，29（10）：2719－2722（in Chinese）.［高岳林，劉俊梅.一種帶有隨機變異的動態差分進化算法［J］.計算機應用，2009，29（10）：2719－2722.］

［6］CHI Yuan－cheng，FANG Jie，CAI Guo－biao.Center mutation based differential evolution［J］.Systems Engineering and Electronics，2010，32（5）：1105－1108（in Chinese）.［池元成，方杰，蔡國飆.中心變異差分進化算法［J］.系統工程與電子技術，2010，32（5）：1105－1108.］

［7］Storn R，Price K.Differential evolution－a simple and efficient heuristic for global optimization over continuous spaces［J］.Journal of Global Optimization，1997，11（4）：341－359.

［8］YANG Qi－wen，CAI Liang，XUE Yuancan.A survey of differential evolution algorithms［J］.Pattern Recognition and Artificial Intelligence，2008，21（4）：506－513（in Chinese）.［楊啟文，蔡亮，薛云燦.差分進化算法綜述［J］.模式識別與人工智能，2008，21（4）：506－513.］

［9］Noman N，Iba H.Enhancing differential evolution performance with local search for high dimensional function optimization［C］.Beyer HG，et al.Proc of the Conf on Genetic and Evolutionary Computation.New York：ACM Press，2005：967－974.

［10］Zhang Jun，Hu Xiaomin，Tan X.Implementation of an ant colony optimization technique for job shop scheduling problem［J］.Transactions of the Institute of Measurement and Control，2006，28（1）：93－108.

［11］Cai Zhaoquan，Huang Han.Ant colony optimization algorithm based on adaptive weight and volatility parameters［C］.Shanghai：IEEE Press，2008：75－79.

［12］Li Yancang，Li Wanqing.Adaptive ant colony optimization algorithm based on Information entropy［J］.Foundation and Application，Fundamental Informaticae，2007，77（3）：229－242.

［13］XIAO Jing，LI Liang－ping.Adaptive ant colony algorithm based on information entropy［J］.Computer Engineering and Design，2010，31（22）：4873－4876（in Chinese）.［肖菁，李亮平.基于信息熵調整的自適應蟻群算法［J］.計算機工程與設計，2010，31（22）：4873－4876.］

［14］DENG Ze－xi，LIU Xiao－Ji.Chaotic mutation differential evolution algorithm combined with niche［J］.Computer Engineering and Applications，2010，46（25）：31－33（in Chinese）.［鄧澤喜，劉曉冀.基于小生境的混沌變異差分進化算法［J］.計算機工程與應用，2010，46（25）：31－33.］

［15］Tseng Lin－Yu，Chen Chun.Multiple trajectory search for large scale global optimization［C］.IEEE Congress on Evolutionary Computation，2008：3052－3059.