水作為制冷劑的透平冷水機組研究現狀 (三)

周子成

4 第三部分

壓縮水蒸汽的透平壓縮機葉輪設計

雖然水是最古老的制冷劑之一,它已經在吸收式冷水機組和蒸氣噴射的壓縮式冷水機組中應用了很多年。然而,它應用在透平壓縮機的壓縮式制冷裝置中具有更高的能效。這種裝置的成功應用僅只是最近幾年的事。

水是一種自然制冷劑。水作為制冷劑在透平壓縮機制冷裝置中應用具有以下一些特點:由于循環處在真空下工作,水蒸汽的容積制冷量非常小,因而需要很大的容積流量,需要用相當高的壓比去壓縮它。因此,與傳統的制冷劑如R134a或R12相比,在相同的使用條件下,用水 (R718)作制冷劑造成近200倍的高容積流量和雙倍的壓縮比。由于水蒸汽的這種熱力學性質,對于葉輪設計,這一高壓比通常要求圓周速度比常規葉輪高2至4倍,而聲速是接近高2.5倍;雷諾數低約300分之一;單位質量的傳遞功約高15倍。高性能的混流式透平壓縮機適合于這樣的工作條件。

為了獲得高壓比,這種壓縮機需要用高轉速和大直徑的葉輪。葉輪直徑的上限主要是受使用空間和制造設備的限制。當壓縮水蒸汽時,葉片頂尖速度通常是受轉子穩定性的限制,而不是受聲速的限制。在真空條件下工作時,葉片受到的氣體力非常小,因此,葉片所承受的主要是由質量慣性引起的非常大的離心力,故需要采用輕質葉片,大多數是由鈦或合成材料制成的特別薄的直葉片。這種葉片不能磨,通常它們由幾部分組成,并且它們與常規的高性能葉輪不同。

由于葉片角統一成90度,為了防止高的入射氣流引起的沖擊損失,需要采用導向葉片。最簡單的解決方法是使用一個定子,但這樣會帶來使轉子傳遞功減小的缺點。采用一個安裝在同一軸上的曲線葉片導流器會產生較高的傳遞功。通常它的直徑較小,葉片頂尖速度不會達到目前高強度材料的極限速度。因此,為了獲得更高的傳遞功,導流器可以與主軸分成兩體,采用獨立驅動、具有受穩定條件允許的或考慮受馬赫數限制的更高的轉速。

在本文中,將導流器稱為預葉輪,而將混流葉輪稱為主葉輪。兩個葉輪繞同一方向旋轉,它們之間沒有導向葉片。由于高的離心力和工藝上的原因,兩個葉輪都采用徑向直葉片 (圖3.1)。

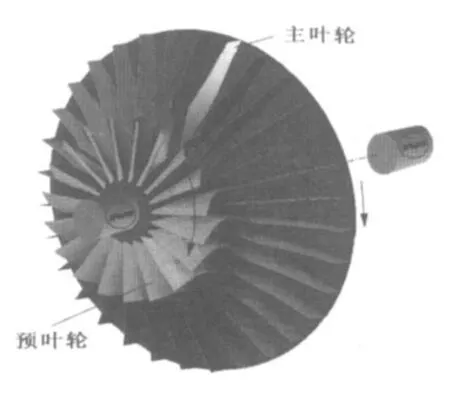
圖3.1 預葉輪和主葉輪

徑向直葉片旋轉起來像一個堅實的固體,因而常規的自由渦流設計方法不適用于這種葉輪。在本設計方法中,初步設計階段是采用一個快速準三元流動算法,并引入這一系統的流動計算。通過一個設計例子,說明這一系統可實現合理的設計,包括對這一系統徑線葉片穩定流動的研究。并且,由于需要高壓比,采用了按照平均流線模型的歐拉方程導出的最大傳遞功的設計法則。

Müller[3.1]提出了一種具有預葉輪和主葉輪的壓縮水蒸汽的壓縮機系統的設計方法。它給出一個快速設計和一個包含由預葉輪和主葉輪組成的葉輪對的氣體流動計算算法。預葉輪是曲葉片的軸向流,主葉輪是完全直葉片的混合流。該計算方法限于徑線葉片的葉輪,通常由于高傳輸功、高容積流量和(或)穩定性和工藝等原因,適用于設計在真空條件下壓縮高壓比的水蒸汽、用水作為制冷劑的離心式制冷裝置。

4.1 徑線葉片

為了對主葉輪的完全直葉片產生必要的預旋,將預葉輪的葉片做成曲面。預葉輪葉片的型線是由一個在參考半徑rR上給定的弧線決定。因為使用徑線葉片,由圓弧rR形成弧形線。如圖3.2。這種葉片非常適合于速度接近聲速和低雷諾數。

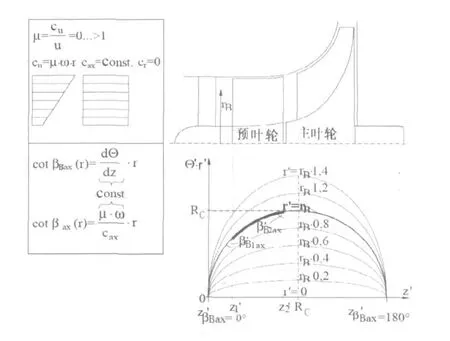
圖3.2 徑線葉片

給定葉片引導邊和尾邊的軸向葉片角β′Bax1(rR)、 β′Bax2(rR)預葉輪軸向長度L′ax=z′2-z′1后,在rR處的弧線就可確定:

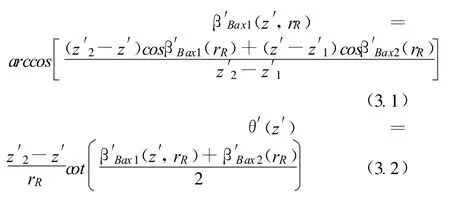
用徑線葉片 β′Bax1(z′,rR)確定在任何位置(z′,rR)的 β′Bax1(z′,r′),并且,如果在rR處的弧線不是圓弧,則

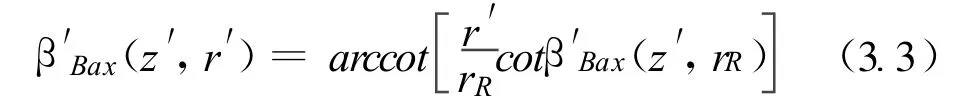
如果在半徑rR處的弧線是一個半徑為Rc的圓弧,則它在所有其他半徑r′處是在z方向具有半軸Rc的橢圓圓弧。它在θ方向r′＜rR處的半軸是Rc,而在r′＞rR處的半軸是恒大于Rc(圖3.2)。它取決于專門設計的β′Bax1(rR)＞0和 β′Bax2(rR)＜180°,只有一段弧線適合于葉片。

此外,流動角符合公式 (3.3),取決于假設的一個固體旋渦分布和軸向流cm(r)=定值 (見圖3.2左側)。因此,β(rR)=βB(rR),且對于在任何半徑r≠rR時,β(r)=βB(r)也是正確的。如果一旦引導邊和尾邊的流動和葉片角一致,將此關系應用于預葉輪,參考半徑rR的變化將不改變這種一致的關系。但是它將會改變它的導數關系?β′B/?r′和?β′B/?z′,因此,改變rR將意味著改變葉片上的負荷分布 (圖3.3)。

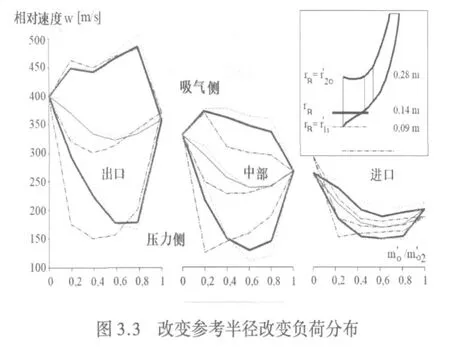
預葉輪的葉片厚度是由在外徑的厚度δ′bo和向內厚度增量dδ′bo/dr決定。主葉輪的葉片厚度 δB保持定值。

4.2 算法

本算法是計算預葉輪和主葉輪及非設計點流量的快速設計計算方法,它適用于亞聲速的葉輪。但在跨聲速和超聲速也是穩定的,不過在超聲速時忽略了沖擊。依靠引入效率系數確定該兩個葉輪由于粘性、流動脫離、入射、超聲速沖擊損失等因素的影響。

本算法 (圖3.4)主要是建立在力的簡單平衡和滿足連續性方程的基礎上 (圖3.5)。在這個準三元計算程序中,葉片到葉片的流動計算是一個兩元直通流動的疊加,以便獲得葉片上的速度分布。預葉輪葉片的幾何成形是聯接到流動計算中,它導致兩個葉輪的合適關聯。

圖3.5 程序算法

4.2.1 力的簡單平衡

考慮了下列幾種力的平衡:(1)由于流體圓周速度分量的徑向力;(2)由于流體子午流線曲率和子午流速分量的離心力;(3)由于壓力梯度的壓力力;(4)施加在流體上的葉片力。平衡是按照圖3.5中沿著n的方向。

在預葉輪區,葉片是曲面,n方向是徑向,其他無葉片或葉片具有恒定的90°的地方,n方向可以是任意方向,結果是,葉片力是零或在n方向沒有分量,因為葉片力是垂直于葉片表面,即使用徑線葉片時,力是在圓周方向。

當cu(n)和hτ(n)已知時,式 (3.4)應用于無葉區,假設在那里的角動量是定值。對于已知氣流角 β(n),用 ωr(n)-cotβ(n)cm(n)代替cu(n)。考慮到cos(εn)=?r(n)/?n,得出式 (3.5),該式應用于大多數葉輪區域。

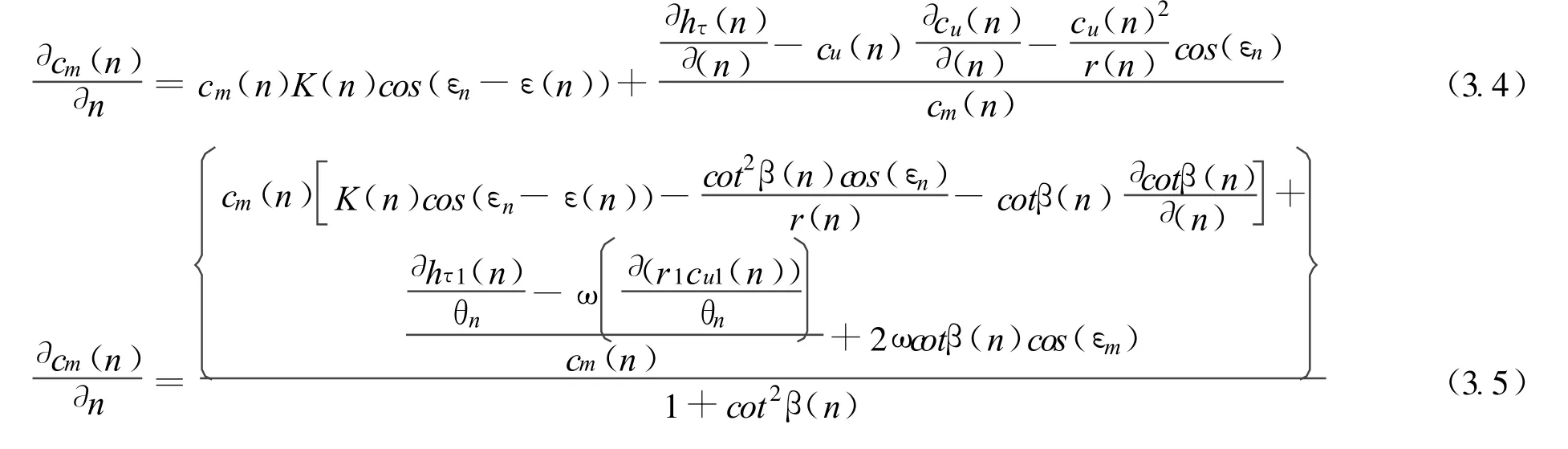
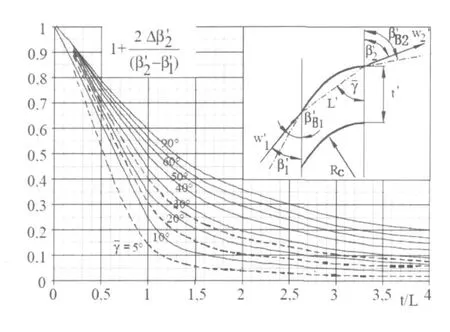
圖3.6 偏離角:按照weining(1935)的擴張系數

4.2.2 主葉輪出口的偏離系數

混流式葉輪出口 (該處氣流出口角開始與葉片角偏離)的斯坦尼茲半徑,由Stanitz和 Prian(1951)給出如式 (3.6)

由于主葉輪的葉片具有90°的恒定葉片角,在這里的偏離系數被定義為 μ=cu/u,對于 βB2=90°,按照Busemann(1928)的結果和Trauple的推薦,采用式 (3.7)作為預測值:

μ2,N=16=0.85 適用于D1/D2≤0.65

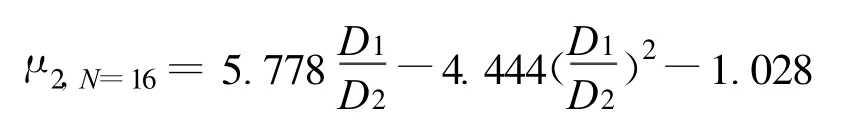
適用于D1/D2＞0.65 (3.7)

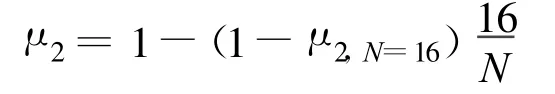
在rs＜r＜r2區域,μ(r)是一個兩次方的公式,并且在式 (3.8)中 βB=常量=90°。

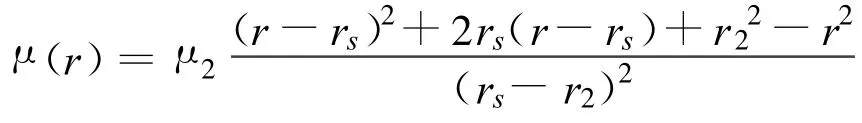
適用于rs＜r＜r2(3.8)

表3.1 必要的輸入數據

Müller(1999)曾表示,公式 (3.8)是當量于sin(β(r))的兩次方公式 (Stanitz和Prian 1951)或 βB=常量 =90°時的cos(β(r))。這里,作為近似選擇,cu(r)直接是U(r)。因此,計算時不依賴于子午分量,以便簡化算法,并且公式 (3.4)可以用于rs≤r≤r2區域。

4.2.3 預葉輪出口偏轉角

預葉輪出口必要的葉片擴張角 △β′2是按照Weining(1935)和Teaupel(1988)從數字化作圖的預測作為建議值,如圖3.6所示。按照Teaupel(1988),如果葉片沒有精確的弧形型面,這種計算會獲得非常好的結果。

4.2.4 預葉輪進口入射角

按照Weining(1935),最佳入射角等于葉輪出口的偏轉角。因此,建議入射角為l′=-△β′2,對于使用徑線葉片,它只是在一個半徑上給出。由于在外半徑處發生最大的傳遞功,它給出在外半徑上。

4.2.5 主葉輪進口入射角

按照Lieblein,對 β1=90°最佳入射角為正值,并且接近于零。按照Wennerstern(1965)考慮到可壓縮性,β2-β1≈0。對馬赫數Mw1≈0.7,該值從 2°到3°變化,因此默認出口半徑處采用入射角lo=0。

4.2.6 程序編碼

圖3.4表示了程序編碼的流程圖。

(1)輸入:為了減輕設計者的工作量,對于初始設計預葉輪和主葉輪的匹配,算法要求盡可能少的輸入數據 (見表3.1)。設計者可以按照他們自己的判斷,改變任選輸入數據的默認值 (表3.2),作多種變化的設計。

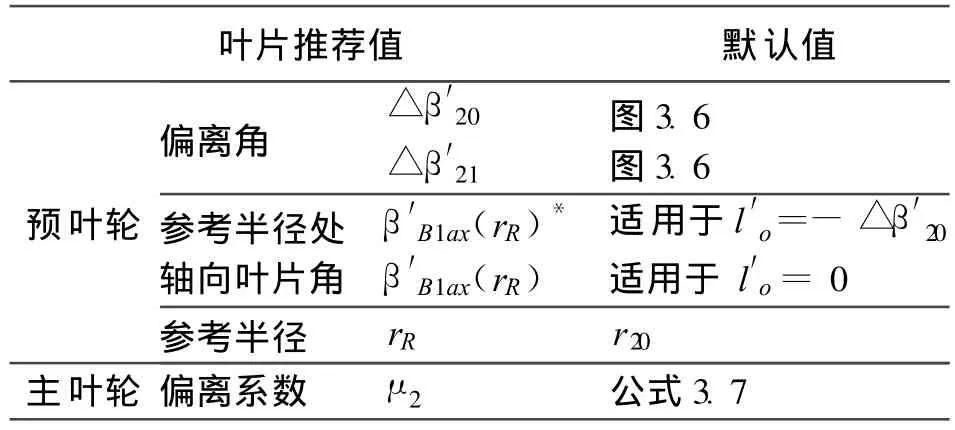
表3.2 任選的輸入數據

(2)子午面輪廓:子午面輪廓是一種在內、外直徑上插值的貝塞爾(Bezier)曲線(Farin 1993)。它是在兩個葉輪內、外直徑的引入邊和尾邊輸入坐標(z,D)的結果。Bezier曲線確定坐標 (z,r)以及在內、外徑每一處的傾斜角ε(m)和曲率K(m)。

(3)計算網格:從引入邊至尾邊將曲線分區,如同主葉輪部分中的斯坦尼茲 (Stanitz)半徑那樣,然后,將主葉輪區域上的曲線段再等分成等長度的參數段,在預葉輪和兩葉輪之間,將曲線細分成相等的軸向長度。連接內、外直徑上相同數量的點之間的線并作為n方向的計算網格。m網格—子午面流線—連接n網格線上相同數量的點。對于第一次計算,M網格線的間距是定值。△n=定值。

(4)子午面流速:沿著每一n網格線和通過流動分量Cm(m,n),對充滿整個場用隆格庫塔法解出公式 (3.4)和式 (3.5)的Cm(n)。對這個初值,Cm(n0)初值取作疊代值,直到積分與所需的質量流量值相符合。對于第一次的演算值,一個n方向的線性插值給出了曲率值K(n)和流線的傾斜角ε(n)的值。對于下一個演算值,K(n)和ε(n)由步驟(5)得出結果。

第一個Cm(n)是用式 (3.4)計算出預葉輪進口的值,并假設無旋渦流動C′u1=0。第二個Cm(n)是用式 (3.5)計算預葉輪出口的值,β′2o的結果由C′m2o和C′u2o得出。其中C′u2o的結果由lo=0假設葉輪之間恒定的角動量C′u2o=Cu1r1o/r′2o得出。葉片角 β′B2o按照 △β′2o和ε′2o得出 。以及 β′B2axo是由式 (3.3)的 β′B2ax(rR)得出。類似地, β′B1ax(rR)根據 △β′1o、ε′1o和l′o=0 得出。因此,預葉輪葉片的形狀由式 (3.1)至(3.3)建立。現在,固定 β′B1ax(rR)和 β′B2ax(rR),從預葉輪的進口重新開始計算,并且通過每n個網格在葉輪前和后的無葉區,以及在主葉輪的r＞rs區解出方程 (3.4)。葉輪的其他區域用公式(3.5)解出。

(5)流線:已知流場Cm(m,n)的流線間隔,用它們之間的等質量流量校正,它改變沿n網線的網格點的坐標(z,r)。現在,采用四階B-樣條插值代表這些流線的新點,并且給出當地曲率值K(m,n)和傾斜角ε(m,n),在n方向的這些值,與它的最初值和它的后一代遺傳值的加權平均值,給出了非常自然的分布和有助于非常快的算法轉換。內徑和外徑上的這些值保持不變。

(6)子午面速度:用這些K(m,n)和ε(m,n)的更新值修正網格,重復步驟4得到這些連續的值。通過選擇重復步驟5和6,進一步變換結果,但對于初步設計是不需要的,因為變化通常是非常小。

(7)葉片上的相對速度:計算葉片上的相對速度回到Stanitz和Prian(1951)的理念,并表示成式(3.9)。

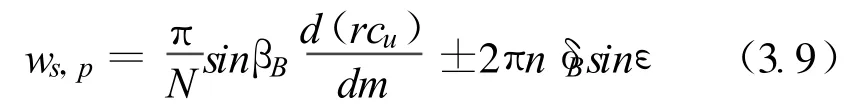
(8)輸出:改變一個輸入值,運行整個程序和產生一個完整的初始結果,輸出是數字和圖形。

4.2.7 關閉設計點

葉片角 β′B1ax(rR)和 β′B2ax(rR)可以被固定,它圍繞葉片在步驟 (4)中產生,變化葉尖速度、容積流量或者吸氣壓力和溫度,然后模擬關閉設計點。輸入值 η′,η,△β′20,△β′21和 μ可以按照設計者的判斷同時調整。

4.3 設計示例

一個設計示例 (圖3.7)表示了帶徑線葉片的預葉輪和主葉輪的合理設計是可能的。得到了一個高流量密度和流速接近聲速的緊湊系統的預期的高壓比結果。示例的結果與實際經驗相符。

工作流體是處在真空條件下的水蒸汽。主葉輪的頂尖直徑是1m(39.37in)。最大頂尖速度不允許超過500m/s(1640ft/s),最高rpm時的吸氣容積流量假設是30m3/s(1640ft3/s)。兩個葉輪的效率假設是70%。還有,需要一個沒有不穩定的流動的寬容積流量的工作范圍。相對速度的減速比應該是可接受的。

圖3.7的右邊部分表示了設計例子的子午輪廓。圖3.7的左邊部分表示了葉片上的相對速度。這些相對速度的減速比列于表3.3。由于運轉范圍內的低雷諾數,所有相對速度減速比均限制在一定安全裕度范圍內。因此預期沒有流動脫離。

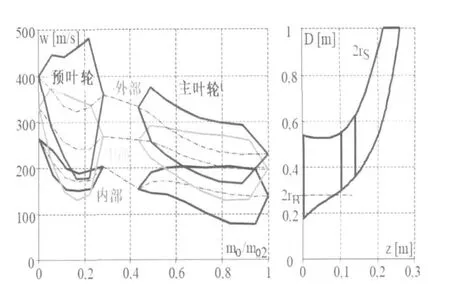
圖3.7 設計例子

表3.3 相對速度的減速比

W曲線的寬廣形狀相應于Dallenbach(1961)準則。預葉輪外徑的當地頂尖值是容許的。因為它們在靠近外徑的下一流線中趨于零 (圖3.7上未表示出)。這種典型的設計在預葉輪的外徑是高負荷,并且在主葉輪具有相對均勻的負荷分布。

圖3.3表示負荷隨參考半徑rR變化而變化的分布。大的rR傳遞更多的負荷。然而,對于大的變化,子午輪廓必須變化。

設計示例的工作范圍是處在30至20m3/s(1060至705ft3/s)的范圍內。由圖3.8右邊部分的實線表示。細實線表示在那里發生完全堵塞,而粗虛線V′max(M*max)表示在那里設定的馬赫數在絕對坐標系統限制在1.3,在相對坐標系統限制在1。點線內輪廓Cl(M*max)(圖3.8左邊部分)粗略表示輪廓可以狹窄到什麼范圍,直到馬赫數達到限制值。在容積流量小于最小流量V′max時,由于力的平衡使不穩定發生。低于最小必須流量的因素是:(1)在內徑較低的曲率,(2)在外徑較高的曲率,和 (3)較高的輪廓頂尖比 (hubtip ratio)。

圖3.8 流動穩定和容積流量

4.4 穩定流動

圖3.8也表示了延伸到不穩定流動的效果。對于這種目的,示例中的輪廓頂尖比是描述為更低的內徑 (圖8中的虛線輪廓),導致在力平衡關系中的不平衡。因此,這區域被認為是流動從輪廓脫離的尾渦區域。這一區域是由內徑和力平衡Clmin需要的一個最小直徑的內輪廓所包圍。

Müller(1999)進一步研究了不穩定的物理背景,由于在外半徑處有更高的總焓,導致在那里有更高的全壓力。為了補償這個從外徑到內徑的梯度,需要一個高梯度的子午速度去控制當地壓力。高的圓周速度也有利于補償高的旋渦比 μ。但是如果在外徑的子午速度不足夠高,內徑以上的子午速度達到零。負的子午速度值 (回流)不能求解這一問題,因為它們低于當地壓力,與增加正值的方法一樣。因此,力不能被平衡。

Müller(1999)使用了一個模型。假設在管道內有一固體漩渦分布的軸向流, 以及全焓的當量分布ht(r)=ht1(r)+cu(r)ωr,這個簡單的徑向力平衡的閉合解,給出了在外徑處相對于cmo的分布cm(r):

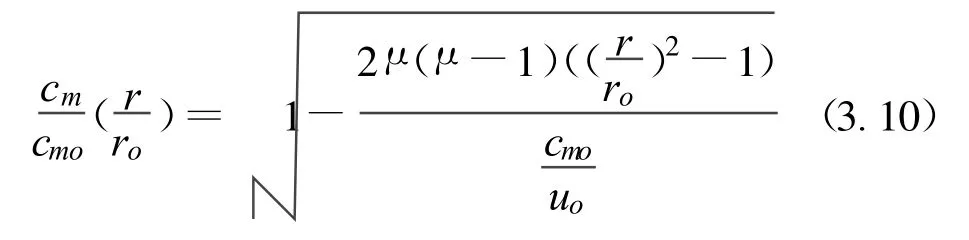
對于比值r/ro＜(r1/ro)min僅發生在μ＜1,且＜0.707。沒有真實解;cm在(r1/ro)min達到零。最小比值(r1/ro)min—作為輪廓頂尖比的插值—表示于Müller(1999)的著作中。當渦旋比為0.5時,它們達到最大值。大多數情況下,它是在預葉輪的一半路程上。但壓縮機中的流線曲率和傾斜角是從臨界區移向主葉輪進口。

4.5 設計規則

Müller(1999)將歐拉方程應用于平均流線模型和替代參數導出了設計規則,這樣,剩下的只是選擇設計參數。

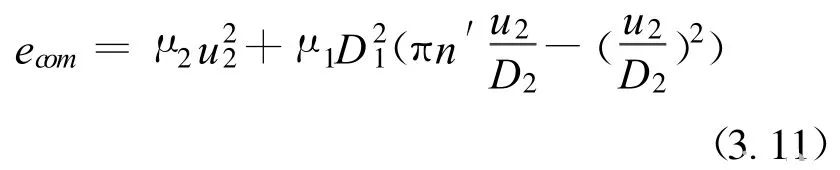
公式(3.11)的估算容易地表明,在這樣的設計中最大功的傳遞是相應于:(1)頂尖速度u2,和(2)主葉輪進口直徑D1和(3)預葉輪轉速n′應選擇最大值。同樣的設計規則對(4)偏離系數 μ2和(5)主葉輪預旋系數 μ1也是正確的,但是通常計算機沒有這麼多存貯空間去調用這些參數,(6)還有,如果預旋比 μ1=1或者是n′/n=1+μ1,主葉輪轉速應是預葉輪的兩倍。Müller(1999)也給出了在最高吸氣容積流量下不超過給定極限馬赫數時,最佳預葉輪進口直徑的近似關系:

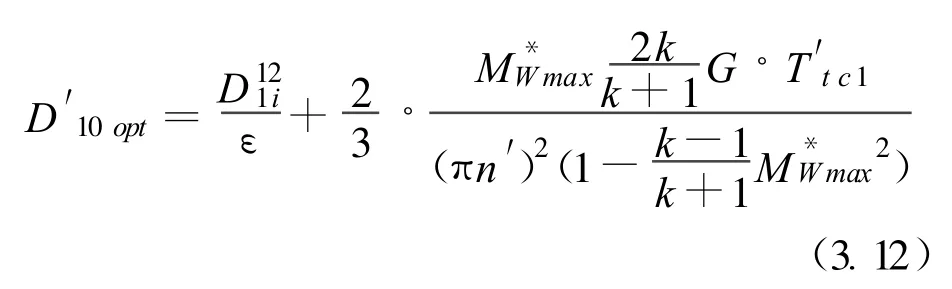
在同樣的研究中,Müller表明用一個預葉輪代替一個導流器,功的傳遞可以增加15至40%,而用一個預葉輪代替定子,功的傳遞可以增加40至120%,主要取決于D1/D2。D1/D2的低值是0.4,高值是0.6。

4.6 CDF技術

文獻 [3.2]論述了一個專門為大容量空調設備開發的以水為制冷劑的高效兩級離心壓縮機。它只采用主葉輪,沒有預葉輪,替代預葉輪功能的是固定進口導葉。透平冷水機組的COP(性能系數)目標值是超過6.0,制冷量大于3517kW(1000美國冷噸)的COP目標值是6.4,這是透平冷水機組中最高的COP,制冷量2462kW(700美國冷噸)的COP達到6.3。為了滿足這樣的高COP值,需要開發效率比傳統的離心式壓縮機高得多的新型離心式壓縮機。這種R718離心壓縮機的葉輪設計與常規設計不同。

在壓縮機的新設計中成功地應用了CFD技術,即計算流體動力學技術。CFD是英文Computational Fluid Dynamics(計算流體動力學)的簡稱。它是伴隨著計算機技術、數值計算技術的發展而發展起來的。簡單地說,CFD相當于 “虛擬”地在計算機中做實驗,用來模擬仿真流體的實際流動情況。其基本原理是數值求解控制流體流動的微分方程,得出流體流動的流場在連續區域上的離散分布,從而近似模擬流體的流動情況。因此,CFD是一種現代模擬仿真技術,已成為解決分析工程問題的有力工具。

第一級壓縮機需要一個寬的穩定運轉范圍,以便容易與第二級壓縮機相匹配。熱力循環的分析表明,第二級壓縮機有一個高負荷 (高壓力系數)。

利用葉片重新定向流動進入葉片的旋轉方向增加葉輪的壓力 (見圖3.9)。當依靠改變葉片的有限厚度改變流動方向時,吸氣側流速變得更高 (壓力變得更低)和壓力側的流速變得更低 (壓力變得更高)。當葉片變得更厚時,吸氣側和壓力側之間的速度差 (壓力側和吸氣側之間的壓力差)變得更大。為了實現一個更大的壓力提升,吸氣側和壓力側之間的速度差 (壓力側和吸氣側之間的壓力差)變大。在葉輪出口,壓力側和吸氣側具有相同的速度(壓力)。這導致在吸氣側迅速減速 (逆壓力梯度),造成分離和損失。確保穩定運行范圍和更高效率的關鍵之一是降低作用于第一和第二級的壓縮機每個葉輪葉片的載荷 (壓力側和吸氣側之間的壓力差)。因此,采用減少第一和第二級的葉輪的葉片厚度,并增加了葉片數。還通過增加導流罩側上游的傾斜度使分離葉片 (短葉片)的長度增加。

為了增加第一級葉輪穩定運行范圍,增加了葉輪出口葉片角 (后彎角)。

為了改善葉輪內部的流動模式,改變了從第一級到第二級葉輪葉片導流邊的形狀,從圓弧變成橢圓,以便抑止葉片導流邊的突然加速/減速 (見圖3.9)。還采用一種長葉片和短葉片交替的形狀,使氣流在長葉片和短葉片之間平穩流動。

通過計算流量優化葉片形狀,在第一和第二級葉輪應用計算流體動力學模型 (CFD)對葉輪內部進行流動的數值模擬。

圖3.10表示了傳統的和新設計的第一和第二級葉輪形狀。

作為CFD計算的一個例子,圖3.11表示了導流罩側面的第二級 (跨度85%的位置)葉輪的傳統類型和新類型的相對馬赫數。在常規型的整葉片和分離葉片 (短葉片)的前緣發生輕微分離,而新型葉片在這些地區沒有發生分離。圖3.12表示了采用CFD估算的新類型和常規型葉輪的性能比較。新型葉輪的效率高于常規型。圖3.13表示了第一級壓縮機的性能 (CFD與試驗結果比較)。

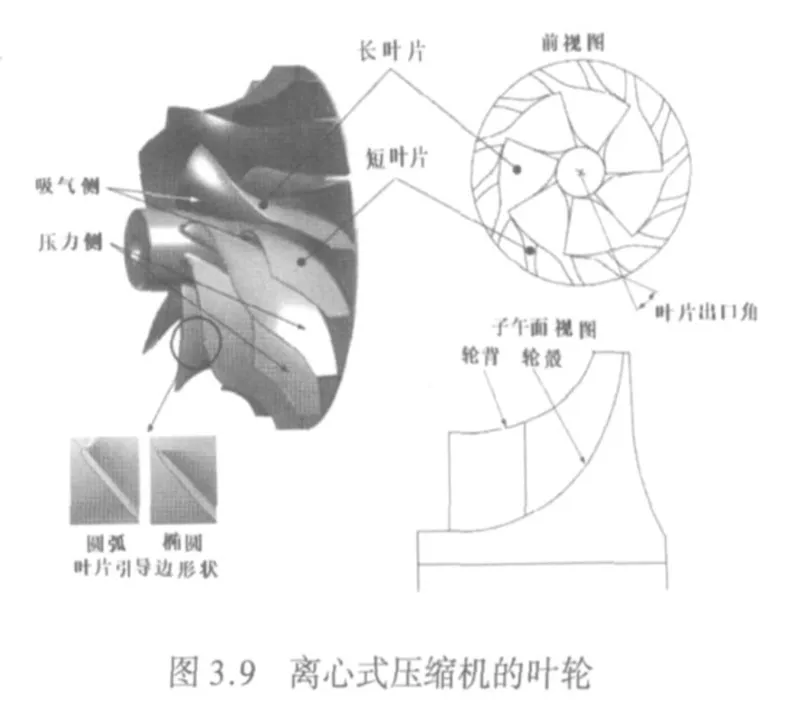
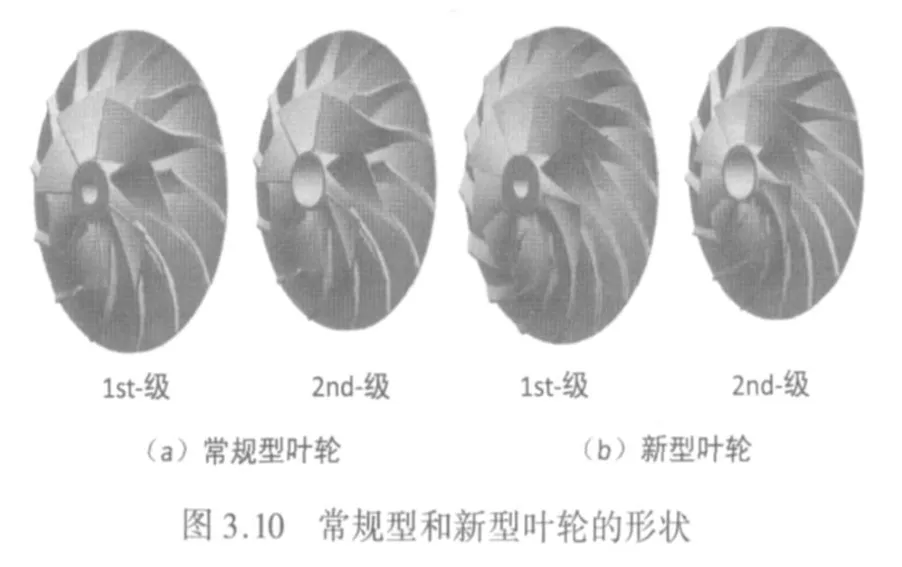
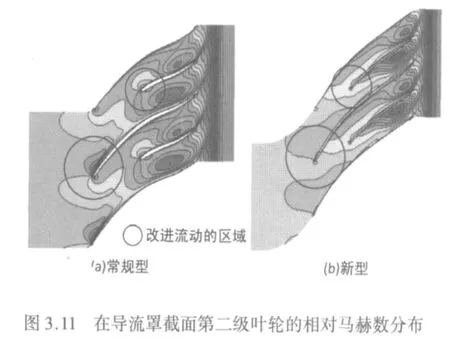
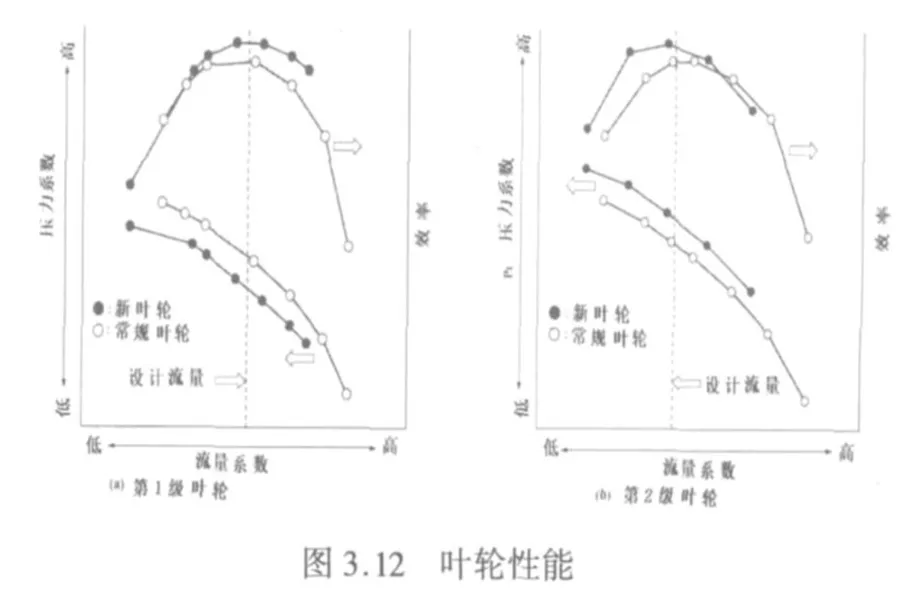
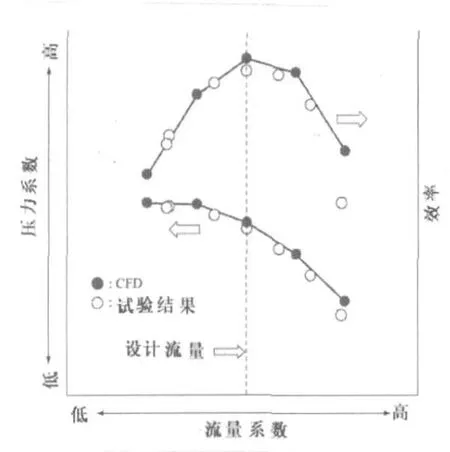
圖3.13 第1級壓縮機性能(CFD與試驗結果比較)

4.7 本部分小結

以上所介紹的計算機編程算法,是對于分別驅動的預葉輪和主葉輪壓縮機的一個完整初步設計的閉合過程。但是,它的前提是假設效率系數保持不變,且必須由設計者的合理判斷來控制。這一算法也適用于跨聲速區,但必須強調指出,它不考慮跨聲速的沖擊。這一算法的優點是它的強大性、快速、通用、簡單和容易使用,該算法適用于徑線葉片的任何包括軸流、混流、和徑流葉輪和固定導向葉片的系統,只要它們限于徑線葉片。式 (3.4)和 (3.5)的使用范圍也容易地包括了預葉輪之前的區域和主葉輪以后的區域。它可以用于在使用現在流行的CFD葉輪分析編碼之前作一個初步階段的設計,以節省許多時間。

應用CFD技術進行壓縮機流道設計,可以對葉輪內部進行流動的數值模擬。分析流道中有無旋渦和脫離現象,改進和優化葉片形狀,提高壓縮機效率。

符號:

C-絕對速度,m/s

D-直徑,m

Df-擴散系數

e-比軸功率,J/kg

G-氣體常數,J/kgK

h-比焓,J/kg

K-曲率,m-1

L-線性長度,m

Lax-軸向長度,m

M-子午方向坐標,m

m-質量流量,kg/s

M*-臨界馬赫數

n-轉速,s-1

n-坐標的n方向,m

N-葉片數

P-壓力,Pa

r-半徑,m

rR-參考半徑,m

rs-斯坦尼茲半徑,(公式3.6),m

t-節距,m

T-溫度,K

u-葉輪圓周速度,m/s

V-容積流量,m3/s

w-相對速度,m/s

z-坐標的軸向,m

a-絕對系統的氣流角,°

β-相對系統的氣流角,°

γ-錯角,從圓周方向測量的角,°

△-差值

δ-葉片厚度,m

ε-傾斜角,°

εn-n方向的傾斜角,°

η-效率系數

l-入射角,°

k-等熵指數

μ-渦旋比 (偏離系數),cu/u

μ2-葉片出口偏離系數,這里對β=90°定義為cu/u

θ-圓周方向角,°

ρ-密度,kg/m3

ω-角速度,s-1

下標:

ax-速度的軸向分量;從軸向測量(不從子午方向測量)

B-葉片

c-絕對系統

C-圓

com-聯合(預葉輪和主葉輪在一起)

i-內徑,m

o-外徑,m

opt-最佳

m-速度在m方向 (子午方向)的分量

max-最大

min-最小

r-速度在徑向的分量

s-葉片吸氣側

t-全值 (在滯止點測量)

u-速度在圓周方向的分量

w-在相對系統

1-進口

2-出口

上標:

′-預葉輪

[3.1]Noebert Müller Desugn of compressor impellersfor water as a refrigerant,ASHRAE Transaction;Research

[3.2]TAMAKI Hideaki et al.,Development of High-Efficiency Centrifugal Compressor forTurbo Chillerm,IHI Engineering Review Vol.42,No 2,2009

[3.3]Müller,N.1999.Entwurf von Laufradem mit Radialfaserschaufeln für Diagonalverdichter mit getrennt angetriebenen Vorlaufer und Hauptlaufer.Dissertation,Technische Universitat Dresden