軌道車輛抗側滾扭桿系統(tǒng)剛度的影響因素

王亞平，劉文松，郭春杰，聶清明，程海濤，葛 琪

（株洲時代新材料科技股份有限公司，湖南株洲412007）

隨著車輛運行速度的提高，為了避免車輛通過道岔和曲線時出現(xiàn)傾覆，并提高車輛通過曲線時乘客的舒適度，抗側滾扭桿裝置在車輛中得到越來越廣泛的應用。在國內(nèi)的軌道交通領域，抗側滾扭桿裝置主要應用于25T型車輛、城市軌道交通車輛以及CRH動車組車輛。

抗側滾扭桿裝置的系統(tǒng)剛度是其最重要的性能參數(shù)，通過與空氣彈簧系統(tǒng)及其他轉向架彈性部件相關參數(shù)的配合可使得車輛達到最佳的安全、舒適效果。扭桿系統(tǒng)主要由扭桿組件、連桿組件和扭桿支撐座組件3部分組成，其中抗側滾扭桿組件是其核心部件，由扭桿軸和扭轉臂組成（彎扭桿中扭桿軸和扭轉臂一體），其大致結構見圖1。

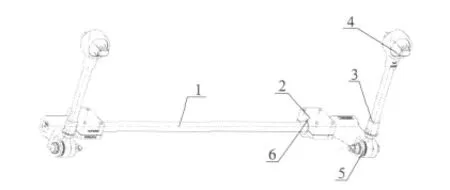
圖1 扭桿系統(tǒng)簡圖

文中符號及定義見表1。

1 扭桿的系統(tǒng)剛度

扭桿的系統(tǒng)剛度是衡量車體在側滾時，扭桿系統(tǒng)能提供側滾阻力的大小，扭桿的系統(tǒng)剛度越小，則在同樣的車體變形的情況下提供的側滾阻力越小，其具體的定義為車體的阻力矩與車體側滾角的變化率。

如圖2所示為車體側滾時扭桿系統(tǒng)的位置變化，其中α為車體的側滾角度，β為扭轉臂上下擺動的角度，γ則為扭桿軸的扭轉角度，當扭桿的阻力在連桿處為±F時，則其阻力矩Tz的計算如式（1）。

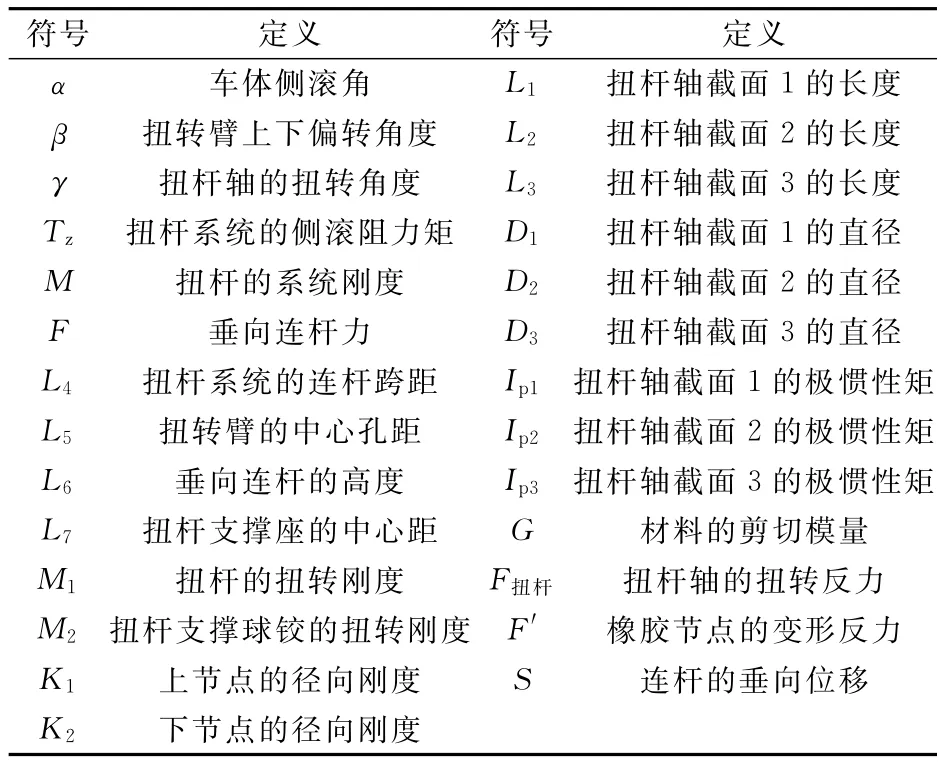
表1 符號及定義

而扭桿的系統(tǒng)剛度M則為，

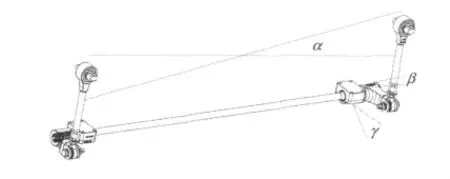
圖2 車體側滾時扭桿位置的變化

扭桿在平衡位置時，左右垂向連桿和扭轉臂在豎直方向上齊平；當車體側滾時，左右連桿在豎直位置上分別向上或向下移動，再通過扭轉臂轉換為扭桿軸的扭轉，此時，扭桿主要通過扭桿軸的扭桿支撐球鉸（內(nèi)支撐時）扭轉變形、連桿組件中的橡膠節(jié)點的徑向壓縮變形提供反作用力，其中金屬部件的彈性變形較小，對扭桿的系統(tǒng)剛度影響可忽略不計。當連桿組件中的節(jié)點采用金屬關節(jié)時，在車體側滾時發(fā)生轉動而非彈性變形，因此對系統(tǒng)剛度影響較小。為了方便計算和理解，引入連桿處的當量剛度KS，其定義為車體側滾時的垂向力與連桿垂向位移的比值。

因此其與扭桿系統(tǒng)剛度的關系為，

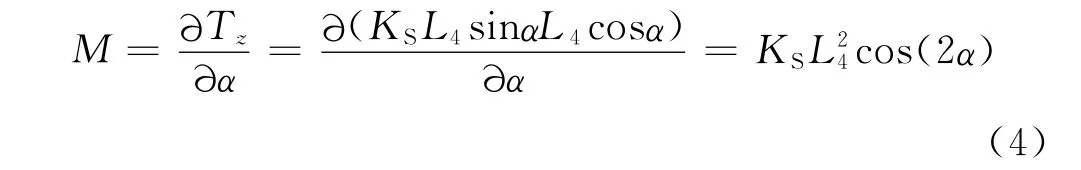
由于車體側滾角通常較小（0～1.5°），因此扭桿系統(tǒng)剛度M與KS的關系可簡化為，

1.1 系統(tǒng)剛度的影響因素

通過對車體側滾過程中扭桿系統(tǒng)變形的分析，可知在車體側滾時，扭桿系統(tǒng)的阻力主要來自扭桿軸和支撐球鉸的扭轉變形、連桿上下橡膠關節(jié)的徑向變形產(chǎn)生的反作用力，因此對扭桿系統(tǒng)剛度的影響分別從扭桿軸、扭桿支撐球鉸、連桿橡膠關節(jié)以及扭桿系統(tǒng)的布局來進行分析。

1.1.1 扭桿軸的結構

扭桿軸的扭轉變形產(chǎn)生的反作用力是扭桿系統(tǒng)阻力矩的主要來源，圖3為典型扭桿軸的結構，常見的扭桿軸按照其扭桿支撐座的位置不同可分為內(nèi)置式和外置式兩種，扭桿軸的3段臺階分別為扭桿軸與扭轉臂、扭桿支撐座的連接部位和扭桿軸的主要受扭截面［2］。內(nèi)置式和外置式扭桿軸的區(qū)別在于扭桿軸與扭轉臂、扭桿支撐座連接部位的不同。

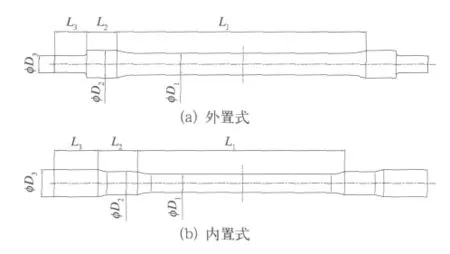
圖3 典型扭桿軸的結構

扭桿軸的扭轉剛度M1由扭桿軸的布局決定，對于結構確定的扭桿系統(tǒng)，扭桿軸的扭轉剛度M1是其固有屬性。

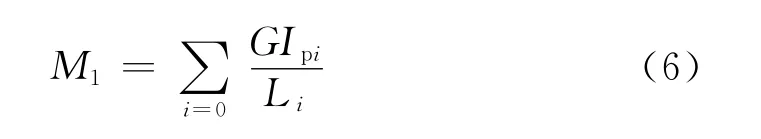
其中Li為在車體側滾時，扭桿軸發(fā)生扭轉變形的部位，對于圖3中的內(nèi)置式，則為L1和L2兩段，而對于外置式的，則為L1、L2和L33段；式（6）中Ip為扭桿軸的極慣性矩，由扭桿軸材料的彈性模量和截面結構確定，對于直徑為D的圓截面，其極慣性矩為，

當車體側滾時，左右連桿的上下位移通過扭轉臂轉換為扭桿軸的扭轉。當連桿的垂向位移為S時，扭桿軸的扭轉角度為γ。

則此時，扭桿軸所產(chǎn)生的扭轉變形反作用力為

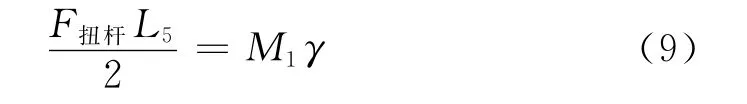
而扭桿軸所產(chǎn)生的扭轉變形反作用力在連桿處的當量剛度為Ks扭桿。

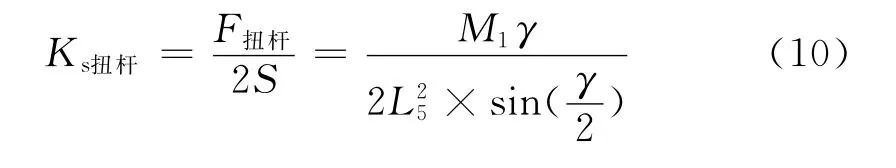
由此可知，扭桿系統(tǒng)在連桿處的當量剛度KS與扭桿軸的扭轉剛度成正比。

1.1.2 扭桿軸的支撐球鉸

當扭桿系統(tǒng)為內(nèi)置式的直扭桿系統(tǒng)時，扭桿支撐座組件與扭桿軸的連接通常采用支撐球鉸的形式，支撐球鉸通常由1至3片的瓦片狀金屬與橡膠硫化在一起，其內(nèi)徑和外徑表面分別與扭桿軸和扭桿支撐座的上下腔體連接，在裝車時，支撐座的上下表面均為過盈連接，在車體側滾，扭桿軸扭轉變形時，扭桿支撐球鉸將隨著扭桿軸一起發(fā)生扭轉變形，因此在考慮扭桿系統(tǒng)剛度M時，需考慮扭桿支撐球鉸的影響。當扭桿系統(tǒng)為外置式時，扭桿軸與扭桿支撐座的連接采用間隙的襯套，在車體側滾時，無變形發(fā)生，因此對扭桿的系統(tǒng)剛度無影響。

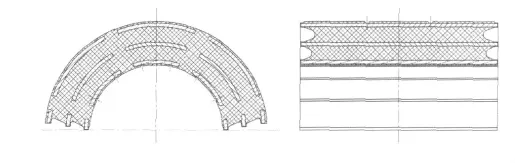
圖4 扭桿支撐球鉸

扭桿支撐球鉸的存在將增加扭桿軸的扭轉變形剛度，扭桿軸與支撐球鉸為并聯(lián)關系，因此其復合剛度M復合為

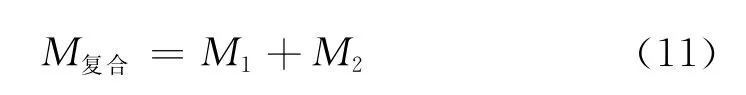
因此，考慮扭桿支撐球鉸作用進行系統(tǒng)剛度計算時，式（10）中的M1應更改為M復合。

1.1.3 連桿的橡膠關節(jié)

在扭桿系統(tǒng)中，連桿上下可采用橡膠關節(jié)或金屬關節(jié)，其中橡膠關節(jié)通過橡膠的壓縮變形來適應側滾時扭桿系統(tǒng)的位置變化，而金屬關節(jié)則通過球面的滑動來實現(xiàn)。橡膠關節(jié)或金屬關節(jié)均可滿足扭桿系統(tǒng)性能的需要，在實際的應用中可根據(jù)具體的工況進行選擇。

當使用橡膠關節(jié)時，車體側滾時，連桿的上、下橡膠關節(jié)首先發(fā)生徑向的壓縮變形，如上下節(jié)點分別選用徑向剛度為K1和K2的橡膠關節(jié)，則扭桿系統(tǒng)在連桿處的當量剛度為Ks。

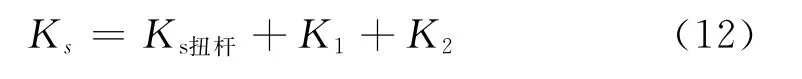
1.1.4 扭桿系統(tǒng)的布局

扭桿系統(tǒng)的布局根據(jù)車輛的設計而不同，除了需考慮扭桿系統(tǒng)的性能需要外，還需與車輛的安裝和運行空間相匹配。通常扭桿系統(tǒng)的部件分別安裝在車體和轉向架上，如圖1所示。扭桿通過連桿組件固定在車體上，再通過扭桿支撐座組件固定在轉向架上（扭桿反裝時安裝位置相反）。

扭桿系統(tǒng)的布局可用連桿跨距L4，扭桿支撐座跨距L7，連桿長度L6，扭轉臂的中心孔距L5，對上述所得到的式（10）、式（11）、式（12）進行綜合考慮，可得扭桿系統(tǒng)剛度M。

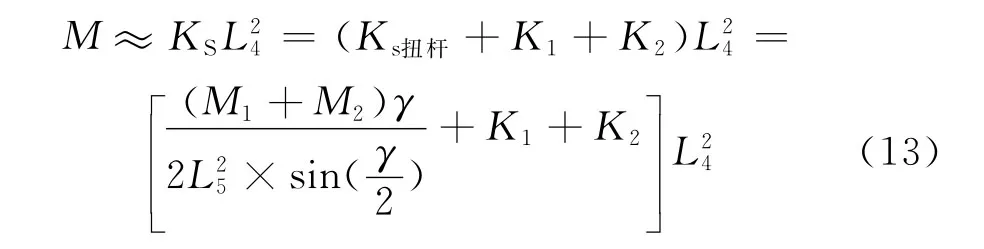
由扭桿系統(tǒng)在車體側滾中的位置變化情況可知，扭桿軸的扭轉角度γ與車體側滾角α的關系：

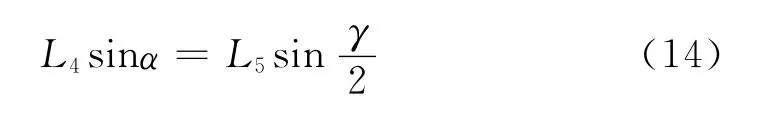
由式（14）可知，扭桿系統(tǒng)布局中僅尺寸連桿跨距L4和扭轉臂的中心孔距L5對扭桿的系統(tǒng)剛度有影響，其中尺寸連桿跨距L4不僅對扭桿系統(tǒng)有直接影響，而且與扭桿軸的長度相關，影響扭桿軸的扭轉剛度，從而影響扭桿的系統(tǒng)剛度。

在扭桿系統(tǒng)中，扭桿軸的扭轉剛度是影響系統(tǒng)剛度的決定性因素，如忽略支撐球鉸、橡膠節(jié)點等其他影響因素，可得到扭桿系統(tǒng)剛度的簡化計算公式為

再將其設想為截面單一的直徑為D，長為L的圓軸，則在其他條件不變的情況下，則

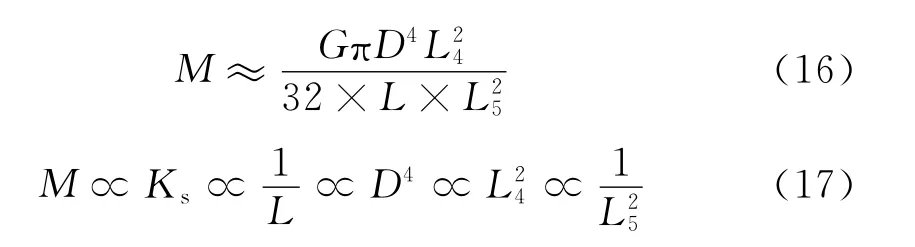
2 系統(tǒng)剛度的滯彈性

圖5為國內(nèi)某鐵路所用扭桿系統(tǒng)的剛度試驗曲線，由圖5可知，扭桿系統(tǒng)剛度的變化呈非線性的變化趨勢，隨著車體側滾角度α的增加，扭桿軸的扭轉角度γ隨之增大，系統(tǒng)剛度也逐漸增大，即扭桿系統(tǒng)提供的側滾反作用力越大。將扭桿的系統(tǒng)剛度曲線分為a、b、c、d4個階段進行分析。

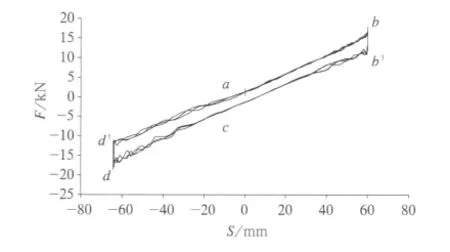
圖5 扭桿系統(tǒng)剛度試驗曲線

首先，在a至b階段，當車體側滾時，車體側滾角度的增大使得連桿的垂向位移也相應的增大，扭桿軸的扭轉角度γ與連桿垂向位移S的關系如式（8），隨著S的增大，單位S增量所引起的扭桿軸的扭轉角度γ將越來越大，即扭桿軸產(chǎn)生的扭轉變形反作用力也越來越大，從而使得扭桿的系統(tǒng)剛度逐步增加；并且連桿的上下橡膠節(jié)點及扭桿支撐球鉸的剛度也是非線性的變化趨勢，即隨著S的增加，式（13）中的M2、K1、K2隨之增大，成為影響a、b階段系統(tǒng)剛度增大的另一因素。

隨后，在扭桿變形的b至c階段，上一階段扭桿系統(tǒng)中的橡膠關節(jié)積累的變形能釋放，使得扭桿系統(tǒng)獲得一個附加的力，相當于垂向連桿力F′，使得車體側滾角的方向變化時，出現(xiàn)了bb＇的剛度曲線的直線突變。且F′在b＇c段有持續(xù)影響。

當扭桿回到平衡位置c后，即開始另一次相同過程的變化，如圖5中的c至a階段。

3 系統(tǒng)剛度的FEA分析

以圖5所顯示的國內(nèi)某鐵路所用扭桿系統(tǒng)進行FEA計算，探討FEA計算系統(tǒng)剛度曲線的方法。采用ABAQUS6.10大型有限元分析軟件進行計算，其中扭桿系統(tǒng)中金屬件采用C3D8R和C3D4混合單元網(wǎng)格、模采用C3D8H單元網(wǎng)格，網(wǎng)格數(shù)量約61 472個。

按照圖6所示進行約束和加載，在點a處設置set，輸出載荷位移曲線。

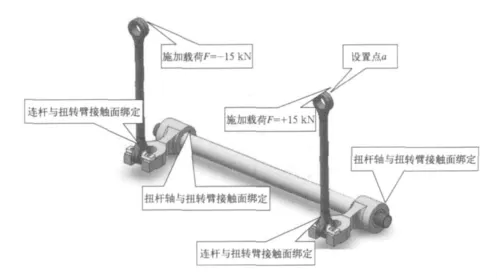
圖6 FEA計算模型

計算結果如圖7，其中包括a點的載荷位移曲線以及扭桿系統(tǒng)的應力云圖。

圖7 FEA計算結果

通過與圖5的試驗剛度曲線進行對比，顯示FEA分析所得到的系統(tǒng)剛度曲線與實際試驗曲線基本重合，但在頂端突變區(qū)域未能取得很好的模擬效果。

4 計算對比分析

將用常規(guī)計算方法、有限元分析方法與產(chǎn)品的試驗得到的扭桿系統(tǒng)剛度進行對比，如表2所示。

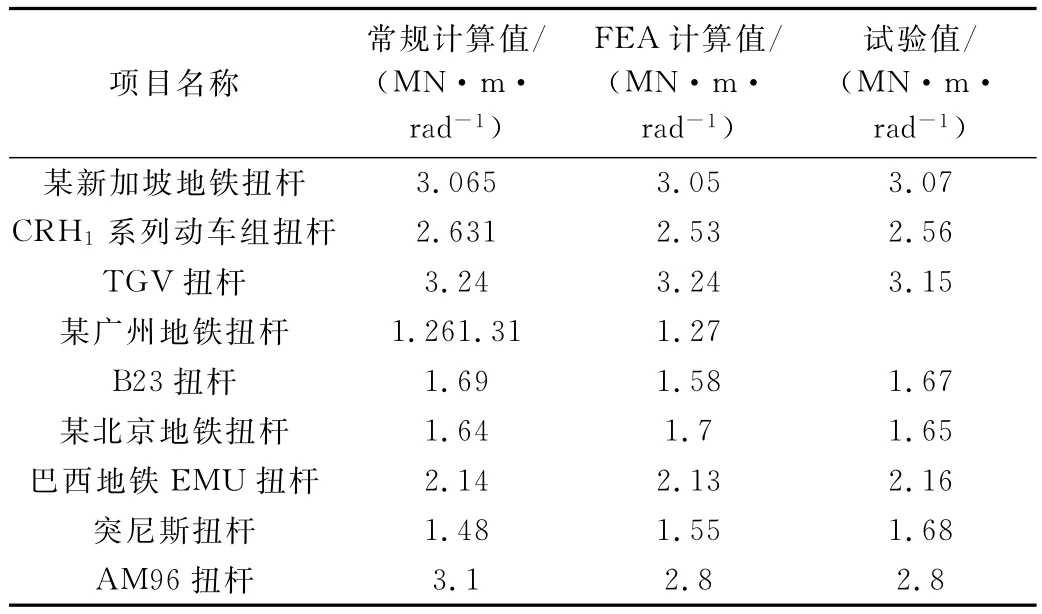
表2 系統(tǒng)剛度計算值對比

經(jīng)對比分析，常規(guī)計算和FEA計算的剛度值與試驗對比均在可信的偏差范圍以內(nèi)（最大不超過±5%）。

5 結論

（1）在車體側滾運行時，扭桿系統(tǒng)的主要變形有扭桿軸的扭轉變形、扭桿支撐球鉸的扭轉變形（內(nèi)支撐式）、連桿上下橡膠節(jié)點以及扭桿系統(tǒng)中金屬部件的彈性變形，因此扭桿系統(tǒng)的系統(tǒng)剛度由扭桿軸的扭轉剛度、扭桿支撐球鉸的扭轉剛度和連桿上下橡膠節(jié)點的徑向剛度決定，其中扭桿軸的扭轉剛度是最主要的影響因素。

（2）扭桿的系統(tǒng)剛度呈非線性，隨著車體的側滾角度變大，扭桿系統(tǒng)的系統(tǒng)剛度隨之增加，其主要原因在于隨著車體側滾角度變大，扭桿軸的扭轉變形變大，扭桿的系統(tǒng)剛度增加以及連桿的上下節(jié)點的橡膠滯彈性也是原因之一。

（3）通過對扭桿系統(tǒng)進行FEA分析，提出了扭桿系統(tǒng)剛度及應力分析的模型，并驗證了扭桿系統(tǒng)剛度的影響因素。

［1］嚴雋耄，傅茂海.車輛工程（第3版）［M］.北京：中國鐵道出版社，2008.

［2］劉文松，郭春杰.符合法鐵標準的抗側滾扭桿軸的工藝研制［J］.鐵道車輛，2007，7（45）10－13.