粘滯阻尼器在金水溝特大橋中的應用研究
周友權
(中鐵第一勘察設計院集團有限公司橋隧處,西安 710043)
1 工程概況
黃韓侯鐵路是連接陜西省黃陵縣與山西省侯馬市的1條客貨共線鐵路,位于鐵路線上的金水溝特大橋,其主橋孔跨布置為(80+3×140+80)m,聯長581.8 m,主橋3、4號主墩為剛構墩,2、5號次主墩及1、6號邊墩為連續梁墩,整體結構為剛構連續梁橋。橋面與地面的最大高程差約93 m,3、4號墩墩高均為80 m,2、5號墩高均為55 m,立面布置如圖1所示。橋址處的地震動峰值加速度值為0.152g,相當于地震基本烈度7度,地震動反應譜特征周期為0.43 s。由于金水溝主橋墩高聯長,屬于技術復雜、修復困難的特殊結構橋梁[1],并且地震動峰值加速度為0.152g,需對全橋進行專門的抗震分析,并采取一定的減震措施。
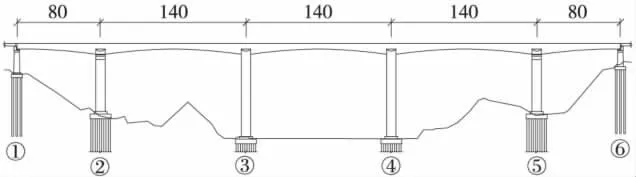
圖1 全橋立面布置(單位:m)
2 主橋抗震分析
2.1 模型建立
采用Midas/Civil 2010程序,將金水溝主橋離散為空間梁單元,用M法計算樁基對承臺的彈性支承剛度,在模型承臺底加上6個自由度的彈性支承,計算模型如圖2所示。
2.2 地震波來源

圖2 計算模型
由于金水溝主橋結構的特殊性,對其橋址區做了專門的地震安全性評價工作。采用擬合基巖反應譜的三角級數迭加法合成場地基巖地震動時程,給出了50年超越概率63%、10%和2%三種設防概率水平的合成場地基巖地震動加速度時程,每種概率水平各給出了3條加速度時程。由于本橋墩高聯長,屬于修復困難的重點橋渡,并且橋址屬于0.15g的7度區,因此擬采用3條超越概率2%的人工合成波來進行全橋的地震反應分析。當采用3條時程波計算時,時程分析的最終結果應取3組計算結果的最大值[2]。圖3僅示出了50年超越概率為2%的1條時程曲線。

圖3 水平地震動時程曲線(2%)
2.3 地震反應結果分析
將50年超越概率為2%的3條時程曲線分別輸入,在Midas中采用直接積分法,得到順橋及橫橋向主橋的地震反應。當采用3條時程波計算時,時程分析的最終結果應取3組計算結果的最大值[2]。將地震力與主力進行組合,按照橋墩與樁基的實際配筋,對樁基的承載力及橋墩樁基的強度進行檢算。橫橋向樁基的承載力及橋墩樁基的強度均滿足要求,這是由于橫橋向由上部結構產生的地震力由2~5號4個主墩分擔。在順橋向,3號與4號主墩樁基承載力及橋墩樁基的強度遠遠超限,而其他橋墩樁基的承載力及強度還有很大的富裕量,這是由于縱橋向由上部結構產生的地震力僅由3號與4號剛構墩來承擔,其余墩主要承擔橋墩自身產生的地震力。另外,查看結構的地震反應發現,地震下連續梁墩墩頂處的梁與墩之間的相對位移很大,最大雙邊位移之和即位移幅值在40 cm左右,地震下梁端伸縮縫與邊墩頂帽高出部分很容易發生破壞。因此,擬在次主墩縱向設置耗能的液體粘滯阻尼器,減小橋梁縱向的地震反應,并使次主墩分擔縱向地震力的比重加大,以確保結構的安全。
3 粘滯阻尼器參數的選取
3.1 粘滯阻尼器的特性
粘滯阻尼器一般由活塞、油缸及節流孔組成,是利用活塞前后壓力差使油流過節流孔產生阻尼力的一種減震裝置[3]。粘滯阻尼器的公式為[4]

式中,F為阻尼力;C為阻尼器的阻尼系數;V為阻尼器兩端間的相對運動速度;α為速度的指數,其取值范圍為0.1~2,從抗震角度,其常用的取值范圍為0.2~0.5。
由粘滯阻尼器的公式可知,在溫度、收縮和徐變等荷載作用下,V值很小,粘滯阻尼器產生的阻尼力很小,對結構產生的附加力也很小[5];在地震作用下,墩梁間的相對速度很大,阻尼器可以對結構提供較大的反力,并且阻尼器自身會消耗地震產生的能量,這對于結構抗震是有利的。而且內置液體,本身沒有可計算的剛度,不影響整個結構的固有周期[6]。呈橢圓形的滯回曲線,保證了安置在結構上的阻尼器在最大位移的狀態下受力為零,最大受力情況下位移為零,這一性能對減小結構反應十分有利[7]。
3.2 阻尼器設置位置
地震中,梁與墩之間的位移越大,墩梁之間的相對速度才可能越大,而由式(1)可知,墩梁之間的相對速度越大,阻尼器輸出的阻尼力也就越大,阻尼器對結構的地震反應抑制作用也越大。因此,阻尼器應該安置在結構最大相對位移處。對于本橋,連續梁墩墩頂的相對位移均較大,而1、6號墩為邊墩,墩身及基礎均較小,2、5號墩為次主墩,墩身及基礎與剛構主墩相差不大。設置阻尼器后,橋墩受力會增大,考慮到橋墩及基礎的設置,決定只在次主墩每個墩頂設置4個阻尼器。
3.3 粘滯阻尼器參數的對比分析
最大阻尼力和最大沖程是確定阻尼器的主要指標,而阻尼系數和速度指數是阻尼器控制作用大小的2個關鍵參數[8]。目前對于非線性粘滯阻尼器的設計,最終目的是確定粘滯阻尼器的阻尼系數及速度指數。通過改變阻尼系數及速度指數,可以改善并提高控制效果,但同時也可能會增加阻尼器的最大輸出阻尼力,而最大阻尼力越大,阻尼器越昂貴[9]。因此,對于阻尼器的設計,實際上是一個結構設計、阻尼器參數設計、經濟效益綜合分析及減振預期控制目標的綜合設計過程。
粘滯阻尼器參數選取的不同,其對結構響應的影響也不同。因此,需對結構引入粘滯阻尼器的情況進行結構響應分析。式(1)中,V是與結構自身有關的參數,阻尼器參數的選取,主要考慮對阻尼器參數C、α進行參數敏感性分析,研究這些參數變化對結構響應的變化規律,為粘滯阻尼器設計參數的確定提供依據[10]。表1給出了金水溝特大橋阻尼器參數敏感性分析工況。
利用阻尼器減震,主要是控制結構的最大位移和結構關鍵點的內力水平,橋墩的配筋及基礎的承載力與墩底彎矩的大小密切相關,另外阻尼器輸出的最大阻尼力是影響減震措施造價的關鍵參數,一般來說,最大阻尼力越大,阻尼器越昂貴。綜上所述,圖4~圖9僅給出了不同阻尼器參數下,梁端墩梁相對位移、主墩墩底彎矩及阻尼器最大阻尼力的變化情況。地震時程中,結構的上述參數都是隨時間變化的,下圖僅給出了各參數地震反應中的最大值。
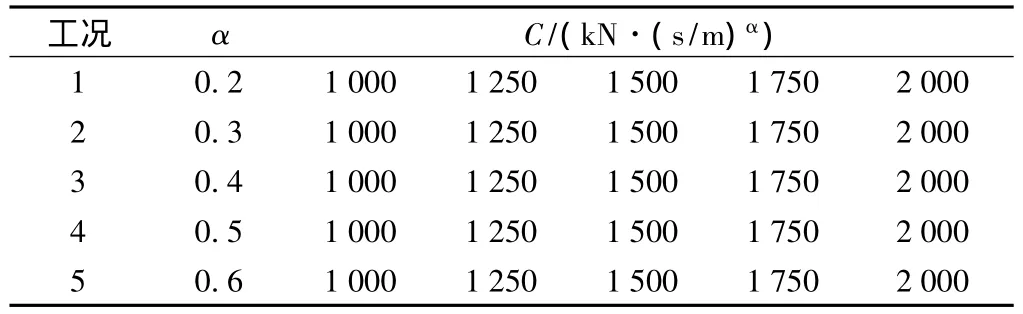
表1 金水溝特大橋阻尼器參數分析工況
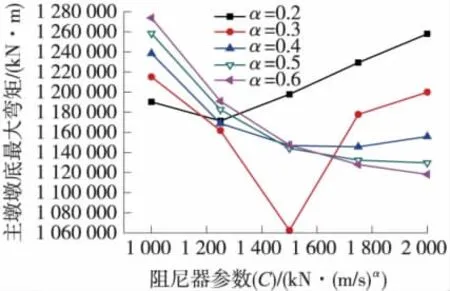
圖4 阻尼器參數C對主墩墩底最大彎矩的影響

圖5 阻尼器參數C對梁端最大相對位移的影響
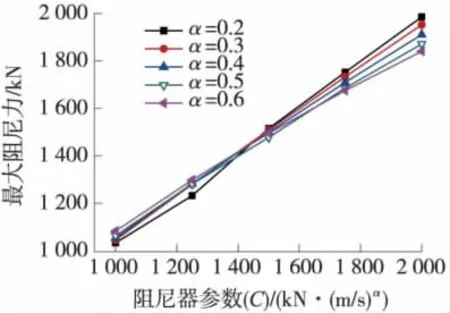
圖6 阻尼器參數C對阻尼器最大阻尼力的影響
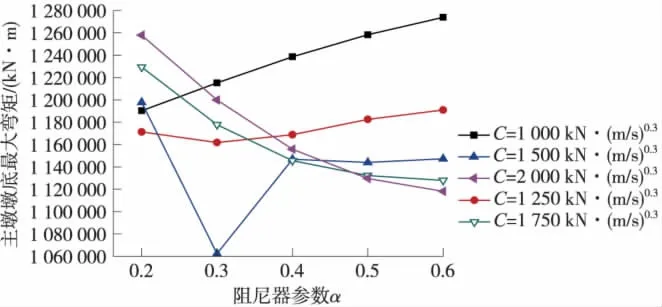
圖7 阻尼器參數α對主墩墩底最大彎矩的影響
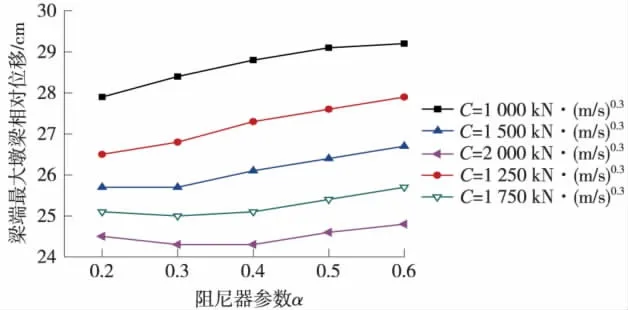
圖8 阻尼器參數α對梁端最大相對位移的影響

圖9 阻尼器參數α對阻尼器最大阻尼力的影響
由圖4可知,隨著阻尼器參數C的增大,墩底最大彎矩呈先單調遞減、后單調遞增趨勢,即參數C有最優化值。相同的C值下,α值不同,墩底最大彎矩也不盡相同,即對于墩底彎矩來說,C與α具有相關性。由曲線圖可知,當C值為1 500 kN·(s/m)0.3、α值為0.3時,墩底最大彎矩有極小值,此時的C與α值即為墩底彎矩的最優化參數。由圖5與圖6可知,阻尼器參數C越大,梁端最大相對位移越小,即對結構地震下的反應抑制效果越好,但是阻尼器的最大阻尼力也越大,所需阻尼器也就越昂貴。
由圖7可知,隨著阻尼器參數α的增大,墩底最大彎矩呈先單調遞減、后單調遞增趨勢,即參數α也有最優化值。由曲線圖可知,當 C值為1 500 kN·(s/m)0.3、α值為0.3時,墩底最大彎矩有極小值,此時的C與α值即為墩底彎矩的最優化參數。圖7與圖8的曲線接近于直線,即阻尼器參數α對梁端最大相對位移與阻尼器的噸位影響較小。但是不同C值下,曲線呈階梯狀,說明C值對梁端最大相對位移與阻尼器的最大阻尼力影響顯著。
3.4 粘滯阻尼器參數的確定
由粘滯阻尼器參數的對比分析可知,C值越大,梁端最大墩梁相對位移越小,但是阻尼器的最大阻尼力也越大。從圖8可以看出,C值從1 000 kN·(s/m)0.3變化到2 000 kN·(s/m)0.3,梁端最大相對位移僅減小了5 cm左右,但是阻尼器的最大輸出阻尼力卻增大了1倍。梁端最大墩梁相對位移及阻尼器最大阻尼力對參數α的變化不敏感,即α的取值對二者影響不大。對于主墩墩底彎矩來說,C與α有最優化值,當C取1 500 kN·(s/m)0.3、α取0.3時,主墩墩底最大彎矩有極小值,此時梁端最大墩梁相對位移為25.5 cm左右,阻尼器最大阻尼力為1 500 kN左右,阻尼器已經能很好的抑制結構縱向位移,并且阻尼器的最大阻尼力也不大。因此,綜合考慮阻尼器的減震效果及經濟效益,將 C為1 500 kN·(s/m)0.3、α取為0.3作為阻尼器最終的參數。
4 粘滯阻尼器的減震效果分析
將上述C與α值代入,取3條地震波,分析結構的地震反應,取各參數的最大值作為阻尼器減震下結構的最大反應。圖10與圖11給出了設置阻尼器前后梁端相對位移與主墩墩底彎矩的時程曲線,表2給出了設置阻尼器前后結構的地震反應計算結果。

圖10 設置阻尼器前后梁端相對位移時程曲線
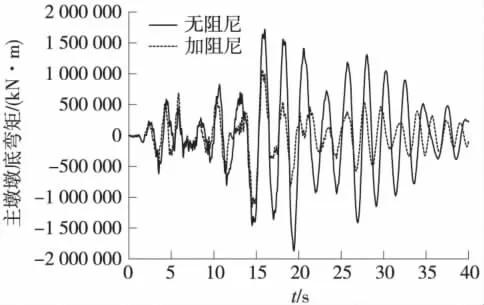
圖11 設置阻尼器前后主墩墩底彎矩時程曲線

表2 設置阻尼器前后結構的地震反應計算結果
圖10及圖11形象地反映了設置阻尼器后,梁端相對位移與主墩墩底彎矩顯著減小,阻尼器對結構的地震反應有較好的抑制作用。由表2可知,2號與5號次主墩墩頂設置阻尼器后,次主墩水平力雖然為原來的2倍多,但是由于阻尼器耗能的功勞,墩底彎矩反而較未設置時減少了將近30%。主墩的減震效果較為明顯,墩頂水平力減少了35%左右,墩底彎矩減少了38%左右。將主力與加阻尼器后的地震力組合并進行驗算,發現主墩基礎的承載力及橋墩樁基的配筋均能滿足要求。設置阻尼器后,次主墩墩頂的墩梁最大相對位移減小量超過50%,梁端的相對位移減為原來的65%左右,最大單邊位移不到13 cm,可以對梁端伸縮縫及邊墩頂帽起很好的保護作用。
由圖12知,阻尼器兩端最大的變形為±100 mm左右,而極限溫度+制動力+縱向風組合下結構最大靜位移為±75 mm,考慮到一定的安全值,可將阻尼器的沖程定為±200 mm。C取1 500 kN·(s/m)0.3、α取0.3時,阻尼器的最大輸出阻尼力為1 510 kN,兼顧安全并結合阻尼器的實際生產情況,所采用的阻尼器的最大阻尼力取1 600 kN。
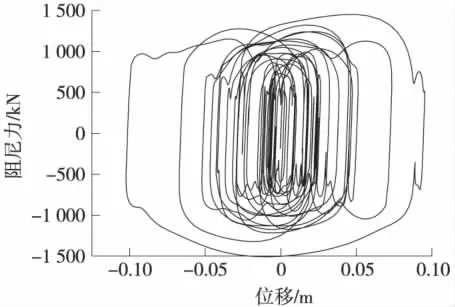
圖12 阻尼器的力-位移曲線
5 結論
通過對金水溝特大橋設置阻尼器前后地震下的反應進行分析,得到如下結論。
(1)對于鐵路高墩大跨剛構連續梁結構,地震力作用下,由于縱橋向承擔上部結構地震力的橋墩較橫橋向少,一般來說縱橋向的地震力更為控制設計。
(2)阻尼器參數的選取,應結合結構設計、減震效果及經濟效益綜合考慮。
(3)設置阻尼器后,全橋縱向的地震反應得到了很好的抑制,其中梁端的墩梁相對位移減少了35%左右,主墩墩底彎矩減少了38%左右,可以對梁端伸縮縫及邊墩頂帽起很好的保護作用,主墩基礎的承載力及橋墩樁基的配筋均能滿足要求,確保了地震下結構的安全。
(4)阻尼器最終的參數選取及設置情況為:在每個次主墩墩頂設置4個最大阻尼力為1 600 kN的液體粘滯阻尼器,阻尼器的沖程為 ±200 mm,C值為1 500 kN·(s/m)0.3,α 值為0.3。
(5)高墩大跨剛構連續梁結構,由于橋墩較柔,地震下連續梁墩墩頂的墩梁縱橋向相對位移較大,適合采用液體粘滯阻尼器來進行減震。
[1]中華人民共和國鐵道部.GB50111—2006 鐵路工程抗震設計規范[S].北京:中國計劃出版社,2009.
[2]中華人民共和國交通運輸部.JTG/T B02—01—2008 公路橋梁抗震設計細則[S].北京:人民交通出版社,2008.
[3]劉振宇,等.南寧大橋粘滯阻尼器參數分析[J].橋梁建設,2007(4):26.
[4]王志強,胡世德,范立礎.東海大橋粘滯阻尼器參數研究[J].中國公路學報,2005,18(3):38.
[5]斌 暄,王 磊,王歧峰.使用非線性粘滯阻尼器的橋梁在地震反應中的響應分析[J].公路交通科技,2007,24(10):77.
[6]魏錦濤.液體粘滯阻尼器及其在土木工程中的應用[J].四川建筑科學研究.2006,32(2):125.
[7]蔣建軍,周紅波.非線性粘滯阻尼器對懸索橋地震反應的影響[J].城市道橋與防洪.2004(6):100.
[8]陳永祁,耿瑞琦,馬良喆.橋梁用液體黏滯阻尼器的減振設計和類型選擇[J].土木工程學報,2007,40(7):57.
[9]蔣建軍,蔣勁松.廣西南寧大橋液體粘滯阻尼器設計[J].世界橋梁,2007(4):10.
[10]方 志.粘滯阻尼器參數對大跨度橋梁抗震性能影響研究[J].公路交通科技.2009,26(2):75.

