串行干擾抵消的靜態無線網絡上下文感知調度算法

呂紹和，王曉東，周興銘

（國防科技大學 計算機學院，湖南 長沙 410073）

1 引言

串行干擾抵消(SIC, successive interference cancellation)[1]是一種有效對抗干擾的多分組接收(MPR, multiple packet reception) 技術。多分組接收技術是物理層的重要進步，它試圖從沖突信號中解碼多個報文，從而消解沖突。然而，沖突信號只有在滿足一定條件時才可被解碼。因此，為確保MPR方法的可行性，需要細致協調網絡中各鏈路的傳輸。這就需要圍繞支持與利用 MPR而開展媒體接入控制層(MAC)與網絡層等上層協議的設計與研究。

具有SIC功能的接收節點使用迭代方式檢測多路傳輸信號。在每一次迭代檢測中，最強的信號被解碼，而其他信號被視為干擾。如果信號干擾噪聲比(SINR, signal to interference and noise ratio)不低于給定閾值，則該信號被解碼然后從混合信號中移除。在隨后的迭代檢測中，下一個最強的信號被解碼。這個迭代過程持續到所有的信號均被解碼或者迭代失敗。這種逐一解碼沖突信號的過程反映了SIC的順序檢測(sequential detection) 特性。

處理干擾是無線通信系統設計的主要難題之一。考慮在鏈路L2的接收節點處，鏈路 L1對鏈路L2的影響。一方面，若 L1的信號強度雖弱于 L2，但兩者并發時，L2的信號SINR不能達到閾值，則L2的接收將因 L1的干擾而失敗。另一方面，若 L1的信號強度足夠強于L2，則SIC可首先解碼并移除L1的信號從而消除它對L2的干擾。但此時，第三方的信號可通過阻止L1信號的解碼來達到干擾L2的效果。此外，干擾的累積效應(accumulative effect)也使得一個鏈路的干擾效果不單由其自身決定，還與其他并發鏈路緊密相關。累積效應是指當多份干擾信號并存時，總干擾為它們的累加。因此，在調度一條鏈路時，需要綜合所有先前已調度鏈路的影響，才能準確地刻畫當前鏈路的干擾效果。定義這些并發鏈路為當前鏈路的上下文(context)。基于累積干擾模型，本文研究了上下文感知的調度算法。

由于鏈路調度多為NP-hard問題，貪婪算法[2,3]作為一種有效的近似算法得到廣泛應用。通常，貪婪鏈路調度算法主要包括2個階段：鏈路選擇與時間槽選擇。前者選擇下一個將被調度的鏈路，而后者則為當前鏈路分配合適的時間槽。現有調度算法著重于鏈路選擇策略的研究，而在時間槽選擇階段采用簡單的首次匹配(first fit)策略。首次匹配是指對給定的鏈路L，從第一個時間槽開始，按序尋找可分配給L的xL個時間槽(xL為L所需時間槽的數目，xL≥1)。在鏈路選擇階段，這些算法通過利用干擾信息來設計合理的選擇策略。然而，衡量鏈路的干擾狀況，需要知道它的上下文信息，這些信息在為鏈路分配時間槽之前無法獲知。因此，現有調度算法對鏈路干擾信息的獲取與利用都極不充分，這嚴重限制了它們的性能。

相關工作：無線網絡的干擾模型主要包括累積干擾模型[2]與非累積干擾模型[3]。已經證明，在 2類模型下，無線網絡中的鏈路調度都是NP-hard問題[3]。因此，貪婪算法廣泛用于構造近似最優的調度，例如基于非累積干擾模型的調度[3]與基于累積干擾模型的調度[2]。當網絡節點具備多分組接收能力時，需要新的干擾模型以反映此時的干擾特征。在Celik等的工作中[4]，累積干擾模型得到了擴展。此時，SINR閾值被設置為小于1的某個值，從而使得沖突信號中的多個報文可被解碼。該模型的缺陷在于它沒有考慮沖突中不同信號的差別，因而無法刻畫SIC的順序檢測特征。

Lv等[5]以非累積干擾模型為基礎，給出了一個刻畫SIC特征的干擾模型。它準確捕捉了當接收節點具有SIC能力時，并發的多條鏈路之間所存在的依賴性(correlation)。它的不足在于，未考慮無線干擾的累積效應。此外，Gelal等[6]研究了支持SIC的多用戶 MIMO無線網絡中的拓撲控制。最近，Lv等[7]提出沖突集圖(conflict set graph)以建模支持SIC時無線網絡中的干擾。但在最壞情況時，該方法的時間復雜度是指數級的。

主要貢獻：提出了一種新的貪婪算法，即上下文感知調度算法。首先，給出加權并發圖以描述支持SIC時無線網絡的干擾。然后，著重研究了時間槽選擇階段的設計，即對于給定鏈路，若存在多個可用時間槽，是否首次匹配的時間槽一定為最佳，或如何選擇最佳的時間槽？基于鏈路的上下文信息，定義容忍度以衡量鏈路集的飽和度(即接納新的鏈路的能力)并給出2種啟發式的策略：①選擇時間槽使得該時間槽鏈路集的容忍度最大；②選擇時間槽使得該時間槽鏈路集的容忍度變化最小。仿真結果表明，所提方案的性能優于首次匹配策略。

本文的剩余部分組織如下。第2節描述系統模型，第3節與第4節分別給出加權并發圖與上下文感知貪婪調度算法，第5節給出仿真實驗結果，第6節總結全文。

2 系統模型

考慮一個含N個靜態節點與n條鏈路的單信道無線網絡。鏈路標記為 Li，其傳輸節點為 Si且接收節點為 Ri，其中， i = 1 ,2,… ,n 。假定：①SIC中信號的移除是無誤差的；②每一個節點配有一個全向天線，工作于半雙工模式且在同一時刻不能發送多個報文。

SIC的順序檢測：考慮2條鏈路 L1與 L2。當在R1處，來自 L2的信號功率足夠強，使得在有 L1的信號干擾下， L2的信號仍能被 R1檢測。然后，通過移除 L2的信號， R1可完成對 L1信號的解碼。此時，

稱1L依賴于2L且2L為1L的相關鏈路。所滿足條件是

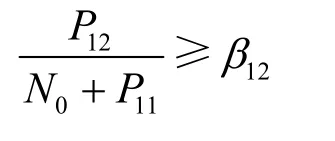
其中，Pij是節點 Ri處，來自節點 Sj的信號的接收能量；N0為噪聲強度；βij為節點Ri解碼來自節點Sj的信號所需的最低SINR。

常用的無線干擾模型包括非累積模型與累積模型2類。前者僅考慮鏈路兩兩之間的關系，后者則考慮了干擾的累積效應。累積干擾模型更真實反映了無線干擾的特點。為刻畫SIC的特征，下面給出一種模型。它對沖突中的所有鏈路，依據它們的信號強弱而排序，因此被稱為有序累積干擾模型(order-aware physical interference model)。

有序累積干擾模型：考慮 Ld的接收。設共有J( J ≤n-1)條與Ld并發的鏈路，其中D (D≤J)條是 Ld的相關鏈路。不失一般性，所有鏈路按照在Rd的接收功率排序為 Li1,Li2,… ,LiJ+1。假設ik= d ，則Piki1≥ Piki2≥ … ≥ PikiJ+1，相關 鏈路的集 合為{Li1,Li2,… ,LiD}。為成功檢測Ld的信號，要求

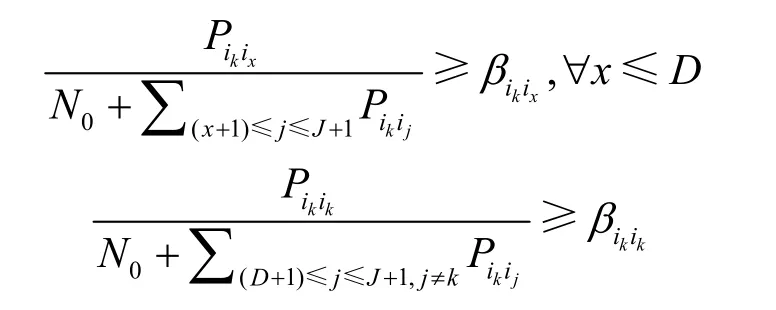
當一組鏈路并發時，通過有序累積干擾模型，每條鏈路的傳輸成敗均可準確判斷。當鏈路集 LS并發時，若對任意鏈路 L∈LS，L的傳輸均成功，則稱LS為可行鏈路集(feasible link set)，簡稱為可行集。鏈路調度可轉化為尋找多個可行集的問題(詳見第4節)。因此，下面討論如何建模網絡干擾及如何尋找可行集。

3 加權并發圖

圖是無線網絡十分常用的建模手段。Jain等[8]給出沖突圖(conflict graph)，它的每個頂點包含一條鏈路。當2條鏈路不可并發時，相應的2個頂點有邊相連。為反映干擾的累積效應，Brar等[2]給出加權沖突圖(weighted conflict graph)，它的任意2頂點均相連，且權重設為鏈路之間的干擾強度。這些工作未考慮SIC的順序檢測特性。

Lv等[5]指出，對鏈路1L與2L，若它們的并發需要SIC的支持，則它們之間存在一種依賴關系。為此，Lv等引入一類新的圖頂點——超頂點(SV,super vertex)，它同時包含鏈路及其所依賴的鏈路。與之相比，普通頂點(OV, ordinary vertex)則僅包含單條鏈路。據此，Lv等提出并發圖(SG，simultaneity graph)以描述支持SIC時的網絡干擾。但是，并發圖未考慮無線干擾的累積效應。

網絡干擾建模面臨的主要挑戰是處理SIC的順序檢測特性與干擾的累積效應。下面給出加權并發圖(WSG，weighted simultaneity graph)。它的主要思想是通過權重反映鏈路之間的干擾，而權重之和則反映干擾的累積效應。

3.1 構造

具體地，令SGW=(V, E, WV, WE)表示一個WSG，其中，V為頂點集，E為有向邊的集合，WV與WE分別為點權(vertex weight)與邊權(edge weight)的集合。

SGW包含2類不同的頂點。

普通頂點對應于單條鏈路。對鏈路 Li，建立OV (Li)。令 vi= Pii代表Li的權值。

對每條鏈路Li及其每條相關鏈路Lj，構造SV(LiLj)。SV中鏈路的先后順序十分重要。例如，若Li依賴于Lj且Lj依賴于Li，則需要建立2個超頂點(LiLj)與(LjLi)。令 vij= Pij代表超頂點(LiLj)的權值。

SGW中有2類不同的邊。

建立Lj到Li的邊，若 Pij＜ ( Pii+ N0)βij(即 Lj不是Li的相關鏈路)。令 eij= Pij表示該邊的邊權。

建立 Lj到(LiLk)的邊，若 ( Pii+N0)βij≤Pij≤Pik(即Lj與Lk均為Li的相關鏈路，且在Ri處Lk的信號強于Lj的信號)。令 eijk= Pij表示該邊的邊權。

與加權沖突圖不同，SGW中的頂點不需要兩兩相連。當Lj是 Li的相關鏈路時，無需建立Lj到Li的邊。這是因為在節點Ri，Lj的信號先于Li的信號被解碼。在解碼Li的信號時，Lj的信號已被移除，不產生任何干擾。類似地，當Lj與Lk均為Li的相關鏈路，且在Ri處Lk的信號強于Lj的信號，無需建立Lk到LiLj的邊。

圖1給出了加權并發圖的一個例子，圖1(a)為包含4條鏈路L1,…,L4的網絡，其中，L2與L3為L1的相關鏈路，且 S2、S3、S1與 S4到 R1的距離依次遞增。以鏈路L1為例說明SGW的構造過程。首先，對 4條鏈路，建立 4個普通頂點(L1～L4)；由于 L2與L3為L1的相關鏈路，建立超頂點L1L2與L1L3。其次，由于鏈路L4并非L1的相關鏈路，建立L4到L1的邊，且邊權為 P14；由于L2與 L3為 L1的相關鏈路，無需建立L2與L3到L1的邊。由于P13＜P12，建立 L3到 L1L2的邊，且邊權為 P13；無需建立 L2到L1L3的邊。最后得到的加權并發圖如圖1(b)所示(為清晰起見，各頂點的權值未給出)。

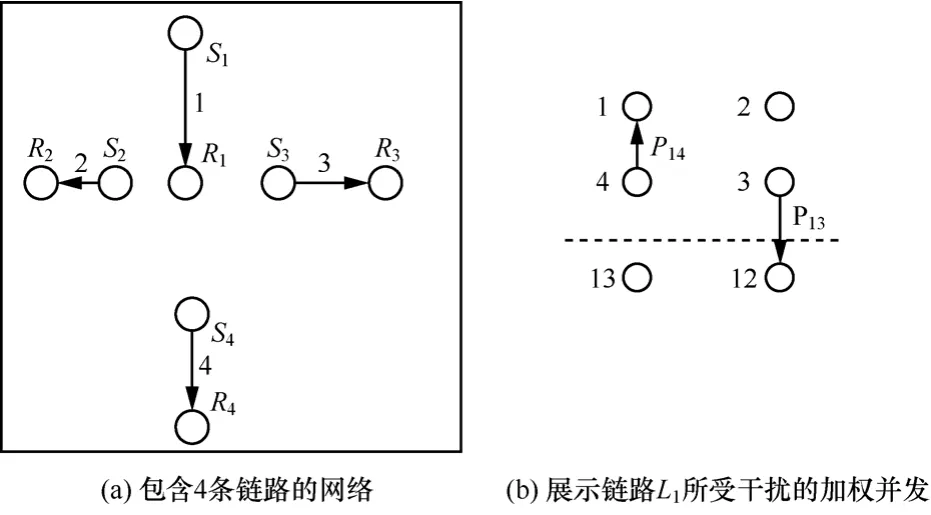
圖1 加權并發圖的實例

3.2 討論

在給出調度算法之前，先簡要討論2個重要的問題：①加權并發圖的構造方法；②SIC的實現復雜度等的考慮。

加權并發圖的構造，關鍵在于接收能量Pij的獲取。對此，Qiu等[9]與Reis等[10]給出了一種基于測量的方法，它的基本思想是：當沒有鏈路傳輸時，接收節點可測量到噪聲強度N0；對鏈路Lj，在某個時間槽上，僅允許Sj發送報文，此時對任意接收節點Ri，它所測量到的接收能量就是(N0+Pij)；對每條鏈路，均執行該過程，就可得到所有的 Pij(1≤i,j≤n)。顯然，該方法對靜態無線網絡有效，一旦網絡拓撲出現動態變化，就需重新執行以上的測量過程。當網絡具有較強的動態性時，該方法的開銷與時效性都變得很不理想。對動態的無線網絡，如何及時地獲取它的狀態信息，本身仍是一個極具挑戰性的問題。就鏈路調度而言，當網絡經常動態變化時，現有的調度策略可能并不適用。此時，需要某種機制對網絡的動態性予以跟蹤、分析與預測。這超出了本文的研究范圍。

SIC的思想十分簡單，但它的計算量、控制邏輯等實現上的復雜度不可輕視。硬件設計工藝及軟件無線電(SDR, software-defined radio)等新技術的進步，有助于克服這方面的難題。最近，Halperin等[11]在SDR平臺實現了SIC并通過實驗分析了SIC對網絡性能的影響。作為一種復雜的信號處理算法，SIC的實現最關鍵的地方是對性能與代價的取舍。Weber等[12]指出，僅需不超過2次的迭代解碼，SIC就能大幅度提高網絡性能；同時，繼續增大迭代解碼的次數，并不能顯著改善網絡性能。因此，SIC的實現可大大簡化。通過避免復雜的高階迭代，便能以少量的性能損失，換取實現難度的降低。

4 上下文感知的調度

由于干擾的累積效應與SIC的順序檢測特性，除非鏈路的上下文已完全指定，否則難以精確評估鏈路干擾。這使得在鏈路選擇階段，可利用的干擾信息極為有限。為此，研究時間槽選擇階段干擾信息的利用并據此提出新的調度算法。

4.1 貪婪算法的一般過程

以TDMA(time division multiple access)為背景，研究鏈路調度(link scheduling)問題。TDMA將時間劃分為等長的時間槽(time slot)，每個時間槽可用以完成一個報文的傳輸。假設每條鏈路僅需要一個時間槽，鏈路調度問題是：給定加權并發圖，尋找一組鏈路集滿足：①每條鏈路均含于某一個鏈路集；②每個鏈路集均為可行集；③鏈路集的數目為最小。

定理1 在支持SIC的無線網絡中，基于累積干擾模型的鏈路調度問題為NP-hard。

證明 對于任意鏈路iL以及每一個ji≠，令閾值ijβ→∞。那么，iL除了需要的信號，不能解碼其他任何信號。該問題自然退化成無SIC的鏈路調度問題，這已在文獻[8]中證實為NP-hard問題。因此，作為更普遍的情況，本文的問題也是NP-hard。

證畢。

由于尚不存在NP-hard問題的多項式時間最優解法，貪婪算法作為有效的近似方案得到廣泛的研究。貪婪調度主要包含鏈路選擇與時間槽選擇等 2個階段。圖2給出了貪婪調度的一般過程：①鏈路選擇，在未調度鏈路的集合中依據給定的指標選擇一條鏈路，令Li表示該鏈路；②時間槽選擇，在已分配時間槽中尋找對Li可用的時間槽。一個時間槽對 Li可用是指將 Li調度到該時間槽后，包括 Li的所有已調度鏈路均能成功傳輸，若不存在可用時間槽，則分配新的時間槽，若有多個可用時間槽，算法將為Li選擇最佳的時間槽。以上過程不斷重復至所有鏈路均被調度。

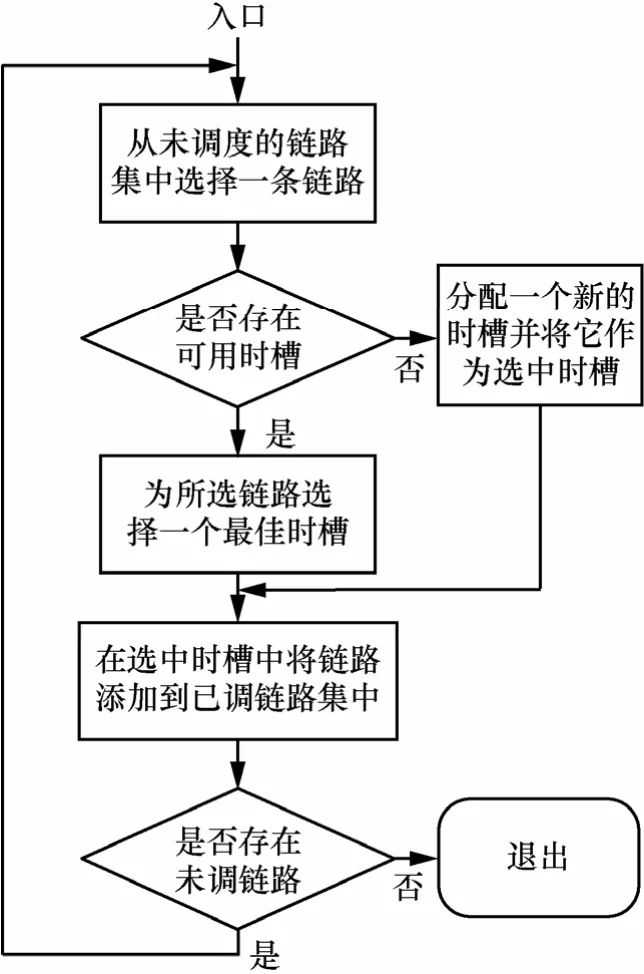
圖2 貪婪調度算法的流程

現有調度[2,3,7]在時間槽選擇階段多采用首次匹配策略，即總選擇第一個可用時間槽。它們試圖在鏈路選擇階段利用干擾信息以獲得良好性能。這種設計的合理性來源于對圖著色(graph coloring)問題的研究。圖著色是圖論的經典問題，它的研究結果指出，通過合理排序頂點，基于首次匹配的貪婪算法可得到最優或近似最優的解[7]。然而，圖模型只考慮了鏈路兩兩之間的干擾，這在非累積干擾模型下是可行的。但在累積干擾模型下，鏈路干擾的影響還與它的并發鏈路緊密相關。在鏈路選擇階段，這些并發鏈路即上下文，還無法確定，這嚴重限制了調度算法的性能。

據此，提出上下文感知的調度并著眼于時間槽選擇階段的設計。新方案的基本思想是，即使以任意方式排序鏈路，通過設計合適的時間槽選擇策略也能得到好的調度。此時，算法設計的主要任務是合理評估每個時間槽是否適合于調度當前鏈路。該評估的關鍵在于準確刻畫當前鏈路被調度后所產生的干擾。此時，每個時間槽上已調度的鏈路，提供了評估當前鏈路所需要的上下文信息。

4.2 鏈路集的飽和度

不妨記 Ski為在調度鏈路 Li前調度到時間槽 tk的鏈路集。則將Li調度到tk上所產生的干擾就體現為 Ski∪{Li}與 Ski在飽和度(即接納新鏈路的能力)上的差異。對鏈路集LS與鏈路L，若 L S∪{L}為不可行集時，稱鏈路集LS對于L飽和。顯然，空集合的飽和度最小。任何新鏈路的加入都可能增大鏈路集的飽和度。但若新鏈路的干擾可通過SIC消除，則它的加入并不會改變鏈路集的飽和度。鏈路集LS的飽和度通過LS中的鏈路的抗干擾能力體現。

定義1 鏈路L∈LS的容忍度(tolerance margin)是指當LS的所有鏈路并發時，鏈路L所能容忍的最大干擾。

給定加權并發圖，算法1給出了容忍度的計算過程。該容忍度是以下干擾值的較小者：①干擾L的任意一條相關鏈路的信號解碼所需的最小干擾；②在所有相關鏈路的信號均被移除后，干擾L的信號解碼所需的最小干擾。算法的 2)～3)行計算第②部分，而4)～10)行則計算了第①部分。鏈路的容忍度與可行性存在以下關系，其正確性不難證明。

定理2 鏈路集LS中的鏈路L可行，當且僅當L的容忍度大于0。

定理3 算法1的時間復雜度為O(|LS|2)，其中，|LS|為LS所含鏈路的數目。

證明 首先，第 2行需要遍歷頂點 Li與 Lx(Lx∈LS)之間的邊，其復雜度不超過O(|LS|)。其次，第 4)～10)行需要遍歷所有形如 LiLy(Ly∈LS)的超頂點及其與 Lx(Lx∈LS)的邊。每個超頂點的邊數不超過O(|LS|)，而超頂點的數目不超過O(|LS|)。因而，復雜度不超過 O(|LS|2)，即算法的時間復雜度為O(|LS|2)。 證畢。

算法1 容忍度的計算

輸入：SGW=(V,E,WV,WE)：加權并發圖

LS：鏈路集; Li：LS中的鏈路

輸出： Li的容忍度

以圖1中鏈路L1為例說明容忍度的計算。首先，移除相關鏈路的信號后，L1所受干擾為L4的信號與噪聲。從而L1還能承受的干擾為M1=P11/11β-N0-P14。其次，考慮R1對相關鏈路信號的解碼。對鏈路L2，鏈路L1與另一條相關鏈路L3的信號均為干擾，它的信號解碼還能承受的干擾為M2=P12/β12-N0-P14-P13-P11。類似地，對鏈路L3，它的信號解碼還能承受的干擾為M3=P13/β13-N0- P14-P11。最終，鏈路L1的容忍度為{M1, M2, M3}的最小值。

定義2 鏈路集LS的容忍度，記為 MLS，是指它在可行的前提下所能容忍的最大干擾。

集合的容忍度是其每條鏈路容忍度的最小值。鏈路集容忍度的計算方法如下：對鏈路集的每條鏈路應用算法 1，然后取所有結果中的最小值。對L?LS，若有 MLS∪{L}≥0，則稱LS對L可行。容忍度衡量了鏈路集的飽和度。空集合的容忍度為無窮大。新鏈路的加入，將可能導致容忍度的降低與飽和度的增加。最終，當容忍度降低到一個臨界點，任何未調度鏈路的加入都將使得鏈路集為不可行，就稱鏈路集達到飽和。類似地，對鏈路集的容忍度與可行性，存在如下關系。

定理4 鏈路集LS可行，當且僅當LS的容忍度大于0。

首次匹配策略的次優性在于其簡單選擇第一個可行的時間槽，而忽略了時間槽上所調度鏈路集的容忍度。考慮 2條鏈路 L1與 L2，假設P12/(N0+ P11) = β12。由于SIC可在L1的接收節點移除L2的信號，L1與L2可并發。但若它們并發，由于 M{L1,L2}= 0 ，任何其他鏈路都不能再調度到該時間槽上。從全網優化的角度看，將兩者分配到不同時間槽，或許能得到更好的結果。因此，任意方式選擇時間槽可能會增大最終所需的時間槽數目。

4.3 上下文感知調度

現在給出上下文感知的調度算法CONG，其過程如算法 2所示。首先將所有鏈路任意排序為l1, l2,… ,ln。在li調度之前，令Ni為已用時間槽的數目，Sij為在第j個時間槽上所調度的鏈路集。CONG按如下方式從l1開始依次處理每一條鏈路：①對每個計算的容忍度；②若Ni=0或對所有1 ≤ j≤ Ni，Sij對 li均不可行，則分配新時間槽以調度 li。否則，在所有可用時間槽中選擇一個以調度 li。在處理完所有鏈路后，CONG返回總時間槽數目與每個時間槽上所調度的鏈路集。顯然，所有鏈路集均為可行集。

算法2 上下文感知貪婪調度算法CONG

輸入：SGW=(V,E,WV,WE)：加權并發圖

輸出：時間槽的數目M及調度S1,…,SM

定理5 算法2的時間復雜度不超過O(n3)，其中n為網絡所含鏈路的數目。

證明 首先，對任意的鏈路集Sk，計算它的容忍度，時間開銷不超過 O(|Sk|2)。同時，注意到而所有 Sk的鏈路總數不超過 O(n)。因此，第 4)～6)行的總時間開銷不超過 O(n2)。其次，第 7)～10)行的時間開銷為常數，而第 11)行所需的容忍度信息已被計算，選擇過程的開銷為 O(M)≤O(n)。總之，一次循環(第 4)～11)行)所需時間為 O(n2)。循環執行的次數不超過O(n)。從而，總的時間開銷不超過 O(n3)。

證畢。

下面給出2種選擇時間槽的策略。

最大殘余優先（LRF, largest residue first）：在所有可用時間槽中，選擇具有最大容忍度的第一個時間槽。對鏈路 li，選擇第k個時間槽的條件：k是 TliΔ中的最小值，

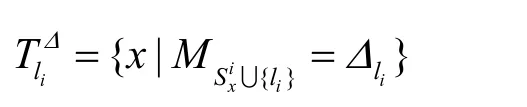
最小減量優先（MDF, minimum decrease first）：在所有可用時間槽中，選擇容忍度降低最小的第一個時間槽。對鏈路li，選擇第k個時間槽的條件：k是ilTδ中的最小值，

2種策略的共同目標是將更多的鏈路調度到已選的時間槽中。一般地，容忍度越大，鏈路集接收新鏈路的能力越強。LRF的選擇平衡了不同時間槽上的容忍度，避免在調度早期就導致大量時間槽上的鏈路集達到飽和。而MDF則更著眼于最小化當前鏈路被調度所產生的干擾。圖3給出的例子展示了LRF與MDF的區別，假設調度il之前已使用 3個時間槽。由于LRF選擇1t時間槽。然而，由于MDF選擇3t時間槽。下面通過仿真實驗考察 2種策略的性能。

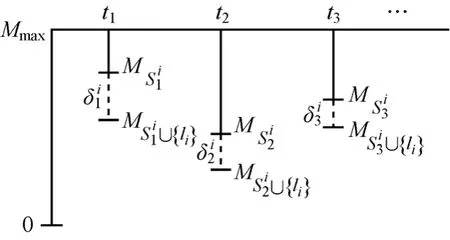
圖3 LRF與MDF區別的例子

5 性能評估

通過網絡仿真器(NS 2, network simulator 2)[13]的仿真實驗評價了近似方案的性能。表1總結了仿真過程中參數和協議的設置。評測性能指標為吞吐量，其中，平均吞吐量為總吞吐量(aggregate throughput)的平均，平均鏈路吞吐量為單條鏈路所獲得的吞吐量的平均值。每一個數據點都是通過對多次運行結果取平均值獲得。通過與首次匹配策略的比較來考察新調度機制的性能。2種新策略與首次匹配的實驗結果分別用 LRF、MDF與 First-Fit表示。

NS 2并未提供對基于SINR模型的報文接收與SIC功能的支持。首先增加新的模塊以支持累積干擾模型與SIC，詳細描述可參考文獻[5,7]。表1中的傳輸范圍是指無其他并發傳輸時鏈路能正常通信的最大距離。若無特別說明，在每個時間槽的開始，每個源節點都依概率η發出一個報文。該概率對所有源節點均相同。

表1 仿真參數

首先在單跳情況下評估調度算法的性能。在150m×150m的區域內，隨機分布100個節點并隨機選取其中25個節點作為源節點。圖4給出3種算法所得到的吞吐量。作為參考，利用數學規劃可得到此時的最大吞吐量，用Optimal表示。LRF與MDF的表現很好。相比于First fit策略，LRF與MDF在吞吐量上的優勢高達30%。此外，隨著傳輸概率的增大，First-fit的吞吐量急劇下降。這是因為實驗中鏈路以任意方式排序，當鏈路的數目很大時，每條鏈路的時間槽以First-fit方式任意選擇，導致最終的調度性能很不理想。LRF與MDF的性能基本相當。但是，也必須看到，3種近似算法與優化值均有一定距離，設計更好的時間槽選擇機制仍需進一步研究。

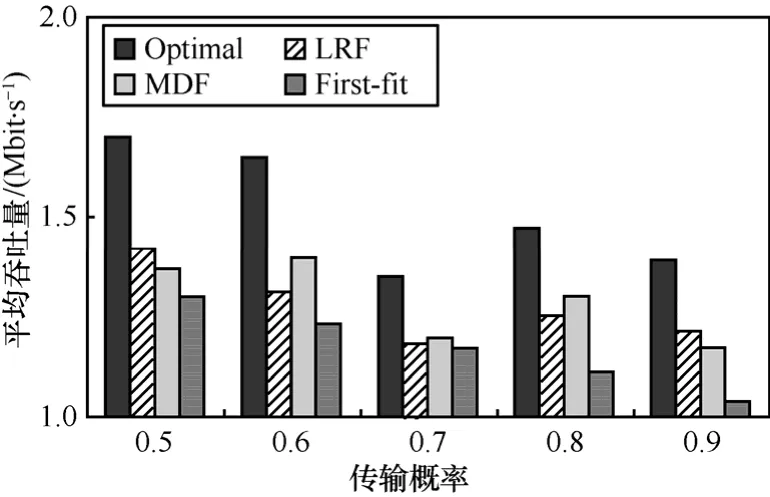
圖4 單跳網絡中平均吞吐量與傳輸概率的關系

為考察在較大規模的網絡中SIC的效果，在一個500m×500m的區域內，均勻部署81個節點并隨機選取其中30個節點作為源節點。對每個源節點，在其通信范圍內隨機選擇一個節點作為目標節點。圖5給出平均吞吐量與傳輸概率η之間的關系。考慮另一種流模式，令(x, y) (1≤x≤9, 1≤y≤9)表示不同位置的節點，考慮以下3種流模式：①P1:(x, 1)→(x, 9)；②X1: (x, 2)→((x+7) mod 9, 7)；③X2: (x, 9)→((x+7) mod 9, 1)。v1 mod v2 為取模運算，它返回v1除以v2的余數。每種流模式下均有9個不同的數據流。這些數據流可能需要多跳傳輸。不同流模式下，所需的轉發鏈路數也不同。其中，P1所需鏈路數最小，X1次之，而X2所需最多。圖6給出了3種流模式的吞吐量。

圖5對應的場景中，隨著η的增長，活躍鏈路的數目將逐漸增大。圖 6對應的場景中，從 P1、X1到X2，總鏈路數目亦不斷增多。隨著網絡包含越來越多的鏈路，可以預期在網絡中將存在更多并發傳輸的機會。這些場景中，LRF與MDF展示出了明顯優于First-fit的性能。

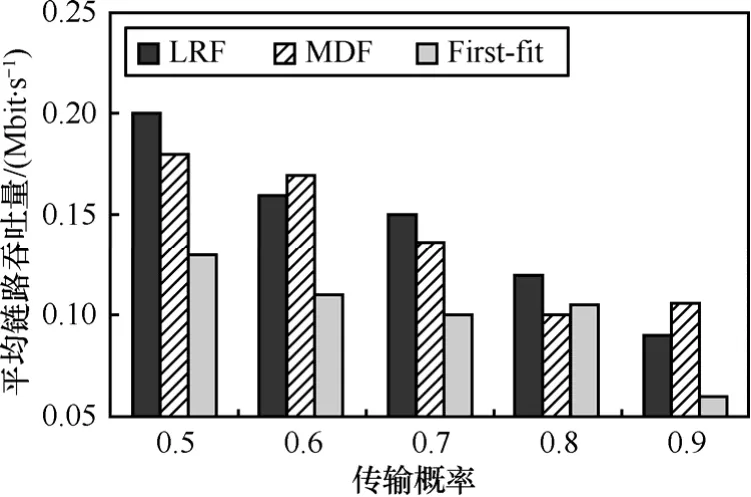
圖5 81節點均勻分布的網絡中平均鏈路吞吐量與傳輸概率的關系

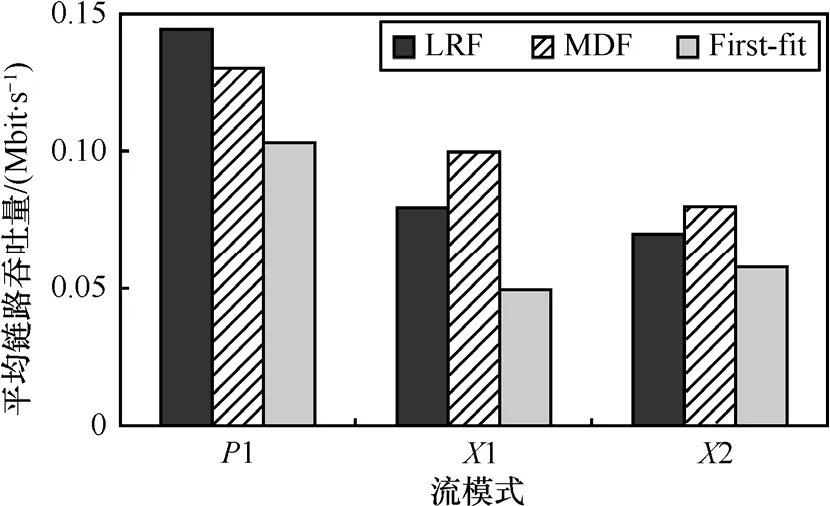
圖6 81節點均勻分布的網絡中不同流模式時的平均鏈路吞吐量

最后，在一個 500m×500m的區域內隨機方式部署100個節點。然后隨機選取其中的30個節點作為源節點。對每個源節點，以隨機方式選擇目標節點。此時，一些節點對的傳輸需要多跳路由，所有活躍鏈路的總數在 30～48之間。圖 7給出了在η= 0 .8時，平均吞吐量與鏈路數目的關系。與First-fit相比，LRF與MDF的吞吐量增益可達27%。

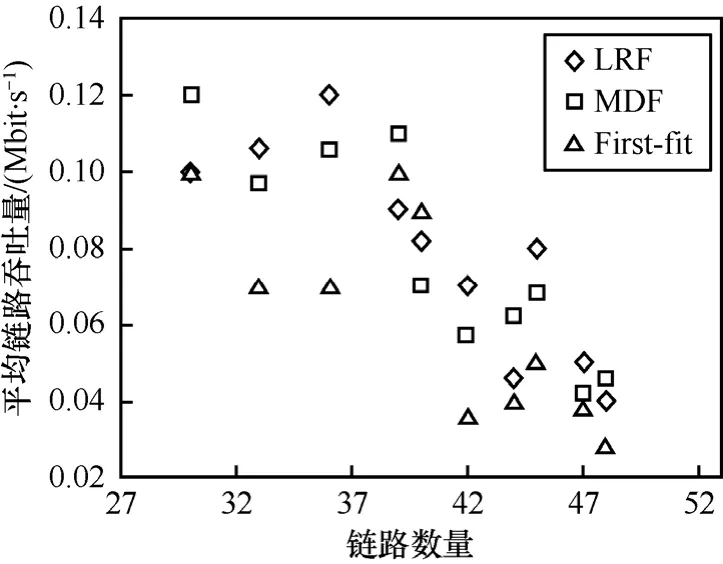
圖7 100個節點隨機分布的網絡中平均鏈路吞吐量與鏈路數目的關系

6 結束語

本文研究了支持 SIC的靜態無線網絡中基于累積干擾模型的鏈路調度。首先給出加權并發圖以描述網絡干擾，并指出鏈路調度為NP-hard問題。然后，重點研究了貪婪調度算法。由于SIC的順序檢測特性與干擾的累積效應，如何準確衡量鏈路干擾是主要的研究挑戰。現有的貪婪調度方法不能充分地理解與利用干擾信息，導致它們的性能不夠理想。本文定義了容忍度以衡量鏈路集的飽和度，然后給出2個高效的策略為給定的鏈路選擇最佳時間槽。在仿真實驗中，2種策略的性能均優于常用的首次匹配策略。

[1] ANDREWS J. Interference cancellation for cellular systems: a contemporary overview[J]. IEEE Wireless Communications, 2005, 12(2): 19-29.

[2] BRAR G, BLOUGH D, SANTI P. Computationally efficient scheduling with the physical interference model for throughput improvement in wireless mesh networks[A]. ACM MOBICOM’06[C]. Los Angeles,USA, 2006. 2-13.

[3] WANG W, LI X, FRIEDER O, et al. Efficient interference-aware TDMA link scheduling for static wireless networks[A]. ACM MOBICOM’06[C]. Los Angeles, USA, 2006. 262-273.

[4] CELIK G, ZUSSMAN G, KHAN W, et al. MAC for networks with multipacket reception capability and spatially distributed nodes[A].IEEE INFOCOM’08[C]. Phoenix, USA, 2008. 1436-1444.

[5] LV S, ZHUANG W, WANG X, et al. Scheduling in wireless ad hoc networks with successive interference cancellation[A]. IEEE INFOCOM’11[C]. Shanghai, China, 2011. 1282-1290.

[6] GELAL E, PELECHRINIS K, KIM T, et al. Topology control for effective interference cancellation in multi-user MIMO networks[A].IEEE INFOCOM’10[C]. San Diego, USA, 2010. 2357-2365.

[7] LV S, WANG X, ZHOU X. Scheduling under SINR model in ad hoc networks with successive interference cancellation[A]. IEEE GLOBECOM’10[C]. Miami, USA, 2010. 1-5.

[8] JIAN K, PADHYE J, PADMANABHAN V, et al. Impact of interference on multi-hop wireless network performance[A]. ACM MOBICOM’03[C]. San Diego, USA, 2003. 66-80.

[9] QIU L, ZHANG Y, WANG F, et al. A general model of wireless interference[A]. ACM MOBICOM’07[C]. Montreal, Canada, 2007. 171-182.

[10] REIS C, MAHAJAN R, RODRIG M, et al. Measurement-based models of delivery and interference in static wireless networks[A]. ACM SIGCOMM’06[C]. Pisa, Italy, 2006. 51-62.

[11] HALPERIN D, ANDERSON T, WETHRALL D. Taking the sting out of carrier sense: interference cancellation for wireless LANs[A]. ACMMOBICOM’08[C]. San Francisco, USA, 2008. 339-350.

[12] WEBER S, ANDREWS J, YANG X, et al. Transmission capacity of wireless ad hoc networks with successive interference cancellation[J].IEEE Trans Information Theory, 2007, 53(8): 2799-2814.

[13] NS-2, Network simulator version 2[EB/OL]. http://www.isi.edu/nsnam/ns/ [EB/OL]. 2010.