考慮剪切變形及轉動慣量的H型鋼梁自由振動*

李靜斌，陳 淮，葛素娟

(鄭州大學土木工程學院，河南 鄭州 450001)

H型鋼是一種典型的熱軋型鋼，在各種鋼結構體系中均有廣泛的應用。其中，最常見的結構應用是作為土木工程中的簡支單梁。在進行結構動力分析或動力設計時，需要準確把握其動力特性，特別要求對自由振動頻率進行精確求解。工程實踐中，對H型鋼梁進行自由振動分析，往往采用不考慮剪切變形及轉動慣量影響的初等梁理論模型。對于長細比較大的梁，頻率的計算誤差可能還不明顯;但隨著梁長細比的減小，初等梁理論模型的計算誤差將會越來越顯著，從而不能滿足工程設計必要的精度的需要［1－7］。本文通過對3種典型熱軋H型鋼截面簡支梁自由振動頻率的計算，對比初等梁理論和考慮剪切變形及轉動慣量影響的高等梁理論的差異，以便為工程結構分析及動力設計提供一種簡單易用的理論選用標準。

1 梁自由振動控制微分方程

考慮無阻尼直梁，設梁的彎曲剛度為EI(x)，單位長度的質量為m(x)，梁垂直于軸線方向的橫向位移用v(x，t)表示，隨時間和位置變化的外力用p(x，t)表示。根據D’Alembert原理，引入橫向剪力V(x，t)及橫向彎矩M(x，t)，由力平衡條件可以得出［8－9］:

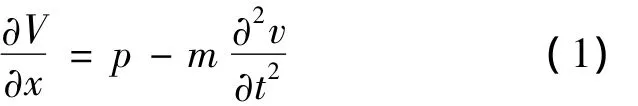
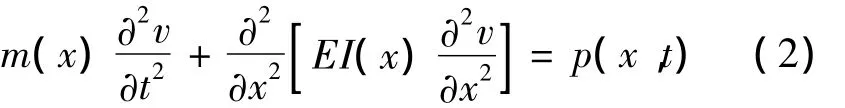
對于自由振動的情況，方程(2)的右端為0。考慮等截面直梁，即EI(x)=EI，m(x)=m，則等截面直梁自由振動微分方程可簡化為:

對方程(3)的求解可采用分離變量法，引入參數β4=ω2m/EI后，可將梁自由振動的振型函數設為 φ(x)= C1sinβx+C2cosβx+C3sinhβx+C4coshβx，代入梁端邊界條件，可求出4個待定常數 C1，C2，C3和 C4。

以簡支梁為例，代入x=0及x=L處的邊界條件 v(0，t)=0和 M(0，t)=0，可得C2=C3=C4=0，并可導出頻率方程C1sinβL=0，因C1≠0，故可解得初等梁理論等截面簡支直梁的自由振動頻率:

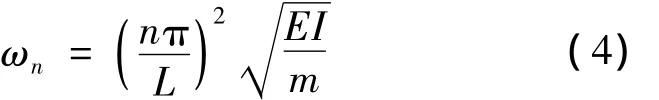
2 考慮剪切變形及轉動慣量的梁自由振動

在方程(2)或(3)的推導過程中，忽略了與梁截面轉動有關的慣性矩，并忽略了梁中因剪切變形引起的撓曲。若考慮剪切變形及轉動慣量的影響，則等截面直梁自由振動微分方程為:

仍考慮1個兩端簡支的等截面直梁，假定其解的形式為v(x，t)=Csin(nπx/L)sinω'nt，該式滿足梁兩端的邊界條件。其中ω'n為考慮剪切變形及轉動慣量影響的梁自由振動頻率，相應地，(4)式中的ωn為不考慮剪切變形及轉動慣量影響的梁自由振動頻率。定義Ωn=ω'n/ωn，則梁的頻率方程為:

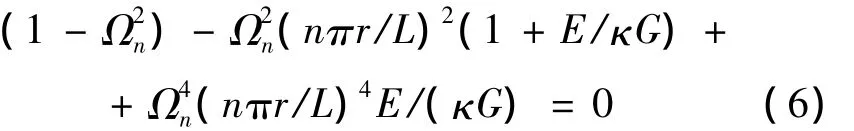
如果假定nr/L≤1，則方程(6)中含(nπr/L)4的項可忽略不計。故考慮剪切變形及轉動慣量影響的等截面簡支直梁的自由振動頻率為:

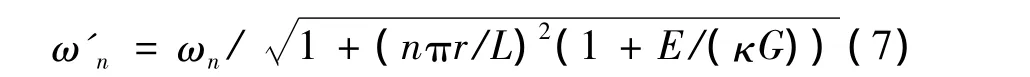
由(7)式可見:ω'n＜ωn。分母中的項(nπr/L)代表由轉動慣量產生的修正項，(nπr/L)2(E/(κG))則代表由剪切變形產生的修正項。顯然，長細比L/r越小，剪切變形及轉動慣量對頻率的影響越顯著。

3 H型鋼簡支梁自由振動頻率計算

H型鋼是世界各國廣泛使用的熱軋型鋼，與普通工字鋼相比，其翼緣內外兩側平行，便于同其他構件連接，目前在鋼結構設計中正逐步替代普通工字鋼。熱軋 H型鋼有3種類別，即 HW，HM和HN。從每一種類別中分別選出1種典型型號，具體型號及截面參數見表1。表1中剪應力不均勻系數κ根據公式κ=Aweb/A近似計算得出，其中Aweb為H型鋼截面的腹板面積，A為H型鋼截面的全截面面積。

鋼結構設計中，H形鋼梁的設計長細比L/r在20 ～50 之間，故計算中共考慮 20，25，30，35，40，45和50共7種長細比。此外，鋼材的彈性模量E=2.06×1011N/m2，剪切模量 G=0.79 ×1011N/m2。將上述參數分別代入式(4)及式(7)，可計算出初等梁理論和考慮剪切變形及轉動慣量影響的高等梁理論的簡支梁自由振動頻率。計算所得前3階頻率下的自由振動頻率分別見表2～4。

由表2～4可見:隨著H型鋼梁長細比的增大，根據初等梁理論計算得到的簡支梁自由振動頻率相對高等梁理論計算得到的簡支梁自由振動頻率的誤差逐漸減小。為了能夠更加直觀地比較2種梁理論在自由頻率計算結果上的差異，下面將表2～4中所列各階頻率描繪成圖，見圖1～3。

如圖1～3所示，圖例中的A型梁代表HW200×200×8×12，B型梁代表HM300×200×8×12，C型梁代表HN400×200×8×13。

表1 典型熱軋H型鋼型號及截面參數［10］Table 1 Typical hot－rolled H－shape steel models and parameters

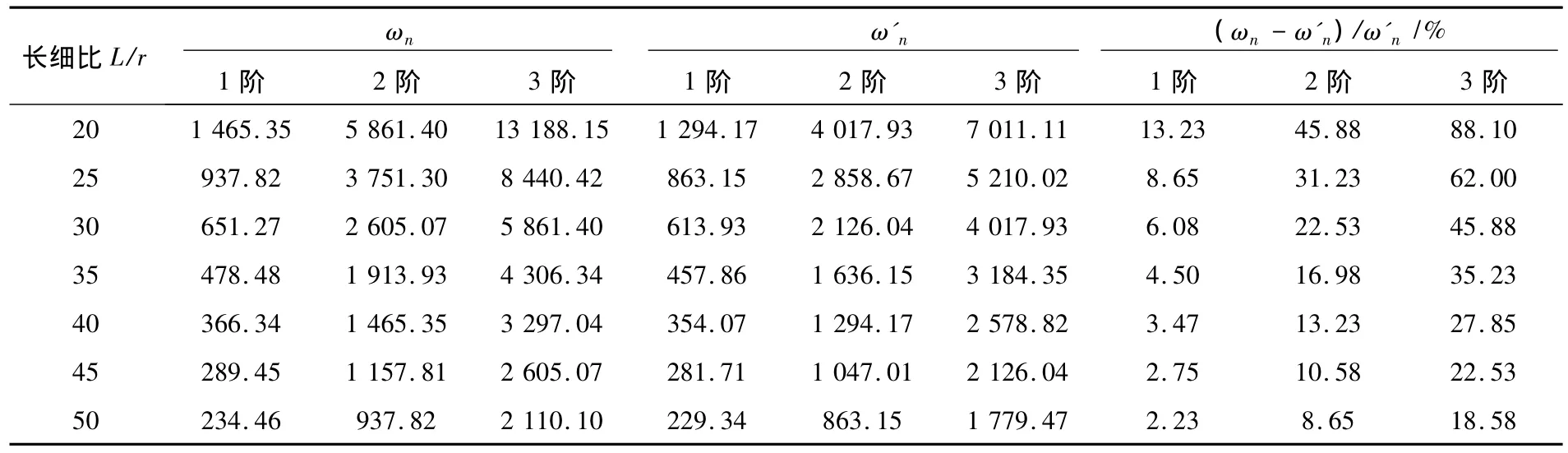
表2 H型鋼簡支梁自由振動頻率(HW200×200×8×12)Table 2 Free vibration frequency of H－shape steel beam(HW200×200×8×12)

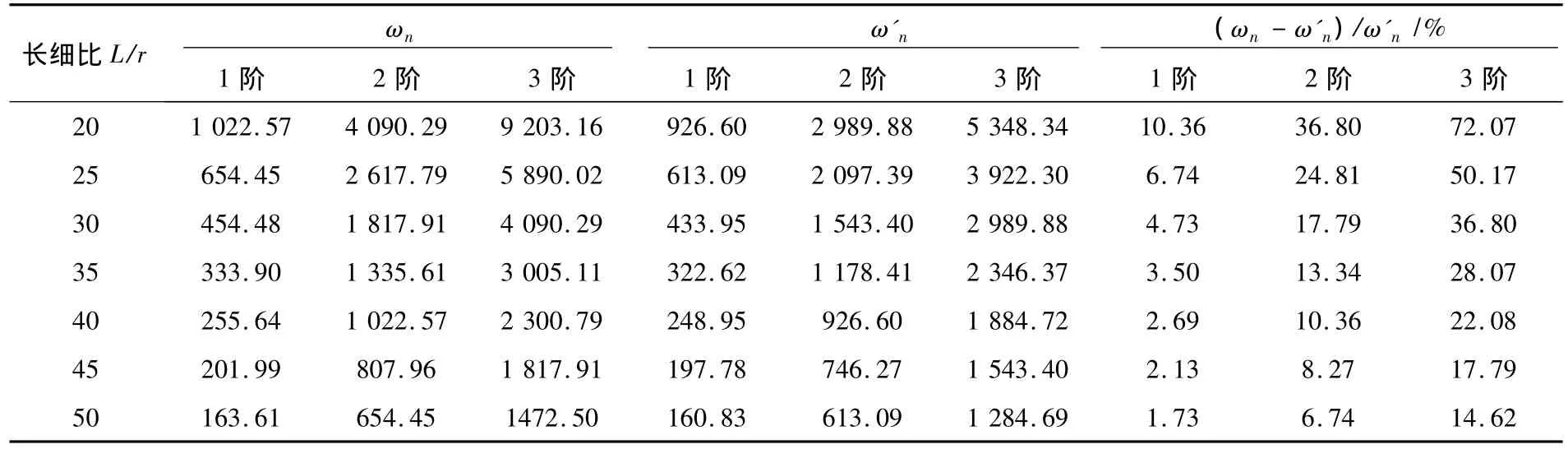
表3 H型鋼簡支梁自由振動頻率(HM300×200×8×12)Table 3 Free vibration frequency of H－shape steel beam(HM300×200×8×12)

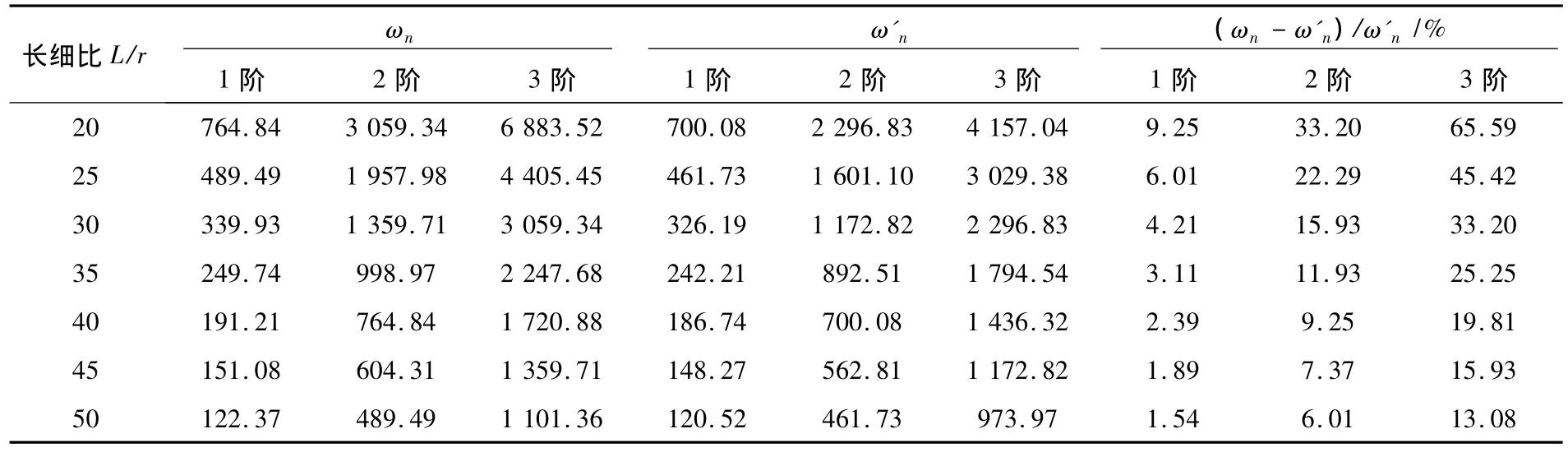
表4 H型鋼簡支梁自由振動頻率(HN400×200×8×13)Table 4 Free vibration frequency of H－shape steel beam(HN400×200×8×13)

4 計算結果分析

由表2～4及圖1～3可知:隨著長細比的增大，采用初等梁理論計算的自由振動頻率的誤差逐漸減小;低階頻率的誤差小于高階頻率的誤差。另一方面，由表1可見:HW型鋼的剪應力不均勻系數κ小于HN型鋼的剪應力不均勻系數，而κ越小，在式(7)中由剪切變形產生的修正項對頻率計算精度的影響越顯著。因此，在同樣的長細比下，HW型鋼簡支梁頻率的計算誤差最大，HN型鋼簡支梁頻率的計算誤差最小。

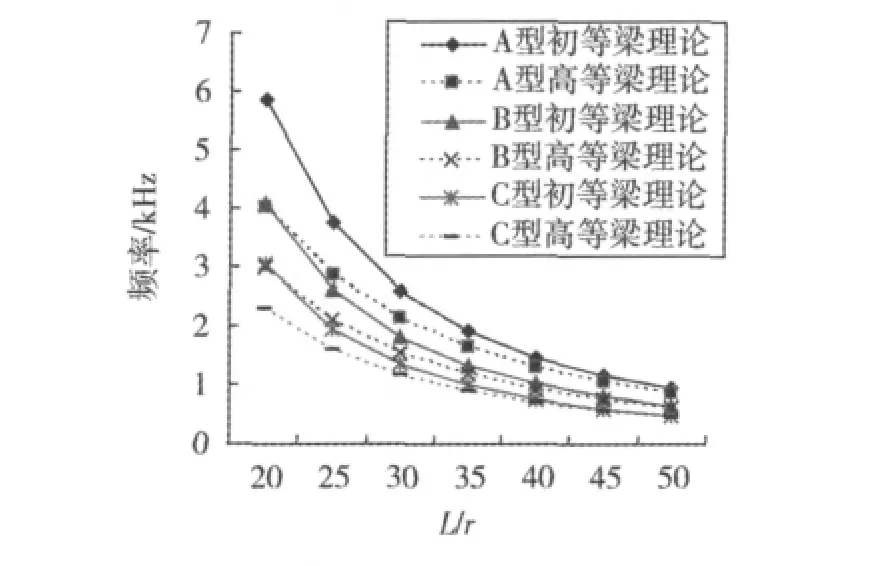
圖2 H型鋼梁第2階頻率Fig.2 2nd frequencies of H －shape steel beam

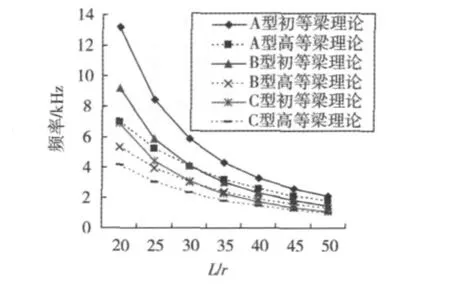
圖3 H型鋼梁第3階頻率Fig.3 3rd frequencies of H －shape steel beam

對于HW200×200×8×12簡支梁的1階頻率，當長細比大于等于35時，初等梁理論計算結果的誤差小于5%，精度可以滿足工程要求;但對于其第2階、第3階頻率，初等梁理論的計算誤差均大于5%。

對于HM300×200×8×12簡支梁的1階頻率，當長細比大于等于30時，初等梁理論計算結果誤差小于5%，精度可以滿足工程要求;但對于其第2階、第3階頻率，初等梁理論的計算誤差均大于5%。

對于HN400×200×8×13簡支梁的1階頻率，當長細比大于等于30時，初等梁理論計算結果的誤差小于5%，精度可以滿足工程要求;但對于其第2階、第3階頻率，初等梁理論的計算誤差均大于5%。這說明采用初等梁理論求解簡支梁的高階頻率，其計算精度通常難以滿足工程設計要求。

5 結論

(1)對于各種H型鋼截面簡支梁的第1階頻率，當長細比大于30時(HM截面為35)，采用初等梁理論得到的計算結果的誤差在5%以內，可滿足工程需要。

(2)對于各種H型鋼截面簡支梁的第2階及更高階頻率，在常用長細比范圍內，采用初等梁理論得到的計算結果的誤差均超過5%以內，不能滿足工程要求。

(3)在計算長細比較小的“短梁”的第1階頻率或各種長細比H型鋼截面簡支梁的高階頻率時，必需采用求解精度更高的考慮剪切變形與轉動慣量影響的高等梁理論模型，計算結果方可用于工程分析或動力設計。

［1］許醇義.剪切變形和轉動慣量對梁自由振動的影響［J］.蘇州城建環保學院學報，1996，9(3):30－33.XU Chun－yi.Rotatory inertia on the free vibration of a beam［J］.Journal of Suzhou Institute of Urban Construction and Environmental Proteotion，1996，9(3):30 －33.

［2］李進軍，李國強.考慮軸力和剪切變形影響的楔形梁自由振動分析［J］.鋼結構，2000，15(1):31－34.LI Jin－jun，LI Guo－qiang.Anslysis of free vibration for tapered beam including effects of axial force and shear deformation［J］.Steel Construction，2000，15(1):31 －34.

［3］樓夢麟，任志剛.Timoshenko簡支梁的振動模態特性精確解［J］.同濟大學學報，2002，30(8):911－916.LOU Meng－lin，REN Zhi－gang.Precise solution to modal characteristics of Timoshenko Pin －ended beams［J］.Journal of Tongji University，2002，30(8):911 －916.

［4］龔善初.軸向荷載、轉動慣量和剪切變形對簡支梁固有頻率的影響［J］.河南科學，2004，22(5):592－596.GONG Shan－chu.The influence of axial load moment of intertia and shear deformation of the natural freauency of simply supported beam［J］.Henan Science，2004，22(5):592－596.

［5］馬連生，歐志英.經典理論與一階理論之間簡支梁特征值的解析關系［J］.應用力學學報，2006，23(3):447－450.MA Lian－sheng，OU Zhi－ying.Analytical relationships of eigenvalue for a simply supported beam between EBT and TBT［J］.Chinese Journal of Applied Mechanics，2006，23(3):447－450.

［6］王力力，易偉健，何慶峰.考慮剪切變形和轉動慣量影響的梁的固有頻率計算［J］.鐵道科學與工程學報，2007，4(5):6 －10.WANG Li－li，YI Wei－jian，HE Qing－feng.Eigenfrequencies of beams considering the effects of shear distortion and rotary inertia［J］.Journal of Railway Science and Engineering，2007，4(5):6 －10.

［7］葛素娟，李靜斌.簡支梁橫向振動固有頻率的誤差分析［J］. 鄭州大學學報:工學版，2010，31(5):48 －51.GE Su－juan，LI Jing－bin.Error anslysis of transverse vibration natural frequency of simply supported beam［J］.Journal of Zhengzhou University:Engineering Science，2010，31(5):48 －51.

［8］Chopra A K.結構動力學理論及其在地震工程中的應用［M］.謝禮立，呂大剛，等譯.北京:高等教育出版社，2007.Chopra A K.Dynamics of structures－theory and applications to earthquake engineering［M］.XIE Li－li，Lü Dagang，translate.Beijing:Higher Education Press，2007.

［9］王 偉，賴永星，苗同臣，等.振動力學與工程應用［M］.鄭州:鄭州大學出版社，2008.WANG Wei，LAI Yong－xing，MIAO Tong－chen，et al.Vibration mechanics and engineering application［M］.Zhengzhou:Zhengzhou University Press，2008.

［10］GB/T 11263—2010，熱軋H型鋼和剖分 T型鋼［S］.GB/T 11263—2010，Hot－rolled H and cut T section steel［S］.