一個(gè)新的超混沌系統(tǒng)及其電路實(shí)現(xiàn)*
申朝文,禹思敏
(①?gòu)V東工業(yè)大學(xué) 自動(dòng)化學(xué)院,廣東 廣州 510006;②仲愷農(nóng)業(yè)工程學(xué)院 信息學(xué)院,廣東 廣州 510225)
0 引言
近年來(lái),隨著混沌系統(tǒng)理論的不斷完善,越來(lái)越多的研究表明,超混沌系統(tǒng)與一般混沌系統(tǒng)相比具有更為復(fù)雜的拓?fù)浣Y(jié)構(gòu)和動(dòng)力學(xué)行為,它能在混沌保密通信和混沌信息加密上提供更為可靠的保證,具有較好的工程應(yīng)用前景。因此,越來(lái)越多的研究者在現(xiàn)有混沌系統(tǒng)上進(jìn)行改造,提出了一系列的超混沌系統(tǒng)[1-5],以及如何構(gòu)建超混沌系統(tǒng)的方法。可見(jiàn)對(duì)超混沌的研究已經(jīng)成為了混沌應(yīng)用領(lǐng)域中一個(gè)重要的研究熱點(diǎn)。
1 新的四維超混沌系統(tǒng)
文獻(xiàn)[6]給出了一個(gè)新的三維二次多項(xiàng)式自治系統(tǒng),其無(wú)量綱方程為:

當(dāng)a=20,b=5,c=10,d=7時(shí),系統(tǒng)(1)處于混沌狀態(tài)。3個(gè)Lyapunov指數(shù)分別為:,系統(tǒng)的3個(gè)平衡點(diǎn)為:平衡點(diǎn)O的特征值為:= 10,= 10,= -5,平衡點(diǎn) E1和 E2處的特征值為=-1 8.2601,=-1.63±10.3379i。因此,系統(tǒng)(1)具有一個(gè)鞍點(diǎn)和兩個(gè)穩(wěn)定的鞍焦平衡點(diǎn)。
要產(chǎn)生超混沌系統(tǒng)必須滿足兩個(gè)必要條件:①對(duì)于自治系統(tǒng)而言,至少是四維;②至少有兩個(gè)正的Lyapunov指數(shù)且所有Lyapunov指數(shù)之和小于零。根據(jù)以上兩個(gè)條件,在系統(tǒng)(1)的基礎(chǔ)上引入一個(gè)反饋控制器u,令u的變化速率為d/dueyτ=-,并把控制器u反饋到系統(tǒng)(1)的第二個(gè)方程中,構(gòu)造出一個(gè)可產(chǎn)生超混沌現(xiàn)象的四維自治系統(tǒng),其狀態(tài)方程為
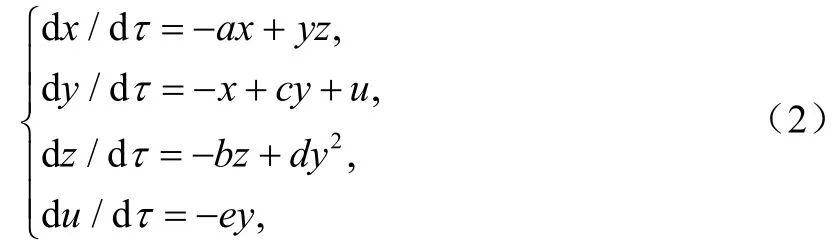
當(dāng) a = 20,b =5,c = 10,d =7,e = 13.5,系統(tǒng)(2)的4個(gè) Lyapunov指數(shù)分別為=2.2259,=0.2069,=0,=-34.9259,有兩個(gè)正的Lyapunov指數(shù),系統(tǒng)處于超混沌狀態(tài),對(duì)應(yīng)的幾個(gè)典型的超混沌吸引子相圖如圖1所示。

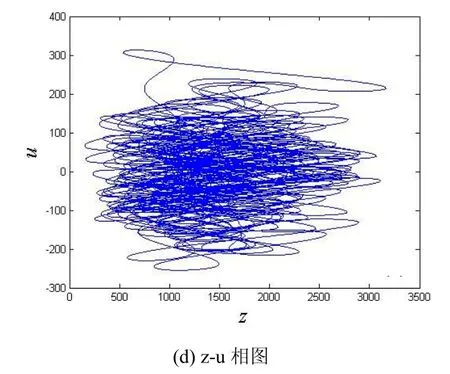
圖1 超混沌吸引子相圖
2 新超混沌系統(tǒng)的動(dòng)力學(xué)分析
2.1 系統(tǒng)的耗散性
2.2 平衡點(diǎn)分析
令 系 統(tǒng)(2)的 每 一 個(gè) 方 程dx/dτ =dy/dτ =得系統(tǒng)平衡狀態(tài)方程為:

由式(3)計(jì)算得,系統(tǒng)(2)有唯一平衡點(diǎn))0000(,,,O,它與系統(tǒng)參數(shù)的取值無(wú)關(guān),在平衡點(diǎn)O處線性化系統(tǒng)(2),得到對(duì)應(yīng)的Jacobian矩陣為:
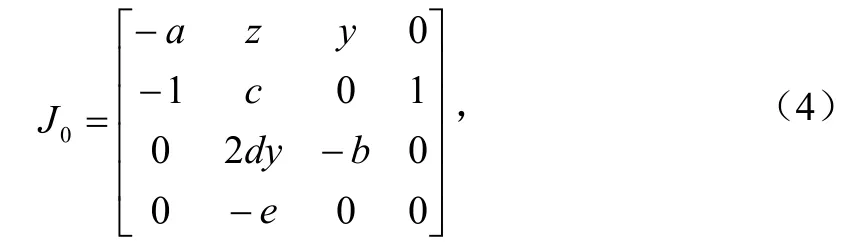
取系統(tǒng)(2)參數(shù) a = 5 0,b = 7 .5,c = 2 5,d = 7 .5,e =13.5時(shí),計(jì)算出平衡點(diǎn)O處的特征值為= 0.5522,= 24.4478,=-50,= -7.5,因此O是一個(gè)不穩(wěn)定的鞍點(diǎn)。
2.3 Lyapunov指數(shù)譜圖與分岔圖分析
隨著系統(tǒng)參數(shù)的改變,系統(tǒng)平衡點(diǎn)的穩(wěn)定性將會(huì)發(fā)生變化,從而系統(tǒng)也將處于不同的狀態(tài)。固定參數(shù) a =50, b=7.5,c=25,d =7.5,使參數(shù)e在(0,90]之間變化,系統(tǒng)初始值取(1,2,500,4),隨參數(shù)e變化的Lyapunov指數(shù)譜和變量x的分岔圖分別如圖2和圖3所示。需要說(shuō)明,圖2中并未給出始終處于最大負(fù)值的Lyapunov指數(shù)。
從圖2可以看出,當(dāng)e∈(0,0.3)時(shí),系統(tǒng)的Lyapunov指數(shù)都小于或等于零,系統(tǒng)處在周期態(tài)或擬周期態(tài)。e ∈ [0 .3,0.7)時(shí),系統(tǒng)存在一個(gè)正的Lyapunov指數(shù),系統(tǒng)處于混沌狀態(tài);而e∈[0.7,50.4]時(shí),系統(tǒng)有兩個(gè)正的 Lyapunov指數(shù),系統(tǒng)處于超混沌狀態(tài)。當(dāng)e∈(5 0.4,74.3]時(shí),系統(tǒng)至少有一個(gè)正的Lyapunov指數(shù),系統(tǒng)在混沌態(tài)和超混沌態(tài)來(lái)回轉(zhuǎn)換,形成復(fù)雜的動(dòng)力學(xué)行為。當(dāng) e ∈(7 4.3,79.7]時(shí),系統(tǒng)有一個(gè)正的Lyapunov指數(shù)或者最大的Lyapunov指數(shù)為零,系統(tǒng)處在混沌態(tài)或復(fù)雜周期態(tài)。當(dāng)e∈(79.7,90]時(shí),系統(tǒng)處在擬周期態(tài)或周期態(tài)。隨著e的繼續(xù)增加,最大Lyapunov指數(shù)趨近于零,意味著系統(tǒng)的解最終演化為一個(gè)周期軌。
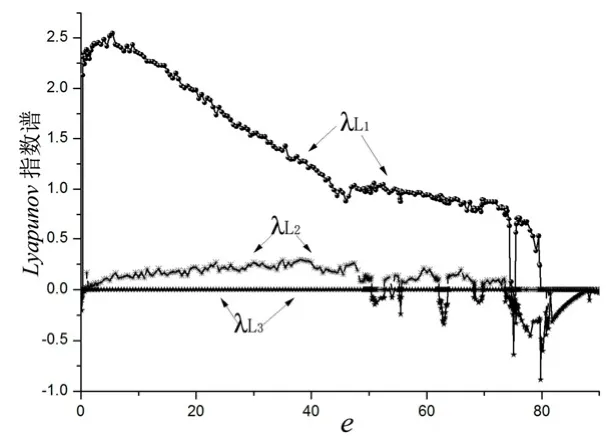
圖2 Lyapunov指數(shù)譜
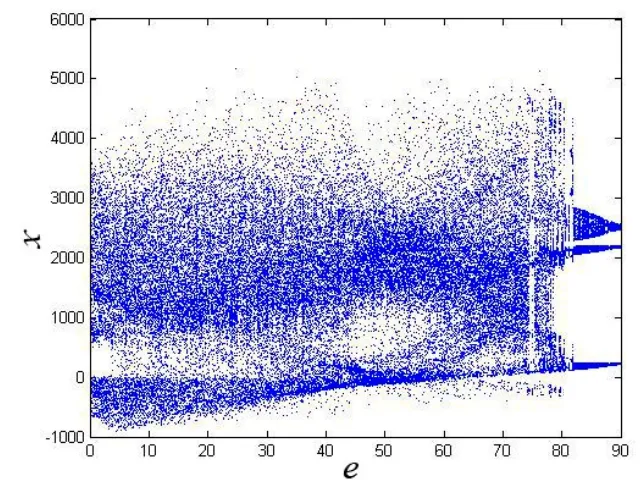
圖3 系統(tǒng)分岔
3 超混沌系統(tǒng)的電路設(shè)計(jì)與實(shí)現(xiàn)
根據(jù)式(2)設(shè)計(jì)實(shí)現(xiàn)該四維超混沌系統(tǒng)功能的實(shí)際電路[7-8],采用線性電阻,線性電容,運(yùn)算放大器為AD712,由于系統(tǒng)存在非線性項(xiàng),可選用乘法器AD633實(shí)現(xiàn)。必須注意的是,變量 x , y ,z,u各自的動(dòng)態(tài)范圍大約[-4000,4000],[-1 00,100],[100,3200],[-2 50,320]。遠(yuǎn)大于運(yùn)算放大器的飽和電壓,故必須進(jìn)行變量比例壓縮變換,才便于電路實(shí)現(xiàn)。對(duì)系統(tǒng)(2)進(jìn)行非均勻變量比例壓縮變換,令x, y ,z,u 壓縮到原來(lái)的 1 / 1000,1/20,1/1000,1/100,由于系統(tǒng)變量的變換不影響系統(tǒng)的狀態(tài)及性能,從而系統(tǒng)(2)可變?yōu)椋簩?shù) a =50, b=7.5,c=25,d =7.5,e =13.5代入式(5),并作時(shí)間尺度變換,令 τ =,= 100,得:
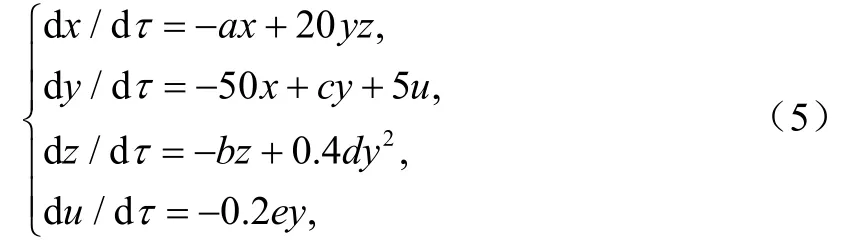
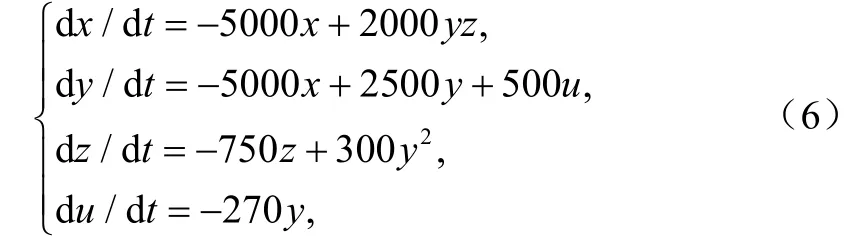
對(duì)式(6)進(jìn)行模塊化電路設(shè)計(jì),如圖4所示。
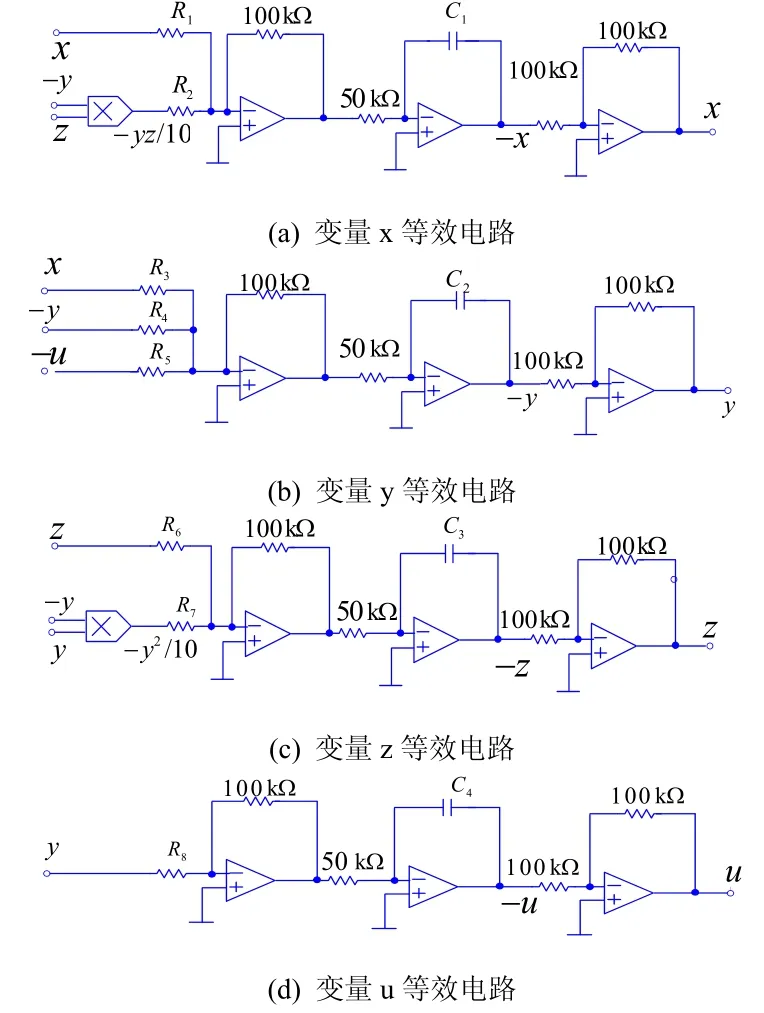
圖4 超混沌電路設(shè)計(jì)
電路的狀態(tài)方程為:

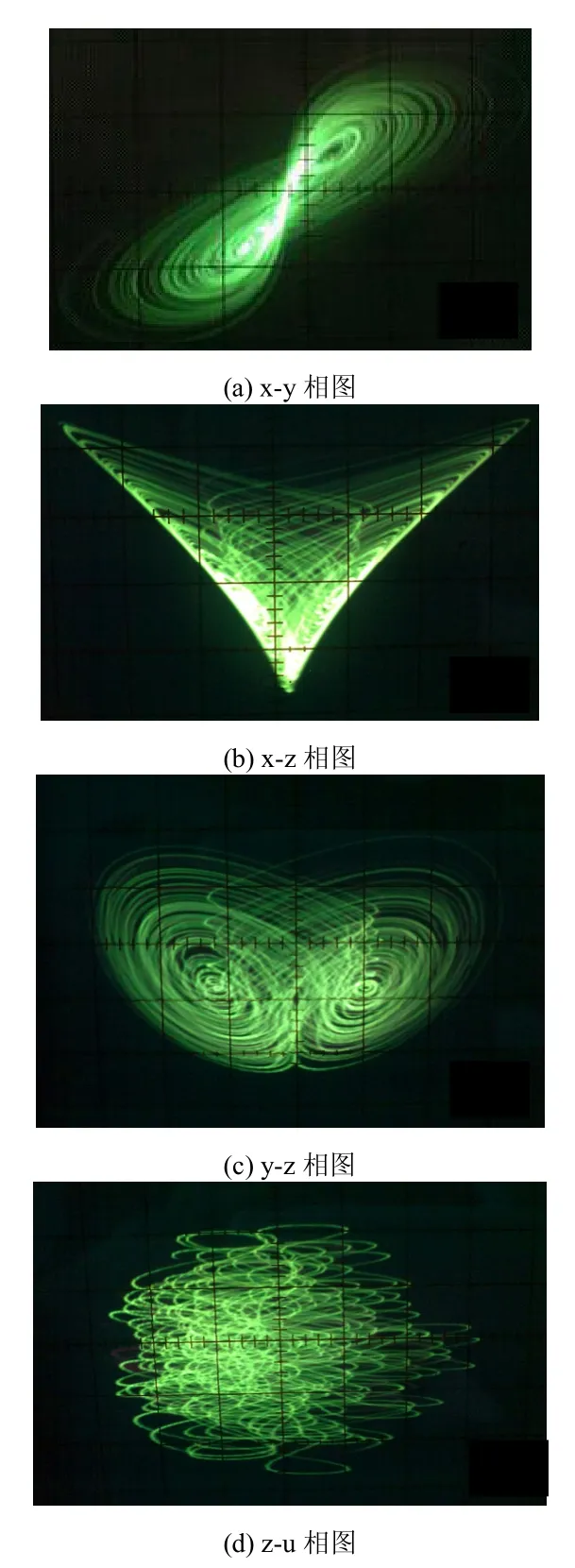
圖5 電路實(shí)現(xiàn)超混沌吸引子相圖
4 結(jié)語(yǔ)
通過(guò)對(duì)一個(gè)三維二次自治系統(tǒng)中引入一個(gè)變量反饋控制器,構(gòu)造出一個(gè)新的超混沌系統(tǒng),對(duì)系統(tǒng)的動(dòng)力學(xué)特性進(jìn)行了相關(guān)的理論分析與數(shù)值仿真,可以得出該系統(tǒng)與其他超混沌系統(tǒng)相比[9-10],具有較大的正李雅普諾夫指數(shù),且在較廣的動(dòng)態(tài)參數(shù)范圍內(nèi)存在超混沌軌道。最后設(shè)計(jì)并實(shí)現(xiàn)了該超混沌系統(tǒng)的硬件電路,給出了相關(guān)電路的實(shí)驗(yàn)結(jié)果,證實(shí)該超混沌系統(tǒng)具有較為復(fù)雜的拓?fù)浣Y(jié)構(gòu),在混沌保密通信等領(lǐng)域具有潛在的應(yīng)用前景。
[1] CHEN Z,YANG Y,QI G, et al. The Generation and Circuit Implementation of a New Hyper-chaos based upon Lorenz System[J].Physics.Letter.A,2007(361):78-86.
[2] 王光義,鄭艷,劉敬彪. 一個(gè)超混沌 Lorenz吸引子及其電路實(shí)現(xiàn)[J]. 物理學(xué)報(bào),2007,56(06):3313-3320.
[3] 滿峰泉,侯承璽.一個(gè)新的超混沌系統(tǒng)設(shè)計(jì)與實(shí)現(xiàn)[J].通信技術(shù),2010,43(11):108-111.
[4] 劉揚(yáng)正.超混沌 Lü 系統(tǒng)的電路實(shí)現(xiàn)[J].物理學(xué)報(bào),2008,57(11):1439-1443.
[5] BAO B. Hyperchaos from an Augmented Lü System[J].Int.J. Bifurcation and Chaos,2010,20(11):3689-3698.
[6] 禹思敏.混沌系統(tǒng)與混沌電路—原理、設(shè)計(jì)及其在通信中的應(yīng)用[M].西安:西安電子科技大學(xué)出版社,2011.
[7] 包伯成,劉中,許建平.一類超混沌系統(tǒng)電路實(shí)現(xiàn)及其動(dòng)力學(xué)分析[J].四川大學(xué)學(xué)報(bào),2010,42(02):182-187.
[8] 謝國(guó)波,禹思敏,周武杰.一個(gè)新的三維二次自治混沌系統(tǒng)及其研究[J].通信技術(shù),2009,42(01):267-270.
[9] 黃愛(ài)美,李欣,馬寶艷. 基于二維超混沌序列的交替加密[J].信息安全與通信保密,2007(01):125-126,130.
[10] 張輝,陳建國(guó).嵌套混沌變參映射的構(gòu)造及分析[J].信息安全與通信保密, 2008(07):51-52,55.

