一種基于對角載入的魯棒MVDR波束形成算法＊

施榮華，孟秋杰，董 健，郭 迎

（中南大學 信息科學與工程學院，湖南 長沙 410083）

自適應波束形成廣泛地應用于雷達、系統識別、聲納和移動通信等領域[1－5].MVDR自適應波束形成器在保持信號不變的約束下使噪聲輸出功率最小，具有良好的弱信號檢測和高分辨力性能，因此得到廣泛的應用.但是由于外部環境、信源、傳感器陣列等諸多條件的復雜變化，導致信號方向向量出現偏差，使傳統的MVDR波束形成算法的性能下降.為了克服各種誤差引起的性能下降，一些學者近幾十年進行了大量研究來提高自適應波束形成的穩健性，其中最具代表性的方法有3種：特征空間（ESB）法、線性約束（LCMV）法和對角加載（LSMI）法.特征空間法[6]具有較快的收斂速度，但它需要準確估計信號子空間維數，當子空間維數過估計或欠估計時算法失效；線性約束法[7]通過適當的約束條件使得自適應波束滿足一定的穩健條件，但只適用于觀察方向失配的情況；對角加載法：文獻[8]對協方差矩陣沿其對角線加一正常數后再用采樣協方差矩陣求逆方法求得自適應權值提高自適應波束形成器的穩健性.由于加載量被固定，不隨期望信號的信噪比和導向矢量的誤差變化而變化，當信噪比增加時，輸出信干噪比會明顯惡化.文獻[9]采用最差性能最優化思想，提高了波束形成器的魯棒性，但是該算法計算復雜度高，不便于工程實現；文獻[10]采用矩陣錐消方式，通過對協方差矩陣點乘一個給定誤差范圍，提高波束形成器的穩健性，但是由于給定的誤差范圍不好控制，效果并不理想.

本文考慮到方向向量最大允許偏差的情況，提出了一種新的基于對角載入的MVDR自適應波束形成算法.由于該算法是在最差性能下的優化問題，因此在一定范圍內，對角加載量的大小對該算法的性能影響不大；同時在求解過程中進行降維處理，避免矩陣求逆，大大地降低運算量，便于工程實現.仿真實驗驗證了所提魯棒算法的有效性和可行性.

1 傳統算法描述

1.1 信號模型

考慮M元各向同性的均勻線陣，陣元間距為d，期望信號波達方向為θ0，有D－1個干擾源，波達方向分別為 ｛θ1，θ2，...，θD－1｝，其中，M ＞D .以陣列的第1個陣元為基準，各個窄帶信號在基準陣元的復包絡分別為s0（t），s1（t），...，sD－1（t），則第l個陣元端接收的信號為：

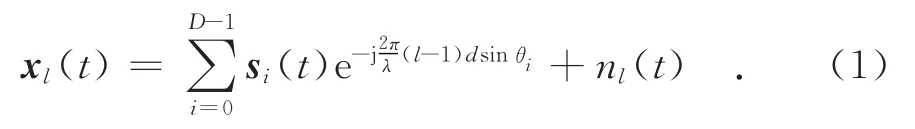
式中：λ為信號的波長；nl（t）為第l個陣元上均值為零、方差為σ2n的白噪聲.天線陣列的接收向量[11]為：

式中：a（θi）為到達方向為θi的信號對應的導向矢量.陣列輸出為：

陣列輸出的信干噪比為：

式中：Rs為陣列期望信號的協方差矩陣，Ri＋n為干擾和噪聲的協方差矩陣.

在信號處理中，為保證期望信號正常接收，應盡量減弱和抑制干擾信號，即增大系統的輸出信干噪比.在自適應陣列天線系統中，通過調整權重向量，可使系統的輸出信干噪比達到最優值，即：

式中：σ2s為信號的功率.式（5）給出了式（4）的輸出信干噪比SINR的上限.

1.2 MVDR波束形成算法

MVDR波束形成器是使噪聲以及來自非θ方向的任何干擾的功率為最小，但又能保持在觀測方向θ上的信號功率不變，其代價函數為：

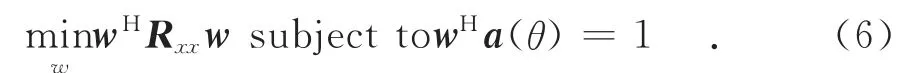
式中：a（θ）為期望信號的方向向量.令

求式（7）的梯度并令其為零，得到：

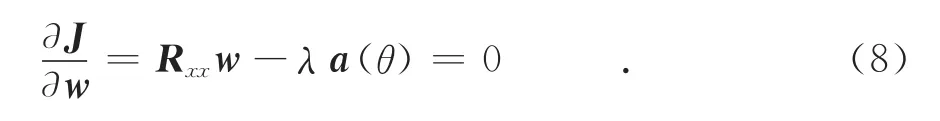
解得權重向量為：

把式（9）代入式（6）的約束條件中，求得：

把式（10）代入式（9）中求出最優權重向量

MVDR算法要求準確知道信號的方向向量，而在實際應用環境中，由于信號的方向向量存在偏差，這使得自適應算法的性能下降，輸出的信干噪比偏離最優值.MVDR波束形成器，不能有效地抑制干擾，產生嚴重的信號相消現象.

2 魯棒MVDR波束形成算法

針對信號的方向向量誤差導致傳統MVDR算法的性能下降，本文提出了基于對角載入的魯棒MVDR波束形成算法.該算法考慮信號方向向量的偏差對MVDR算法性能的影響，通過對協方差矩陣進行修正，得到最優的權重向量，有效地抑制了偏差對輸出性能的影響，具有很強的魯棒性.

假設信號方向向量的偏差為Δ，ε為最大偏移量：

那么信號的實際方向向量屬于集合：

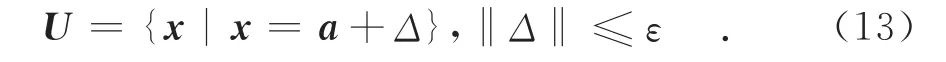
在觀測信號方向上無失真響應的絕對值不小于1.

把式（14）的不等式約束轉化為等式約束[11]的形式可得：

則式（6）可寫為

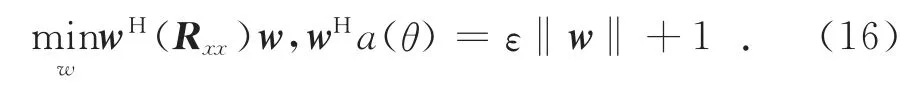
進一步得到代價函數為：

對代價函數式（17）的求解，本文將其轉化為兩個最優化問題.首先求其子函數的最大值：

利用拉格朗日方法求得：

將式（19）代入式（18）中得到：

然后求代價函數的最小值，代價函數式（17）可以重寫為

其中：a（θ）為期望信號的方向向量.令

其中：λ為拉格朗日因子，對式（22）求梯度

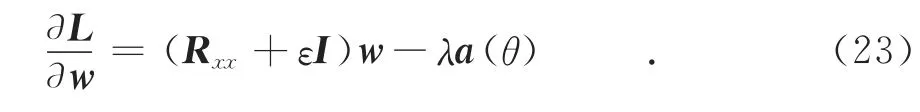
令其梯度等于零等到最優權向量

權重向量是通過對矩陣直接求逆得到的最優值，其計算量會隨著陣元數目和采樣數目的增加而劇增.本文采用遞推算法，避免矩陣直接求逆，將計算復雜度從多維降到一維.利用式（17）得到基于對角載入的魯棒MVDR算法的遞推公式為

其中：μ為步長因子，將式（25）代入式（21）的約束條件，得到：

通過求解式（26）得到拉格朗日因子λ為：

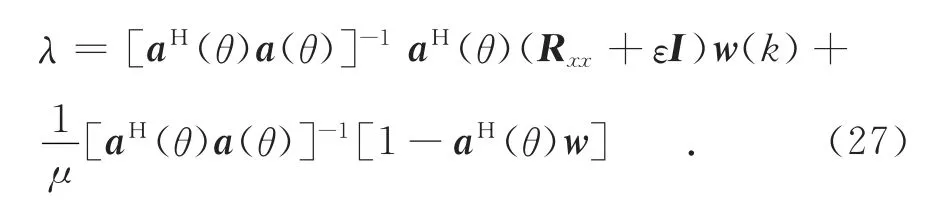
代入求得最優權向量公式為：

其中：

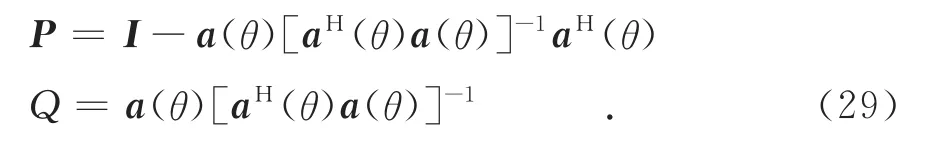
從式（28）中可見，最優權向量的計算復雜度為一維，便于工程實現.

3 仿真實驗結果

實驗考慮10個陣元的等距線陣，陣元間距為半個波長，采樣次數為4 096，對于每一點都分別進行100次的仿真實驗.假設期望信號的波達方向為0°，兩個干擾源的波達方向分別為30°和50°.

實驗一 陣列方向圖的比較

設仿真條件為：SNR＝10dB，對角載入因子為ε＝2，信號的實際波達方向為2°，即偏差為2°.圖1給出了方向向量無偏差情況下兩種算法在信號波達方向上形成的陣列方向圖.圖中垂直的點劃線表明了信號的實際波達方向.從圖1中可以看出，本文算法在期望信號處形成了很高的增益，達到了提取有用信號的目的.圖2給出了方向向量存在偏差時的陣列方向圖，為了便于觀察，仿真時將本文算法的輸出曲線垂直下移.從圖2中可以看出，傳統MVDR算法在有用信號處形成零陷，而本文所提的算法在存在偏差的情況下也有很強的增益，避免了信號相消現象，對信號方向向量偏差的敏感度較低，具有很好的魯棒性.

在工程實現中，方向向量最大允許偏差的值一般不會超過2°，本文選取2°偏差進行仿真實驗，仿真結果說明該算法具有很好的輸出性能，因此該算法具有一定的適用性.

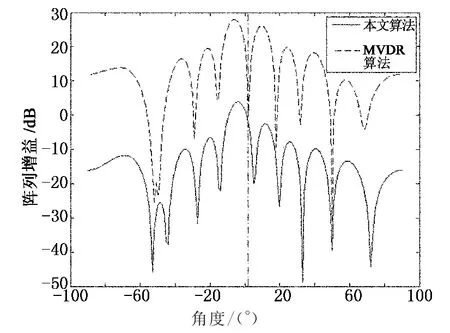
圖1 兩種算法陣列方向圖（無偏差）Fig.1 Array pattern of the two algorithms（no deviation）

圖2 兩種算法陣列方向圖（2°偏差）Fig.2 Array pattern of the two algorithms（2°deviation）

實驗二 輸出信干噪比SINR的比較

設仿真條件為：信噪比SNR＝10dB，信號的實際波達方向為2°，即偏差為2°.圖3給出了無偏差情況下陣列輸出的信干噪比SINR隨采樣數目的變化曲線.圖4給出了存在2°偏差的情況下陣列輸出的信干噪比SINR隨采樣數目的變化曲線.

從本實驗中可以看出，與傳統的MVDR算法相比，本文所提的算法對信號方向向量的偏差具有很強的魯棒性，輸出的信干噪比SINR要明顯優于傳統的MVDR算法.

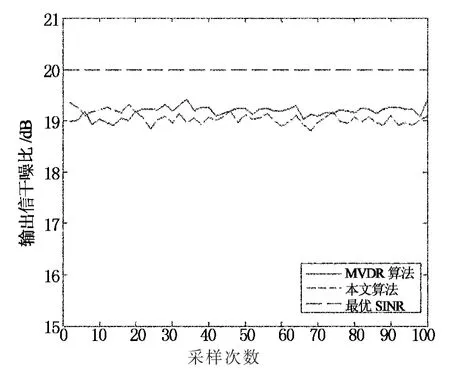
圖3 陣列輸出的信干噪比（無偏差）Fig.3 Output SINR of the two algorithms（no deviation）

圖4 陣列輸出的信干噪比（2°偏差）Fig.4 Output SINR of the two algorithms（2°deviation）

實驗三 不同對角載入因子的比較

設仿真條件為：信噪比SNR＝10dB，信號的實際波達方向為2°，即偏差為2°.圖5給出了ε＝2和ε＝4兩種不同對角載入因子情況下所提算法的陣列方向圖，圖6給出了對角載入因子分別為ε＝2和ε＝1.5情況下所提算法的陣列方向圖.

綜合圖5和圖6可以看出，本文算法在選取不同對角載入因子ε＝1.5，ε＝2，ε＝4時，對于方向向量偏差均具有較強的魯棒性；這說明，在一定范圍內對角載入因子的不同取值對本文算法的性能影響不大.

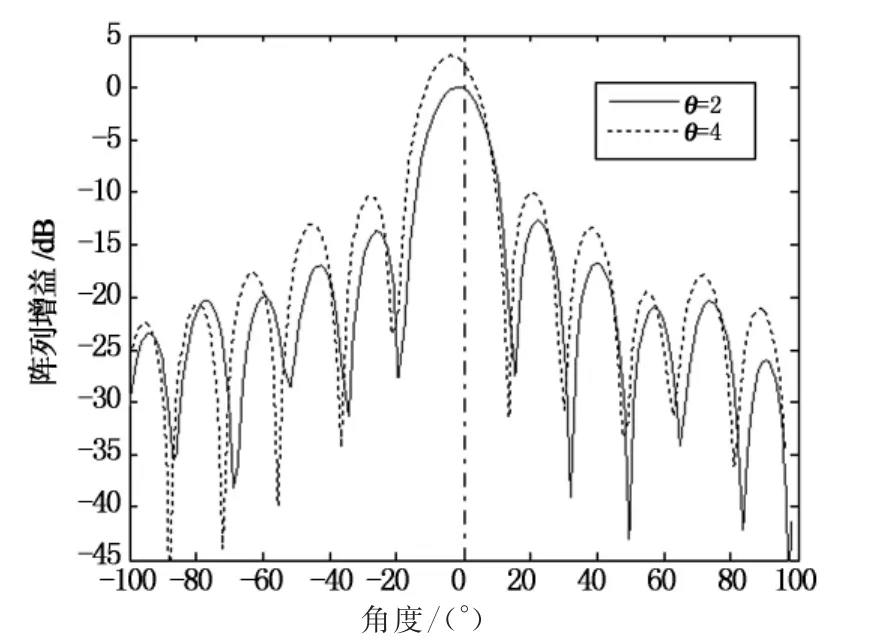
圖5 對角載入因子ε＝2和ε＝4Fig.5 Array pattern of the diagonal factor between 2and 4

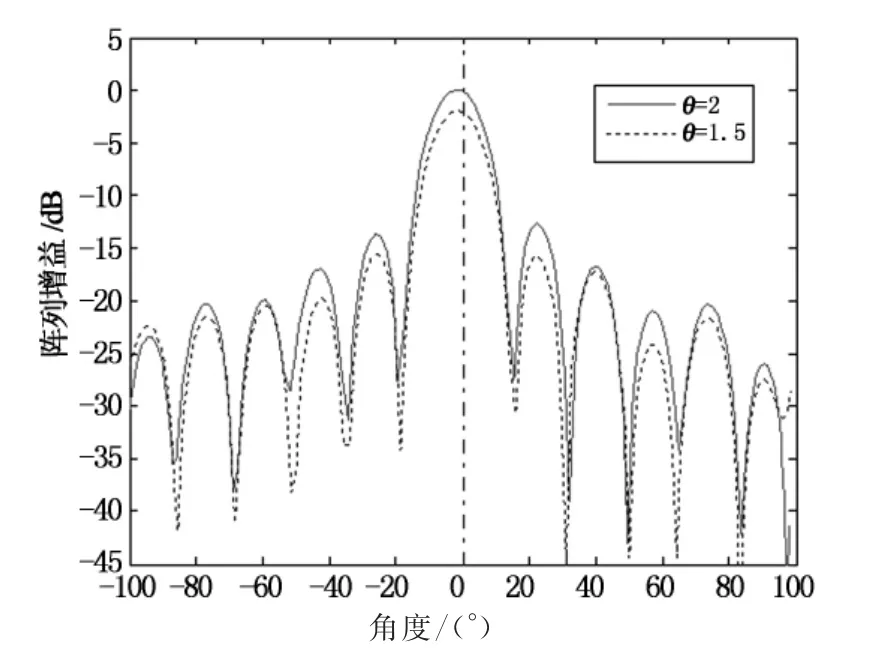
圖6 對角載入因子ε＝2和ε＝1.5Fig.6 Array pattern of the diagonal factor between 2and 1.5

4 結 論

針對方向向量存在偏差時所導致傳統MVDR波束形成器性能急劇下降的問題，本文提出了一種基于對角載入的魯棒MVDR波束形成算法.該算法對協方差矩陣的估計誤差進行約束，提高了算法的穩健性；在求解過程中進行降維處理，降低了計算量，易于實時實現.該算法有效地抑制了方向向量偏差對MVDR波束形成器輸出性能的影響，具有較強的魯棒性.仿真實驗表明：與傳統MVDR算法相比，所提算法具有更好的輸出性能，在一定范圍內對角載入因子的取值對所提算法的性能影響不大.

[1] KROLIK J L.The performance of matched－field beamformers with Mediterranean vertical array data[J].IEEE Trans Signal Processing，1996，44（10）：2605－2611.

[2] 曾凡仔，陳苗苗，羅娟，等.一種能量有效的無線傳感網絡節點跟蹤算法[J].湖南大學學報：自然科學版，2009，36（1）：81－84.ZENG Fan－zai，CHEN Miao－miao，LUO Juan，etal.An energy efficient nodes tracking algorithm in wireless sensor network[J].Journal of Hunan University：Natural Sciences.2009，36（1）：81－84.（In Chinese）

[3] 馮琳，段復建 .基于錐模型的非單調自適應信賴域算法[J].山西大學學報：自然科學版，2011，34（4）：580－586.FENG Lin，DUAN Fu－jian.A Non－monotone self－adaptive trust region method based on the conic model[J].Journal of Shanxi University：Natural Science Edition，2011，43（4）：580－586.（In Chinese）

[4] 何松華，程凡永，陳威兵，等.基于數據外推的限帶信號最大似然譜估計[J].湖南大學學報：自然科學版，2009，36（3）：85－88.HE Song－hua，CHENG Fan－yong，CHEN Wei－bing，etal.Band－limited signal spectrum estimation based on data extropolation and maximum likelihood criterion[J].Journal of Hunan University：Natural Sciences，2009，36（3）：85－88.（In Chinese）

[5] GERSHMAN A B，TURCHIN V I，ZVEREV V A.Experimental results of localization of moving underwater signal by adaptive beamforming [J].IEEE Trans Signal Processing，1995，43（10）：2249－2257.

[6] 周諱，唐南，于美華.一種快速的特征空間自適應波束形成算法[J].電子信息對抗技術，2009，24（4）：39－42.ZHOU Hu，TANG Nan，YU Mei－hua.A fast eigenspacebased adaptive beamforming algorithm[J].Electronic Information Against Technology，2009，24（4）：39－ 42.（In Chinese）

[7] HARRY LAND VAN TREES.最優陣列處理技術[M].湯俊譯 .北京：清華大學出版社，2008：382－392.HARRY LAND VAN TREES，TRANS.TANG Jun.Optimum array processing part IV of detection，estimation，and modulation theory[M].TANG Jun Translate.Beijing：Tsinghua University Press，2008：382－392.（In Chinese）

[8] CARLSON B D.Covariance matrix estimation errors and diagonal loading in adaptive arrays[J].IEEE Trans on Aerospace and Electronic Systems，1988，24（4）：397－401.

[9] VOROBYOV S A，GERSHMAN A B，LUO Z Q.Robust adaptive beamforming using worst－case performance optimization：a solution to the signal mismatch problem [J].IEEE Trans Signal Processing（S1053－587X），2003，51（2）：313－323.

[10] GUERCI J R.Theory and application of covariance matrix taper for robust adaptive beamforming[J].IEEE Trans on Signal Processing，1999，47（4）：977－985.

[11] 張賢達，保錚.通信信號處理[M].北京：國防工業出版社，2000：324－326.ZHANG Xian－da，BAO Zheng.Communication signal processing[M].Beijing：China National Defence Industry Press，2000：324－326.（In Chinese）