例談物理過程分析對解題的作用

趙 榮 詹春蘭

（鳳慶縣第一中學 云南 臨滄 675900）

隨著高考改革的深入，各地高考物理試卷都十分注重對物理過程的考查，這是由于物理過程能較好地反映和體現高考物理所需要考查的物理概念以及各種能力要素.考試說明中提出了對學生的理解、推理、分析綜合、應用數學處理物理問題、實驗等5種能力的明確要求，因而在物理教學中，提高學生思維素質，培養學生解決物理問題的能力是一個重要的目標.正確而準確地分析各種物理過程是培養學生5種能力特別是綜合分析能力的一個重要途徑.學生經常在解綜合問題時無從下手，找不到突破口，重要原因就是良好思維習慣培養不夠和思維素質還不夠高，分析能力還有欠缺，這樣大大降低了解題的準確程度.我們希望學生有一個良好的思維習慣和學習方法，故而強調對物理過程的分析.在這種分析、推理過程中研究物理變化的規律及各種物理量的變化，挖掘出潛在的解題條件，排除不必要的干擾因素，找出難度較大的臨界問題，從而迅速、準確地確立解題的策略和方法，同時在分析過程中也就使自己的思維素質得到了提高.

1 挖掘隱含條件

物理之所以難，不僅因為物理過程復雜多變，還由于潛在條件隱蔽難尋，使人感覺條件不足而陷入困境.物理狀態的變化過程有的簡單、有的復雜，有單一過程的延伸，又有不同物理過程的交叉.解題時，要冷靜分析、判斷各個階段的特點，找出它們之間的聯系，挖掘過程進行中隱含的條件.

【例1】在光滑的水平軌道上兩個半徑都是r的小球A和B，質量分別為m1和m2，當兩球心間距離大于L（比2r大得多）時，兩球之間無相互作用力；當兩球心間的距離等于或小于L時，兩球間存在相互作用的恒定斥力F，設A球從遠離B球處以速度v0沿兩球連心線向原來靜止的B球運動，如圖1所示，欲使兩球不發生接觸，問v0必須滿足什么條件？

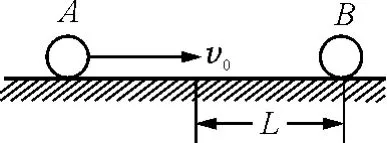
圖1

解析：A球向B球接近至A與B間距小于L后，在兩球接觸前，由于受斥力作用，A球開始做減速運動，速度逐步減小，B球在前做加速運動，速度由零增大，二者速度相等前，兩球間距逐步減小；當二者速度相等后，如還未接觸，A球繼續減速，B球繼續加速，兩球間距逐步增大，故當A，B速度相等時，兩球間距最小，若此距離大于2r，則兩球不會接觸.設兩球間距最小時A和B兩球的速度為v1和v2；兩球間距從L變至最小的過程中，A，B兩球發生的位移分別為s1和s2，則兩球不接觸的條件是

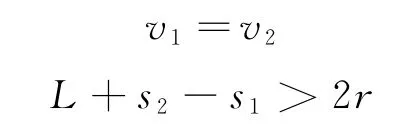
對兩球由動量守恒定律得

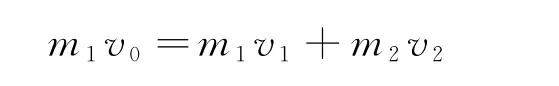
對兩球分別由動能定理得

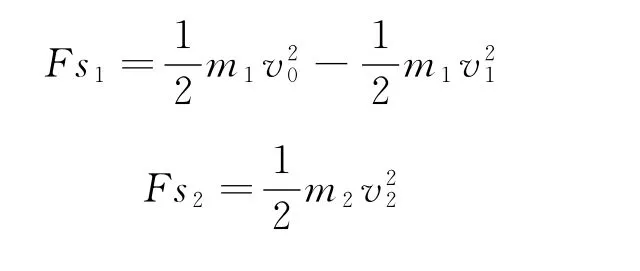
聯立以上幾式得

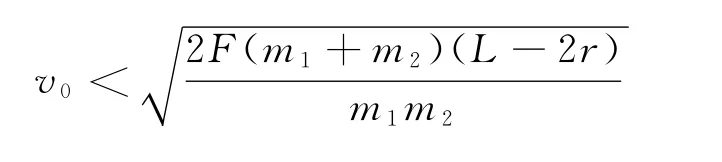
特殊的是當n＝1，即m1＝m2＝m時

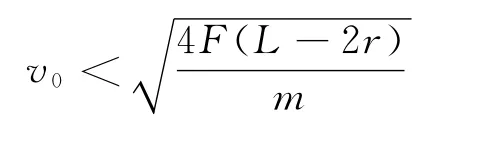
從物體運動過程分析中，可找到隱藏在物理過程中的解題的關鍵條件：當A和B速度相等時，兩球間距最小.

2 了解各物理量的變化

在一些靈活性較高的物理題中，物理量不是一成不變的，隨著物理過程的變化，一些物理量的大小、方向均可能發生變化，抓住這些變化的過程及轉變的時刻或位置往往成為解題的關鍵.

【例2】如圖2（a）所示，在磁感應強度為B的勻強磁場中，有一足夠長的絕緣細棒ON，與水平面夾角α，一質量M，帶電荷量為＋q的圓環A套在ON棒上，環與棒間的摩擦因數為μ，且μ＜tanα，現讓小環A由靜止開始下滑，試問：小環在下滑過程中

（1）小環A的最大加速度為多大？此時的即時速度多大？

（2）環A能達到的最大速度多大？

圖2

解析：在開始位置，環受重力、彈力、摩擦力作用，如圖2（b）.環啟動，有了速度，立即受到洛倫茲力的作用，與彈力同向.隨速度的增大，彈力逐漸減小，摩擦力逐漸減小，此階段作的是加速度逐漸增大的加速運動.當速度大到使洛倫茲力等于mgcosα時，摩擦力為零，加速度達最大，即am＝gsinα，如圖2（c）.

速度繼續增大，洛倫茲力大于G2，此瞬間彈力反向，摩擦力逐漸增大，此階段做的是加速度逐漸減小的加速運動，當速度大到使摩擦力等于G1時，加速度為零，速度達最大，如圖2（d）.

此過程的分析使學生清晰地看到了各物理量的變化情況：速度由零增大到最大值；加速度由小增大到最大再減小到零；彈力由大（mgcosα）減小到零，再增大到定值（mgcosα此時達穩定速度a＝0，v＝vm）；而洛倫茲力由零增大到某定值.分析清楚了各物理量的變化，使思維清晰而準確，解題也就順理成章了.

（1）當下滑初期Bqv＜mgcosα，壓力FN垂直棒向上，小球下滑加速度由

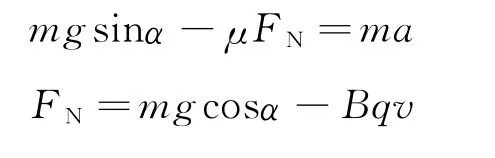
聯立得

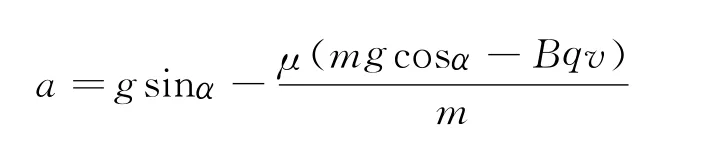
由此可知a隨v的增大而增大，小球做加速度增大的的加速運動，當Bqv0＝mgcosα時，此時

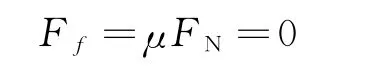
這時的臨界速度

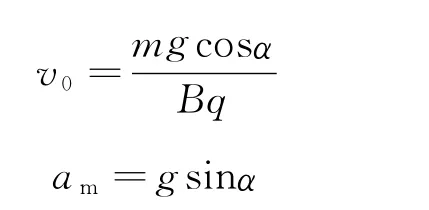
（2）當Bqv′＞mgcosα后，FN′垂直棒向下，小球下滑的加速度由

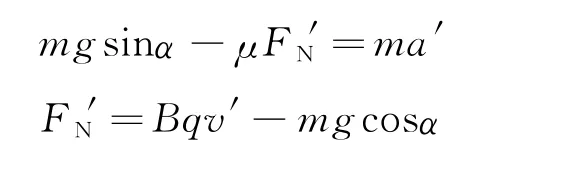
聯立得

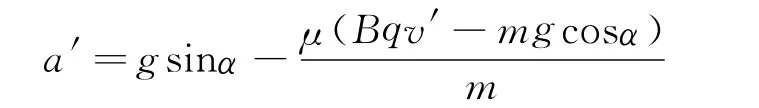
由此可知a′隨v′增大而減小，即可判斷小球將改做加速度減小的加速運動，當mgsinα＝μFN′時，a′＝0，此時速度最大，可得

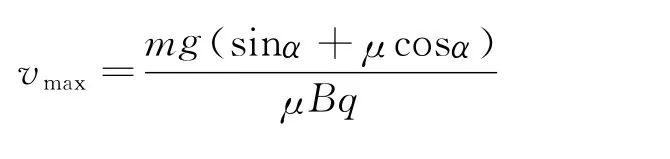
3 排除干擾因素

經常遇到一些物理題故意多給已知條件，或解題過程中精心設置一些歧途，或安排一些似是而非的判斷，也就是利用干擾因素考查考生明辨是非的能力.這些因素的迷惑程度愈大，愈容易在解題過程中犯錯誤.選擇題就是比較典型的迷惑題.因此，如何從分析物理過程中排除這些干擾因素，得出正確的結果是十分重要的.

【例3】以10m／s速度行駛的汽車，司機發現右前方54m處有一以4m／s的速度與汽車同方向勻速行駛的自行車，司機以－0.25m／s2的加速度開始剎車，問汽車停下前會不會和自行車相遇？若能相遇，相遇幾次？

錯解：設汽車從開始剎車至停下用時為t，則

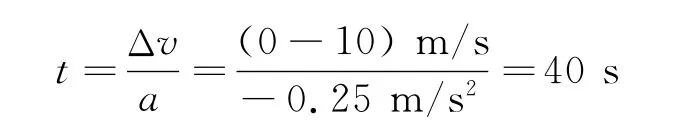
在40s內汽車前進的路程

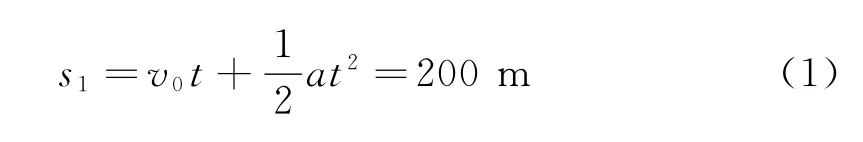
在40s內自行車前進的路程

而相遇的條件是

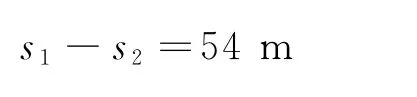
從（1）、（2）式得

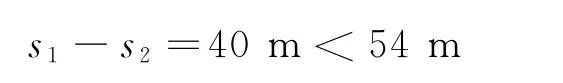
從中得出不相遇的錯誤結論.

解析：在認真分析汽車運動過程中不難發現，汽車速度減至4m／s前就已追上自行車相遇過一次，隨后汽車停下前，自行車可能追上汽車再次相遇.設相遇時間為t，由相遇的條件有代入數據解得：t1＝12s和t2＝36s，都小于汽車停下用時的40s，其意為12s時汽車從后追上與自行車相遇；36s時自行車從后追上與汽車相遇.故相遇兩次.

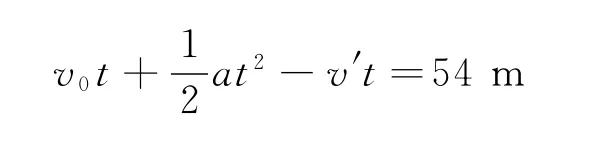
此題的干擾因素就是汽車從開始剎車至停下用時40s.如果不認真分析物理過程，不懂得不發生相遇的判斷條件是車速v＝4m／s前若不相遇，則不會相遇，而不是v＝0，就會出現錯解.

4 確定物理模型

法國科學方法論學者阿雷曾說過：“科學的基本活動就是探索和制定模型”.物理學研究的方法通常都要從“選模型”入手，物理模型是反映現象本質特征的物理圖景.物理學的研究對象都是經過一定程度抽象化或理想化的模型.利用抽象、理想化、簡化和類比等方法，把反映研究對象的本質特征抽象出來，構成一個概念或實物的體系，即形成物理模型.

在中學物理中物理模型可大致分為三大類：一是研究對象模型，如，質點、剛體、杠桿、斜面、彈簧振子、單擺、理想氣體、理想流體、點電荷、試驗電荷、理想導體、理想電表、純電阻、純電容、純電感、直線電流、環形電流、理想變壓器、光線、點光源、薄透鏡、原子模型；二是條件模型，如，絕熱物質、均勻介質、勻強電場、勻強磁場、輕桿、輕繩、光滑平面等；三是過程模型，如，勻速直線運動、勻速圓周運動、勻變速直線運動、平拋運動、簡諧振動、彈性碰撞、完全非彈性碰撞、反沖運動模型、等溫過程、等容過程、等壓過程、絕熱過程、恒定電流、磁場中導軌上的金屬棒的運動模型、汽車啟動模型、鏈式反應模型等.

在高中物理中建立了一系列的對象模型和過程模型，使在研究問題時能抓住主要因素，摒棄次要因素.因而解決物理問題時，往往從分析物理過程中確定所研究問題與熟知的那種模型相似，從而迅速找到解決問題的方法.

【例4】長為4L的粗細均勻的金屬桿圍成一個正方形閉合框架，框架放在光滑的水平桌面上，另一根長為L的同種材料、同樣粗細的金屬桿擱在其上，如圖3所示，勻強磁場垂直穿過整個框架平面，不計一切摩擦，當直桿ab獲得一個初速度沿框架從左向右運動的過程中

（1）達到穩定運動狀態前，任一時刻桿ab加速度大小與框架加速度大小的關系；

（2）如框架、磁場足夠大，ab質量為m，初速度為v0，則從ab獲得初速度開始到ab達到穩定運動狀態過程中整個電路產生的焦耳熱.

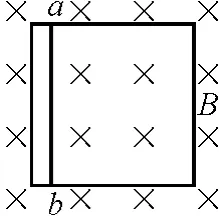
圖3

解析：ab桿運動切割磁感線產生感應電流立即受到相反方向的安培力作用，做加速度逐漸減小的減速運動，而框架卻受到方向與ab運動方向相同的安培力作用，做加速度逐漸減小的加速度運動.前者減速，后者加速，某瞬間時會具有共同速度，以后無感應電流，也就沒有了安培力作用，它們達到穩定運動狀態，一起以共同速度勻速運動.在相對運動過程中，由于棒和框架中流過的感應電流的大小同時刻總是相等而方向相反（切割磁感線邊），因此受到的安培力亦總是大小相等而方向相反，桿和框架所組成的系統所受合外力為零，因此這一過程正類似于學生熟知的“完全非彈性碰撞”模型，符合動量守恒定律條件，立即找到了解題方法.

（1）ab桿的初速為v0，質量為m，據題述框架質量為4m.達到穩定運動狀態前任一時刻桿ab加速度大小與框架加速度大小的關系為

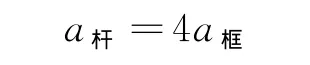
（2）對桿和框架組成的系統，由動量守恒定律有

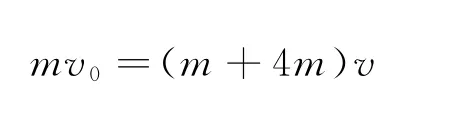
得

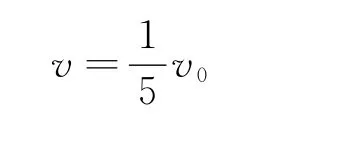
在相對運動過程中，一部分機械能轉化為感應電流的電能.這些電能克服電阻做功而轉化為內能，即為整個電路放出的熱量.根據能的轉換和守恒定律，棒和框架放出的熱量等于系統機械能的減少量，又與熟知的“完全非彈性碰撞”中動能的減少量相同，由此得出

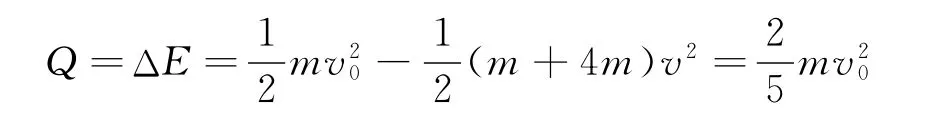
通過此題的分析可看出，抓住桿和框架合外力為零的條件，且最終具有共同速度，找到正確的物理模型，采用熟知的解題方法，使一個較綜合的物理問題迅速而準確地得到了解決.

5 找出臨界狀態和條件

物理過程千變萬化，抓住變化的關鍵時刻和位置，即分析處理好臨界條件是十分重要的.一般來說，在物理題中凡涉及臨界條件的問題都是較困難的，因而在研究物體的變化規律或發展趨勢時要考慮某些變量或改變因素對研究對象的影響，必須在分析物理過程時掌握“動態分析”方法去推求極值或臨界條件.

【例5】如圖4所示，一重為G的均勻球，放在光滑斜面上，斜面傾角為α，在斜面上有一光滑的不計厚度的木板擋住球，使之處于靜止狀態，今使擋板與斜面的夾角β緩慢增大至擋板接近水平，在此過程中球對斜面的壓力FN和球對擋板的壓力FN′的變化情況是

A.FN不變，FN′先減小后增大

B.FN不斷減小，FN′不斷減小

C.FN不變，FN′不斷增大

D.FN不斷減小，FN′先減小后增大

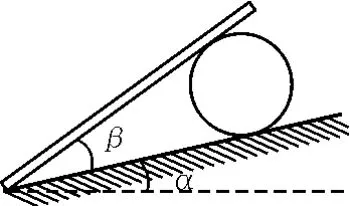
圖4

解析：擋板與斜面的夾角β緩慢增大至擋板接近水平過程中，小球緩慢沿斜面下降，故可視為運動過程中各點均處于“靜止”狀態，即該題為小球處于動態平衡過程，屬受共點力平衡問題.將小球受重力分解為FN和FN′，如圖5所示，斜面固定，則FN的方向不變，在擋板與斜面的夾角β緩慢增大至擋板接近水平，圖中對應FN1和FN1′，FN2和FN2′，FN3和FN3′，由圖看出，FN不斷減小，FN′先減小后增大，當擋板與斜面垂直時，FN′最小，故選D.

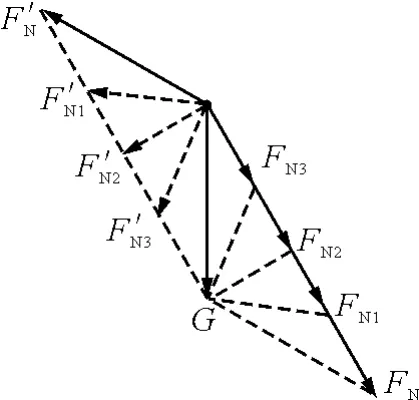
圖5

從此題的分析可看出，通過分析小球“動態型”平衡問題，從題設中尋找某些不變因素，化動為靜處理并得出當擋板與斜面垂直時，FN′最小的臨界極值特征.

又如例1中，當A和B速度相等，即兩球間距最小的時刻、例2中的彈力反向時刻、例3中速度為4 m／s的時刻、例4中桿和框架具有共同速度的瞬間，這些都是物理量發生變化的關鍵時刻，也是分析物理過程必須抓住的關鍵點，也是解題的關鍵.

從以上可以看出，通過對物理過程分析的訓練，能使學生思維的嚴密性、深刻性、靈活性、概括性、獨創性及邏輯推理能力得到發展和提高，因而養成分析物理過程的習慣是培養思維素質，提高解題能力的重要手段和途徑.

1 梁樹森.物理學習論.南寧：廣西教育出版社，1996.85～87

2 陳林橋.分析物理過程的幾種方法.物理教師，2008（6）：50～52

3 朱紅軍.物理解題思維方法點撥.試題與研究，2007（4）