非等間距GM(1，1)冪模型及其工程應用

王正新，黨耀國，劉思峰

(1.浙江財經學院經濟與國際貿易學院，杭州 310018;2.南京航空航天大學經濟與管理學院，南京 210016)

1 前言

近年來，灰色系統預測方法[1，2]被廣泛應用于非等間距序列的建模與預測，其應用范圍主要集中在建筑物變形[3，4]、材料實驗[5，6]、巖石力學[7]、資源勘探[8]等工程領域。由于灰建模不需要大量樣本數據就能建模預測，且建模過程簡單、易于操作，在小樣本序列的短期預測中具有獨特的優勢，經典灰色預測模型同樣具有較高的工程應用價值[9，10]。現有的非等間距灰色預測模型主要是經典GM(1，1)模型和灰色Verhulst模型的簡單推廣，模型改進主要集中在背景值的優化。鄧聚龍教授在分析非等間距序列的灰導數及其背景值的基礎上，提出了非等間距 GM(1，1)模型[11]。文獻[12] 利用文獻[13] 優化的背景值構建非等間距GM(1，1)模型，其建模精度高于直接建模法。文獻[14] 則將具有最優背景值[15]的 GM(1，1)模型拓展為非等間距模型，獲得了較高的預測精度。文獻[4] 則通過優化非等間距灰色Verhulst模型的背景值，改善傳統建模方法的模擬和預測精度。

GM(1，1)冪模型[1]是一種重要的非線性灰色模型，可以通過尋找與實際數據最匹配的冪指數，從而使得模型能夠較好地反映數據的非線性特征。但是自從鄧聚龍教授提出該模型以來，人們對它的關注甚少。筆者在文獻[16] 中首次提出了經典GM(1，1)冪模型的求解方法，研究了模型解的性質。目前，經典GM(1，1)冪模型還難以被應用到工程中大量存在的非等間距序列的建模中。文章將首先分析非等間距序列的生成方法，在此基礎上將經典GM(1，1)冪模型[16]拓展為非等間距 GM(1，1)冪模型，并研究模型中參數的優化問題。由于GM(1，1)模型和灰色Verhulst模型均是GM(1，1)冪模型的特殊形式。因此，只要能夠通過恰當的手段找到非等間距GM(1，1)冪模型的最優冪指數，其建模精度一定可以超越非等間距GM(1，1)模型和灰色Verhulst模型。

2 非等間距GM(1，1)冪模型

2.1 非等間距序列生成

序列生成是灰色系統建模的前提和基礎，筆者首先給出非等間距序列的灰色累加生成、累減還原及均值生成的定義。

1)定義1:設序列

X(0)(tk)= (x(0)(t1)，x(0)(t2)，…，x(0)(tn))，

若間距 Δtk=tk－ tk－1≠ const，k=2，3，…，n，則稱序列X(0)(tk)為非等間距序列。

2)定義2:設序列X(0)(tk)為非等間距序列，若，則稱序列

X(1)(tk)= (x(1)(t1)，x(1)(t2)，…，x(1)(tn))為非等間距序列X(0)(tk)的一階累加生成(1－AGO，1－accumulated generating operation)序列。

3)定義3:設序列X(1)(tk)如定義2所述，若x(0)(tk)則稱序列

X(0)(tk)= (x(0)(t1)，x(0)(t2)，…，x(0)(tn))為非等間距序列X(1)(tk)的一階累減還原(1－IAGO，1－inverse AGO)序列。

4)定義4:設序列X(1)(tk)為一階累加生成序列，若 z(1)(tk)=0.5(x(1)(tk)+x(1)(tk－1))，k=2，3，…，n 。則稱序列

Z(1)(tk)= (z(1)(t2)，z(1)(t3)，…，z(1)(tn))為非等間距序列X(1)(tk)的緊鄰均值生成序列。

2.2 非等間距GM(1，1)冪模型的建立

根據鄧聚龍教授關于灰導數[1] 的定義，可以得到非等間距序列的灰導數為:

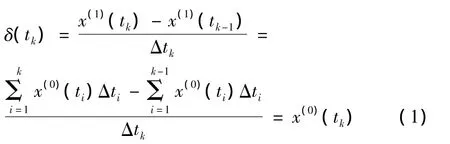
灰導數δ(tk)的白化背景值為X(1)(tk)的緊鄰均值生成序列Z(1)(tk)。

1)定義5:設 X(0)(tk)為非等間距序列，x(0)(tk)為灰導數，Z(1)(tk)為灰導數背景值，則稱

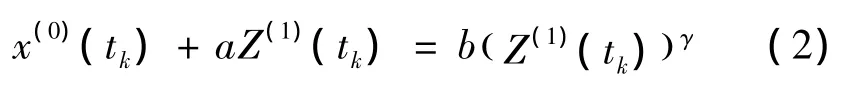
為非等間距GM(1，1)冪模型的灰色微分方程(為了更好地區別模型中的發展系數a，文章用γ表示文獻[16] 中的α)。

當γ=0時，式(2)為非等間距GM(1，1)模型;當γ=2時，式(2)則為非等間距灰色Verhulst模型。由此可見，只要處理好冪指數γ的選取問題，非等間距GM(1，1)冪模型完全可以覆蓋非等間距GM(1，1)模型和灰色Verhulst模型的應用范圍，并超越它們的預測精度。

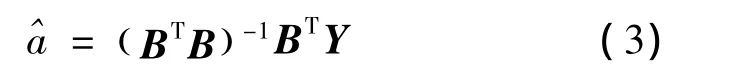
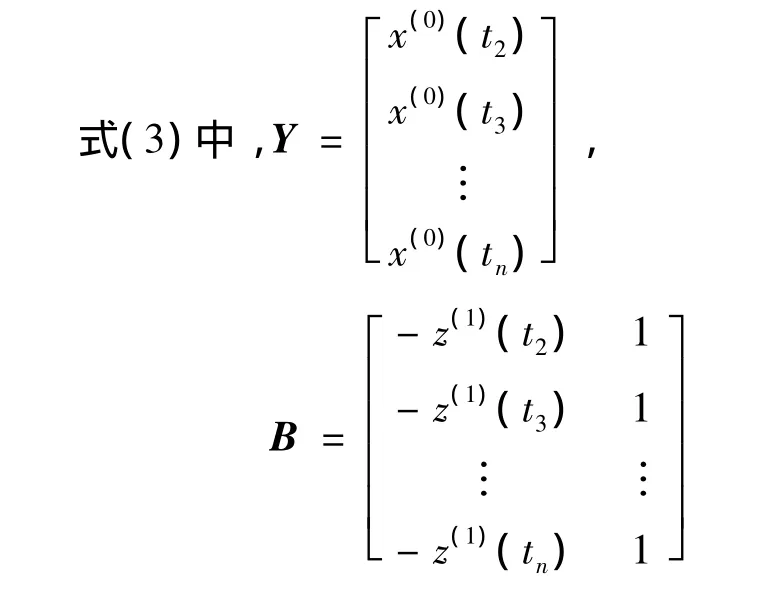
3)定義6:設X(0)為非等間距序列，X(1)(tk)為X(0)(tk)的1－AGO序列，=(a，b)T，則稱

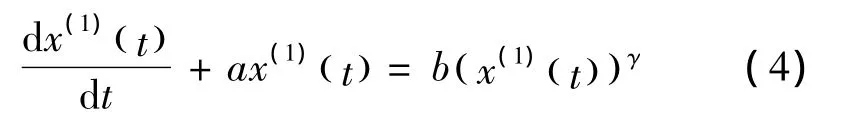
為非等間距GM(1，1)冪模型的白化方程。

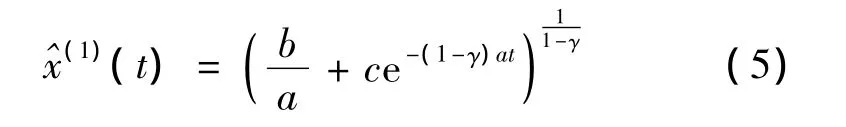
若以x(1)(tk)為初始值，非等間距GM(1，1)冪模型的時間響應序列為:

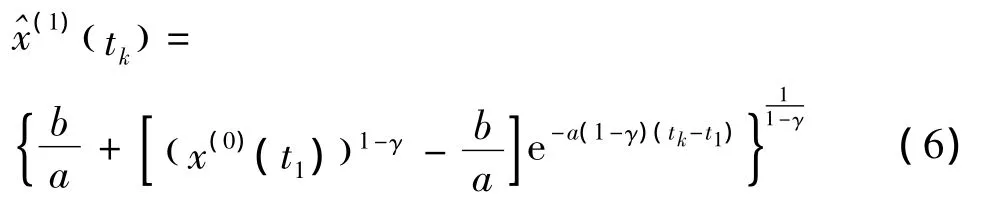
還原值為:

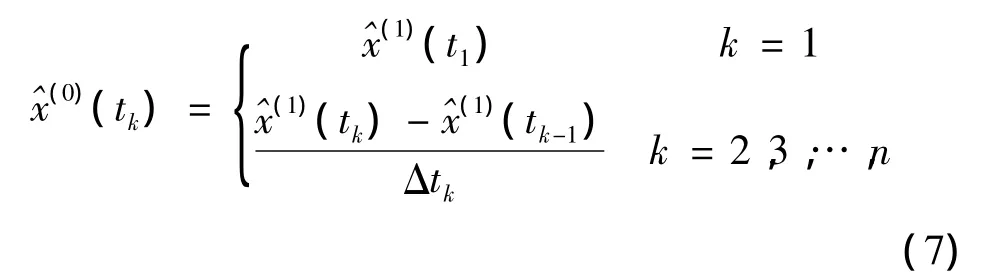
2.3 模型參數的確定

在實際應用中，可以利用非線性規劃的方法來求解冪指數γ。一旦γ確定，式(2)中的參數a和b也就確定了。首先將非等間距GM(1，1)冪模型中的參數a和b的代數表達式進行展開，經整理得:

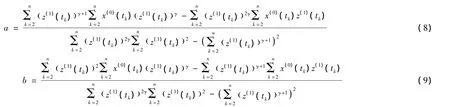
以平均相對誤差最小化為目標，以參數之間的關系為約束條件，可建立以下優化模型，以便求出最優的冪指數γ的值。

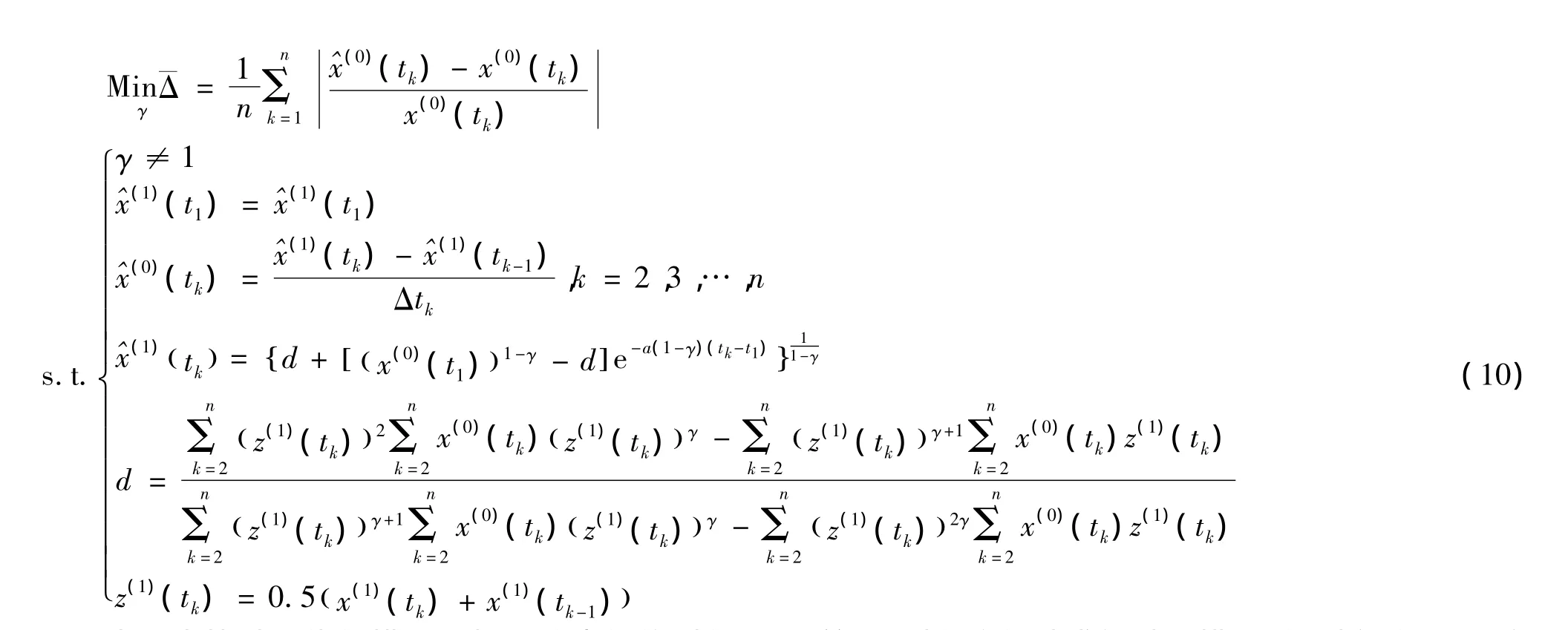
為了去掉以上優化模型目標函數中的絕對值，引入以下定理。

引理 1[17]:對于任意 n 個實數 f1，f2，…，fn，有:

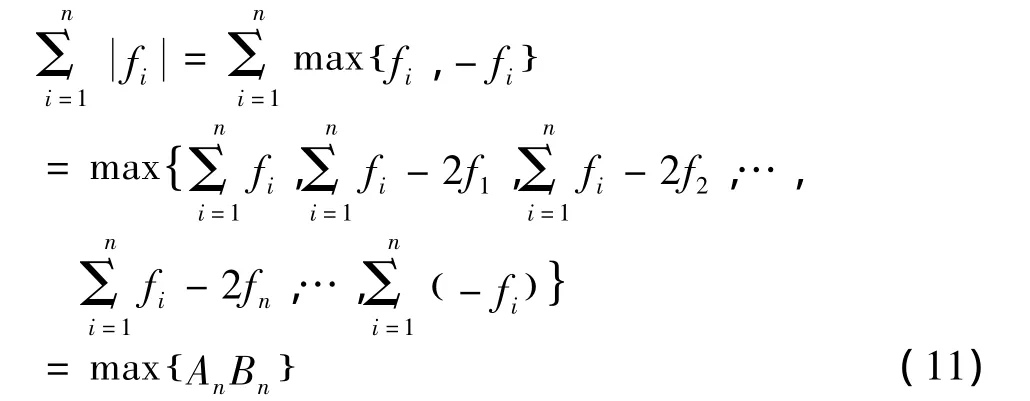
其中，An= (f1，f2，…，fn)，Bn為n×2n矩陣，Bn的每一列都是1或－1允許重復的排列。

因此，文章優化模型中的目標函數可以轉化為以下等價目標:

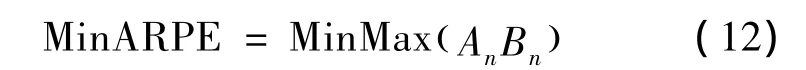
An，Bn的每一列都是1或－1允許重復的排列。

通過運籌學軟件 LINGO(或 MATLAB、EXCEL等)可以很方便地求解以上模型，得到參數γ、a和b的優化值。將以上方式獲得的參數值代入非等間距GM(1，1)冪模型求解過程，便可以獲得理論上誤差最小的模擬結果。

3 工程實例

P.G.福雷斯研究了溫度對鈦合金疲勞強度的影響，羅佑新從福雷斯所給實驗曲線中采集到鈦合金疲勞強度隨溫度變化的數據，如表1所示[5]。

表1 鈦合金疲勞強度隨溫度變化關系Table 1 The relationship between the fatigue strength of titanium alloy and temperature

為了便于計算，對原始數據作如下線性變換T=50+50tk，k=2，3，…，9;x(0)=(σ－1－400)/50，變換后的數據見表2。

表2 鈦合金疲勞強度隨溫度變化數據處理后的關系Table 2 The data processed relationship between the fatigue strength of titanium alloy and temperature

1)非等間距 GM(1，1)模型[5]。文獻[5] 建立的GM(1，1)模型時間響應式為:

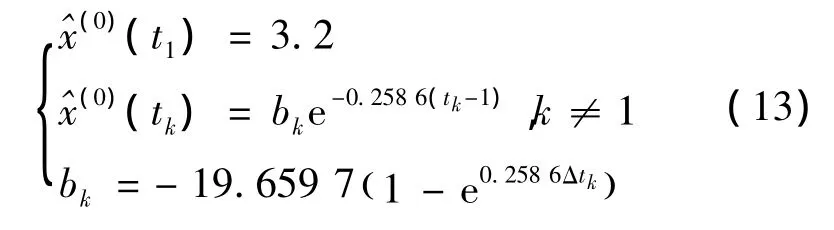
2)非等間距GM(1，1)冪模型。最優值γ=0.003593 ，a=0.25091 ，b=4.291305 ，可得時間響應式為:

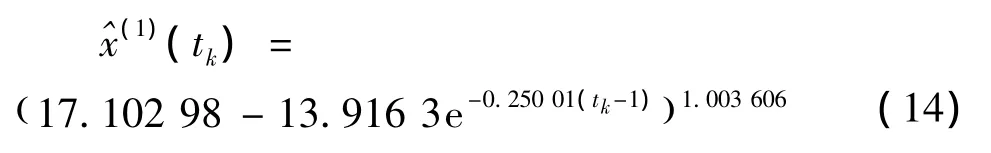
還原值為:

兩種模型的模擬值與實際值的比較見表3。

由表3可看到，文獻[5] 的方法和文章提出的非等間距GM(1，1)冪模型都取得了較高的建模精度，但是非等間距GM(1，1)冪模型的誤差顯著小于文獻[5] 的方法。除第一個時點外，文章方法在每個時點的模擬誤差都小于文獻[5] 的方法，總體來看，文章方法的平均誤差僅為0.94%，顯著小于文獻[5] 的2.77%。筆者認為，主要原因就在于非等間距GM(1，1)冪模型的形式較為靈活，可根據數據的特點調整模型的冪指數的大小。非等間距GM(1，1)模型直接取冪指數γ=0，而文章的優化結果顯示γ=0.003593更適合本例中的原始數據。

表3 兩種模型的模擬值與實際值的比較Table 3 Comparison of the modeling results of the two grey models

4 結語

當非等間距GM(1，1)冪模型中的冪指數取0和2時，分別等價于GM(1，1)模型和灰色Verhulst模型。非等間距GM(1，1)冪模型中的冪指數γ取值的多樣性賦予了該模型形式的靈活性的特點，只要通過合適的方法獲得最佳冪指數γ的值，則一定可以獲得理想的建模精度，其應用范圍已經覆蓋了非等間距GM(1，1)模型和灰色Verhulst模型。由此可見，非等間距GM(1，1)冪模型在工程中有著更為廣泛的應用前景。

[1] 鄧聚龍.灰理論基礎[M] .武漢:華中科技大學出版社，2002.

[2] Liu Sifeng，Lin Y.Grey Information Theory and Practical Applications[M] .London:Springer－ Verlag，2006.

[3] 齊長鑫，汪樹玉.灰色系統模型在壩基位移預測中的應用[J] .水利學報，1996(9):49－52.

[4] 偶昌寶，俞亞南，王戰國.不等時距灰色Verhulst模型及其在沉降預測中的應用[J] .江南大學學報(自然科學版)，2005，4(1):63－65.

[5] 羅佑新，周繼榮.非等間距GM(1，1)模型及其在疲勞試驗數據處理和疲勞試驗在線監測中的應用[J] .機械強度，1996，18(3):60－63.

[6] 郭麗萍，孫 偉，鄭克仁，等.非等時距GM(1，1)直接模型及其在材料試驗數據處理中的應用[J] .東南大學學報(自然科學版)，2004，34(6):833 －837.

[7] 陳有亮.非等距時序灰色預測方法及其在巖石力學與工程中的應用[J] .系統工程理論與實踐，2003，23(11):130－134.

[8] 田 敏.煤層氣資源量預測中的灰色系統理論研究[D] .北京:中國石油大學，2008.

[9] 陳子錦，王福亮，陸守香.灰色預測模型GM(1，1)的適用性分析及在火災風險預測中的應用[J] .中國工程科學，2007，9(5):91－98.

[10] 毛占利，朱 毅，楊伯忠，等.火災事故的灰色－馬爾可夫模型預測研究[J] .中國工程科學，2010，12(1):98－101.

[11] Deng J L.A novel GM(1，1)model for non － equigap series[J] .The Journal of Grey System，1997，9(2):111 －116.

[12] 戴文戰，李俊峰.非等間距GM(1，1)模型建模研究[J] .系統工程理論與實踐，2005，25(9):89 －93.

[13] 羅 黨，劉思峰，黨耀國.灰色模型GM(1，1)優化[J] .中國工程科學，2003，5(8):50 －53.

[14] 王葉梅，黨耀國，王正新.非等間距GM(1，1)模型背景值的優化[J] .中國管理科學，2008，16(4):159－161.

[15] 王正新，黨耀國，劉思峰.基于離散指數函數優化的GM(1，1)模型[J] .系統工程理論與實踐，2008，28(2):61 －67.

[16] 王正新，黨耀國，劉思峰，等.GM(1，1)冪模型求解方法及其解的性質[J] .系統工程與電子技術，2009，31(10):2380－2383.

[17] 王義鬧，吳利豐.基于平均相對誤差絕對值最小的GM(1，1)建模[J] .華中科技大學學報(自然科學版)，2009，37(10):29－31.