大型電力變壓器內繞組徑向屈曲分析
吳明君,劉文里,李陽陽
(哈爾濱理工大學,黑龍江哈爾濱150080)
0 引言
通常在變壓器繞組外部發生短路時,短路電流和漏磁場相互作用下將產生軸向電動力和輻向電動力,軸向電動力將導致繞組沿軸向上發生相對位移,輻向電動力會使繞組發生失穩變形。由于變壓器內繞組輻向失穩是造成變壓器損壞一個主要原因。因此,為了研究大型電力變壓器繞組輻向電動力,本文將變壓器繞組簡化為力學模型,并對其分別建立3種單跨模型和1種有彈支的多跨模型,進行對比分析和應力計算,以采取相應措施,提高電力變壓器抗短路能力。
1 單跨度模型的分析
1.1 特征值失穩理論
本文采用特征值屈曲分析法[1],雖然線性屈曲分析只能確定結構屈曲載荷的上限,但對分析大型變壓器內繞組的變形非常適用。
線性屈曲分析以特征值問題為基礎,首先要求解線彈性加載狀態P0的載荷位移關系,即給定P0的解,其表達式為

式中:Ke為彈性剛度矩陣;U0為P0加載時所對應的位移。
假設前屈曲位移很小,可給出任意狀態(P、U和σ)的增量平衡方程為

式中Kσ(σ)為應力狀態下計算出的初始應力矩陣。
假設前屈曲特征是載荷P0的線性函數為

式中λ為比例因子或載荷因子。
于是,有

因此,在前屈曲范圍表達的增量平衡方程為
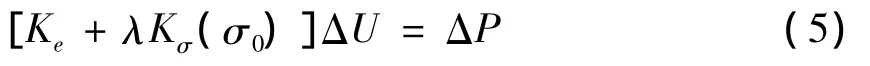
在臨界狀態時,結構在{ΔP}≈0時變形{ΔU}有所變化,因此方程可寫為

為滿足式(6),需滿足

計算最小特征值及其臨界載荷Pcr=λcrP0特征矢量,即為其屈曲形狀。
1.2 單跨模型的建立
取變壓器內繞組徑向兩支撐之間的線圈作為研究對象,以1臺220 kV/180 MVA三繞組變壓器為例進行分析,變壓器主要參數及低壓繞組主要參數如表1、表2所示,圖1為3種假設模型:圖1a為假定撐條處不發生相對位移及相對轉動,即固定支撐形式;圖1b為假定導線與撐條的連接處存在相對轉動,即假定為鉸接形式;圖1c是假定變壓器撐條為彈性支撐,用彈簧模擬其彈性支撐,并在連接處存在相對轉動。

表1 變壓器主要參數

表2 低壓繞組主要參數
1.3 3種模型的對比分析結果
模型中的約束均為圓柱坐標系[2],本文中的變壓器平均視在壓縮力為0.3 kN/cm。將上述3個模型分別進行臨界載荷的特征值屈曲分析,結果如表3所示。由表3分析可知,模型圖1 a中臨界載荷值很大,安全系數為49,與實際情況不符,其原因是固定端的約束條件。在實際運行中,在一定的范圍內提高軸向預緊力確實可以增大其臨界失穩值,但持續提高軸向預緊力對臨界失穩值的提高沒有顯著的效果。圖1b中導線與軸向支撐處有相對轉動,其臨界載荷值安全系數為13,若用此模型校核變壓器內繞組的幅向穩定性是比較危險的,因此將繞組的支撐改為彈性支撐圖1c,其臨界載荷值安全系數為5。

圖1 兩撐條間的3種支撐情況

表3 3種模型的結果分析
假設彈簧固定在剛性的圓筒壁上,因此彈簧的底部為全約束條件。彈性支撐的彈性系數若按靜態計算可根據力學特性計算求出,同時在靜態計算結果的基礎上還要考慮實際運行過程中存在撐條和繞組的摩擦系數以及外繞組在變形中對內繞組傳遞力系數的影響,因此,在模擬時對彈簧的彈性系數進行分析,結果如表4所示。繪出彈性系數K與安全系數的曲線,如圖2所示。
由表4分析結果可知,本臺變壓器若按此方法校核,彈性系數若低于0.3×108N/m,則在承受變壓器短路電磁力時將處于十分危險的狀況。由圖2分析可知,隨著支撐彈性系數的升高,其安全系數將逐步增加,當彈性系數趨近無窮時,即為剛性支撐,此時則與圖1b模型相近。從位移上可看出,隨著彈性系數的增加,位移量反而減小(這里僅研究沿徑向的位移,而不考慮總體壓力下的總體形變量)。因此,有彈支的模型圖1c最貼近實際運行情況,即便使用此種模型校核,其安全系數仍舊較高,但較前兩種理想模型而言已有較大的改進。若采用前兩種模型進行變壓器內繞組屈曲變形的校核是十分危險的。

表4 不同彈性系數下的數值分析

圖2 安全系數與彈性系數的關系
2 多跨模型的分析
2.1 模型的建立和臨界屈曲
考慮沿繞組圓周方向各種初始不均勻狀態對繞組幅向穩定性的影響,本文建立的多跨度彈支模型如圖3所示,假設繞組不能沿軸向運動,其余按實際情況約束分析,屈曲圖形如圖4所示。

圖3 多跨模型
2.2 模型結果分析

圖4 多跨模型的屈曲圖
由圖4分析可知,其屈曲臨界載荷為43.026 kN,平均視在臨界載荷為0.548 kN/cm。當撐條的彈性系數為1.0×108N/m時,安全系數為1.83,在其它條件相同的狀況下比兩端彈性支撐的模型所計算出的臨界屈曲載荷值更可靠,其原因是因為多跨度模型考慮了彈性支撐處節點之間位移、轉角的連續性和繞組內力相互傳遞的影響。
2.3 初始缺陷的情況
2.3.1 微扁圓形的初始缺陷
由于在變壓器裝配過程中存在一些誤差,繞組可能存在一些初始幾何缺陷[3]。一種較為常見的初始缺陷為繞組在裝配中出現的微扁圓情況,如圖5所示。在模型中將撐條的彈性系數從1.0×108N/m依次降低到0.65×108N/m,線圈與撐條的緊壓度越差,假定的彈簧彈性系數越低,其臨界屈曲圖形如圖6所示。由圖6分析可知,一階屈曲載荷為35.479 kN,平均視在臨界載荷為0.453 kN/cm,安全系數為1.51,比整個繞組導線全部緊貼在撐條時的安全系數降低了0.32個百分點。這說明存在幾何初始缺陷時繞組的臨界屈曲載荷值會降低,導致線圈在較低的電動力下發生失穩。在彈性系數不同時,在最小彈性系數附近,繞組最先發生屈曲變形。因此,在裝配過程中盡量保證繞組與撐條之間的緊密結合度和相對位移,對提高繞組在短路電磁力下的臨界載荷極其重要。
圖5 存在初始缺陷的示意圖
2.3.2 相鄰匝間空隙的初始缺陷

圖6 有初始缺陷的屈曲圖
由于變壓器繞組由N根導線并聯繞制而成,因此在輻向每相鄰導線之間存在匝絕緣和匝間空隙。一般認為相鄰匝之間導線完全緊靠,但實際繞組過程中因繞制方式、預緊力大小等因素導致導線之間完全緊靠沒有空隙。本文實例中變壓器的低壓繞組是12根導線并聯,因此分為3種模型進行分析,如圖7所示。圖7a中假設低壓繞組的線匝輻向上存在1處間隙,將12根導線分為兩部分(即內、外各6根導線),繞制方式按臥繞,則其繞組輻向裕度為1.03,空隙尺寸為1.2 cm;圖7b中假設繞組輻向上存在2處間隙,將12根導線分為3組(即內、中、外各4根),空隙為0.6 cm;圖7c中假設繞組輻向上存在3處間隙,將12根導線分為4組(每組3根),空隙為0.4 cm。

圖7 繞組存在初始缺陷的示意圖
在彈性系數及其它條件不變的情況下,圖7a中得到的臨界載荷為33.87 kN,安全系數為1.48;圖7b中得到的臨界載荷為32.95 kN,安全系數為1.44;圖7c中得到的臨界載荷為31.69 kN,安全系數為1.39。可見繞組的導線之間存在的空隙越多,在承受短路電磁力時的抗彎曲能力越差,在較小的短路電磁力下就會達到臨界載荷,使安全系數有所降低,不發生屈曲變形也會產生累積變形,使圓周方向上的預緊力分布更加的不均勻,對大型電力變壓器抗短路能力是十分不利的。因此,使用先進的繞制方式提高其安全裕度是十分重要的,許多廠家已經采取了相應的措施,如將臥式繞制方式改進為立式繞制方式,輻向計算裕度可提高至1.01,這樣可減少導線與導線之間的空隙,提高了電力變壓器繞組抗短路電磁力的能力。
3 結論
通過上述采取的3種單跨模型和1種有彈支的多跨模型,對大型電力變壓器內繞組徑向屈曲的分析與計算,得出以下結論。
1)大型電力變壓器的幅向失穩情況需要建立多種模型進行分析對比,才能獲取提高電力變壓器安全裕度和抗短路能力的繞組方式。
2)多跨彈支模型比其它模型能更好地分析變壓器徑向屈曲臨界載荷值,模擬存在初始缺陷時變壓器的屈曲情況,
[1]楊永謙,肖金生.實用有限元分析技術[M].北京:機械工業出版社,2010:106-107.
[2]尚曉江,邱峰,趙海峰.ANSYS結構有限元高級分析方法和范例應用[M].北京:中國水利水電出版社,2008:314-329.
[3]王曉鶯,王建民.變壓器故障與監測[M].北京:機械工業出版社,2010:145 -160.

