基于有限元的微型機器人足部仿真分析
蔡立斌
CAI Li-bin
(九江學院 信息技術中心,九江 332005)
0 引言
機器人是一種具有與人或生物類似的智能能力的自動化機器,兼具高度的靈活性。隨著現代科學技術飛速發展,微型機器人技術作為一種多學科交叉的高科技前沿技術也取得了長足發展,并在工業生產、日常生活活動中得到廣泛應用,如微型制造,醫藥以及血管的修復、治療等方面,其控制精度可以達到幾微米左右[1]。
有限元技術是由應用數值分析技術迅速發展而來的一項數值計算技術,在大多數工程應用及設計研究領域得到了廣泛的應用,它是一種結合數值分析技術與計算機技術交叉高度綜合的科學技術[2]。目前,我國的微型機器人設計與研究已向產業化方向發展,如果要實現中國機器人研發的產業化,就必須在從機器人關鍵零部件單元、機器人本體的優化設計以及總體性能設計等方面入手,開展相關的研發工作。而數值仿真技術的飛速發展,不僅縮短了機器人的研發周期,降低了研發成本,而且推動了機器人技術向高精尖的精密控制領域的發展[3]。
1 材料及仿真模型的建立
本微型機器人足部行走的方式與傳統機器人的足部有很大差異,它是足部導通電流產生熱引起足部變形而行走的。
本文根據微型機器人足部的工作原理,建立了硅質微機器人足部三維模型。圖1表示的是硅質微型機器人足部的縱向截面示意圖。微型機器人采用基于聚酰亞胺V型槽關節使微型機器人各條腿協調配合,從而進行自由運動的。用于制造V型槽關節的聚酰亞胺材料具有較高的熱膨脹系數,因此當V型槽關節通電流運動時,聚酰胺受熱,因此腿部會發生輕微彎曲。通過在微型機器人每條腿設置幾個V型槽,就可以獲得足夠的偏轉和彎曲撓度,從而實現機器人的運動(如圖1所示)。該微型機器人足部仿真分析所用到的材料:制備加熱電阻的聚甲基苯基硅氧烷,機器人足部的硅和氮化硅,制備復合層的氧化硅和鋁,固化聚酰胺。

圖1 硅質微型機器人足部的縱向截面示意圖
該有限元模型是一個瞬態傳熱電分析與準穩態熱機械分析相結合的模型,因此該有限元分析是一個電-熱-結構耦合分析,采用COMSOL Multiphysics的電流模塊、傳熱模塊和結構力學模塊來構建該微型機器人足部有限元分析模型。
為便于準確計算和分析,該模型進行了如下處理和假設:
1) 為便于模型建立,將熱傳導邊界條件等效為對流邊界條件。建模時的初始二維模型由超薄層構成的,為了減少在三維模型的網數量,對這些薄層進行必要的刪除操作是很有必要的。
2) 傳熱模型采用瞬態熱傳導對流進行求解,結構模型則采用準穩態固體力學進行求解,為解決電-熱-結構的問題,在力學模型中采用批處理策略和參數掃描法,將時間t設為掃描參數,這樣既解決了求解的穩定性問題,又解決了熱結構耦合的難題。
3) 很多數值模型都是采用單向熱電耦合——電流影響產熱,這種方法雖然增加了求解的收斂性,但無法反映溫度等對電阻產生的影響。因此,本文熱電模型采用熱電雙向耦合處理。
此模型涉及電-熱-結構多場耦合的問題,因此該分析包括三部分:1)涉及微機器人足部電流模型分析;2)涉及電流產熱及機器人熱傳導-對流傳熱模型分析;3)涉及微機器人足部受熱變形的結構模型分析。
1.1 電流模型
微型機器人啟動后,電流流過加熱電阻時,根據歐姆定律會產生一定量的電阻熱,這部分熱量就作為該模型的熱源。其電流PDE控制方程為,

其中s為電導率,V為電勢,Je為為外部電流密度,Q為電流源。
其中電導率s是電阻率R的倒數:

其中R0為參考電阻率,T0為參考溫度。
1.2 傳熱模型
此微型機器人模型中,采用基于固體傳熱的三維瞬態傳熱控制方程。其控制方程包括熱傳導和對流項:

其中k,r,C是材料的熱傳導系數、密度和比熱,它們都是溫度的函數;Q和v分別是熱源強度(即電流模型中電流的總功率損耗密度)和運動速度。
傳熱模型的另一個重要部分是在機器人模型對流冷卻邊界的建模。實驗證實,機器人通過加熱電阻產生的大部分熱量是從硅結構表明也就是在機器人的“身體”與周圍環境發生對流而釋放熱量的。此外,足尖端與地面之間是熱傳導邊界,為了簡化建模,將熱傳導邊界條件等效為對流邊界條件,其對流冷卻控制方程描述如下,

其中Text是周圍環境的溫度。采用較高的熱傳導性邊界作為鋁復合層傳熱邊界。用剛性彈簧條件來描述電阻層,其控制方程如下,

其中d為復合層厚度。此模型除與地面接觸的足尖端部分采用對流系數為1×104W/(m2·K)外,該機器人模型其余部位采用對流系數為1×105W/(m2·K)。在這里,對流系數的取值是隨意選擇的,但可以通過比較模擬結果與實驗數據來重新校正熱傳導系數。
1.3 力學模型
此微型機器人力學模型是基于COMSOL中的固體力學模型和線彈性材料模型建立的。其力學模型的控制方程為:
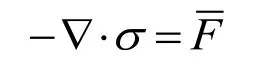
力學部分的邊界條件:約束機器人足底部左側的位移,而機器人結構的其余部分受力為零。三維模型中不包括Al和 SiO復合薄層。對由此產生的邊界,通過一個結構殼和兩個特定的熱邊界條件來模擬高熱傳導層和低熱傳導層。熱量傳輸通過機器人足部傳導時,由于幾種材料的熱膨脹系數的不同而導致足部出現彎曲行為。在剛性彈簧邊界條件下模擬的邊界溫度是間斷的,因此需要建立兩個傳熱模型。結構分析部分采用一個熱膨脹殼單元來模擬兩個薄層。COMSOL軟件會自動處理熱膨脹外殼和固體單元之間的耦合。
2 結果與討論
本模擬中,在兩個電阻上都施加30mV的電勢持續時間0.1ms,通過電流模型中電流的總功率損耗密度計算可知,由電阻熱產生的熱量源約為2·1013W/m3,相當于100 mW的熱量輸入。
結構力學部分的時間尺度與傳熱部分相比要小得多,所以可忽略結構分析中的質量效應。使用參數掃描分析將瞬態結構分析轉換為準穩態結構分析。這種方法把固體分析和傳熱分析結合起來,通過順序求解方式來進行模型的求解:首先求解傳熱和導電介質DC偏微分方程,然后,將計算結果存儲在指定文件中,設置指向存儲的計算機結構的線性化路徑,用時間變量參數t作為掃描參數來求解結構力學偏微分方程。圖4 所示在t=0.1ms和t =0.2ms時微型機器人足部的溫度場分布,從圖中可以看出t=0.1ms時,機器人足部最高溫度出現在加熱電阻處,t=0.2ms時,由于聚酰胺良好的導熱性,熱量傳遞到V型槽,因此這時最高溫度出現在V型槽。

圖2 在t=0.1ms和t=0.2ms時微型機器人足部的溫度場分布
圖3所示分別在t=0.1ms和t=0.2ms時微型機器人足部的變形(圖中黑色框圖表示未變形前的位姿,彩色框圖表示變形后的位姿),從圖3中可以明顯看出微型機器人的發生彎曲變形等現象,同時,正如預期的那樣足部的彎曲位移隨著溫度的增加而增大,當關閉電源(熱源)時機器人足部彎曲復原。圖4所示為微型機器人足部總位移隨時間的變化曲線,位移變化曲線的仿真和實驗結果的變化規律一致,在0.1ms彎曲撓度達到最大,在0.1ms后由于關閉電源(熱源)使其溫度迅速降低,導致機器人足部彎曲撓度也變小。
3 結論

圖3 在t=0.1ms和t=0.2ms時微型機器人足部的變形
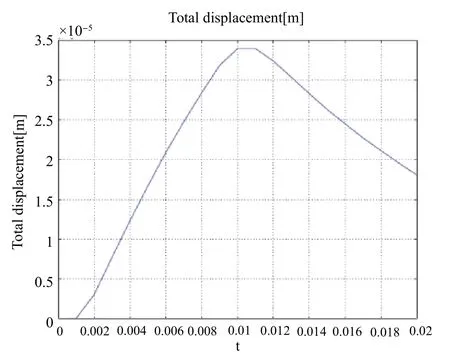
圖4 足尖的總位移 (隨時間變化)
本文在分析了微型機器人足部工作原理的基礎上,基于多物理場耦合原理,利用COMSOL多物理場耦合分析軟件建立了微型機器人足部三維電-熱-結構耦合模型,模擬并分析了硅質微型機器人運動過程中足部的溫度場以及彎曲變形行為。微型機器人足部彎曲變形等行為的模擬仿真結果與實驗結果取得了很好的一致性,因此該有限元模型是可以準確預測微型機器人足部的彎曲變形等行為。
[1]柴婷婷, 丁言露. 機器人仿真及其自動化研究進展[J]. 制造業自動化, 2011, 33(5): 87-89.
[2]俞志偉, 楊屹巍, 宮俊, 戴振東. 基于LPC2103的仿壁虎機器人控制系統設計[J]. 制造業自動化, 2011, 33(11):6-10.
[3]肖智勇, 段建中, 杜鑫強, 李建. Motoma工業機器人有限元靜態分析及改進設計[J]. 長沙理工大學學報, 2011,8(4): 71-76.

