利用過程性變式 創(chuàng)設(shè)探究性課堂

●童桂恒 (金華四中教育集團婺城中學(xué) 浙江金華 321025)

所謂“過程性變式”是指數(shù)學(xué)活動的有層次推進.這種層次性既可以表現(xiàn)為一系列的臺階，也可以表現(xiàn)為某種活動策略或經(jīng)驗.在數(shù)學(xué)活動過程中，教師通過對數(shù)學(xué)學(xué)習(xí)對象動態(tài)的、內(nèi)在的、有層次性的遞進，讓學(xué)生分步解決問題，并在解決問題的過程中積累多種活動經(jīng)驗.

1 利用過程性變式，改進定理教學(xué)模式

在數(shù)學(xué)教學(xué)中，學(xué)生要學(xué)習(xí)大量的性質(zhì)定理、判定定理和公式等，以往的數(shù)學(xué)學(xué)習(xí)常常是教師“告訴”定理公式，給出證明，然后通過練習(xí)做機械訓(xùn)練.學(xué)生對這樣的教學(xué)模式感到枯燥乏味，學(xué)習(xí)興趣陡降.因此，在定理教學(xué)中利用過程性變式，創(chuàng)設(shè)探究性的學(xué)習(xí)環(huán)境，讓學(xué)生在數(shù)學(xué)活動中增添數(shù)學(xué)學(xué)習(xí)的興趣，在變式訓(xùn)練中提高數(shù)學(xué)學(xué)習(xí)水平.

1.1 用情境問題引發(fā)興趣

案例1 “等腰三角形的判定”課堂教學(xué)設(shè)計

例1 如圖1，如何復(fù)原一個被墨跡浸漬的只剩一個底角和一條底邊的等腰三角形?

學(xué)生的3種方法分別是：

方法1：量出∠C度數(shù)，畫出∠B=∠C，∠B與∠C的邊相交得到頂點A.

方法2：作BC邊上的中垂線，與∠C的一邊相交得到頂點A.

方法3：對折.

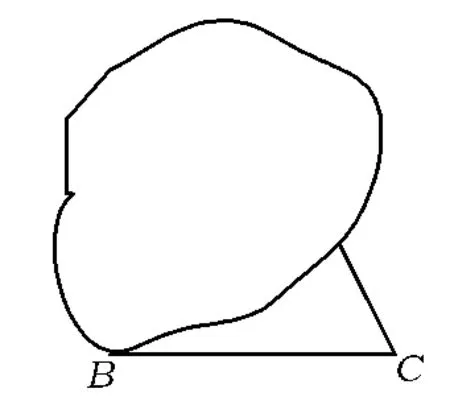
圖1

評注“數(shù)學(xué)知識需要形式化的表述，而教師的責(zé)任是返璞歸真，運用適度的非形式化方法，將數(shù)學(xué)的學(xué)術(shù)形態(tài)轉(zhuǎn)化為教育形態(tài)，展現(xiàn)數(shù)學(xué)的魅力，激起學(xué)生學(xué)習(xí)數(shù)學(xué)的熱情”.幾何源于現(xiàn)實生活，對于初學(xué)平面幾何的學(xué)生來說，選擇適當(dāng)?shù)臅r機，讓他們從個體實踐檢驗中學(xué)習(xí)，可以提高學(xué)習(xí)的主動性.在這里，第1種方法正好可以得出本節(jié)課要學(xué)的判定定理，第2種方法則是今后線段垂直平分線性質(zhì)的事實基礎(chǔ)，第3種方法則是等腰三角形對稱性的體現(xiàn).在探究的活動過程中，等腰三角形的判定定理不是由教師給出，而是讓學(xué)生憑借經(jīng)驗畫圖，那么畫出的圖形是不是等腰三角形呢?產(chǎn)生了問題，然后從問題出發(fā)，得出判定定理.這樣做，改變了學(xué)生被動接受的狀況，從而提高了學(xué)生的學(xué)習(xí)興趣和學(xué)習(xí)熱情.

1.2 多種證法激活創(chuàng)造力

例1的3種常規(guī)的證法如下：

(1)如圖2，作∠A的平分線，利用“角角邊”證明;

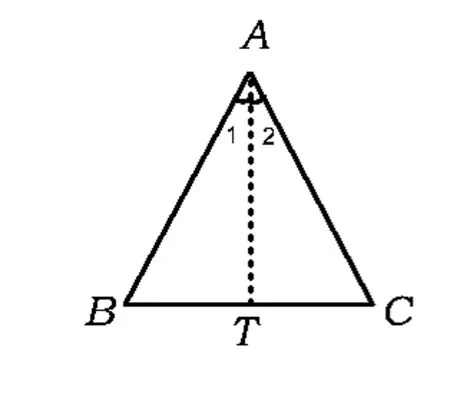
圖2

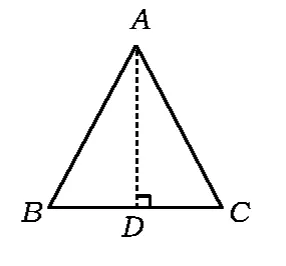
圖3

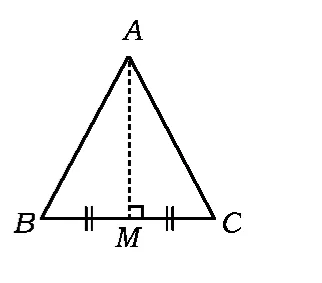
圖4

(2)如圖3，過點A作邊BC的垂線，利用“角角邊”證明;

(3)如圖4，作邊BC上的中線，“邊邊角”，不能證明.

例1的2種創(chuàng)造性的證法如下：

(1)如圖5，假定AB＞AC，由“大邊對大角”得出矛盾;

(2)如圖6，△ABC≌△ACB，應(yīng)用“角邊角”進行證明.

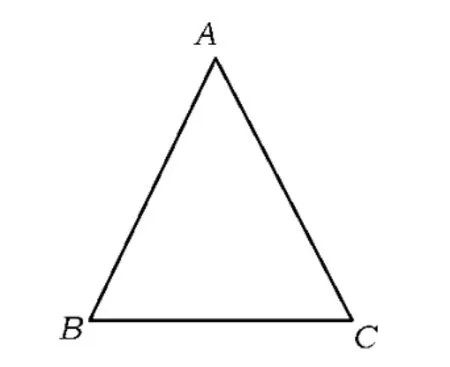
圖6

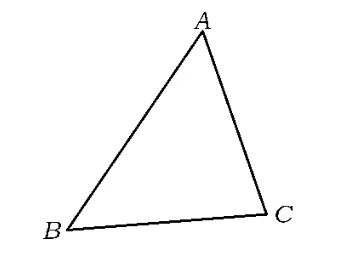
圖5

評注由于這節(jié)課利用學(xué)生的畫圖經(jīng)驗導(dǎo)出等腰三角形的判定定理，學(xué)生感到親切、自然，論證興趣很濃.第2種常規(guī)證法雖然是錯誤的，但學(xué)生在證明的過程中能發(fā)現(xiàn)問題，這種錯誤的嘗試可使學(xué)生吸取教訓(xùn)，積累經(jīng)驗，增長解題的能力，以后解決問題時可以少走“彎路”，避免盲目嘗試.2種不添輔助線的創(chuàng)造性證法，說明學(xué)習(xí)興趣的力量是不可低估的，學(xué)生學(xué)習(xí)的潛能是無限的.

1.3 用變式練習(xí)分步解決問題

通過不斷變換題目的條件，使不同數(shù)學(xué)學(xué)習(xí)水平的學(xué)生在數(shù)學(xué)活動中得到不同的發(fā)展.

(1)如圖 7所示，在△ABC中，∠ABC=∠ACB，BO平分∠B，CO平分∠C.能得出什么結(jié)論?

(2)若過點O作直線EF∥BC.圖8中有幾個等腰三角形?為什么?線段EF與線段BE，F(xiàn)C之間有何關(guān)系(學(xué)生編題)?

(3)若∠B與∠C不相等.圖9中有沒有等腰三角形?為什么?線段EF與線段BE，F(xiàn)C之間還有沒有關(guān)系(學(xué)生討論)?

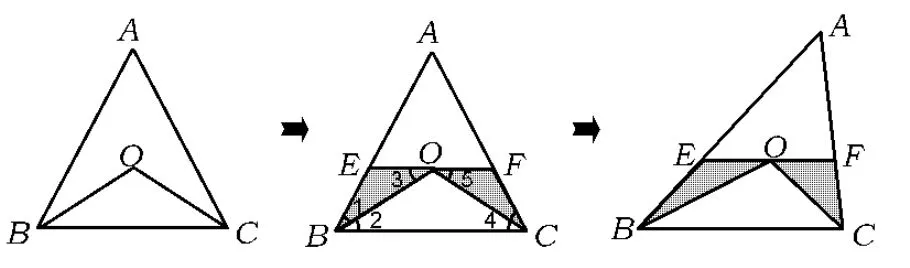
圖7圖8圖9

評注數(shù)學(xué)知識本身是一個多層次的結(jié)構(gòu)系統(tǒng).上述變式練習(xí)實際上經(jīng)歷了3步：在圖7中，學(xué)生直觀看到一個等腰三角形，只需簡單應(yīng)用判定定理(直觀水平);在圖8中，直觀看到有3個等腰三角形，但2個陰影三角形必須應(yīng)用判定定理進行推理論證(簡單推理水平);在圖9中，必須綜合應(yīng)用判定定理和性質(zhì)定理，才能得出線段間的關(guān)系(綜合應(yīng)用定理水平).通過有層次的推進，使學(xué)生分步解決問題，積累了數(shù)學(xué)論證的活動經(jīng)驗和策略.

人的認(rèn)識往往是從特殊到一般然后又到特殊的過程，課堂教學(xué)的有層次遞進正是基于數(shù)學(xué)知識的結(jié)構(gòu)和人的認(rèn)識的這一規(guī)律，加上學(xué)生在學(xué)習(xí)準(zhǔn)備上的差異性，教學(xué)的層次性使得不同學(xué)習(xí)水平的學(xué)生在教學(xué)進程的各個階段各有所獲，這是一種適合學(xué)生的教育.

2 利用過程性變式，彰顯概念建構(gòu)過程

數(shù)學(xué)概念是對數(shù)學(xué)研究對象的高度抽象和概括，是導(dǎo)出數(shù)學(xué)定理法則的邏輯基礎(chǔ)，是構(gòu)建數(shù)學(xué)理論大廈的基石.在概念教學(xué)中，教師要精心創(chuàng)設(shè)情景，讓學(xué)生像數(shù)學(xué)家那樣去“想數(shù)學(xué)”，使數(shù)學(xué)概念的形成過程成為發(fā)現(xiàn)、創(chuàng)新的過程.

案例2 “同類項”概念形成過程的教學(xué)

在同類項概念學(xué)習(xí)過程中，掌握同類項概念的本質(zhì)屬性和非本質(zhì)屬性是教學(xué)的重點，引導(dǎo)學(xué)生體驗同類項概念的形成過程是教學(xué)的難點.為此，筆者設(shè)計了以下6個環(huán)節(jié).

賽一賽 求代數(shù)式-7x2+12x+6x2-9x+x2-2x-1的值.

(請一位學(xué)生說出一個關(guān)于x的1位(或2位)整數(shù)，教師和另一位學(xué)生比賽，看誰先求出正確答案.)

找一找 以下幾組代數(shù)式有什么相同點?

(1)2x和 -3x;(2)5st和7ts;(3)-0.5x3y2和y2x3;(4)ab2c和 -ab2c.

(2人一小組合作學(xué)習(xí)，教師引導(dǎo)質(zhì)疑，總結(jié)這幾組代數(shù)式的相同點，引出同類項的概念.)

評注在概念引入時，教師要根據(jù)概念類型，為學(xué)生創(chuàng)設(shè)生動形象的教學(xué)情境.根據(jù)七年級學(xué)生的心理規(guī)律，通過“賽一賽”這個師生競賽的方式，能激發(fā)起學(xué)生的求知欲望，增強學(xué)生自主學(xué)習(xí)的內(nèi)驅(qū)力.通過“找一找”的活動過程，達到展示知識形成過程，促進學(xué)生概念形成的目的.

想一想 5a2b與ba2是同類項嗎?為什么?(得出同類項的特點——2個“無關(guān)”：與字母順序無關(guān);與系數(shù)無關(guān).)

(得出同類項的特點——2個“相同”：所含字母相同;相同字母的指數(shù)也相同.另外，所有常數(shù)項也看做同類項.)

評注在概念形成之后，教師要引導(dǎo)學(xué)生對概念作進一步的探討，通過辨析變式和等價深化變式，使學(xué)生對概念有更加深刻的理解，讓學(xué)生既知其然，又知其所以然.

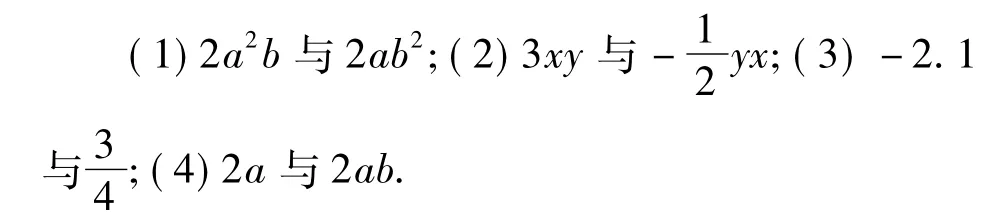
游戲過程：(1)把20張卡片分發(fā)給學(xué)生;(2)教師隨意叫一位學(xué)生，這位學(xué)生高舉自己的卡片;(3)其他學(xué)生觀察自己手中的卡片和這位學(xué)生卡片上的單項式，若認(rèn)為它們是同類項的，也請站起來;(4)每個學(xué)生都是裁判，看看有沒有找錯朋友.

評注鞏固是概念教學(xué)的重要環(huán)節(jié).心理學(xué)原理告訴我們，概念一旦獲得，如不及時鞏固，就會被遺忘.因此，在教學(xué)中要根據(jù)學(xué)習(xí)目標(biāo)和學(xué)習(xí)交流中所反饋的信息，精心選編題目，并選擇適合學(xué)生現(xiàn)狀的學(xué)習(xí)活動方式，讓學(xué)生在解答、變式、探索中，深化對概念的理解，促進認(rèn)知結(jié)構(gòu)的內(nèi)化過程，培養(yǎng)學(xué)生創(chuàng)造性的思維品質(zhì).

3 利用過程性變式，提升例題教學(xué)價值

例題教學(xué)是數(shù)學(xué)課堂教學(xué)的重要環(huán)節(jié)之一，通過例題，學(xué)生對所學(xué)的概念、定理、公式、法則、方法和思想等，可以獲得更進一步的認(rèn)識.同時，又可啟迪學(xué)生思維，示范學(xué)生解題，培養(yǎng)學(xué)生能力.因此，在例題教學(xué)中，若能啟發(fā)學(xué)生多角度、多層次、全方位地思考，并對例題進行變式、探索、推廣和引申，充分挖掘例題的潛在功能，則必能更有效地開發(fā)學(xué)生智力，培養(yǎng)創(chuàng)新意識，提高解題水平，充分發(fā)揮例題的教學(xué)價值.

案例3 一道經(jīng)典習(xí)題的變式教學(xué)

玩一玩 游戲名稱：“找同類項朋友”.

游戲目的：培養(yǎng)學(xué)生主動參與、積極合作、勇于探究的精神，并鞏固同類項概念.

游戲材料：20張卡片，卡片上寫著單項式，如

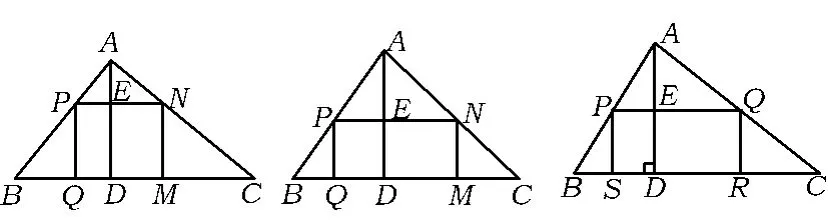
圖10 圖11 圖12

例2 如圖10，有一塊三角形余料ABC，它的邊BC為12 cm，高AD為8 cm.要把它加工成正方形零件，使正方形的一邊在BC上，其余2個頂點分別在AB，AC上.問正方形零件的邊長是多少?

變式1 如圖11，將例2中“正方形PQMN”改為“矩形PQMN”，其他條件不變.矩形的長和寬分別為多少時，所截得的矩形面積最大?最大面積是多少?

變式2 如圖11，一塊鐵皮呈現(xiàn)銳角三角形，它的邊BC為12 cm，高AD為8 cm，要求加工成的矩形一邊在BC上，另外2個頂點在AB，AC上.

(1)試問：這個三角形能否加工成一個面積為24 cm2的矩形零件?能否加工成一個面積為32 cm2的矩形零件?理由是什么?

(2)從第(1)小題的結(jié)論中，試猜想這個三角形內(nèi)接的矩形面積與原三角形面積有何關(guān)系?不需要說明理由.

若從內(nèi)接矩形和原三角形面積之間的關(guān)系考慮，不妨設(shè)△APQ的面積與矩形PQRS面積相等，于是有：

變式3 如圖11，在△ABC中，點P，N分別在AB，AC上，點 Q，M 在 BC上，四邊形 PQMN是矩形，若矩形PQMN的面積與△APN的面積相等，求PN ∶BC的值.

若將變式3所求的結(jié)論與已知條件調(diào)換，則有：

變式4 如圖11，在△ABC中，點P，N分別在AB，AC上，點 Q，M 在 BC上，四邊形 PQMN是矩形，若 PN ∶BC=2 ∶3，求矩形 PQMN面積與△APN的面積比值.

由于例2中△ABC的形狀不確定，不妨把△ABC設(shè)為直角三角形，令∠BAC=90°，有：

變式5 如圖 12，一塊鐵皮呈三角形，∠BAC=90°，要把它加工成矩形零件，使矩形一邊位于BC上，另外2個頂點分別在邊AB，AC上.試問：PS，BS，CR之間有何關(guān)系?為什么?

變式6 一塊直角三角形木板的一條直角邊AB 長為1.5 m，面積為1.5 m2，工人師傅要把它加工成一個面積最大的正方形桌面，請甲、乙2位同學(xué)設(shè)計加工方案，甲設(shè)計方案如圖13所示，乙設(shè)計方案如圖14所示.你認(rèn)為哪位同學(xué)設(shè)計的方案較好?試說明理由(加工損耗忽略不計，計算結(jié)果可保留分?jǐn)?shù)).

圖13 圖14 圖15

變式7 已知△ABC是直角三角形，∠ACB=90°，AC=80，BC=60，如圖 15 所示，把邊長分別為x1，x2，x3，…，xn的 n 個正方形依次放入△ABC 中，則第1個正方形的邊長x1= ______;第n個正方形的邊長xn= ______(用含n的式子表示，n≥1).

變式8 在Rt△ABC中，∠ACB=90°，AC=4，BC=3.

(1)如圖16，四邊形DEFG為Rt△ABC的內(nèi)接正方形，求正方形的邊長;

(2)如圖17，三角形內(nèi)有并排的2個相等的正方形，它們組成的矩形內(nèi)接于Rt△ABC，求正方形的邊長;

(3)如圖18，三角形內(nèi)有并排的3個相等的正方形，它們組成的矩形內(nèi)接于Rt△ABC，求正方形的邊長;

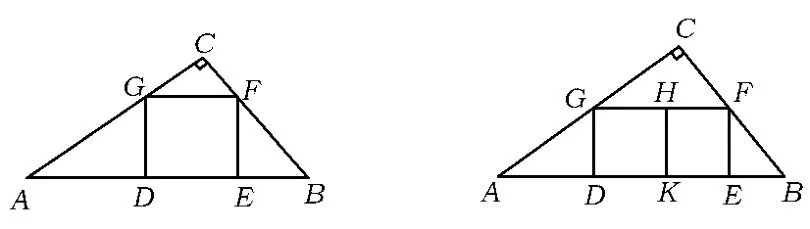
圖16 圖17

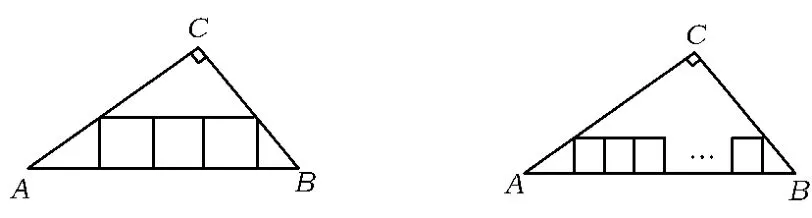
圖18 圖19

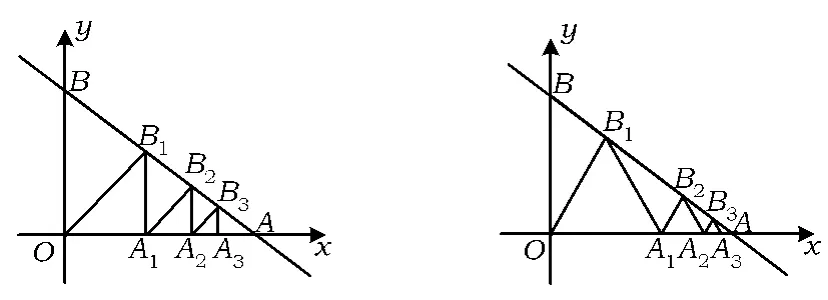
圖20 圖21

(4)如圖19，三角形內(nèi)有并排的n個相等的正方形，它們組成的矩形內(nèi)接于Rt△ABC，求正方形的邊長.變式9 如圖20，在直線y=-x+60與x軸、y軸所圍成的△AOB中，依次放入腰長分別為x1，x2，x3，…，xn的 n 個等腰直角三角形，則 x1=_______，xn= ______(或求 A1，A2，A3，…，An的橫坐標(biāo)).

若把條件“等腰直角三角形”改變?yōu)椤暗冗吶切巍保瑒t有：

變式10 如圖21，在直線y=-x+60與x

軸、y軸所圍成的△AOB中，依次放入邊長分別為x1，x2，x3，…，xn的 n 個等邊三角形，試猜想第 n 個等邊三角形的邊長.

進一步，把“直線”這個條件改變?yōu)椤半p曲線”或者“拋物線”，就有下面的變式：

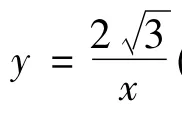
nnn△P1OA1，△P2A1A2，△P3A2A3，…，△PnAn-1An都是等邊三角形，邊 OA1，A1A2，A2A3，…，An-1An都在 x軸上.

(1)求點P1的坐標(biāo);

(2)求y1+y2+y3+…+yn的和.

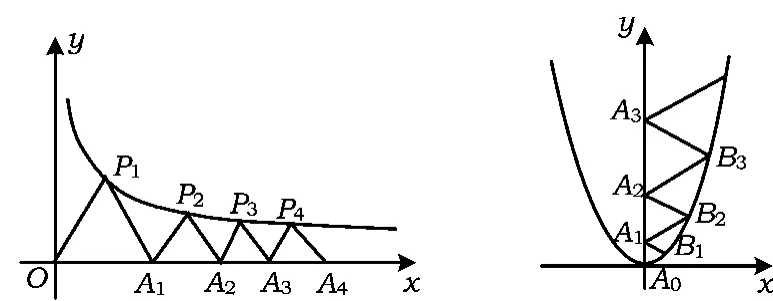
圖22 圖23

［1］ 周成平.中國著名教師的精彩課堂(初中數(shù)學(xué)卷)［M］.南京：江蘇人民出版社，2009.

［2］ 顧泠沅，楊玉東.過程性變式與數(shù)學(xué)課例研究［J］.上海中學(xué)數(shù)學(xué)，2007(1/2)：1-5.