基于EKF的無(wú)位置傳感器永磁同步陀螺電機(jī)控制方法的研究
黃曉凡
(北京市普利門(mén)電子科技有限公司,北京 100041)
0 引言
永磁同步陀螺電機(jī)是航天用陀螺穩(wěn)定平臺(tái)中的關(guān)鍵部件,除了能穩(wěn)定運(yùn)行外,快速起動(dòng)是其基本要求。無(wú)位置傳感器的兩相永磁同步陀螺電機(jī)克服了位置傳感器安裝困難、可靠性不高等缺點(diǎn),逐漸得到應(yīng)用。目前其控制方法主要以利用反電勢(shì)過(guò)零換相控制為主,其他如基于狀態(tài)觀(guān)測(cè)器方法和擴(kuò)展卡爾曼濾波方法(EKF)等還處于研究階段。實(shí)時(shí)計(jì)算量大是EKF的主要缺點(diǎn),運(yùn)算能力強(qiáng)大的DSP可以有效解決這一問(wèn)題。對(duì)陀螺電機(jī)而言,起動(dòng)快速性是衡量控制系統(tǒng)性能的一個(gè)重要方面[1],而起動(dòng)快速性的前提是轉(zhuǎn)子位置信號(hào)的快速獲得。如果EKF能快速收斂,也就是說(shuō),迅速給出正確的轉(zhuǎn)子位置信號(hào),就給電機(jī)的快速起動(dòng)提供了基本條件。
本文以ADI公司的電機(jī)專(zhuān)用DSP控制芯片ADMC300為主控芯片[2],詳細(xì)論述如何將 EKF應(yīng)用于無(wú)位置傳感器的兩相永磁同步陀螺電機(jī)起動(dòng)及穩(wěn)態(tài)運(yùn)行控制中,并論述了相應(yīng)的軟硬件設(shè)計(jì)。試驗(yàn)結(jié)果表明,在不帶位置傳感器的情況下,利用EKF法能有效實(shí)現(xiàn)永磁同步陀螺電機(jī)的自起動(dòng),而且EKF法在起動(dòng)的快速性及獲轉(zhuǎn)子取位置信號(hào)的完整性方面比利用反電勢(shì)過(guò)零換相法[3]更優(yōu)越。
1 無(wú)位置傳感器兩相永磁同步陀螺電機(jī)數(shù)學(xué)模型
1.1 兩相永磁同步陀螺電機(jī)靜止α-β軸數(shù)學(xué)模型
對(duì)兩相永磁同步陀螺電機(jī)而言,其兩相定子繞組(a相和b相)在空間正交,構(gòu)成靜止α-β坐標(biāo)系,其中a相軸線(xiàn)與α軸重合,b相軸線(xiàn)與β軸重合。轉(zhuǎn)子上裝有表貼式的磁鋼。對(duì)永磁陀螺電機(jī)而言,屬于空載運(yùn)行,因此負(fù)載轉(zhuǎn)矩為0。
電機(jī)狀態(tài)空間方程為
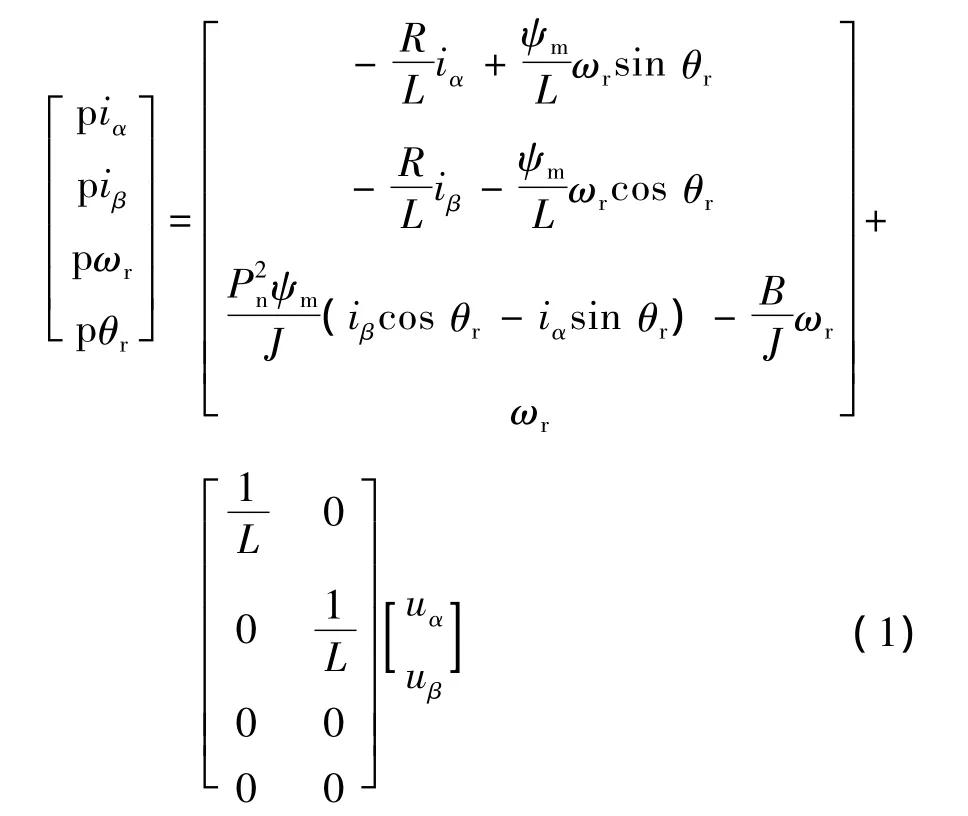
兩相定子繞組反電勢(shì)分別為
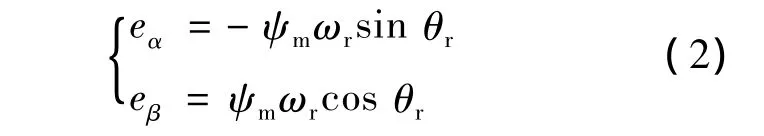
式中:uα、uβ、iα、iβ、eα、eβ——分別為 α-β 軸上的兩相定子電壓、電流、反電勢(shì);
ψm——轉(zhuǎn)子磁璉;
R——兩相定子繞組電阻(兩相定子繞組電阻相等);
L——兩相定子繞組電感(兩相定子繞組電感相等);
ωr——轉(zhuǎn)子電角速度;
θr——轉(zhuǎn)子電角度;
Pn——電機(jī)極對(duì)數(shù);
J——電機(jī)轉(zhuǎn)子轉(zhuǎn)動(dòng)慣量;
B——阻尼系數(shù);
p——微分算子,p=d/dt。
本文中轉(zhuǎn)子位置信號(hào)即是指轉(zhuǎn)子電角度信號(hào)θr。
1.2 基于EKF的離散化兩相永磁同步陀螺電機(jī)數(shù)學(xué)模型
在陀螺電機(jī)中,由于機(jī)械時(shí)間常數(shù)遠(yuǎn)大于電氣時(shí)間常數(shù),可以認(rèn)為一個(gè)EKF采樣濾波周期內(nèi)ωr不變[4],即 pωr=0(注意:不是指整個(gè)調(diào)速范圍內(nèi)ωr不變)。
選取X= [eα,eβ,ωr]T為狀態(tài)變量,根據(jù)式(1)、式(2),并應(yīng)用一個(gè)采樣濾波周期內(nèi)ωr不變的條件,建立電機(jī)的系統(tǒng)方程及測(cè)量方程。
系統(tǒng)方程為
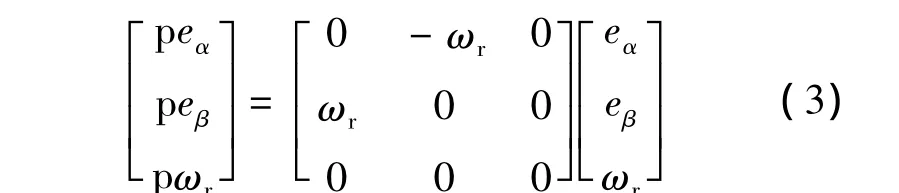
測(cè)量方程為
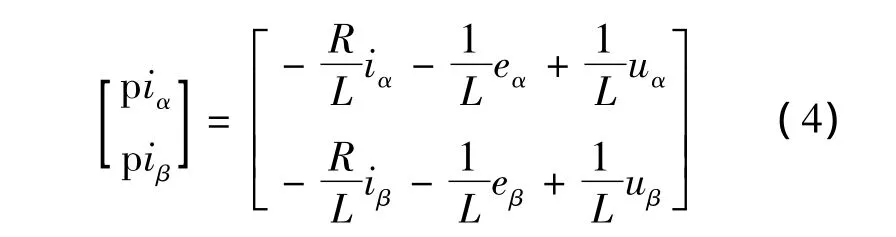
對(duì)式(3)進(jìn)行離散化后得

對(duì)式(4)進(jìn)行離散化后得

式(5)和式(6)稱(chēng)為離散化系統(tǒng)方程,ωk為系統(tǒng)噪聲。式(7)和式(8)稱(chēng)為離散化測(cè)量方程,兩相定子電壓、電流(uα、uβ、iα、iβ)為測(cè)量量,vk為測(cè)量噪聲。Ts為離散采樣濾波周期,ωk、vk為互不相關(guān)的零均值白噪聲。
2 EKF算法
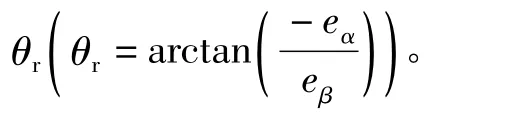
EKF濾波遞推公式計(jì)算步驟如下:
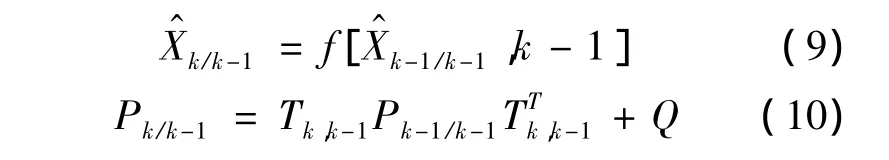
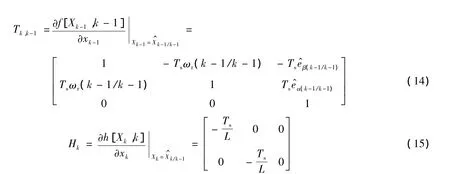
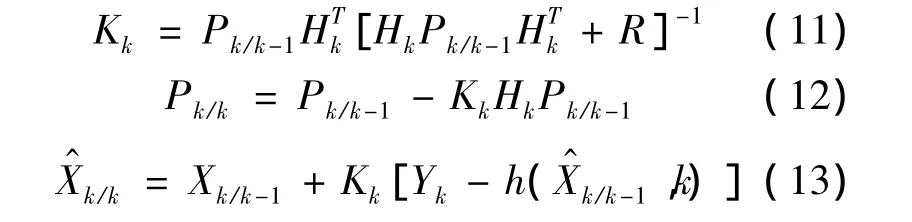
式中:Pk/k-1——一步預(yù)測(cè)均方誤差陣;
Pk/k——估計(jì)均方誤差陣;
Kk——濾波增益陣;
Q——系統(tǒng)噪聲方差陣,要求為非負(fù)定陣;
R——測(cè)量噪聲方差陣,要求為正定陣。
另外:
根據(jù)卡爾曼濾波穩(wěn)定性理論,隨著濾波時(shí)間的增長(zhǎng),狀態(tài)變量估計(jì)值和狀態(tài)變量估計(jì)均方誤差陣Pk/k各自受其初值的影響不大,而Q,R的選取則通過(guò)試驗(yàn)憑經(jīng)驗(yàn)試湊得到。另外,EKF是用線(xiàn)性化模型來(lái)近似原來(lái)的非線(xiàn)性模型,其近似程度可衡量如下:當(dāng)濾波器已投入工作時(shí),Pk/k的跡tr[Pk/k]是可以獲得的,它反映了狀態(tài)變量估計(jì)誤差值‖Xk/k-‖的大小,可作為濾波近似程度的一種量度。
基于此,本文P0、X0、Q及R取值如下,而EKF的采樣濾波周期經(jīng)調(diào)試定為T(mén)s=200 μs。
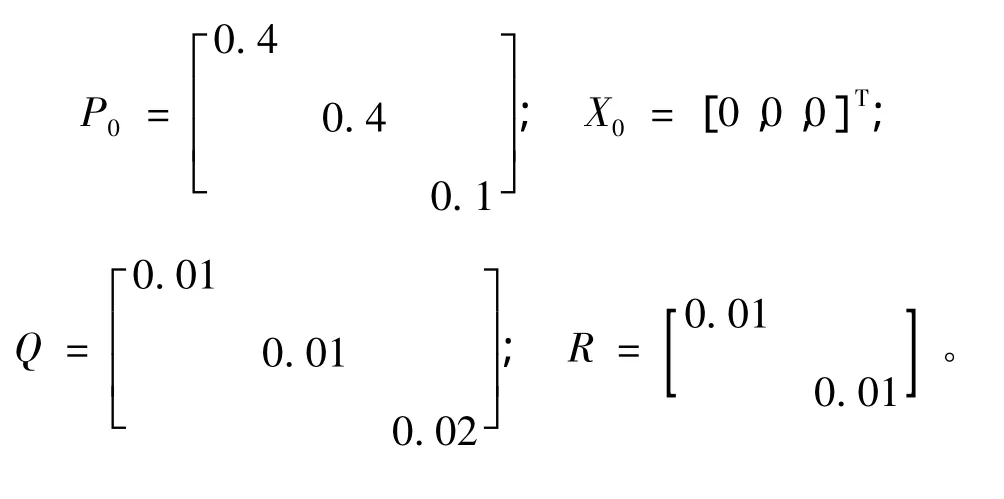
3 控制系統(tǒng)硬件設(shè)計(jì)
控制系統(tǒng)硬件部分見(jiàn)圖1。主要由兩相永磁同步電機(jī)、兩相橋式功率逆變電路、電壓電流傳感器和基于DSP的高性能電機(jī)控制芯片ADMC300組成。其中ADMC300是核心,負(fù)責(zé)電壓電流數(shù)字采樣,EKF,Park逆變換等控制程序的執(zhí)行。
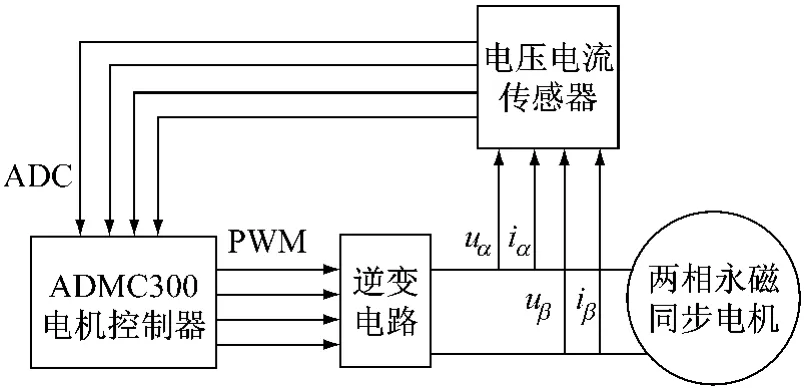
圖1 控制系統(tǒng)硬件圖
ADMC300的PWM單元產(chǎn)生四路PWM信號(hào)輸出(AH/AL、BH/BL),分別與相應(yīng)的兩相橋式功率逆變電路的 PWM輸入端相連,為其提供PWM信號(hào)。兩相橋式功率逆變電路則在PWM信號(hào)作用下為電機(jī)兩相定子提供所需的電壓。電壓、電流傳感器的副邊輸出則與ADMC300的模數(shù)轉(zhuǎn)換單元(ADC)的輸入端相連,為ADC單元提供電機(jī)兩相定子電壓、電流的采樣值。
4 控制系統(tǒng)軟件設(shè)計(jì)
采用id=0的矢量控制方案[6]。其工作原理如下:通過(guò)電機(jī)兩相電壓、電流的檢測(cè),利用EKF程序得到電機(jī)轉(zhuǎn)子位置信號(hào)θr,經(jīng)Park逆變換程序把指令電流轉(zhuǎn)化為兩相繞組指令電流,,分別與采樣的電流值i,i比較,通過(guò)電流調(diào)
αβ節(jié)程序,控制輸入到兩相橋式功率逆變電路的PWM信號(hào)占空比,使實(shí)際電流跟蹤指令電流。
利用ADMC300匯編語(yǔ)言編制EKF,Park逆變換,電流調(diào)節(jié),電壓、電流采樣等程序,構(gòu)成系統(tǒng)的軟件部分,程序流程圖見(jiàn)圖2。對(duì)各部分分別簡(jiǎn)介如下。
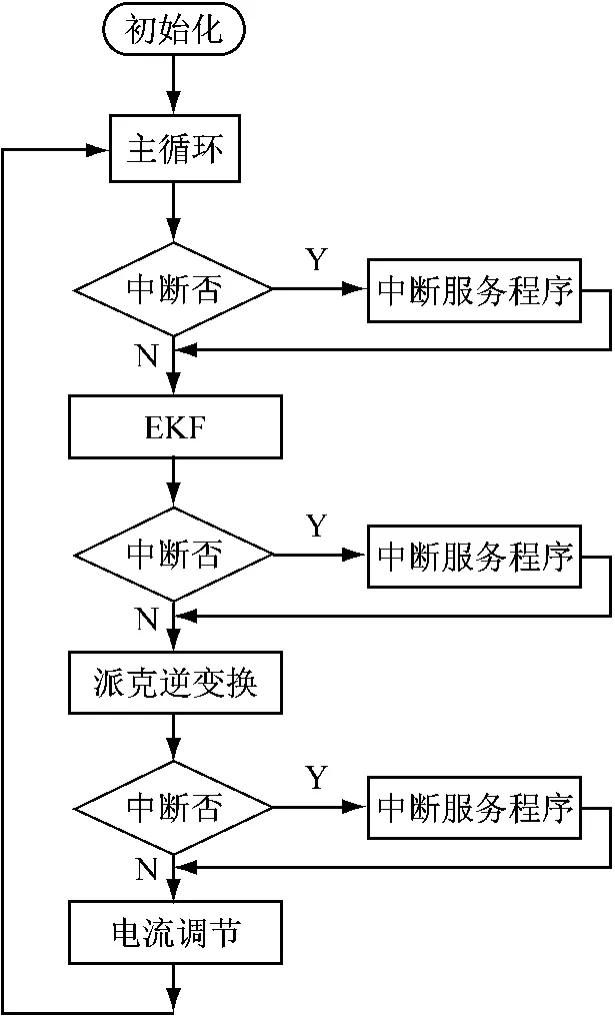
圖2 控制系統(tǒng)軟件流程圖
(1)初始化。完成ADC單元校正,開(kāi)ADC單元及PWM單元中斷,設(shè)置PWM單元參數(shù)等。
(2)主循環(huán)。主循環(huán)是一個(gè)無(wú)限循環(huán)體,在每一個(gè)循環(huán)中,依次執(zhí)行以下程序:EKF;Park逆變;電流調(diào)節(jié)。
(3)Park逆變換。
在id=0矢量控制方案下,Park逆變換式簡(jiǎn)化為
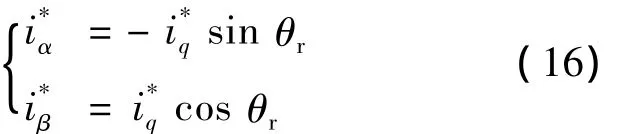
5 試驗(yàn)結(jié)果與分析
試驗(yàn)用永磁陀螺電機(jī)為兩相定子,五對(duì)轉(zhuǎn)子磁極(采用表面貼裝式),其參數(shù)如下:兩相電感Lα=Lβ=L=45 μH,兩相電阻Rα=Rβ=R=5 Ω,轉(zhuǎn)子磁鏈 ψm=0.003 V·S/rad。
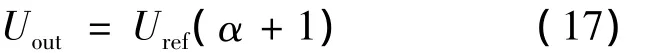
式中:Uref——ADMC300提供的2.5 V參考電壓;
α——數(shù)字輸入量,為定點(diǎn)格式;
Uout——模擬輸出量。
5.1 電機(jī)起動(dòng)過(guò)程中EKF收斂性驗(yàn)證
圖3是電機(jī)從靜止開(kāi)始起動(dòng)過(guò)程中EKF給出的轉(zhuǎn)子電角度信號(hào)估計(jì)值(D/A轉(zhuǎn)換后的模擬量,下同),圖 4 是Pk/k的跡tr[Pk/k]隨時(shí)間變化圖。可以看出經(jīng)過(guò)約350 ms,tr[Pk/k]從初值 0.9(對(duì)應(yīng)圖2中約4.5 V)穩(wěn)定在一個(gè)小值0.005(對(duì)應(yīng)圖中約2.5 V)。這說(shuō)明EKF開(kāi)始收斂,給出EKF意義上的最優(yōu)估計(jì)值。
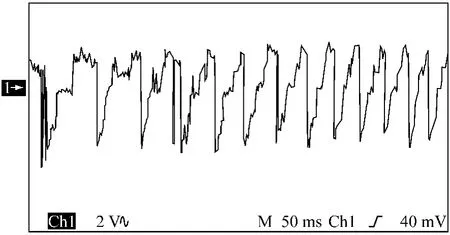
圖3 電機(jī)起動(dòng)過(guò)程中EKF給出的波形圖
5.2 電機(jī)穩(wěn)定運(yùn)行過(guò)程中EKF估計(jì)轉(zhuǎn)子位置信號(hào)正確性的驗(yàn)證
(1)反電勢(shì)估計(jì)值與轉(zhuǎn)子電角度信號(hào)估計(jì)值波形。

圖4 電機(jī)起動(dòng)過(guò)程中tr[Pk/k]波形圖
圖5和圖6給出了通過(guò)調(diào)節(jié)指令電流,使電機(jī)分別穩(wěn)定在910 r/min及4 620 r/min下的反電勢(shì)估計(jì)值與轉(zhuǎn)子電角度信號(hào)估計(jì)值波形圖。
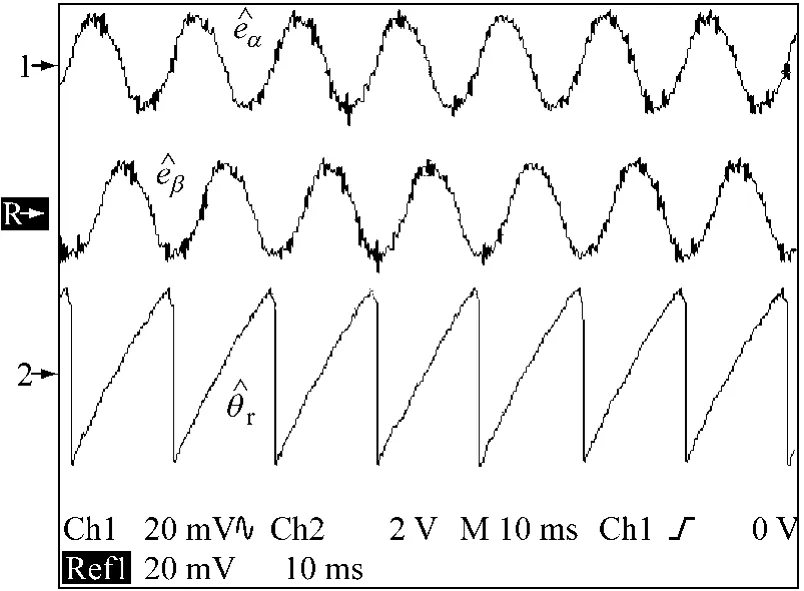
圖 5 910 r/min 下 EKF 給出的及波形圖
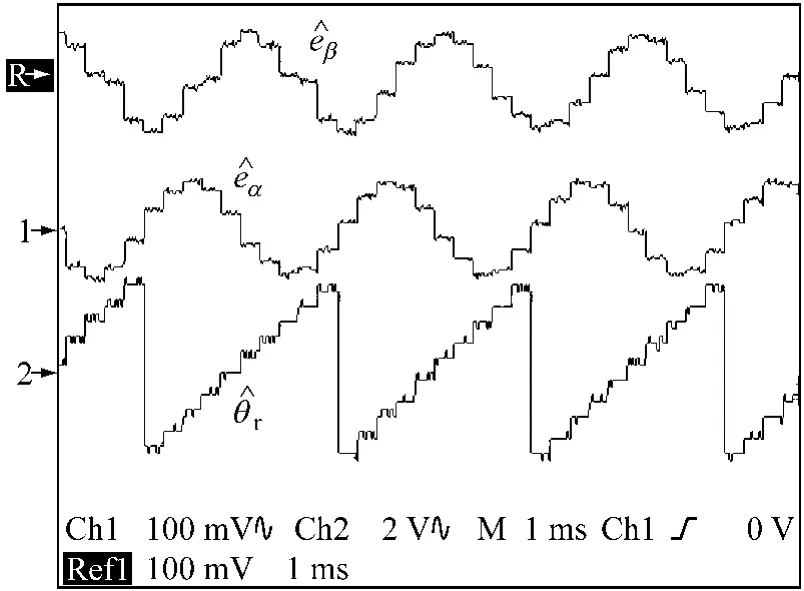
圖 6 4 620 r/min 下 EKF 給出的及波形圖
由圖5、圖6可以看出三者相位對(duì)應(yīng)關(guān)系正確(A相反電勢(shì)eα應(yīng)超前B相反電勢(shì)eβ90°電角度),并且轉(zhuǎn)速越低,估計(jì)出的離散位置信號(hào)越密集,宏觀(guān)意義上看越接近于獲得連續(xù)位置信號(hào)。反電勢(shì)過(guò)零換相法只能在一個(gè)電周期內(nèi)估計(jì)出4個(gè)反電勢(shì)過(guò)零時(shí)的轉(zhuǎn)子位置信號(hào)。
(2)EKF估計(jì)轉(zhuǎn)子電角度信號(hào)正確性的驗(yàn)證。
下面分析如何從A相電壓uα波形中提取出A相反電勢(shì)eα波形。在PWM調(diào)壓下,由于電機(jī)電感較小(45 μH),電流會(huì)出現(xiàn)斷續(xù)情況,檢測(cè)到的電機(jī)A相電壓信號(hào)主要由兩部分組成:對(duì)應(yīng)A相繞組晶體管導(dǎo)通、A相繞組電流不為零時(shí)加在逆變橋上的直流電壓,以及對(duì)應(yīng)A相繞組晶體管截止(包括序流過(guò)程)后、A相繞組電流為零時(shí)的反電勢(shì)。利用PWM信號(hào)關(guān)斷期間、A相繞組電流為零時(shí)的反電勢(shì),即可得到大量離散的電機(jī)A相實(shí)際反電勢(shì)信號(hào)eα。圖7給出了A相電壓信號(hào)uα波形構(gòu)成圖,其小圓圈中所示均為反電勢(shì)信號(hào)eα,當(dāng)示波器的Display Style檔打在Dots模式下可以更清楚地看出eα波形。
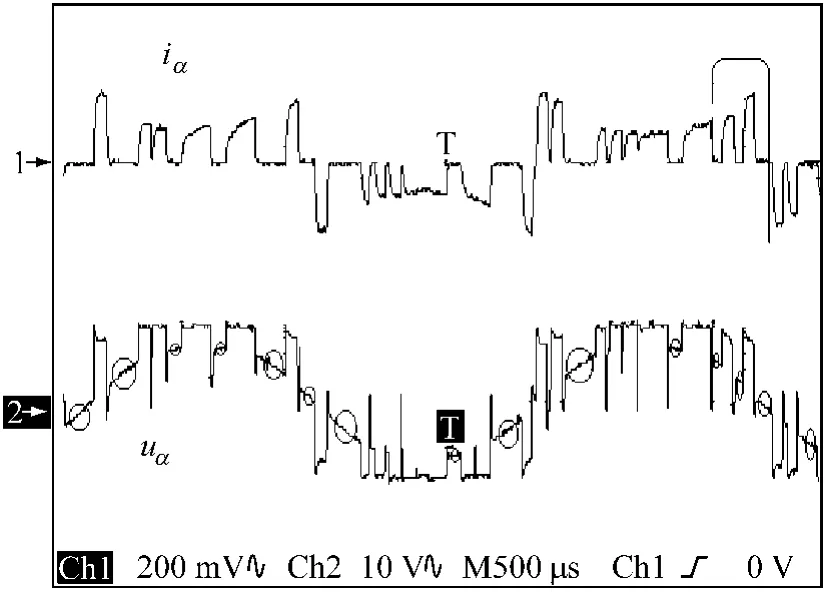
圖7 A相電壓信號(hào)uα波形構(gòu)成圖
圖8和圖9給出了2 860 r/min下的電機(jī)A相實(shí)測(cè)電壓uα及A相反電勢(shì)估計(jì)值波形對(duì)比圖。圖9中CH2(uα)波形中間的接近正弦波的那條虛線(xiàn)即是電機(jī)A相實(shí)際反電勢(shì)eα。可見(jiàn)eα與A相反電勢(shì)估計(jì)值吻合。由圖5和圖6知道B相實(shí)際反電勢(shì)eβ與B相反電勢(shì)估計(jì)值也必然吻合,由此可知EKF估計(jì)的轉(zhuǎn)子電角度信號(hào)是正確的。
5.3 電機(jī)的起動(dòng)性能對(duì)比試驗(yàn)
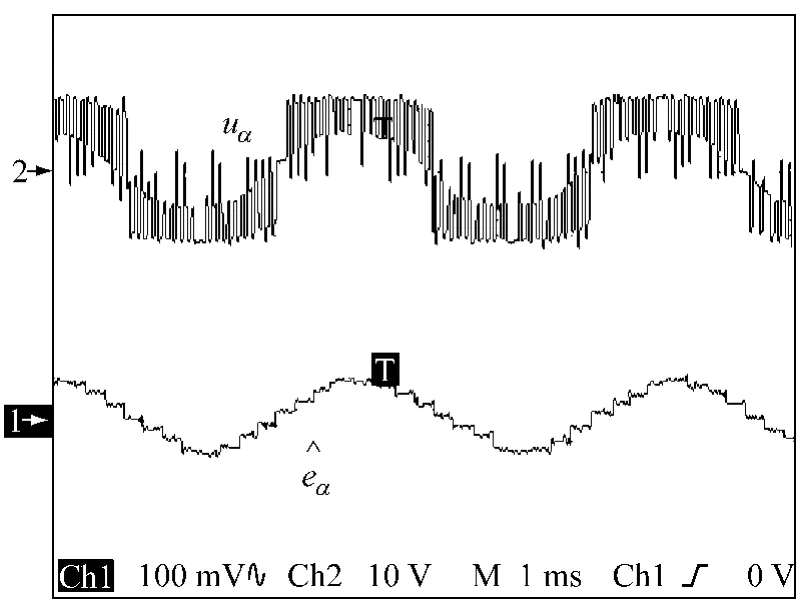
圖8 2 860 r/min下的電機(jī)A相電壓uα與A相反電勢(shì)估計(jì)值波形對(duì)比圖
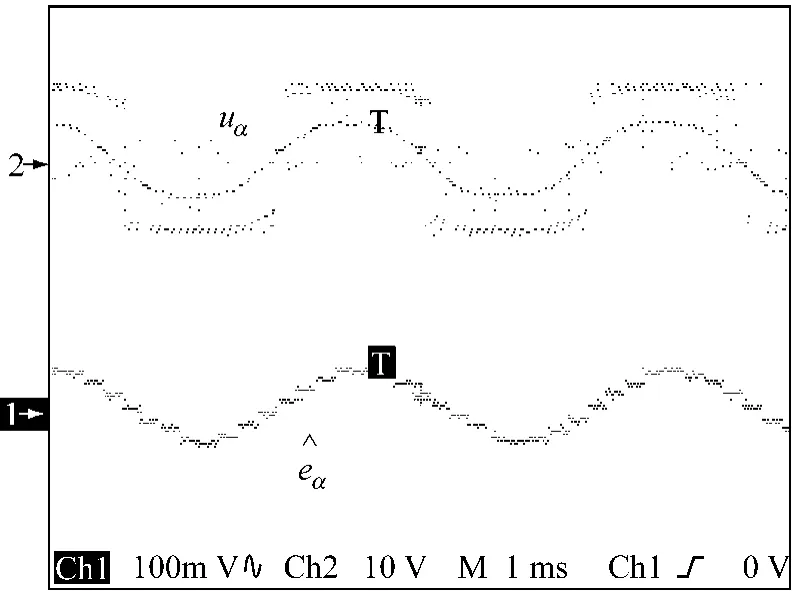
圖9 2 860 r/min下的電機(jī)A相電壓uα與A相反電勢(shì)估計(jì)值波形對(duì)比圖(示波器的Display Style檔打在Dots模式下)
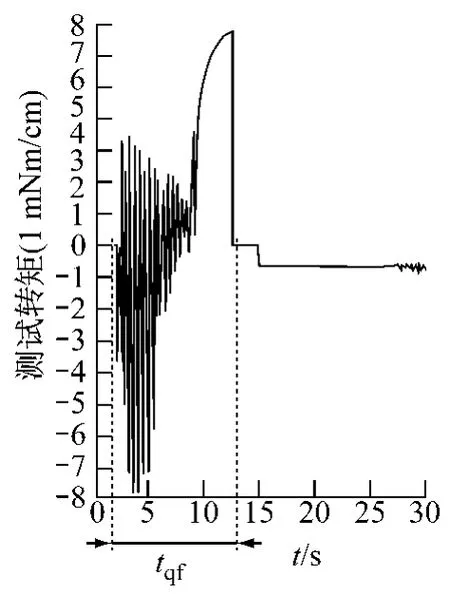
圖10 反電勢(shì)過(guò)零換相法電機(jī)起動(dòng)性能
利用反作用力矩測(cè)試儀[1],圖10和圖11給出了同樣起動(dòng)電流下(0.6 A),到達(dá)同樣轉(zhuǎn)速(5 000 r/min)下,分別利用反電勢(shì)過(guò)零換相法和EKF法的電機(jī)起動(dòng)性能對(duì)比試驗(yàn)。根據(jù)反作用力矩測(cè)試儀原理可知,當(dāng)電機(jī)處于穩(wěn)定轉(zhuǎn)速時(shí),反作用力矩測(cè)試儀測(cè)試轉(zhuǎn)矩讀數(shù)為零。由圖10可知反電勢(shì)過(guò)零換相法起動(dòng)用了tqf=9 s,其中變頻起動(dòng)加速時(shí)間為6 s,獲得可靠反電勢(shì)信號(hào)后閉環(huán)控制加速時(shí)間為3 s。由圖11可知EKF法起動(dòng)只用了tqe=3 s。
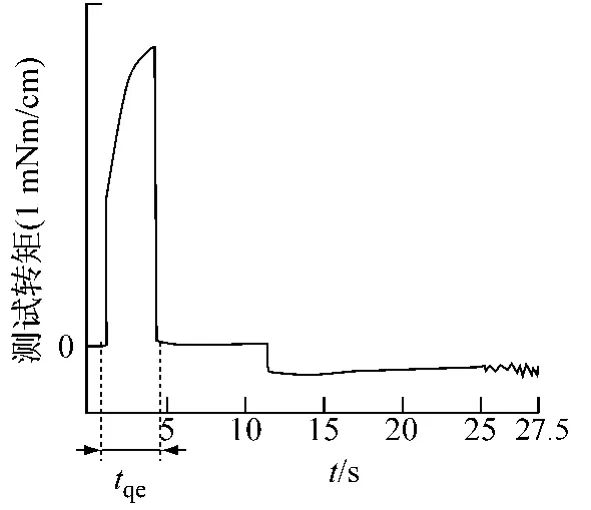
圖11 EKF法電機(jī)起動(dòng)性能
6 結(jié)語(yǔ)
試驗(yàn)結(jié)果表明,在不帶位置傳感器的情況下,利用EKF法能有效實(shí)現(xiàn)永磁同步陀螺電機(jī)的自起動(dòng),而且EKF法在起動(dòng)的快速性及獲取轉(zhuǎn)子位置信號(hào)的完整性方面比利用反電勢(shì)過(guò)零換相法更優(yōu)越。
[1]陸元九.慣性器件(上][M].北京:宇航出版社,1990.
[2]吳敏淵,金偉正,胡志雄,等.ADSP系列數(shù)字信號(hào)處理器原理[M].北京:電子工業(yè)出版社,2002.
[3]沈建新,呂曉春,杜軍紅,等.無(wú)傳感器無(wú)刷直流電機(jī)三段式起動(dòng)技術(shù)的深入分析[J].微特電機(jī),1998(5):8-11.
[4]王東旭,王莉,李大喜,等.基于EKF的感應(yīng)電動(dòng)機(jī)無(wú)速度傳感器調(diào)速系統(tǒng)改進(jìn)研究[J].微特電機(jī),2009(8):33-35.
[5]秦永元,張洪鉞,汪淑華.卡爾曼濾波與組合導(dǎo)航原理[M].西安:西北工業(yè)大學(xué)出版社,1998.
[6]景軍鋒,康雪娟.基于DSP的永磁同步電機(jī)全數(shù)字變頻調(diào)速控制系統(tǒng)的設(shè)計(jì)[J].電機(jī)與控制應(yīng)用,2010,37(2):43-46.

