基于自適應擴展卡爾曼濾波器的永磁同步電機超低速控制*

丁信忠， 張承瑞，2， 李虎修， 于樂華， 胡天亮，2

(1.山東大學機械工程學院，山東濟南 250061;

2.山東大學高效潔凈機械制造教育部重點實驗室，山東濟南 250061;

3.山東大學控制科學與工程學院，山東濟南 250061)

0 引言

永磁同步電機(Permanent Magnet Synchronous Motor，PMSM)精確的速度及位置反饋是實現高性能低速控制的重要保證。通常，借助軸向編碼器的采樣計數估算出電機的平均速度。但是，受到編碼器分辨率的限制，在超低速范圍，速度反饋信息容易丟失，如果通過延長采樣周期以保證速度分辨率，將降低速度環的帶寬，且過長的反饋延時將使伺服系統變得不穩定。

目前，瞬時觀測器理論［1］和人工神經網絡［2］被深入研究，并應用于伺服系統狀態估計。基于瞬時觀測器理論的狀態估計方法能夠估計電機的瞬時狀態，具有較好的實時性，但抗干擾能力不佳，在噪聲環境中，位置和速度檢測可能失效［3］。人工神經網絡方法擺脫了對電機模型的依賴，具有良好的魯棒性，但需要大量樣本對神經元的權值和偏置進行訓練，學習時間過長，而且網絡的穩定性和收斂性的證明也比較困難［4］。擴展卡爾曼濾波器(Extended Kalman Filter，EKF)是一種最優隨機狀態估計器，可對非線性時變系統的狀態進行在線估計，并具有較強的抗干擾和平滑噪聲能力，因而適用于非線性、強耦合且高噪聲的伺服驅動系統。隨著嵌入式計算技術的發展，EKF計算量大的問題已被良好解決。

本文提出了一種使用低精度編碼器條件下獲得PMSM良好低速性能的控制方法。其中，EKF用于對電機轉速、角位移和負載轉矩進行瞬時估計，并在估計過程中利用辨識出的敏感參數對估計器的狀態矩陣進行迭代修正，以保證估計器在多種工況下均可獲得滿意的估計結果。估計出的電機瞬時轉速和位置值替代編碼器檢測值進行伺服閉環控制，由此保證電機低速運行下的轉速和位置反饋精度。為驗證該方法的有效性，本文設計仿真和試驗與使用改進型M/T速度檢測方法［5］下的低速控制性能進行了對比。

1 EKF瞬時狀態估計器

1.1 估計器建模

在未飽和狀態下，PMSM的電壓方程為

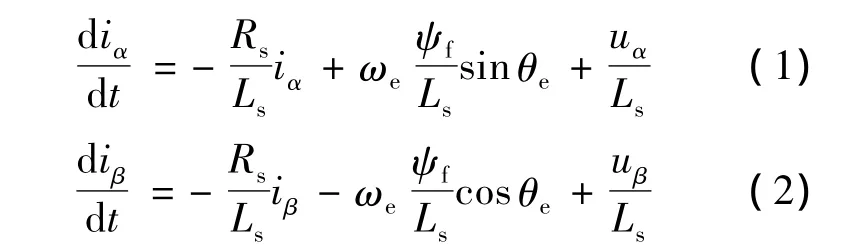
式中:iα、iβ、uα和uβ——分別為定子電流、電壓在Clarke坐標系下α、β軸的分量;

Rs——定子相電阻;

Ls——等效同步電感;

ψf——永磁體基波磁鏈;

ωe——轉子電角速度;

θe——電角位移。

轉子和所帶負載組成機械子系統，根據牛頓定律，可得PMSM的轉矩平衡方程為

式中:np——電機極對數;

J——系統轉動慣量，其中包括電機轉子及負載折算到電機軸上的轉動慣量;

B——黏滯摩擦系數;

Te——電機輸出的電磁轉矩;

Tl——等效負載轉矩，其中包括負載轉矩以及由于黏滯摩擦系數非線性變化、電流給定偏差等因素造成的轉矩波動。

由于電流環的采樣頻率遠高于等效負載轉矩變化的頻率，故可認為負載轉矩在一個采樣周期內保持不變，即

聯合式(1)～式(4)，得到狀態估計器的狀態方程和輸出方程，即

式中:x——狀態矢量，即預估計量;

u——輸入矢量;

y——輸出矢量。

狀態函數f(x)是狀態矢量和輸入矩陣的耦合項。

實際系統中，需要考慮由于估計模型不準確和外界干擾等不利因素造成的影響，因此在EKF的狀態方程和輸出方程中分別引入系統噪聲矩陣V和測量噪聲矩陣W，并將估計方程離散化以便用于數字控制系統，可得

式中:x(k)、u(k)、y(k)和f［x(k)］——分別為狀態矢量、輸入矢量、輸出矢量和狀態函數的離散形式;

V(k)和W(k)——分別為離散化的系統噪聲矢量和測量噪聲矢量。

通常，系統噪聲和測量噪聲為零均值高斯白噪聲，由此可得到EKF算法中需要的噪聲協方差對角矩陣Q和R，即

式中:Qi——定子電流系統噪聲協方差值;

Qω、Qθ和QT——分別為轉子電角速度、電角位移和負載轉矩的系統噪聲協方差值;

Ri——定子電流測量噪聲協方差值;

Rθ——轉子電角位移測量噪聲協方差值。綜合以上各式，即得到用于EKF伺服系統狀態估計的狀態模型。

1.2 EKF狀態估計與魯棒性分析

基于EKF的伺服系統狀態估計是由第k次的估計結果(k)來獲得第k+1次的估計結果，即由當前的系統狀態來估計下一周期的狀態，從而解決了M/T速度檢測方法速度反饋滯后一個周期的問題，加之算法中綜合考慮了系統噪聲和測量噪聲的影響，因此可以為伺服閉環控制系統提供實時、準確的狀態反饋，有助于提高伺服系統的動、靜態性能。

估計過程分為預測和校正兩大階段，通過以下遞推過程［6］逼近系統真實狀態:

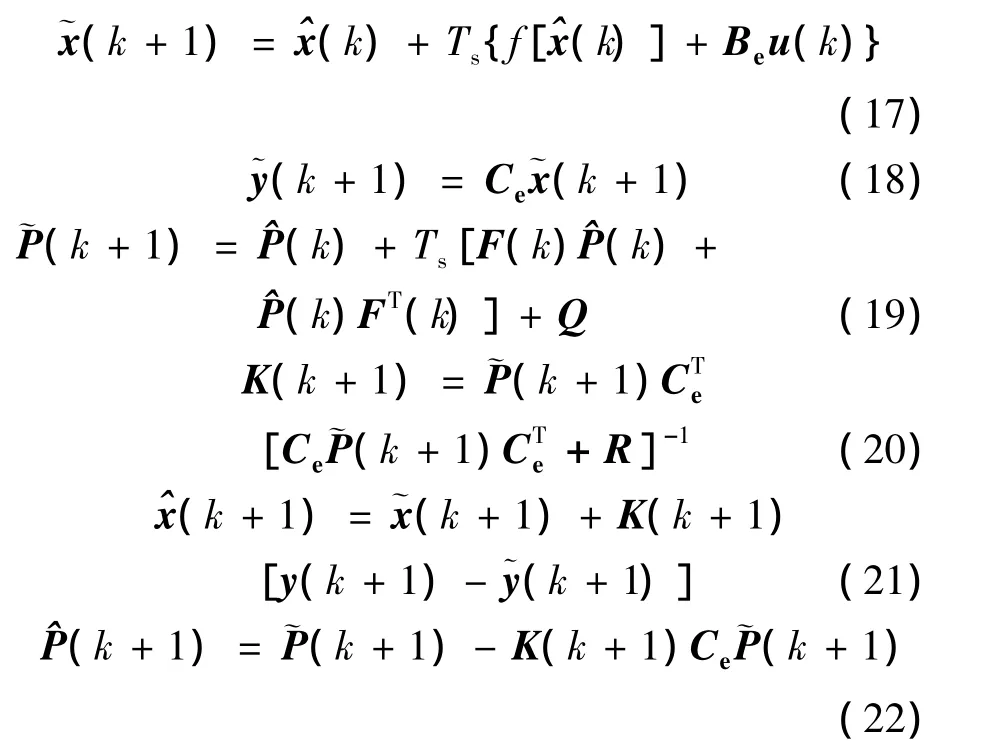
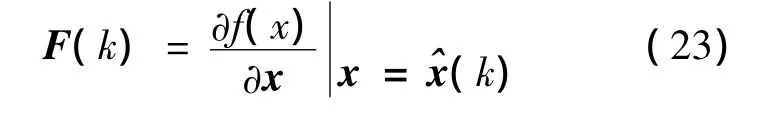
經過以上6個步驟的遞推計算，即可得到本周期內的狀態矢量中的預估計變量值，基于EKF的伺服系統狀態估計過程如圖1所示。

式中:Ts——電流環采樣周期;

?

P?(k)和P^(k)——分別為預測協方差矩陣和估計協方差矩陣。

F(k)為梯度矩陣，定義如下:

圖1 離散擴展卡爾曼濾波器結構圖

當電動機在零速附近運行時，繞組電壓將降到很低，此時電機定子電阻、等效電感及系統轉動慣量J等因素將對系統動態模型產生主要影響，從而影響EKF的估計效果。但是，EKF的系統模型中綜合了定子電流采樣這一因素，在超低速區域，霍爾電流傳感器依舊可以提供準確的電流反饋，從而彌補了繞組電壓過低產生的影響。當負載轉動慣量變化時，EKF的動態性能將相對降低，文獻［7］中指出，無法將轉動慣量變化引起的轉矩脈動等價到等效負載轉矩Tl中，通過轉矩前饋加以改善，且無法通過調整系統噪聲矩陣中轉矩協方差值QT來減小轉動慣量變化對估計精度的影響。

為解決上述問題，在伺服系統狀態估計中，需要對系統的轉動慣量進行在線辨識，并根據辨識結果對EKF的狀態方程系數矩陣進行在線參數自整定。

2 轉動慣量在線辨識

對于表貼型永磁同步電機，將式(3)所示的轉矩平衡方程改寫為

式中:ωm——轉子機械角速度;

Kt——轉矩常數;

iq——交軸電流。

令J'=1/J，T'=Ktiq－Tl，式(24)可簡化為

式(25)中包含待辨識參數J的信息，且與PMSM具有相同的外部激勵輸入iq以及相同的機械轉速ωm輸出。將ωm和J'分別以其估計值^ωm和J^'表示，可得模型參考自適應系統(Model Reference Adaptive System，MRAS)可調模型的微分方程:

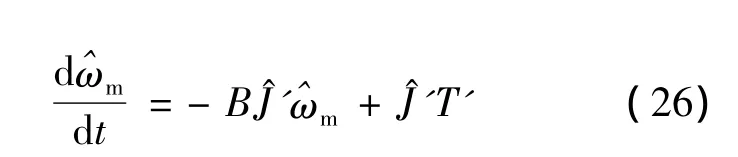
選擇PMSM本身作為參考模型，式(25)為表征參考模型動態特征的差分方程，當方程(26)中的估計值與實際值相等時，差分方程(26)就轉變為表示PMSM本身的真實方程，兩個模型將等價。待辨識參數J^'為MRAS狀態變量，將參考模型的差分方程(25)減去可調模型(26)，可得

式中，e為廣義誤差，定義如下:

對于數字控制系統，伺服電機的電氣時間常數遠小于其機械時間常數，故在一個速度環控制周期內，假定轉子機械轉速ωm和系統轉動慣量J不變。根據式(27)，MRAS辨識系統可等價為一個標準反饋系統，其中包含一個線性時不變前饋子系統和一個非線性時變反饋子系統。

MRAS的關鍵問題之一是自適應機構中所執行的自適應規律的確定。自適應規律保證廣義誤差漸近穩定且待辨識參數收斂到真實值［8］。根據Popov超穩定理論，若保證自適應系統穩定，其中的非線性時變反饋環節需要滿足

其中，F=()();是當t1＞0時不隨時間變化的有限正數。

為了避免廣義誤差趨近于零時算法失效，自適應規律通常設計為比例積分(PI)結構。因此，將預估計量J^'的自適應規律取為PI形式，即

式中，(0)為初始值。將F和式(30)代入式(29)，經推導可得自適應規律:

結合式(27)，MRAS轉動慣量辨識系統的等效非線性結構如圖2所示。依據自適應規律，狀態變量驅動可調模型趨向于參考模型。因此，在廣義誤差趨近于零的過程中待辨識的轉動慣量將逐漸趨近于真實值。

圖2 MRAS參數辨識等效非線性反饋系統

MRAS辨識出的轉動慣量用于在線更新EKF狀態估計器的系統矩陣，從而實現轉動慣量的魯棒控制。EKF估計出的狀態變量中，角速度^ωm和角位移θ^m分別用于速度環和位置環的反饋值，等效負載轉矩T^l用于前饋控制以消除電機轉矩脈動。將轉動慣量自適應EKF狀態估計用于PMSM伺服驅動系統，構成帶有速度估計和轉矩前饋的速度伺服系統，如圖3所示。

圖3 EKF狀態估計速度伺服系統

3 仿真及試驗分析

仿真和試驗中所用PMSM及所帶負載的參數如表1所示。圖4顯示了不同轉動慣量初始值下的轉動慣量辨識結果，其間速度指令和轉矩指令分別在0.15 s和0.3 s時刻階躍變化。可以看出，慣量辨識值快速收斂于真實值，且在轉速和轉矩突變時沒有發生振蕩。

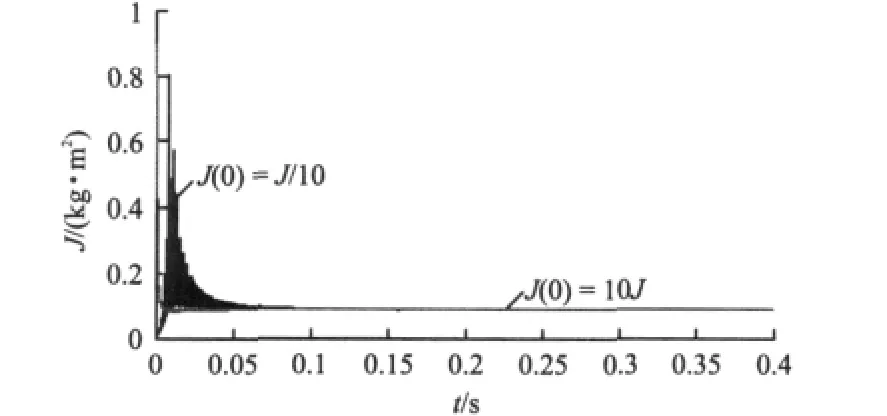
圖4 階躍指令下不同初始值的慣量辨識效果

圖5所示的仿真試驗中，設定速度指令為±100 r/min，負載轉矩恒定在8 N·m。在0.5 s時刻將EKF輸入矩陣中定子電阻修改為準確值的2倍，而同步電感為準確值的1/2，并在1 s和2 s時刻分別將轉動慣量設定為真實值的2倍和1/3。從仿真結果可以看出，當定子電阻和等效電感取值不準確時，估計器并未受到影響。相比之下，從仿真結果可以看出，當EKF系數矩陣中轉動慣量的取值偏離準確值時，電機轉速和轉矩的瞬態估計結果將出現較大的超調和波動。由此可見，EKF估計器對轉動慣量較為敏感，而對電阻和電感具有較好的魯棒性。在實際系統中，需要利用轉動慣量辨識結果對EKF的系數矩陣進行在線整定。

圖5 被控對象電氣參數對估計結果的影響

本文所用試驗系統如圖6所示。電機同軸安裝一個SICK公司生產的32 768線高精度光電編碼器，并連接至專用控制器捕捉倍頻后的編碼器脈沖，測量電機的實時轉速，作為比對參考。其中，速度環和電流環的控制周期分別設定為400 μs和 80 μs，得益于 STM32F4 處理器的強勁性能，轉動慣量辨識、EKF狀態估計以及PI電流控制器的總計算時間約為30 μs，加上約20 μs FOC算法執行時間，所有的電機控制算法可在一個電流環周期內執行完畢。

表1 仿真和試驗中所用電機參數

圖6 試驗平臺配置

圖7所示試驗結果對比了超低速下使用轉動慣量自適應狀態估計器ωest和M/T速度檢測ωenc方法時的電機速度響應。試驗結果表明，在超低速度下，由于編碼器反饋信息的缺失，使用M/T方法時的速度響應趨于不穩定。相比之下，本文提出的方法仍舊能夠提供準確的速度反饋，獲得良好的低速控制性能。

圖8所示為動態轉速響應的對比波形。試驗中，速度給定ωref為頻率70 Hz，幅值20 r/min的正弦指令。使用編碼器檢測轉速作為速度反饋時，速度響應ωenc存在約30°的相位滯后，而使用自適應EKF速度估計作為速度反饋值時，速度響應ωest沒有明顯的相位滯后，動態跟隨特性良好。

4 結語

本文提出了一種使用常規編碼器條件下獲得PMSM良好速度特性的控制方法。仿真和試驗結果表明，當PMSM運行于低速或超低速區域時，本文提出的EKF狀態估計策略依舊可以提供準確、實時的速度反饋，從而在寬調速范圍內實現良好速度控制性能，有效改善了系統的動態性能并增大了調速范圍。此外，通過MRAS在線辨識出的轉動慣量對EKF系數矩陣實施自整定后，自適應EKF估計算法對系統轉動慣量、定子電阻、等效電感的變化以及環境噪聲均有很好的魯棒性，與使用M/T速度檢測方法相比具有調速范圍寬、實時性好及抗干擾能力強等優勢。

［1］WANG M S，KUNG Y S，THI H，et al.Superior low-speed control of a permanent magnet synchronous motor with digital encoder［C］∥Proceedings of the Institution of Mechanical Engineers，PartⅠ:Journal of Systems and Control Engineering，2011，225(2):281.

［2］KARANAYIL B，RAHMAN M F，GRANTHAM C.On-line stator and rotor resistance estimation scheme for vector-controlled induction motordriveusing artificial neural networks［C］∥Industry Applications Conference，2003，38th IAS Annual Meeting，2003:132-139.

［3］HEUI W K，SEUNG K S.A new motor speed estimator using Kalman filter in low-speed range［J］.Industrial Electronics，IEEE Transactions on，1996，43(4):498-504.

［4］楊曉帆，陳廷槐.人工神經網絡固有的優點和缺點［J］.計算機科學，1994(2):23-26.

［5］楊松濤，和麗清，安成斌.DSP在高精度數字式電機測速中的應用［J］.紅外與激光工程，2006(S4):543-548.

［6］王成元，孫宜標，夏加寬，等.電機現代控制技術［M］.北京:機械工業出版社，2006.

［7］TAEG J K，DONG S H.High-performance speed control of electric machine using low-precision shaft encoder［J］.Power Electronics，IEEE Transactions on，1999，14(5):838-849.

［8］ATTAIANESE C，DAMIANO A，GATTO G，et al.Induction motor drive parameters identification［J］.Power Electronics，IEEE Transactions on，1998，13(6):1112-1122.