一種干擾環境下PN 碼自適應捕獲方法研究

楊曉波

（石家莊職業技術學院電子工程系 河北 石家莊 050081）

0 引言

本地PN 碼與接收信號的精確同步是直接序列擴頻（DSSS）接收機正常工作的關鍵，整個同步過程可分為捕獲和跟蹤兩個階段[1]，PN 碼的捕獲是跟蹤的前提。

PN 碼的捕獲有多種策略， 包括串行捕獲、 并行捕獲及FFT 快速捕獲等[2]。無論是哪種搜索策略都需要構造一個假設檢驗裝置，以判斷PN 碼是否完成捕獲，在假設檢驗裝置中，設定判決門限非常重要。 文獻[3]在分析判決量統計特性的基礎上，給出了在紐曼-皮爾遜準則下的門限值，但文獻[3]門限值的確定方法不具有實用性。 為了構造出具有實用價值的檢驗裝置，人們提出了多種判決門限自適應設定方法[4][5]，但是這些方法只適用于無干擾的環境。

當接收機前端存在動態干擾時, 經過中頻輸出的有用信號動態范圍變化大，傳統的固定門限法無法適應復雜的實際應用情況，必須采用自適應門限調整的恒虛警捕獲技術[8]。 干擾環境下，為提高接收機性能，在PN 碼捕獲之前插入干擾抑制濾波器，由于干擾抑制濾波器會帶來PN 碼的相關性，以及濾波器非線性相位特性會造成各頻率分量的延遲不相同，解擴后信號的能量不能很好的集中在相關峰上，會造成較大的非隨機旁瓣[6]。 在偽碼擴頻信號恒虛警自適應捕獲中估計自適應門限需要考慮這些因素， 不然會造成估計門限過高，使捕獲概率降低。

本文首先給出基本判決量的統計特性， 為了得到紐曼-皮爾遜準則下的恒虛警門限值，本文給出抑制干擾情況下等效高斯白噪聲方差的最大似然估計。 最后提出一種簡單、實用的適于抗窄帶干擾接收機的PN 碼捕獲方法， 并通過計算機仿真驗證了該方法的有效性。

1 信號模型

設直接序列擴頻系統采用BPSK 調制， 在工程實踐中通常采用平方檢波或平方累加檢波判斷信號是否捕獲。 無干擾情況下的檢測裝置如圖1 所示：

圖1 PN 碼捕獲假設檢驗裝置

圖1 中，S（t）為偽碼擴頻信號，n（t）為接收機熱噪聲，c（t）表示本地偽碼。 一般認n（t）為零均值，方差為的高斯白噪聲，Z（k）為檢測判決隨機變量，L 為非相干累積次數，VT為判決門限值。 定義兩個假設：H1：Z（k）≥VT，碼片誤差在一個碼片內；H0：Z（k）＜VT，碼片誤差大于一個碼片。

根據L 的取值情況可有：

（1）平方檢波（L＝1）檢測判決量，Z（k）＝I2（k）＋Q2（k）。

（2）平方累加檢波（L＞1）檢測判決量，

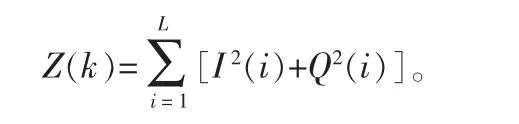
根據文獻[9]的分析，可以推導檢測判決量Z（k）的概率密度函數，以及在判決門限VT下的虛警概率Pf和檢測概率Pd。

1.1 采用平方檢波

在H0假設下，平方檢波器輸出Z（k）服從指數分布，其概率密度函數為[9]：

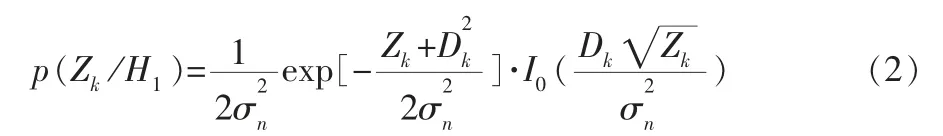
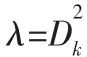
可以看出恒虛警門限由虛警概率和高斯白噪聲方差確定。

1.2 采用平方累加檢波

在H0假設下，平方累積檢波的輸出Z（k）概率密度函數為[9]：

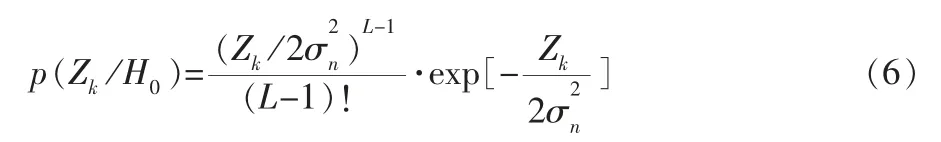
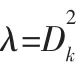
式（7）中IL－1（·）為（L－1）階修正的貝塞爾函數。可以得到捕獲信號的檢測概率和虛警概率：

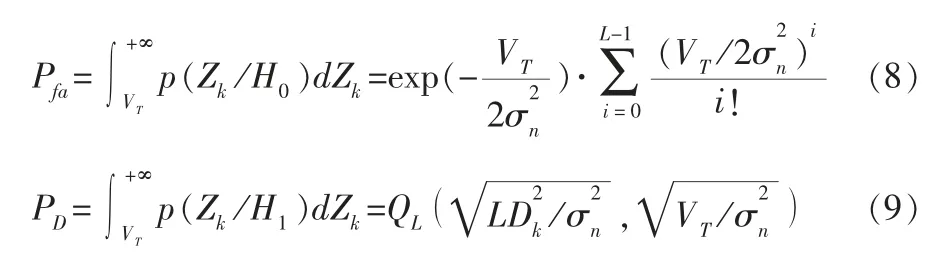
根據紐曼-皮爾遜準則，由式（8）可以得到恒虛警門限VT，可以看出恒虛警門限同樣包括高斯白噪聲方差。

2 干擾抑制濾波器對PN 碼相關性的影響

在干擾環境下，為了降低窄帶干擾對系統性能的影響，接收機需在PN 碼相關器之前插入窄帶干擾抑制濾波器。 插入濾波器必然會影響PN 碼的捕獲，文獻[6][7]中以FIR 濾波器（線性預測濾波器和線性插值濾波器）研究了窄帶干擾抑制濾波器對PN 碼捕獲的影響。 這里只給出結論（具體的推導過程可參考文獻[6]）。

線性相位插值濾波器的沖激響應為h（l），則與自適應濾波器權值之間滿足對應關系h（0）=1，h（l）=h（-l）=-wl（n），l=0，1，…，K（wl（n）為自適應濾波器收斂后得到的最優權值的估計）。 如果接收機已經實現偽碼同步，本地PN 碼與線性插值濾波器濾波后相關輸出均值和方差分別為[6]：

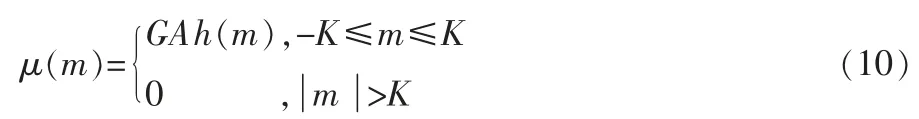
其中，A 為信號幅度，G 為一個碼周期內碼片數，2K＋1 為濾波器階數。

線性預測濾波器的沖激響應h（l）與自適應權值之間滿足對應關系h（0）=1，h（l）=-wl（n），l=0，1，…，K（wl（n）為自適應濾波器收斂后得到的最優權值的估計）。 同樣，經線性預測濾波器濾波后的一個偽碼周期的相關輸出均值和方差分別為[6]：

其中，A 為信號幅度，G 為一個碼周期內碼片數，K 為濾波器階數。

由式（10）、（12）可以看出在整個濾波器長度范圍內對于相關值會引入較大的相關旁瓣。 式（11）、（13）中等號右邊第一項為濾波器引入的“系統噪聲”，是由于干擾抑制濾波器引入了時間相關性， 使得偽隨機序列的隨機性被破壞所導致。第二項為經過濾波器之后殘留干擾的功率, 第三項表示通過濾波器之后噪聲的功率。 因此采用濾波器抑制窄帶干擾的同時，引入了PN 序列之間的相關性，進行PN 碼相關時濾波器系數范圍內會形成較高的相關峰值。

同時，當寬帶擴頻信號通過濾波器后，由于濾波器相位響應的非線性會造成各頻率分量的延遲不相同，解擴后信號的能量不能很好的集中在相關峰上， 也會使得相關旁瓣較大。

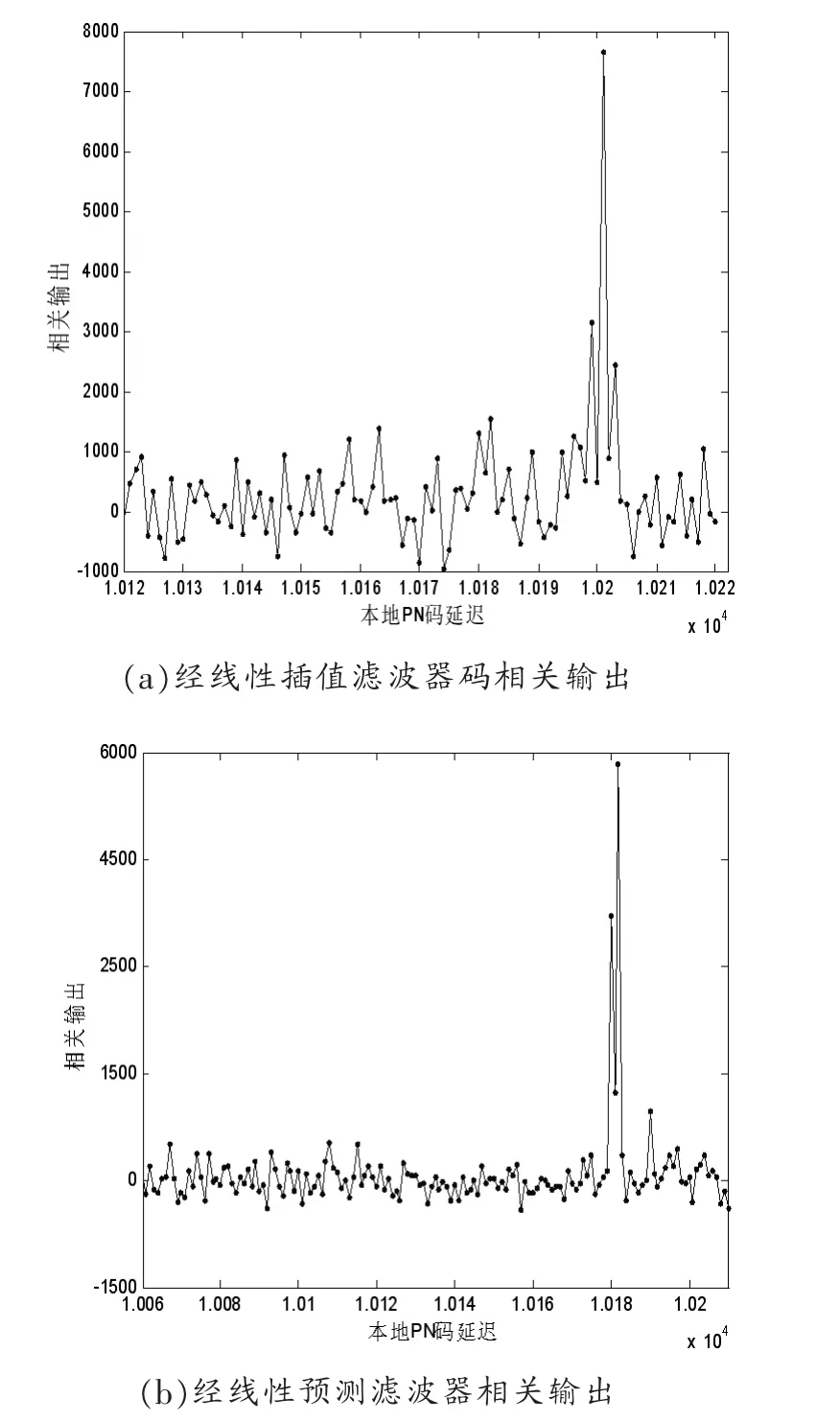
圖2 經濾波器PN 碼相關輸出

圖2（a），圖2（b）為經濾波器后PN 碼相關輸出，可以看出線性相位插值濾波器相關輸出有近乎對稱的相關旁瓣。 非線性相位預測濾波器相關值有較大的旁瓣，并且非線性相位預測濾波器的相關峰值也要比線性相位濾波要小。 估計等效噪聲方差時如果不考慮這些因素的影響，則估計的門限會偏高。

3 干擾抑制情況下噪聲功率最大似然（ML）估計

從上面的分析我們知道，兩種檢波方式下，檢測門限VT中都包含了等效高斯白噪聲功率， 而在實際應用中，是隨著環境及其它用戶干擾功率的變化而變化的，因此需要實時估計檢測門限。

觀察H0假設條件下的判決量Zk， 其概率密度函數只有是未知的，根據參數估計理論，我們可以由Zk的樣本值對進行估計[9]。 設捕獲時一次對P 個碼相位進行檢測，與之對應的有P-M 個相互獨立的判決量Zk符合H0假設，M 與濾波器抽頭數和濾波器相位特性有關， 如果采用平方累積檢波，則得到（P-M）L 個獨立同分布的觀測量Zk，這樣就可以按照一定的準則估計出，在估計出后，可以得到檢測門限的自適應估計。

我們知道，最大似然（Maximum Likelihood：ML）估計是一種最優估計[9]，因此我們采用ML 估計準則對以下兩種情況下進行估計，為方便起見令。

3.1 平方檢波（L=1）

由式（1），可推導出似然函數為：

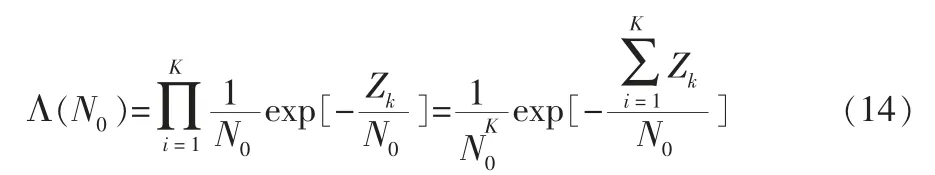
式（14）中K＝P-M，對上式取對數，得到對數似然函數

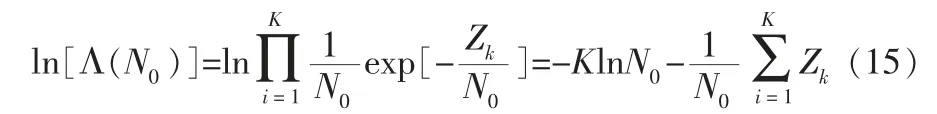
對數似然函數對N0求偏導，并取偏導值為0

解式（16），可得對N0的ML 估計

3.2 平方累加檢波（L＞1）

判決量Zk的概率密度函數為式（6），可導出似然函數為：

同理可得N0的ML 估計：

4 干擾抑制情況下PN 碼自適應捕獲裝置

由以上研究可知，對N0的ML 估計觀測樣本取（P－M）L個隨機變量，M 和濾波器抽頭數及相位特性有關， 例如窄帶干擾抑制采用線性相位雙邊插值濾波器，若相關輸出最大值的位置為j，則應去掉相關輸出［Zj－M，…，Zj，…，Zj＋M］。 令U=［Zj－M，…，Zj，…，Zj＋M］。 對于IIR 濾波器M 必須根據實際情況通過仿真確定。

基于以上分析得到抑制窄帶干擾接收機的偽碼自適應捕獲裝置，如圖3 所示：

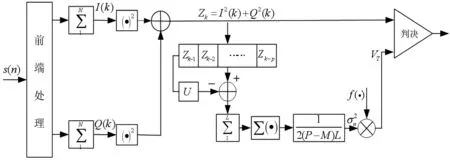
圖3 窄帶干擾抑制接收機的自適應偽碼捕獲

圖中f（·）為求虛警概率的函數，可由式（3）或式（8）確定。

5 數值仿真與分析

仿真條件為：輸入信號是20MHz 帶寬擴頻信號s（t）=c（t）·cos（2πfct），c（t）是偽隨機碼；j（t）=Acos（2πfjt），幅度A 可調；產生接收機帶寬內高斯白噪聲；采樣頻率fs為60MHz。 窄帶干擾抑制采用線性相位插值濾波器，為了驗證自適應捕獲裝置的有效性。

從圖4 為L=1 時噪聲功率的設定值與本文方法噪聲功率的估計值之間的比較，圖5 為在不同虛警概率下檢測概率和理論值的比較。 從圖4 和圖5 的仿真結果可以看出，采用估計門限構造的PN 碼捕獲裝置性能與前面理論分析結果非常吻合,這說明了本文提出的方法是有效性的。

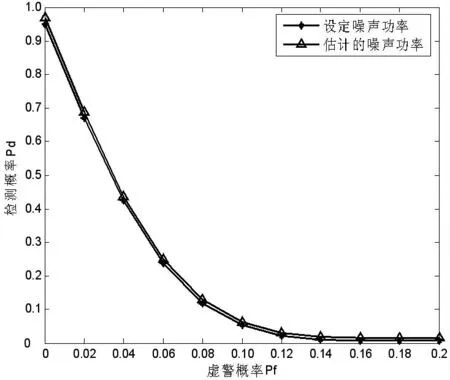
圖4 L=1 噪聲功率估計值

6 結束語

圖5 L=1 檢測概率仿真結果

本文提出一種直接序列擴頻接收機抑制窄帶干擾情況下，PN 碼自適應捕獲方法，在分析檢測量統計特性及干擾抑制濾波器對PN 碼相關性影響的基礎上， 采用最大似然估計得到等效高斯白噪聲方差。 設計了在紐曼-皮爾遜準則下的PN 碼自適應捕獲裝置。 通過計算機仿真驗證了該方法的有效性。 本文方法簡單，很適合工程應用。S

［1］Elliott D.Kaplan. GPS 原理與應用[M].邱致和，王萬義，譯.北京：電子工業出版社，2002.

［2］孫李,張其善.GPS 數字接收機中C/A 碼搜索算法與實現[J].北京航空航天大學學報，1998,24（5）：506-509.

［3］A J Viterbi.CDMA Principles of Spread Spectrum Communication[M].US： Addison Wesley Pub,1995.

［4］薛巍,向敬成,周治中.一種PN 碼捕獲的門限自適應估計方法[J].電子學報,2003,31（12）：1870-1873.

［5］R D Gaudenzi.Direct Spread Spectrum Receiver Including Code Acquisiton and Detection Using an Antoadaptive Threshold [P].US Patent：5,818,868,1998.

［6］李崢嶸,桑懷勝,王飛雪,等.擴頻系統中自適應窄帶干擾抑制濾波器對PN 碼捕獲性能的影響[J].電子學報,2002,30（12）： 1768-1771.

［7］張春海.DS-CDMA 時域抗窄帶干擾接收機性能分析[J].航天電子對抗,2005,21（5）：50-64.

［8］王世練,高凱,李紀，等.抗窄帶干擾寬帶中頻數字接收機的設計與實現[J].電路與系統學報,2004,9（2）：138-141.

［9］沈鳳麟,葉中付,錢玉美.信號統計分析與處理[M].合肥： 中國科學技術大學出版社,2001.