淺談數控機床幾何誤差及補償方法的研究
鐘培榮
(肇慶科技職業技術學院 廣東 肇慶 526100)
數控機床的加工精度決定零件的精度,而數控機床零部件之間的配合影響著加工精度,于是,就出現了數控機床幾何誤差。 數控機床幾何誤差一般來自于數控機床制造過程的缺陷、數控機術內部零件與零件之間的公差配合以及加工溫度變化帶來的機械熱變形,機床加工溫度帶來的機械熱變形主要來源于齒輪與齒輪之間的摩擦阻力,加工通電過程中的電線電阻發熱,發動機運轉產生的熱量等,這些都可以通過改善數控機床的內部環境得到解決。 數控機床的幾何誤差很難通過改善機床的內部環境就能解決,唯有通過參數測量出誤差值,然后人為地設置一個反方向的誤差,彌補數控機床的機械誤差,從而提高數控機床的加工精度.因此,誤差補償技術作為一種提高機床精度的有效和經濟的手段得到了廣泛的重視。
1 誤差補償原理概述
數控機床的誤差補償原理,就是人為地設置一個與數控機床幾何誤差反方向的誤差, 彌補數控機床的機械誤差,從而提高數控機床的加工精度的技術方法。 近年來,機械在各行各業的廣泛應用,使得數控機床的加工應用技術得到飛速發展,因此,數控機床的誤差補償技術,得到廣泛關注和重視。 數控機床誤差動態綜合補償已列入國家科技重大專項“高檔數控機床與基礎制造裝備”。
2 幾何誤差補償方法
隨著數控機床的發展, 誤差補償技術按照其發展歷史,可以劃分為三個發展階段:
(1)機械式靜態補償法
機械式靜態補償法,又叫硬件誤差補償法。 數控機床在生產應用階段,對數控機床進行調試,得出誤差值,通過對數控機床更換零部件,改善數控機床的內部構造,從而減小數控機床的誤差, 這種方法不能提高數控機床的柔性誤差,收到的效果不明顯, 不能滿足數控機床加工的產生的誤差問題。所以,未得到廣泛應用和普遍關注。這個最初的數控機床誤差補償技術,漸漸地被實時補償法替代。
(2)實時補償法
實時誤差補償法是通過安裝一個與數控機床數據相聯接的機床輔助裝置,把數控機床的各項參數,包括溫度和機床位置等,輸入到輔助裝置中,輔助裝置的機床實體建模對參數進行對比分析,得出機床誤差值,然后采用誤差補償,而提高數控機床加工精度。 實時補償法在數控機床中的應用較實用和廣泛,可以補償多種類型的誤差,例如定位誤差,定形誤差,溫度誤差等,并且,針對不同的數控機床,有多種不同的機床誤差模型,這樣,大大提高了實時補償法應用的靈活性。 提高補償的實時性、準確性、有效性和簡便性是誤差補償實施技術研究的關鍵。
數控機床實位誤差測量方法最常用的是激光技術,通過在數控機床上安裝一個激光測量儀器,激光測量儀器把機床和被加工零件的體積分割成相等區間的測量點,然后將測量這些點的數據通過誤差插補的方法獲得整個機床的誤差函數。 選用不同種類的光學儀器,可以測量出數控機床多種不同的誤差值。
(3)軟件補償法
軟件誤差補償法,是在數控機床中建立一個閉環的模型軟件系統,在加工過程中,將實時的參數傳輸給模型軟件系統,軟件系統進行分析,得出誤差值,再將調整結果反饋給數控機床系統,進行加工調整,這屬于動態補償方法,一邊零件加工,一邊進行誤差補償。 與其它的誤差補償方法相比較,軟件誤差補償法能使數控高精加工在實際加工過程中始終得以實現。 軟件補償法的特點在于不需要改動數控機床的內部結構,數控機床只需連接一臺計算機,數控機床與軟件模型系統實時參數傳輸,完成和誤差補償的目的,達到數控機床高精加工的要求。 軟件誤差補償克服了數控機床制造時所帶來的硬件缺陷,數控機床與軟件系統的配合使用,是誤差補償的一種理想的補償方式。 軟件補償技術發展到今天,大致可分為兩種方法:(1)反向間隙誤差補償;(2)由螺距累積誤差等引起的常值系統性定位誤差的補償。
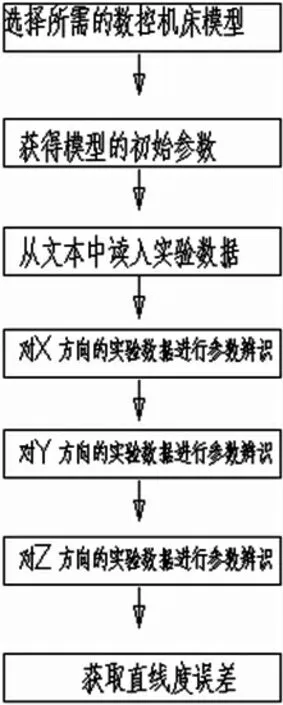
圖1 參數辨識流程圖
在圖1 中,說明了參數辨識的程序框圖,在進行參數辨識之前,我們首先必須確定了數控機床運動模型和獲得初始參數。
3 誤差補償的實現
誤差補償的實現,是通過軟件系統接收來自數控機床的實時參數,然后對原先的數控指令進行修改,控制加工刀庫中正在加工零件的刀具不斷修改加工路徑,使刀具去到準確的加工點上,從而實現誤差的補償,達到高精度加工。 本文采用數控機床加工點的絕對坐標值減去誤差值,得到數控機床加工點的真實值,從而控制刀具路徑達到誤差補償。
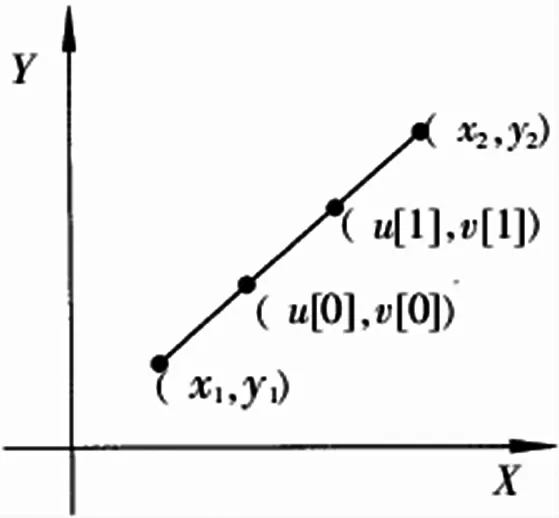
圖2 直線的分段
誤差補償的關鍵是求出刀具實際加工路徑與理想狀態下的加工路徑之間的不同,即是要得出數控機床刀具加工運動到任意點的誤差值。 要得到加工刀具起點和終點的各項誤差,機床參數誤差辨識可以幫忙解決以上各種難題。 在本文中,要重點提出的是,機床誤差辨識是建立在數控機床的絕對坐標系中的誤差值,而數控機床加工時,刀具加工路徑的坐標值是機床相對坐標系中進行的,如果要實行機床誤差辨識,必須要進行數控機床絕對坐標值與相對坐標值之間的互相轉化。
圖2,直線的分段,首先通過X=X2-X1,Y=Y2-Y1,Z=Z2-Z1,得出X、Y、Z 三個方向中位移最大值a,然后,用位移最大值a除以每段線段長度的平均值b,將得出的數值進行四舍五入,得到一個整數n,然后將n+1,就是所求的線段數。 接著,先用公式求出某方向上各段線段的終點坐標, 再由直線方程y=kx+b,得到其它兩個方向的坐標值(以x y 平面x 方向位移為例)。

圖3 圓弧的分段
U[i]=(i+1)*m/(n+1)
V[i]=U[i]*(y2-y1)/(x2-x1)
圖3,圓弧的分段,先根據圓弧的半徑R 和圓心角θ 求出圓弧的長度,然后與采取同樣的方法。 用圓弧的長度a 去除以分段步長d,得到的值取整得到的整數n 加上1,就是所要分的段數對于各段終點坐標的x,y,z 值,采用坐標變換的方法先在以圓弧圓心O 為原點的坐標系中用R、a 求出末點的坐標值,然后再變換到工件坐標系中。 此時,分段后的數控程序不能再用I,J,K 來表示原點位置了,而統一使用半徑R 來實現。
U[i]=R+X0
V[i]=R+Y0
[1]林奕鴻.機床數控技術及其應用[M].機械工業出版社,1996.
[2]王秀山,陳英.國外數控機床誤差建模與補償技術研究的歷史及現狀分析[J].科技情報開發與經濟,2010,20(31).
[3]李書和.數控機床誤差補償的研究[D].天津:天津大學,1996.
[4]張虎,周小飛,等.數控機床精度強化方法研究[J].機械與電子,2000.

