均勻分布的區間估計方法及應用
徐曉嶺,朱靈芝
(1.上海對外貿易學院 商務信息學院,上海 200234;2上海師范大學 數理學院,上海 200234)
均勻分布的區間估計方法及應用
徐曉嶺1,朱靈芝2
(1.上海對外貿易學院 商務信息學院,上海 200234;2上海師范大學 數理學院,上海 200234)
文章給出了均勻分布在全樣本場合下參數的三種區間估計方法,通過大量Monte-Carlo模擬考察了各種區間估計方法的精度,并通過實例說明了這些區間估計方法的應用。
均勻分布;全樣本;區間估計;MonteCarlo模擬
設總體X服從區間[θ1,θ2]上的均勻分布,記為X~U[θ1,θ2],X1,X2,…,Xn為來自X的一個樣本,可以證明:θ1,θ2的極大似然估計分別是:=X(1),=X(n),其中X(1),X(n)分別為最小和最大次序統計量。
1 全樣本場合下參數θ1,θ2的區間估計

設 X1,X2,…,Xn為來自總體X~U[θ1,θ2]的容量為n的一個簡單隨機樣本,X(1)≤X(2)≤…≤X(n)為其次序統計量。下面通過三種方法來求參數θ1,θ2的置信水平1-α的區間估計。



為考察全樣本場合下上述三種區間估計方法的優劣,給定樣本容量n=10(5)30,參數真值θ1=2,θ2=5,置信水平為1-α=0.95,通過1000次Monte-Carlo模擬得到參數θ1,θ2的區間估計的平均下限、平均上限、平均區間長度和包含參數真值的個數,結果列于表1、表2、可以看到,從平均區間長度來看,方法一較好。
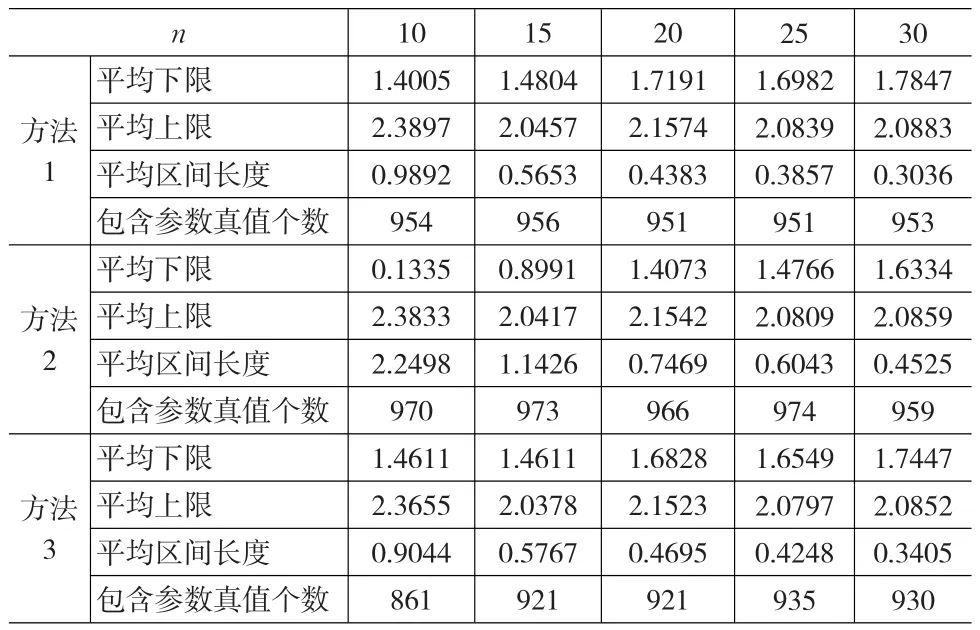
表1 全樣本場合下參數θ1的區間估計的模擬結果
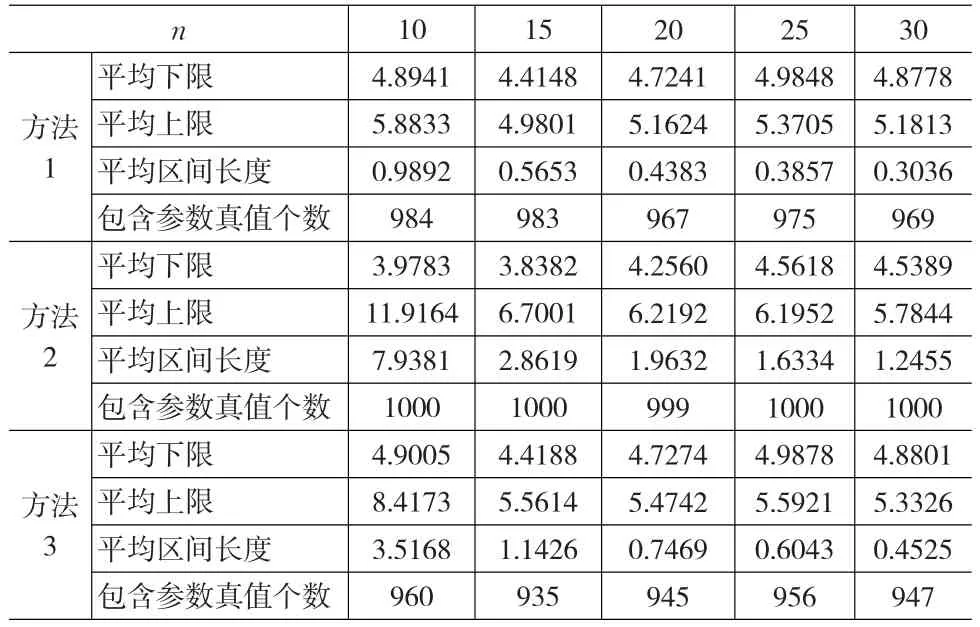
表2 全樣本場合下參數θ2的區間估計的模擬結果
例:給定樣本容量為n=20,參數真值為θ1=6,θ2=8,通過Monte-Carlo模擬產生一組服從均勻分布的隨機樣本:7.5048,6.9629,6.8739,7.1731,7.1797,7.3868,7.2132,7.1207,7.9245,6.4690,6.6101,6.3016,7.0824,6.7201,6.3803,6.7344,7.8960,7.3130,7.5301,6.0425.
在全樣本場合下,利用本文三種區間估計方法可得:參數θ1的置信水平為95%的區間估計分別為:方法1[5.7210,6.0425],方法 2[5.4924,6.0401],方法 3[5.6944,6.0387];參數θ2的置信水平為95%的區間估計分別為:方法1[7.9245,8.2459],方法 2[7.5813,9.0208],方法3[7.9269,8.4745],其中方法一的區間長度最短。
2 結論
在全樣本場合下,從平均區間長度來看,本文所給出的均勻分布的參數θ1,θ2的三種區間估計方法中,方法一精度最高。
[1]E.L.Lehmann.Elements of Large-sample Theory[M].New York:Spring er,2010.
[2]王秀麗.均勻分布參數的最短置信區間[J].數學的實踐與認識,2008,(9).
[3]顧蓓青,徐曉嶺.關于均勻分布統計分析的一些思考[J].統計與信息論壇,2010,(12).
O212
A
1002-6487(2012)24-0023-03
國家自然科學基金資助項目(11141002);上海對外貿易學院085重點學科專業建設項目;上海市星系與宇宙學半解析研究重點實驗室項目(SKLA1101)
徐曉嶺(1965-),男,江蘇宜興人,博士,教授,研究方向:可靠性統計。
朱靈芝(1985-),女,湖北枝江人,碩士研究生,研究方向:可靠性統計。
(責任編輯/亦 民)

