Clifford代數Clp,q的冪等元
張桂穎, 紀云龍, 李武明
0 引 言
Clifford代數Clp,q是由p+q維 Minkowski空間Rp,q生成的一類2p+q維的實結合代數,在數學和物理中有諸多應用[1-3]。在對 Clp,q理論的研究中,人們注意到可除的Clp,q只有R≌Cl0,0,C≌Cl0,1,H≌Cl0,23種。故此,人們非常關注非可除的Clp,q的研究。文中的主要結果有:
1)Clp,q非可除代數的充分必 要條件是Clp,q有非平凡冪等元;
2)若Clp,q的中心子代數Cen(Clp,q)有非平凡冪等元,則Clp,q有雙環結構。
1 Clp,q有非平凡冪等元的等價命題
Clifford代數Clp,q的一組基[1-3]為:
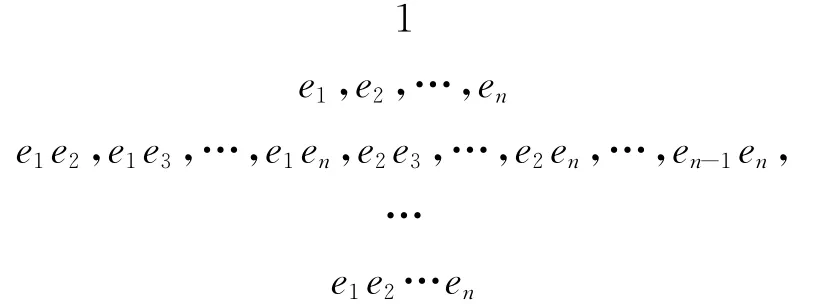
且滿足
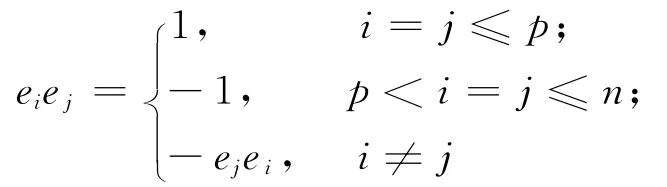
定義1[1]設A為域F上代數,利用A的加法運算與乘法運算,在
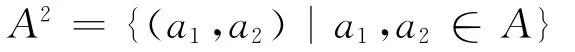
上定義加法運算與乘法運算為:
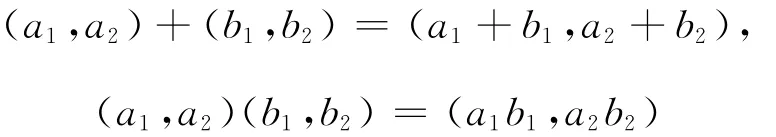
則A2構成環,稱其為A的雙環,記為2A。
下面我們把Clp,q中滿足u2=1,u≠±1的元素u稱為Clp,q的非平凡自逆元。
定理1 設Clp,q是由p+q維 Minkowski空間Rp,q生成的Clifford代數,則有如下等價命題。
1)Clp,q有非平凡零因子;
2)Clp,q有非平凡冪等元;
3)Clp,q有非平凡自逆元;
4)Clp,q有子代數同構于雙環2R。
證明
1)?3),Clp,q有非平凡零因子,即Clp,q是非可除的[4-7],可知p>0或q>2。當p>0時,Clp,q有非平凡自逆元e1,命題成立。當p=0時,必有q>2,Clp,q有3次單位向量e123為其非平凡自逆元。
3)?2),設u是Clp,q的一個非平凡自逆元,令
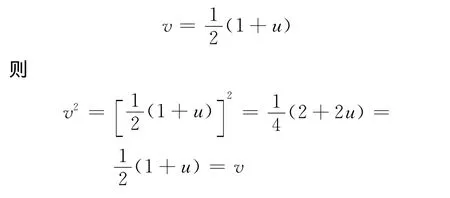
即v是Clp,q的非平凡冪等元。
2)?1),設v是Clp,q的非平凡冪等元[8],則存在非零元1-v,使得v(1-v)=0,即Clp,q有非平凡零因子。
3)?4),若Clp,q有非平凡的自逆元u,u2=1,即u為Clp,q的一個雙曲虛單位,從而Clp,q有子代數{a+bu|a,b∈R}≌H≌2R。
4)?3),若Clp,q有子代數與雙環2R 同構,即與雙曲數 H={a+bj|a,b∈R}同構,從而Clp,q有雙曲虛單位j,即為Clp,q的非平凡自逆元。
2 冪等元與Clp,q的結構
定理2 若Clp,q的中心 Cen(Clp,q)有非平凡冪等元,則 Cen(Clp,q)≌2R,且
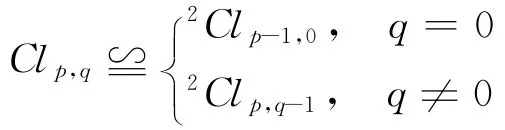
即 Cen(Clp,q)與Clp,q均有雙環結構。
證明 由于Clp,q的中心子代數只可能同構于R,H 與C,而R與C中均無非平凡冪等元。故 Cen(Clp,q)有非平凡冪等元時,必有
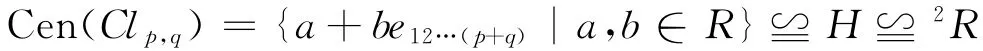
下證
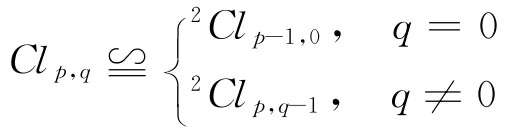
1)任取a∈Clp,q-1,b∈Cen(Clp,q)有ab=ba;
2)Clp,q=Clp,q-1Cen(Clp,q);
3)dimClp,q=2p+q=2p+q-1·2=dimClp,q-1dimCen(Clp,q)故有
當q≠0時,有
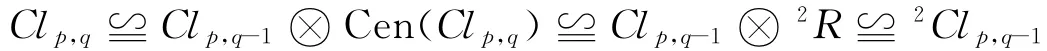
同樣可證,當q=0時,有
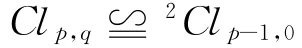
推論1 若e
12…(p+q)
為自逆元,且
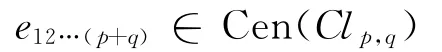
則
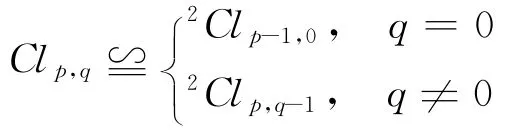
[1] Lounesto P.Clifford algebra and spinord[M].Cambridge:Cambridge University Press,2001.
[2] 李武明.Clifford代數與 Minkowski空間的性質[J].吉林大學學報:理學版,2000,10(4):13-16.
[3] 李武明.Clifford代數與n維 Minkowski空間的性質[J].吉林大學學報:理學版,2003,13(4):29-32.
[4] 李武明,張慶成.四維雙曲復空間與Lorentz群[J].東北師范大學學報:自然科學版,2005,37(2):15-17.
[5] 曹文勝.四維Clifford代數的相似與合相似[J].數學物理學報,2010,30A(2):531-541.
[6] 吳亞波.Clifford代數中的雙曲相位變換群及其在四維相對論時空中的應用[J].物理學報,2005(11):11-16.
[7] 李武明,張雪峰.時空平面的Clifford代數與Abel復數系統[J].吉林大學學報:理學版,2007,45(5):748-752.
[8] 紀云龍,宮莉.關于廣義冪等矩陣Schur補的函數的一個性質[J].長春工業大學學報:自然科學版,2007,28(3):213-216.

