多品種小批量元器件的統計過程控制
康 蜜,趙金丹
(1.中國電子科技集團公司第47研究所,沈陽 110032;2. 中國聯通(集團)有限公司遼寧省分公司,沈陽 110031)
1 引言
SPC原理是根據數理統計分析理論,對連續采集多批的工藝參數數據進行定量統計分析,對工藝過程是否處于統計受控狀態作出定量結論,當出現工藝能力下降,工藝過程失控或有失控傾向時,立即發出警報,及時提示生產方查找原因,采取糾正措施,使工藝過程始終處于統計受控狀態,為生產高質量水平的產品提供保障。在國際上SPC技術早已在大規模生產的傳統工業中得到廣泛應用,并且由于低投入、高產出的技術特點產生過巨大的經濟效益,雖然電子工業尤其是元器件生產中存在很多不同于傳統工業的特殊問題,但從20世紀80年代中期開始SPC技術也在元器件生產中得到普遍應用,使產品在統計受控的高水平生產線上生產,從而具有較高的內在質量和可靠性。SPC技術通常應用于大規模生產,擁有充足的數據源,為數據分析提供足夠樣本,為分析工藝過程是否處于統計受控做出科學判斷。但在我國很多元器件生產企業都存在多品種、小批量的訂貨情況,如何對多品種、小批量的生產過程進行統計過程控制,如何解決小批量生產數據量不足的問題,如何使小批量產品具有像大批量產品同樣的質量和可靠性,以及如何根據用戶要求提供元器件生產過程中的質量波動數據,成為要解決的問題。
2 SPC技術概述和常規控制圖
2.1 SPC技術概述
工業生產中,即使宏觀的工藝條件未有變化,但是影響產品質量水平的5MIE因素絕對保持不變是不可能的,即表征工藝結果的工藝參數是存在波動的。從數理統計角度分析,波動原因分為隨機原因和異常原因。
隨機原因不可避免,始終存在,這類原因對工藝參數的影響具有偶然性、不確定性,但總體遵循一定統計規律。
異常原因只有在其存在時才會對產品生產過程起作用。實際生產中,可以通過對表征工藝結果的工藝參數數據進行定量分析,來判斷工藝過程是否出現異常,是否存在影響工藝結果的異常原因。若工藝過程只存在隨機原因,不存在異常原因,表征工藝結果的工藝參數數據服從同一種分布,則稱工藝過程處于統計受控狀態,這就是對產品生產制造過程引入統計過程控制SPC(Statistical Process Control)的過程。
SPC原理是根據數理統計分析理論,對連續采集多批的工藝參數數據進行定量統計分析,對工藝過程是否處于統計受控狀態作出定量結論,當出現工藝能力下降、工藝過程失控或有失控傾向時,立即發出警報,及時提示生產方查找原因,采取糾正措施,使工藝過程始終處于統計受控狀態。由此可見SPC技術具有事前預防的作用。
20世紀80年代以前,國際上的元器件生產廠商主要通過檢驗方式(包括產品篩選及可靠性試驗等)保證產品質量,很明顯這是一種事后預防的方式。根據元器件失效率隨時間變化的“浴盆曲線”顯示,篩選試驗只能剔除早期失效的產品,不能降低偶然失效期間的失效率,因此通過篩選和檢驗試驗只能提高產品的使用可靠性,并不能真正提升產品的內在質量和可靠性。所以,產品內在質量和可靠性并不是檢驗出來的,而是設計、制造和管理出來的。
SPC技術是通過對工藝過程進行統計過程控制,使得工藝過程始終處于穩定受控狀態,將質量建立在產品內部,真正提升產品質量水平和可靠性。我國在1997年頒布了GJB3014-97《電子元器件統計過程控制體系》國家標準,使得SPC技術在電子元器件行業得到廣泛推廣和應用。
2.2 SPC技術評價流程
根據GJB3014-97對生產過程實施SPC,需要制定SPC大綱,對生產過程各個方面均要做出規劃,技術方面包括確定評價對象、數據采集以及控制圖選用三方面。
確定評價對象是指確定關鍵工序,并且確定關鍵工序的關鍵工藝參數。所選定的工藝參數必須能夠確實表征工序的運行狀態,可以是一個或者多個工藝參數。由于SPC是通過分析參數數據的起伏變化定量判斷工藝過程是否處于統計受控,所以要求能夠對所選參數進行定量測試取得具體數值,并且測試結果要達到一定的準確度和精密度。
SPC分析的基礎是數據,所以對所采集的數據也有一定要求。在分析用控制圖階段,需要積累25批數據(至少20批)。在控制用控制圖階段對采集的每批數據都應進行統計受控狀態的分析,對于計量值控制圖每批數據個數不應少于5個。如果某些工序只能采集一個數據,則應選用單值-移動極差控制圖。對于計數值控制圖,所采集每批數據的個數應該足夠多,控制圖才能正確反映工藝狀態,數據采集的方案可以根據生產實際情況確定,比如小容量、高頻次數據采集方案或者大容量、低頻次數據采集方案。
數據采集之后,就需要選用控制圖分析數據,根據數據特點選擇合適的控制圖才能對采集數據做出正確分析,才能對工藝過程是否穩定受控做出正確判斷。
2.3 常規控制圖
控制圖是在具有控制限的坐標系中用折線表示工藝參數隨批次的變化情況,不同的控制圖表征的工藝參數特征值不同,繪制控制圖的作用是依據數理統計原理,從圖上數據點的起伏變化情況,分析數據點和上下控制限的相互關系,從而判斷工藝過程是否處于統計受控狀態。常規控制圖根據工藝參數的不同屬性分為計量值控制圖和計數值控制圖。計量值控制圖包括均值-標準偏差控制圖、均值-極差控制圖、單值-移動極差控制圖等,計數值控制圖包括計件值控制圖(不合格品率控制圖和不合格品數控制圖)、計點值控制圖(單位缺陷數控制圖和缺陷數控制圖)。
應用常規控制圖的前提是工藝參數滿足一定條件,比如計量值控制圖要求被分析的數據滿足IIND條件(Independently & Identically Normally Distributed),即相互獨立、同分布條件,計數值控制圖根據不同控制圖,要求所選擇數據滿足二項分布或泊松分布,所以應根據工藝參數的分布特點選擇合適類型的控制圖。在元器件生產中,一部分工藝參數滿足IIND條件,比如內引線鍵合拉力,這類參數可以應用常規控制圖分析工藝狀態,但也有相當一部分工藝參數不滿足IIND條件,常規控制圖并不適用此種參數,所以需要使用特殊的SPC控制模塊,比如嵌套控制圖、回歸控制圖等。
3 多品種小批量元器件生產存在的統計問題
3.1 數據量不足
統計質量控制和評價技術流程中工藝受控狀態定量分析是通過繪制控制圖完成的,控制圖的作用是從圖上數據點的起伏變化情況,以及數據點和上下控制限的相互關系,根據數理統計原理判斷工藝過程是否處于統計受控。為保證控制圖正常運作,反應出關于生產過程統計受控狀態的正確信息,繪制控制圖時對所采集的數據有一定要求,包括數據批數及每批所含數據量。
21世紀以來我國航空工業和武器裝備行業快速發展,由于產品結構日趨復雜和行業的特殊性,所需元器件的品種及數量飛速增長,對于元器件的需求日趨個體化和多樣化,使得元器件生產企業大批量生產過程的比例不斷減少,多品種小批量正在成為主要的生產方式。此種方式的主要特點是品種多、批量小、工藝參數多樣化及設備調整頻繁等,因此給生產方增加了管理和組織難度,影響產品質量的因素也更加復雜。統計過程控制作為過程質量控制的關鍵技術,主要面向大批量生產,以充足的數據為基礎,對同一產品的某一特征值進行控制。而多品種小批量生產方式缺少足夠的樣本數據,所以傳統的統計過程控制方法不能直接有效使用,如何保證此種情況下產品的質量水平,成為要解決的問題。
3.2 工藝參數嵌套特性
半導體元器件生產中經常出現工藝參數嵌套性問題。在微電路生產中與晶片加工有關的工藝參數往往呈現嵌套特點,比如氧化、注入工序等。每一片晶片上的工藝參數(如氧化層厚度等)均服從均值為μd、標準偏差為σd的正態分布,此為一階嵌套。而同一批次加工中不同位置的晶片之間,每片晶片上的μd又服從另一個均值為μW、標準偏差為σW的正態分布。連續加工多批晶片之間,均值μW又服從另一個均值為μb、標準偏差為σb的正態分布,這就是多階嵌套。由于工藝參數的嵌套性,這類參數不滿足IIND條件,因此不能使用常規控制圖對采集數據進行定量分析,如果使用常規控制圖會出現統計信息錯誤,對工序的受控狀態做出錯誤的判斷。
4 解決方法
由于多品種小批量的元器件生產存在數據量不足和加工工藝過程中多有工藝參數嵌套性的問題,采用常規控制圖分析有可能對工藝過程的受控狀態進行誤判,所以此種情況下對工藝過程進行統計過程控制應用特殊的SPC模塊進行數據分析。對于半導體元器件生產中出現的工藝參數嵌套性問題,解決方法是采用基于嵌套統計原理的嵌套控制圖;對于多品種小批量產品數據量不足的問題,解決方法是回歸,即將小批量轉化為大批量,將短制程轉化為長制程。
品種雖然呈現多樣化,但加工過程日趨集中化和標準化,生產過程中相同或相似的加工過程比例不斷提高,所以對型號不同但結構相似的元器件采用共同數據統計的方法實施SPC控制。影響工藝穩定的關鍵參數包括操作人員、加工設備、加工工藝和原材料。雖然產品型號不同,但實際生產過程中,很多工序的加工條件相同,比如鍵合工藝,不論產品本身可實現的功能有多不同,產品均在同樣的鍵合設備上鍵合,由同一批技術人員操作,采用相同規格、材質及相同原材料來源的鍵合絲鍵合,芯片的焊盤加工工藝也相同等,這時可認為此道工序加工出的不同產品的工藝參數服從同一種分布。此時,不同型號產品的鍵合數據可以共享,共同構成SPC的數據源。但無論哪種影響工藝穩定的關鍵參數發生變化,都要對參數重新進行評估,看其是否可以同一化。比如鍵合絲直徑改變,相應的鍵合設備參數也需要調整,此時不能將不同直徑的鍵合絲拉力數據共享,而需要向前尋找相同加工條件的鍵合數據,但不同數據之間時間間隔過大也是不合適的。
如果某個關鍵工序統計數據較少,不能提供足夠的樣品用于測試,即使采用數據共享方法也得不到足夠的數據量,這時就要分析是否可以將控制點前推。雖然數據點外推風險較大且理論支持不夠,但可以解決本道工序不能提供測試數據或者測試數據量不足的情況。控制點外推的前提是工序加工條件相似,如果不是,要考慮其他方法。
5 嵌套回歸控制圖的應用
為保證有限批次數據的計算結果能代表母體數據的特征值,在確定控制限時需要積累25批數據(至少20批)。對計量值控制圖,即使母體不是正態分布,只要每批數據不少于5個,每批數據的特征值仍近似為正態分布。因此,計量值控制圖中每批數據個數不應少于5個。此處不進行嵌套和回歸方面數學原理的論述,只利用已知理論演示嵌套回歸統一處理數據的流程。以元器件生產中廣泛采用的電鍍工序為例,對鍍層厚度參數進行嵌套回歸的統一化處理。采用25批次的樣品,每批樣品采集10個數據組成SPC分析的一批數據,如表1所示。

表1 SPC分析數據
(1)處理數據:回歸。
計算鍍層A鍍層厚度的均值和標準偏差:
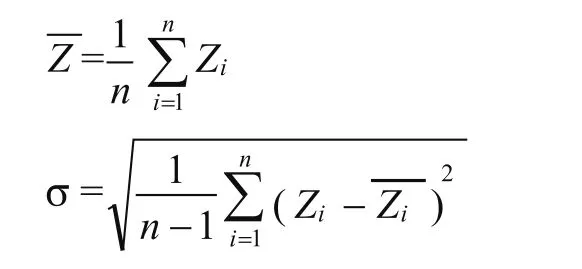
計算鍍層A鍍層厚度的回歸值:
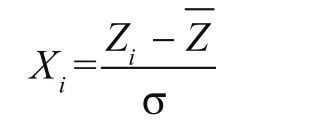
同理計算鍍層B的鍍層厚度回歸值。

(3)計算每組鍍層厚度回歸樣本的標準偏差Si。
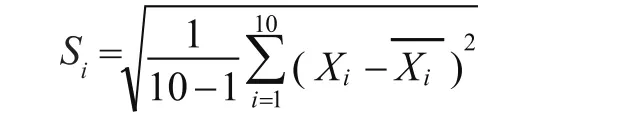
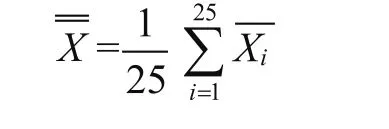
(5)計算全部鍍層厚度回歸分組樣本標準偏差和組內標準偏差。
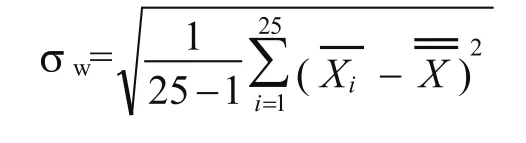
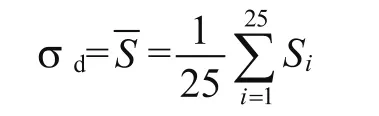
S控制圖:
其中a、b可通過計算得出。
通過專業SPC軟件繪制控制圖可知,若對鍍層厚度參數采用傳統的均值-極差控制圖,得到的控制圖出現很多數據點超出控制限的情況;若考慮參數的嵌套特點采用回歸嵌套控制圖,可以確認工藝處于穩定受控狀態。由此可知,采用錯誤的控制圖分析數據有可能對工藝受控狀態進行誤判,從而給生產方帶來排查工藝失控因素的困擾。
6 結論
在半導體元器件生產過程中經常出現工藝參數嵌套性的問題,選擇適合嵌套特性的特殊SPC控制模塊對采集數據進行定量分析,可以對工藝過程的受控狀態進行正確判斷,為保持工藝穩定、提高工藝質量提供保障。
[1]賈新章,李京苑.統計過程控制與評價[M].北京:電子工業出版社,2004.
[2]劉建.小批次元器件SPC過程中嵌套回歸方法研究.[J].電子質量,2011(10).

