三維隨行電纜簡化模型有限元建模與模態實驗

肖 闖 殷智宏

湖南大學汽車車身先進設計制造國家重點實驗室，長沙，410082

0 引言

纜索是電梯系統中非常重要的部件，典型的電梯用纜索可分為兩種形式：一種是承載纜索，主要承受電梯轎廂和配重的載荷；另一種為非承載電纜索，包括隨行電纜和補償電纜。前者用于提供轎廂電源和控制信號，后者作為電梯配重使用。隨行電纜的一端固定在電梯間的墻壁上，另一端隨著電梯轎廂上下運動。隨行電纜的截面形式通常為圓形或矩形。

隨著建筑物高度的增加，電梯系統的纜索長度也隨之增加，可達數百米。電梯上下運動過程中伴隨著振動而造成電纜自身打結或由于振幅過大而撞擊到電梯間的墻壁，非常危險。商業用途建筑物的設計原則是最大化租用或使用面積，因此，電梯間的面積在設計中所占的比例越來越小，隨行電纜的允許活動空間也會相應地減小。因此，超長隨行電纜的動力學分析越來越受到電梯制造商和設計者的關注。對于繩索動力學特性的研究，國外科研工作者曾對小張力的繩索進行了動力學分析［1］。Howell［2］采用顯示有限差分計算和隱式有限差分計算方法分析了無張力或低張力的繩索的動力學特性；Sun等［3］在廣義坐標下建立了海底三維電纜的動力學方程，研究了低張力的繩索特性。在過去的幾十年間，對低張力電纜的研究僅限于理論的模型推導，并沒有實驗研究。通常人們通過平面模型來研究隨行電纜的動力學特性［4］。但實際上，隨行電纜的振動來源于水平、垂直和側向三個方向的激勵，而且由于建筑物本身的搖擺，會造成繩索兩端同時被激發振動，其動力學響應更加復雜［5］。所以二維的平面模型并不能真正反映隨行電纜的動力學特性。

本文以三菱電梯系統的隨行電纜（矩形截面）為例研究其動態特性；利用細長鋼帶模擬實際電梯系統中的隨行電纜；基于模態測試手段［6－7］，獲得模態參數；采用三維有限元模型研究隨行電纜的動力學特性，并通過實際模態實驗進行驗證。

1 模態實驗準備

為了保證實驗的準確性，同時提高實驗數據的質量，實驗初期首先確定合理的邊界條件，然后利用梁單元建立細長鋼帶系統粗略有限元模型，計算得到固有頻率和振型，作為模態測試的指導。

1.1 確定邊界條件

實驗室中的桁架結構作為細長鋼帶模擬隨行電纜的邊界條件，如圖1所示。若直接將細長鋼帶兩端完全固定在桁架上，由于系統的剛度較大，鋼帶將與桁架的振動耦合在一起，從而造成實驗結果不可靠。對于上述問題，采用長為0.01m的鋼絲焊接在鋼帶兩端，并將鋼絲的另一端利用夾具固定在桁架上。這種兩端固定的約束形式不僅克服了振動耦合的問題，減小了系統的剛度，而且便于在低頻范圍內得到平面內和平面外的模態。

圖1 實驗設置及邊界條件

1.2 梁單元有限元模型預測

對于電梯隨行電纜而言，其低階頻率更為重要，所以選定的測量范圍為0～25Hz。梁單元有限元模型的仿真結果顯示，在此頻帶中有15階模態振型，其中包括平面內11階、平面外4階。第15階模態中包含12個節點，因此在模態測試過程中至少要選擇24個測量點才能測量到前15階的所有模態振型。在本例中，選擇26個測量點，在鋼帶上均勻分布。此外在梁單元模型的振型圖上可以得知每階振型的節點的位置，在測量和激振過程中應該避開節點，以免漏掉某階模態信息。

2 模態實驗

2.1 實驗設置

模態測試采用PCB 086D80激振錘，利用Polytec OFV 353激光振動測試儀收集鋼帶表面的振動信號，并與OFV 3001控制器連接，用以調節靈敏度，避免速度信號過載。

簡化的隨行電纜為一條長2.53m的鋼帶，兩端焊接一段長0.01m的鋼絲，固定在桁架的支撐梁上，如圖1所示。鋼帶截面為矩形，寬度為0.0127m，高度為4.015×10－4m；鋼絲的直徑為1.5mm；鋼絲和鋼帶的密度為7800kg／m3，彈性模量為2.06×1011Pa；焊錫的密度為728kg／m3，彈性模量為4×109Pa。鋼帶兩端焊接的鋼絲利用夾具被固定在桁架上，固定點的水平距離與垂直距離分別為0.61m和0.60m。鋼帶被固定好以后，其平衡位置的形狀被繪在一塊平板上，以驗證有限元模型的平衡位置。

2.2 系統線性度檢查

由復模態理論可知，多自由度系統頻響函數矩陣H（ω）為對稱矩陣，即

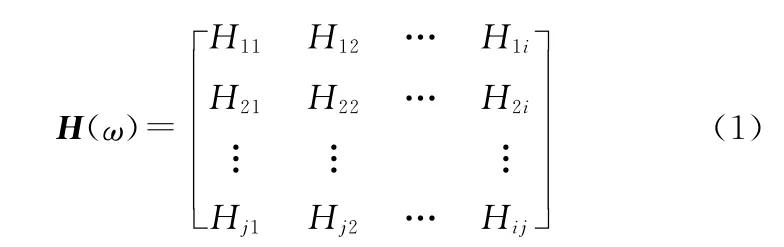
其中，Hij＝Hji，i為激振點，j為測量點。此理論表明，線性系統交換激振點和測量點的位置，其頻響函數是一致的。

為了檢驗系統線性度，對鋼帶結構進行線性度相關性實驗。在鋼帶上選取2個點，其編號為16和22，分別激發點16，測量點22，得到一條頻率范圍為0～25Hz的頻率響應函數的曲線。交換測量點和激振點，得到另一條頻率響應函數曲線，如圖2所示。兩條頻率響應函數曲線基本重合，說明系統的線性度很高。

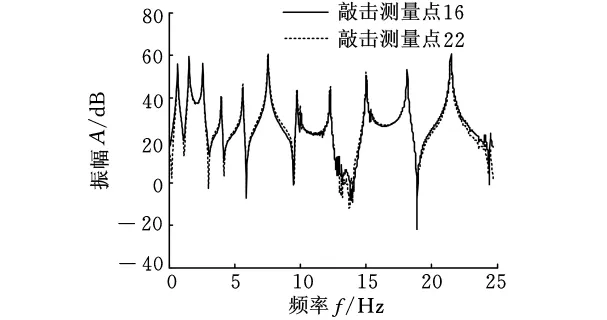
圖2 線性度相關性檢查

2.3 模態測試

由于鋼帶系統的阻尼很小，利用激振錘進行單次敲擊，其振動維持50s左右，所以決定采用單次敲擊的實驗方法。單次敲擊測量時間為32s，采樣分辨率為0.031 25Hz。平面內的振型通過26個測量點的34個頻率響應函數得到。采用移動激振錘的方法用來敲擊不同測量點，激光振動測試儀為參考點。這種方式被應用于鋼帶豎直部分的測量，即0～5和14～25測量點。如圖3a所示，在鋼帶底部環形區域，用移動激振錘的方法不能分別激發其水平和垂直方向的振動。為測試底部環形部分的水平和垂直兩個方向的振動信號，采用移動激光傳感器，激振錘作為參考點的方法進行測量，如圖3b所示，其測量點為6～13。為了分別測量垂直和水平方向的振動信號，在鋼帶的測量點處貼有不同方向的反光片。對于平面外的模態測試，即z方向的模態測試，采用移動激振錘，激光振動儀作為參考點的方式進行測量。兩個參考點分別為8和16。

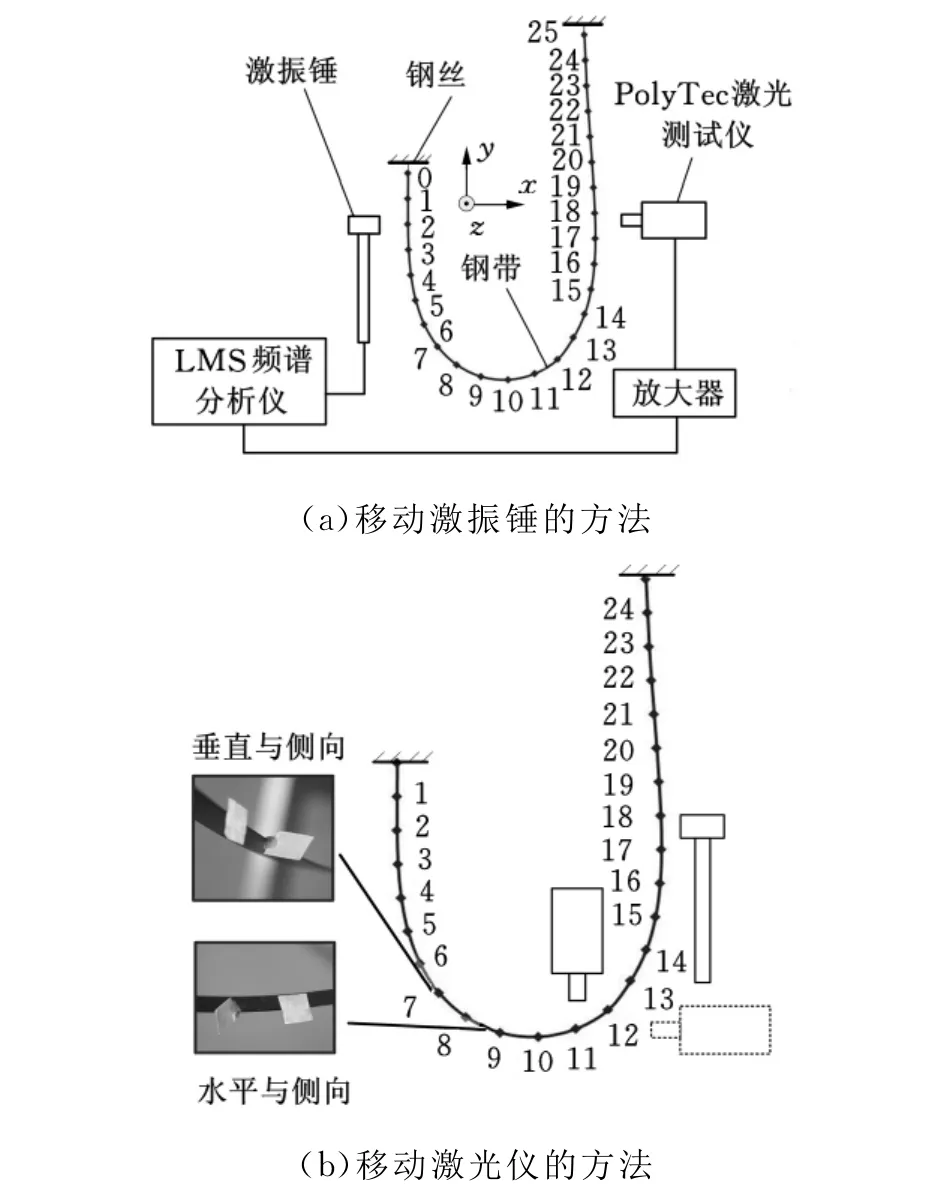
圖3 實驗方法示意圖

由于系統的線性特性，交換激振點與測量點所得到的頻率響應函數在理論上是一致的，所以可以采用兩種方法相結合的方式來測量整個鋼帶的模態參數。模態實驗中，每次敲擊實驗采用三次平均，以確保實驗數據的可靠性。

3 有限元模型分析

本文的有限元模型為精細模型，不同于量單元的粗略有限元模型。

利用ABAQUS 6.9建立鋼帶與連接用的鋼絲和焊錫的有限元模型。鋼帶與焊錫利用殼單元模擬，鋼絲用梁單元模擬，其中的連接采用tie約束，如圖4所示。求解其固有頻率和模態振型圖分為兩個步驟：第一步為求解一個非線性靜態過程，固定細長鋼帶有限元模型的兩個端點，并施加重力對鋼帶的作用，然后將細長鋼帶右端點移動到圖5所示位置形成簡化隨行電纜的有限元模型。第二步是利用perturbation的方法來計算其固有頻率和振型。圖5為靜態平衡位置示意圖，由圖可見，有限元曲線和實驗曲線幾乎重合。

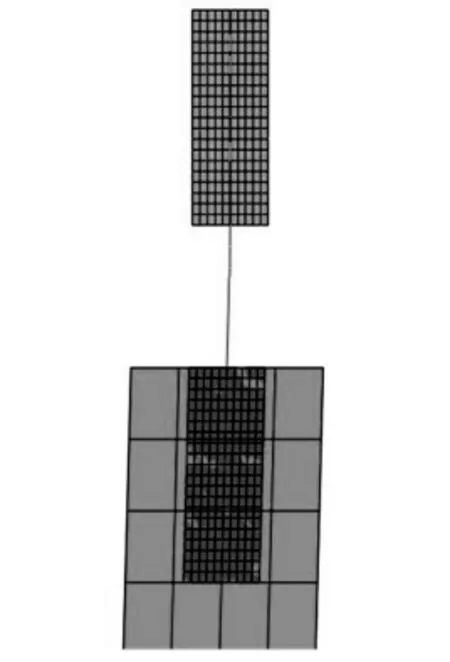
圖4 邊界條件有限元模型

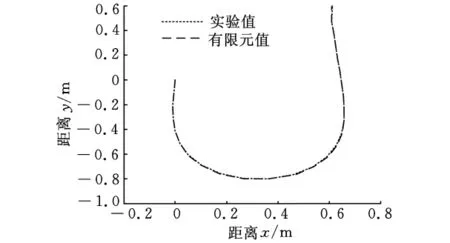
圖5 平衡位置比較

實驗和有限元得到的固有頻率如表1所示，兩者之間最大誤差不大于1.9%。模態置信度準則（modal assurance criterion）是評估實驗和分析模型振型相關程度的常用評價指標。在有限元模型中取出與實驗中測量點的位置對應的振型參數，其計算方法如下：

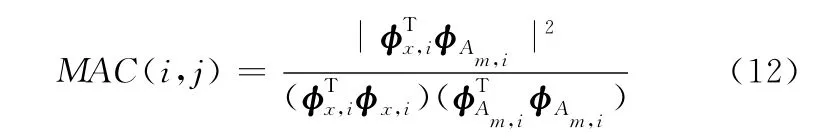
其中，φxT，i為第i階實驗得到振型參數，φAm，i是第j階有限元模型的振型參數。經計算，平面內所有的模態置信準則不低于90%，平面外不低于85%。

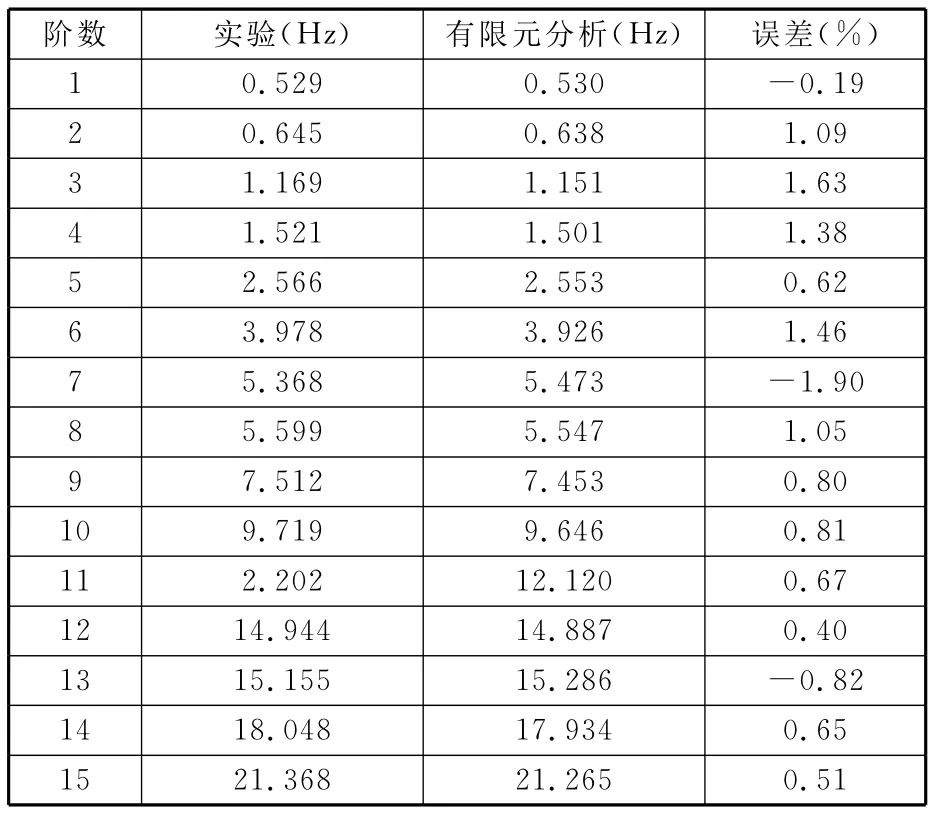
表1 實驗與有限元分析固有頻率比較

有限元分析與實驗得到的振型圖如圖6和圖7所示。其中第2階、第5階、第6階和第15階為平面內的模態，第1階、第3階、第7階和第12階為平面外的模態。由圖6可見，第2階、第5階和第6階模態處在低頻區域，而這三階模態最有可能使電纜撞擊到電梯間墻壁。更高階的平面內的模態形式類似于第15階模態。

由圖7可見，平面外第1階和第7階模態產生橫擺和彎曲運動，容易造成電纜在平面外的方向上撞擊電梯間墻壁。而第3階與第12階模態容易使隨行電纜產生打結、纏繞的趨勢。一旦電梯系統的振動頻率或者建筑物的搖擺頻率與這些頻率相近時，便可能產生“撞墻”和“打結”的現象。由此可見，三維有限元模型能夠更加全面地描述隨行電纜的動態特性。

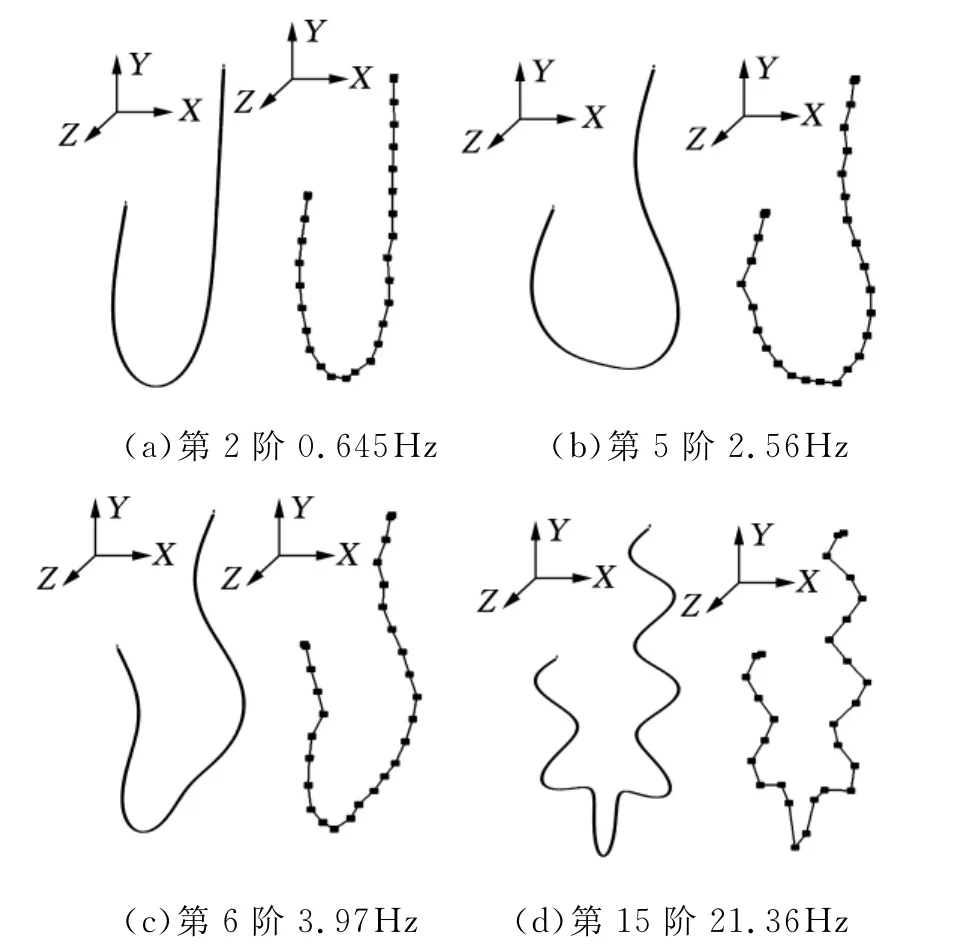
圖6 平面內的模態

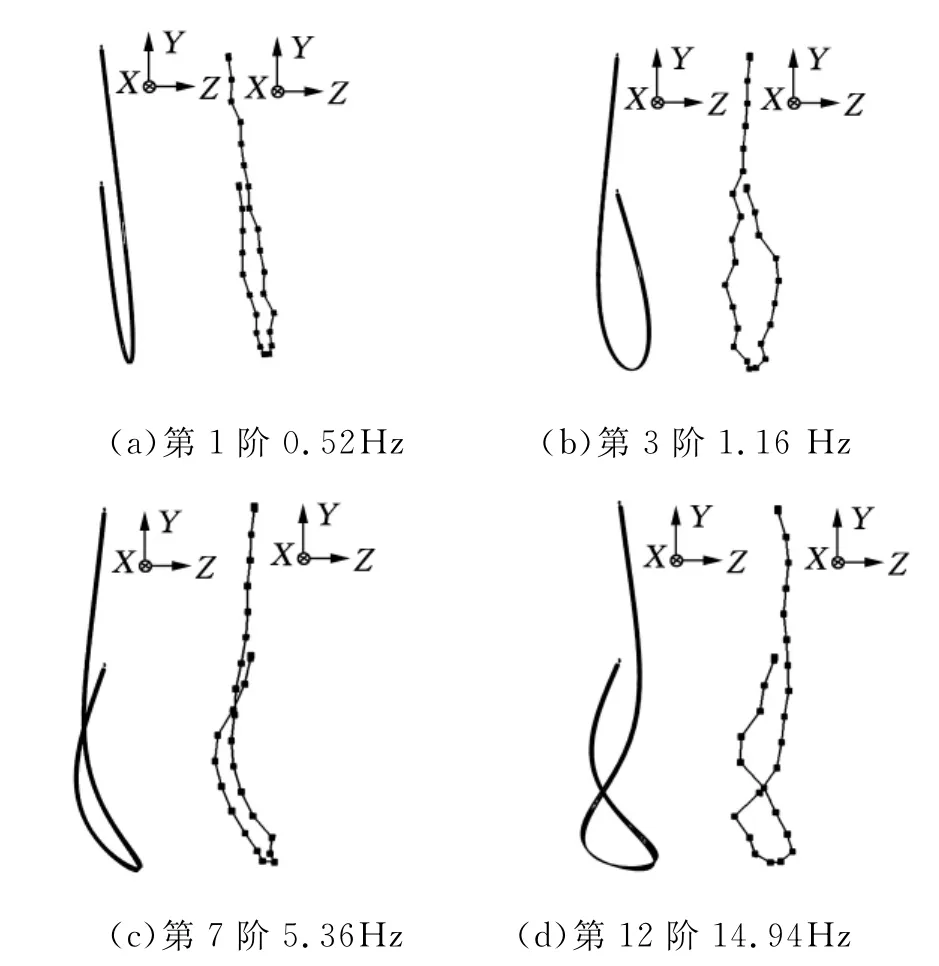
圖7 平面外的模態

本文從電梯轎廂上下運動過程中的隨行電纜的某一位置分析其動態特性。當電梯轎廂運行到不同位置時，隨行電纜的固定端與運動端的相對位置也會相應變化，不同狀態下的隨行電纜其模態參數也是不同的。為了避免由于建筑物本身的搖晃，使轎廂運動過程中的激振頻率與隨行電纜的固有頻率（特別是“擊打墻壁”與“打結”的模態頻率）相近，設計過程中應該校驗隨行電纜不同位置的固有頻率和振型。

以矩形截面的隨行電纜為例，為了能夠在設計階段就避讓共振頻率，定性分析幾何參數的變化對較敏感模態頻率的影響，見表2。

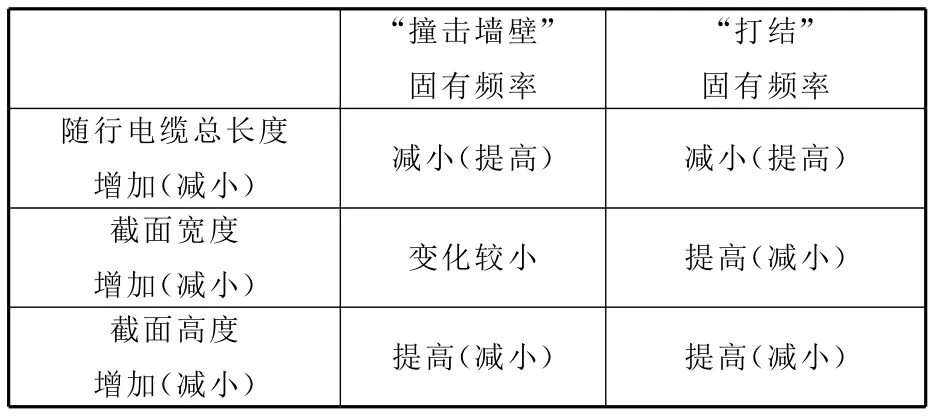
表2 幾何參數對固有頻率的影響

也可以采取以下措施來改善隨行電纜的動態特性：優化隨行電纜的總長度及固定在墻體上的高度位置；改變邊界條件，這種方式對于較短的電纜有效，但對于超長隨行電纜其效果不顯著；端部增加阻尼器衰減振動；優化電纜截面形狀、布線方式及材料，用以改變平面內和平面外的彎曲剛度。

4 結束語

本文利用殼單元和梁單元建立了簡化隨行電纜的三維有限元模型，采用移動激振錘和移動激光測振儀相結合的方式進行了模態實驗，模型計算結果和實驗結果一致，驗證了有限元模型的可靠性，指出了三維有限元模型能夠更全面描述隨行電纜的動力學特性。由模態振型圖分析了隨行電纜撞擊墻壁及打結或纏繞現象，指出隨行電纜的敏感共振頻率應該避開電梯系統振動和建筑物自身搖擺的激振頻率，并提出了改善其動力學特性的方法。

［1]Leonard J W.Nonlinear Dynamics of Cables with Low Initial Tension［J］.Journal of the Engineering Mechanics Division，1972，98（2）：293－309.

［2]Howell C T.Numerical Analysis of 2－D Nonlinear Cable Equations with Applications to Low－tension Problems［J］.International Journal of Offshore and Polar Engineering，1992，2（2）：1053－1058.

［3]Sun Y，Leonard J W.Dynamics of Ocean Cables with Local Low－tension Regions［J］.Ocean Engineering，1998，25（6）：443－463.

［4]Zhu W D，Ren H，Xiao C.A Nonlinear Model of a Slack Cable with Bending Stiffness and Moving Ends with Application to Elevator Traveling and Compensation Cables［J］.Journal of Application Mechanics，2011，78（4）：245－258.

［5]Virgin L.Effect of Weight on the Experimental Modal Analysis of Slender Cantilever Beams［C］／／ASME 2009International Design Engineering Techni－cal Conferences ＆Computers and Information in Engineering Conference.San Diego：ASME，2009：557－560.

［6]金棟平，文浩，胡海巖.繩索系統的建模、動力學和控制［J］.力學進展，2004，34（3）：304－313.

［7]邱明，廖振強，焦衛東，等.基于剛柔耦合的高方平篩動力學建模與振動模態分析［J］.中國機械工程，2008，19（24）：2960－2964.