低滲透油藏水力壓裂井應力場轉向定量評價

孫峰，李行船，熊廷松，張文豪

（1.中國石油大學（華東）儲運與建筑工程學院，山東 青島 266580；2.中國石化國際石油勘探開發有限公司，北京 100083；3.中國石油青海油田公司鉆采工藝研究院，甘肅 敦煌 736202；4.中國石化中原油田分公司采油工程技術研究院，河南 濮陽 457001）

低滲透油藏水力壓裂井應力場轉向定量評價

孫峰1，李行船2，熊廷松3，張文豪4

（1.中國石油大學（華東）儲運與建筑工程學院，山東 青島 266580；2.中國石化國際石油勘探開發有限公司，北京 100083；3.中國石油青海油田公司鉆采工藝研究院，甘肅 敦煌 736202；4.中國石化中原油田分公司采油工程技術研究院，河南 濮陽 457001）

基于多孔介質流-固耦合理論和有效應力定律，建立了孔隙壓力與地應力相互作用的低滲透油藏水力壓裂井應力場轉向評價模型，采用有限元數值模擬技術并開發相應程序對耦合模型進行求解，定量分析了低滲透油藏開發過程中水力裂縫附近區域地應力場的變化特征。計算結果表明：水力裂縫導致近裂縫區域地應力場分布特征大幅度改變，沿裂縫與垂直裂縫方向應力場大小變化各向異性，應力場轉向范圍隨初始水力裂縫長度增加而動態變化。

低滲透油藏；水力壓裂；流-固耦合；地應力場轉向；有限元數值模擬

低滲透油藏壓裂開發過程中，由于高導流能力支撐裂縫影響，孔隙壓力在裂縫周圍呈橢圓形分布，沿水力裂縫方向的流體壓力梯度變化遠大于垂直裂縫方向，致使井筒和水力裂縫附近區域地應力場大小及方向發生大幅度改變［1-4］。綜合考慮流體滲流與地應力變化之間的耦合作用，定量評價水力裂縫對地應力場分布格局的影響，對于當前低滲透油藏開發及重復壓裂改造具有重要的指導作用［5-9］。本文在考慮低滲油藏水力壓裂井近裂縫區域孔隙壓力與地應力耦合作用［10-13］的基礎上，建立了應力場轉向評價模型，采用Galerkin有限元順序解耦和參數迭代的方法求解耦合方程，應用裂縫單元處理水力裂縫與儲層區域離散的網格尺度協調問題，定量模擬了水力裂縫附近區域地應力場的變化特征。

1 耦合模型方程

地應力場轉向定量評價模型包括儲層平衡方程和流體滲流方程。假設油藏為線彈性、均質連續、多孔介質系統，由儲層骨架、孔隙流體2部分組成，孔隙介質中的流體運動符合達西定律。

1.1 儲層平衡方程

影響儲層平衡的地應力作用包括儲層骨架有效應力和流體孔隙壓力，其中骨架有效應力直接影響儲層的受力變形。

儲層骨架所受地應力、有效應力及流體孔隙壓力之間的關系可表示為

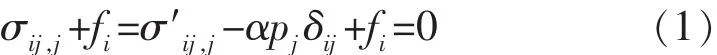
式中：σ，σ′分別為儲層骨架所受地應力、有效應力，Pa；p為流體孔隙壓力，Pa；α為 Biot系數；δ為Kronecker符號；f為體力，N/m3；i，j取值為1，2，3，代表空間的3個方向；j重復出現2次，表示該項在該指標的取值范圍內遍歷求和。

1.2 儲層流體滲流方程

基于多孔介質流-固耦合理論，儲層骨架變形影響流體壓力的分布，耦合形式的單相飽和流體連續性方程為［14］

式中：ρf為流體密度，kg/m3；φ為孔隙度；εV為骨架體積應變；t為時間，s；K為滲透率，μm2；μ為流體黏度，Pa· s；q為源匯項，kg/（m3·s）。

式（1）、式（2）構成了低滲透油藏地應力場評價耦合模型的控制方程，但均為非線性的偏微分方程，且相互影響，難以求解。

1.3 耦合方程有限元公式

本文采用Galerkin有限元方法，在上述方程基礎上引入“虛位移”，推導了耦合方程對應的等效弱積分方程。

對式（1）引入“虛位移”δu，考慮邊界高斯積分變化，得到對應的等效弱積分形式為

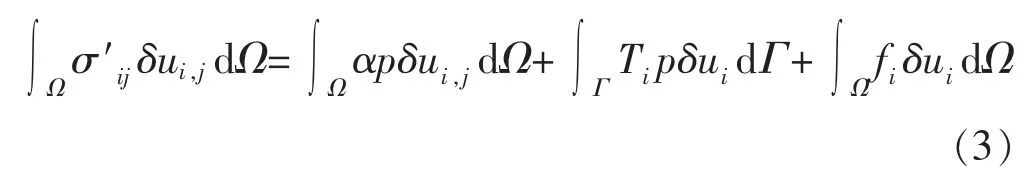
式中：Ω為求解區域；Γ為求解邊界；T為邊界力。

儲層變形平衡的Galerkin有限元公式為

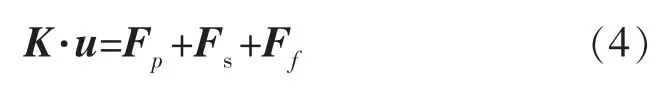
式中：K為方程剛度矩陣；u為方程變形矩陣；Fp，Fs，Ff分別為流體壓力載荷、邊界載荷和體積力載荷矩陣。

若考慮流體的微可壓縮性，應用虛位移變分原理，可得式（2）的等效弱積分形式為

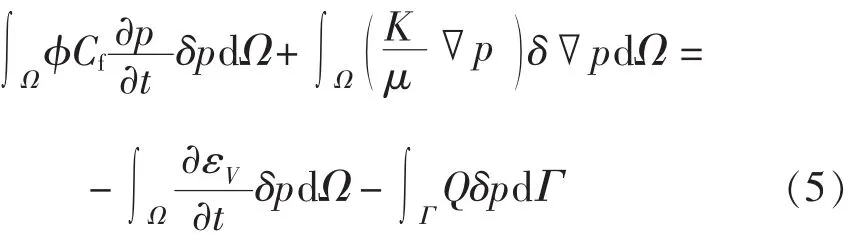
油藏流體滲流Galerkin有限元公式為

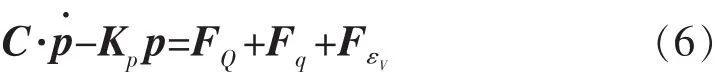
2 地應力場轉向有限元模型

2.1 模型建立

采用上述流-固耦合模型，定量分析了在某低滲透油藏的壓裂開發過程中，近裂縫區域內儲層沿裂縫方向與垂直裂縫方向上應力差值及最大水平主應力方向的變化規律。

儲層巖體物性參數為：彈性模量1.85×104MPa，泊松比0.25，孔隙度17.9%，最大、最小水平地應力分別為56.3，54.8 MPa，滲透率1.5×10-3μm2。儲層流體物性參數為：流體黏度2.55 mPa·s，孔隙壓力35 MPa，井底流壓 20 MPa，Biot系數 0.85，裂縫導流能力 10 μm2·cm。

將水力壓裂后形成的裂縫假設為理想翼對稱裂縫，考慮結構的對稱性，取計算單元的1/4部分建立有限元分析模型，并將井眼簡化成一點，如圖1所示。

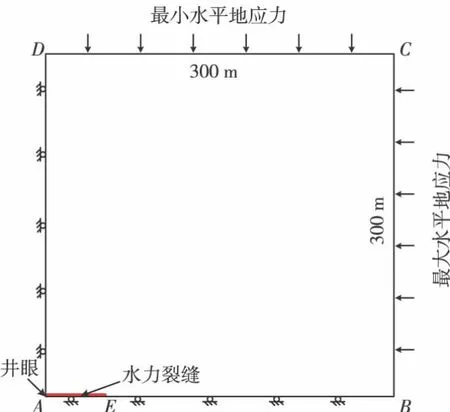
圖1 有限元計算模型

2.2 耦合模型求解程序設計

在模型求解過程中，將程序劃分為地應力和流體滲流2個計算模塊，模塊中有限元網格節點一一對應。地應力模塊邊界條件如圖1所示，BC，CD邊分別施加最大、最小水平地應力，AB，AD邊分別施加位移約束條件。流體滲流模塊中，在井眼A處施加井底流壓條件，BC，CD為施加儲層流體壓力邊界，AB，AD為流量封閉邊界。

對于全耦合形式的有限元公式（4）和（6），采用儲層變形—流體滲流順序解耦的方法求解，用上一時間步的儲層應力、應變迭代求解油藏的流體壓力，通過耦合項數據循環迭代傳遞實現求解。

計算中將水力裂縫AE段處理為一維高導流裂縫桿單元［15］，將桿單元的質量、剛度矩陣變化疊加到連續儲層單元的有限元方程項中，形成儲層-裂縫組合單元模型，解決模擬分析中儲層、裂縫網格尺度匹配問題。

3 結果分析

3.1 應力差值變化

井眼A處建立生產壓差后，由于裂縫的高導流能力，沿裂縫方向的儲層流體壓力梯度變化遠大于垂直裂縫方向，導致近裂縫區域儲層沿裂縫方向的有效應力下降幅度大于垂直裂縫方向，應力場的方向發生偏轉。隨著孔隙壓力的擴散傳播，儲層不同位置處，沿裂縫與垂直裂縫方向的應力差隨時間增加而改變。

對應裂縫長度Lf為50 m、生產壓差為15 MPa工況下，沿裂縫與垂直裂縫方向的應力差值變化見圖2。由圖2可以看出：

1）等值線數值小于0時，表明該區域內沿裂縫方向地應力小于垂直裂縫方向，最大水平主應力方向發生偏轉。

2）數值為0的等值線為應力各向同性線，與沿井眼垂直裂縫方向交點處為應力各向同性點。模擬結果中，t為10，30 d時，應力差的應力各向同性點距井眼分別為9.7，14.3 m。

3）等值線數值大于0時，表明該區域內沿裂縫方向地應力大于垂直方向，應力場方向未發生偏轉。

4）模擬工況下，水力裂縫附近發生應力場轉向的區域范圍隨生產時間的增加而擴展。

3.2 最大水平主應力方向

Lf=50 m的近裂縫壁區域內，儲層最大水平主應力場方向分布格局變化見圖3。近裂縫區域最大水平主應力方向發生90°偏轉，垂直井眼方向最大轉向距離達到12.8 m。隨著距裂縫距離的增大，儲層流體壓力梯度變化減小，最大水平主應力方向仍為水平方向。

Lf=100 m時最大水平主應力方向分布格局見圖4。與儲層有效應力大小變化對應，模擬裂縫長度100 m工況下最大水平主應力沿垂直裂縫方向發生偏轉的距離增大，發生90°偏轉的最大距離達到17.5 m。

計算結果表明：隨裂縫長度增加，壓力梯度沿裂縫方向的變化范圍進一步擴展，最大水平主應力方向發生轉向的范圍增大。

圖2 水力裂縫導致的應力差值變化

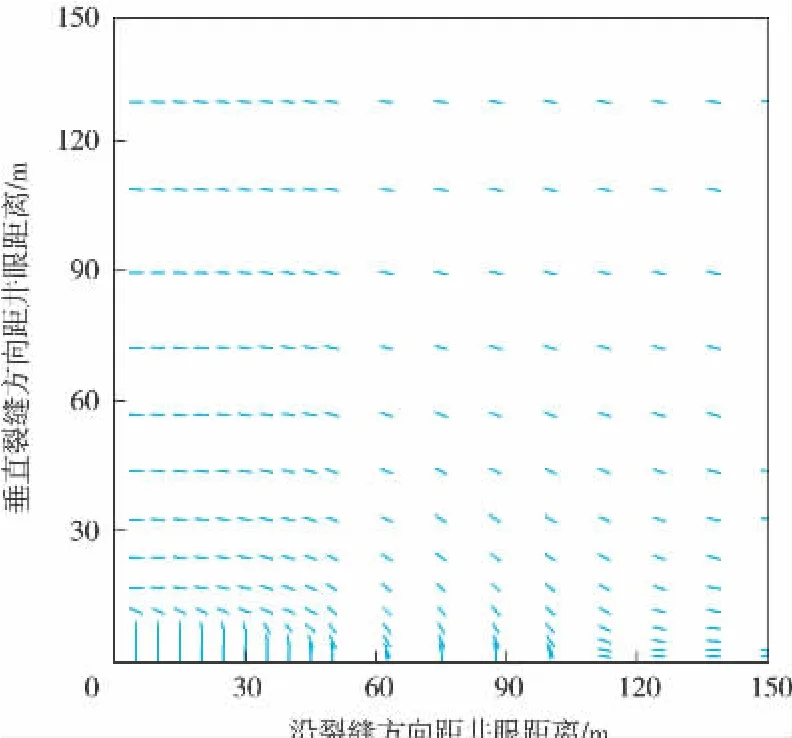
圖3 Lf=50 m時最大水平主應力方向分布

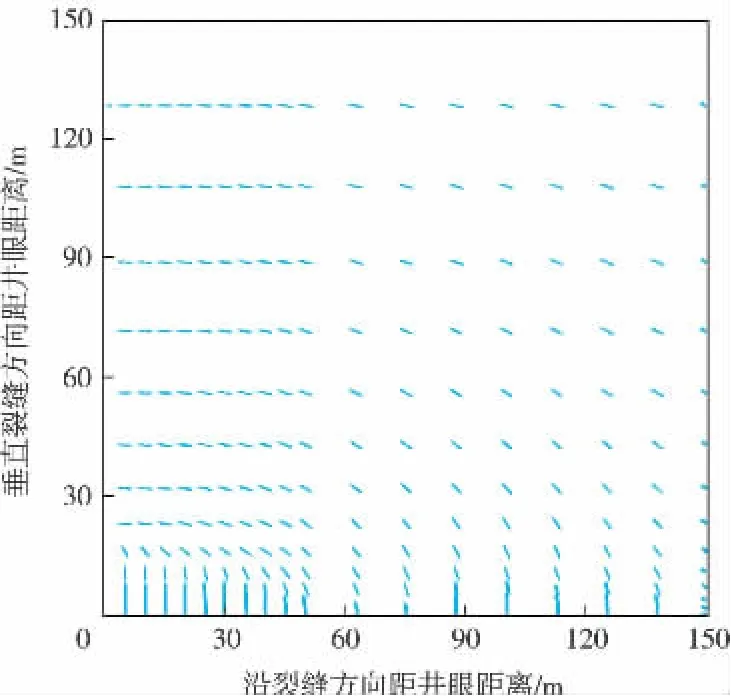
圖4 Lf=100 m時最大水平主應力方向分布

4 結論

1）基于多孔介質流-固耦合理論和有效應力定律，建立了孔隙壓力與地應力相互作用的低滲透油藏水力壓裂井應力場轉向評價模型，推導了模型對應的Galerkin有限元公式，采用順序解耦和參數迭代的方法求解耦合方程。

2）由于裂縫的高導流能力，沿裂縫方向儲層流體的壓力梯度變化遠大于垂直裂縫方向，導致近裂縫區域儲層水平方向的有效應力下降大于垂直方向，最大水平主應力方向發生偏轉，轉向范圍隨初始裂縫長度增加而增大。

［1］ Siebrits E，Elbel J L，Detoumay E，et al.Parameters affecting azimuth and length of a secondary fracture during a refracture treatment［R］. SPE 48928，1998.

［2］ Siebrits E，Elbel J L，Hoover R S，et al.Refracture reorientation enhances gas production in Barnett shale tight gas wells［R］.SPE 63030，2000.

［3］ 劉洪，胡永全，趙金洲，等.重復壓裂氣井誘導應力場模擬研究［J］.巖石力學與工程學報，2004，23（23）：4022-4027.

［4］ 張廣清，陳勉，姚飛，等.各向異性地層重復壓裂最優化時機及影響因素分析［J］.石油學報，2008，29（6）：885-888.

［5］ 勞斌斌，劉月田，屈亞光，等.水力壓裂影響因素的分析與優化［J］.斷塊油氣田，2010，17（2）：225-228.

［6］ 艾敬旭，單學軍，侯天江.五點井網注水井壓裂裂縫參數對油井產量的影響［J］.斷塊油氣田，2011，18（5）：649-652.

［7］ 吳超，劉建華.區域油田地應力及井壁穩定性綜合預測方法［J］.斷塊油氣田，2011，18（6）：705-709.

［8］ Aghighi M A，Ramhman S S，Rahman M M.Effect of formation stress distribution on hydraulic fracture reorientation in tight gas sands［R］. SPE 122723，2009.

［9］ Zhai Z Y，Sharma M M.Estimating fracture reorientation due to fluid injection/production［R］.SPE 106387，2007.

［10］劉建軍，劉先貴，胡雅礽，等.低滲透儲層流-固耦合滲流規律的研究［J］.巖石力學與工程學報，2002，21（1）：88-92.

［11］徐軒，楊正明，祖立凱，等.多重介質儲層滲流的等效連續介質模型及數值模擬［J］.斷塊油氣田，2010，17（6）：733-737.

［12］張廣明，熊春明，劉合，等.復雜斷塊地應力場數值模擬方法研究［J］.斷塊油氣田，2011，18（6）：710-713.

［13］Settari A，Walters D A.Advances in coupled geomechanical and reservoir modeling with applications to reservoir compaction［R］.SPE 51927，1999.

［14］Fung L S K.A coupled geomechanic multiphase flow model for analysis of in-situ recovery in cohesionless oil sands［J］.JCPT，1992，31（6）：56-67.

［15］孫峰，薛世峰，仝興華，等.介質變形對低滲透油藏壓裂產能影響有限元模擬［J］.石油學報，2010，31（5）：820-824.

（編輯 孫薇）

Quantitative evaluation on stress redistribution for hydraulic fracturing well of low-permeability reservoir

Sun Feng1,Li Xingchuan2,Xiong Tingsong3,Zhang Wenhao4
(1.College of Storage&Transportation and Civil Engineering,China University of Petroleum,Qingdao 266580,China;2.International Petroleum Exploration and Production Corporation,SINOPEC,Beijing 100083,China;3.Drilling and Production Technology Institute,Qinghai Oilfield Company,PetroChina,Dunhuang 736202,China;4.Research Institute of Oil Production Engineering Technology,Zhongyuan Oilfield Company,SINOPEC,Puyang 457001,China)

An evaluation model of stress redistribution for hydraulic fracturing well of low-permeability reservoir with the interaction of pore pressure and stress was established on the basis of fluid-solid coupling theory and effective stress principle for porous media. Coupled model was solved through the adaptation of finite element simulation and the development of relevant programme.The change feature of stress field around hydraulic fracture was quantitatively evaluated during the development of low-permeability reservoir.The computed results indicated that hydraulic fracture created the stress redistribution near fracture area was greatly changed,and that the size change of stress field showed the anisotropy along the fracture and vertical fracture direction and the area of stress redistribution was a function of initial hydraulic fracture length.

low-permeability reservoir;hydraulic fracturing;fluid-solid coupling;stress redistribution;finite element simulation

中國石油重大科技專項“低滲敏感儲層滲流機理及增注技術研究”（2012-ZG-009）

TE319

A

10.6056/dkyqt201204020

2012-02-01；改回日期：2012-05-19。

孫峰，男，1979年生，講師，博士，2010年畢業于中國石油大學（華東）地質資源與地質工程專業，現主要從事油氣田地下工程力學研究。E-mail：hdpusf@163.com。

孫峰，李行船，熊廷松，等.低滲透油藏水力壓裂井應力場轉向定量評價［J］.斷塊油氣田，2012，19（4）：489-492.

Sun Feng，Li Xingchuan，Xiong Tingsong，et al.Quantitative evaluation on stress redistribution for hydraulic fracturing well of low-permeability reservoir［J］.Fault-Block Oil&Gas Field，2012，19（4）：489-492.